Способ изменения наклонения и высоты орбиты космического летательного аппарата с использованием границ области малой устойчивости
Формула / Реферат
1. Способ изменения, по меньшей мере, наклонения и высоты космического летательного аппарата в зоне притяжения, по меньшей мере, двух небесных тел, включающий следующие независимые стадии:
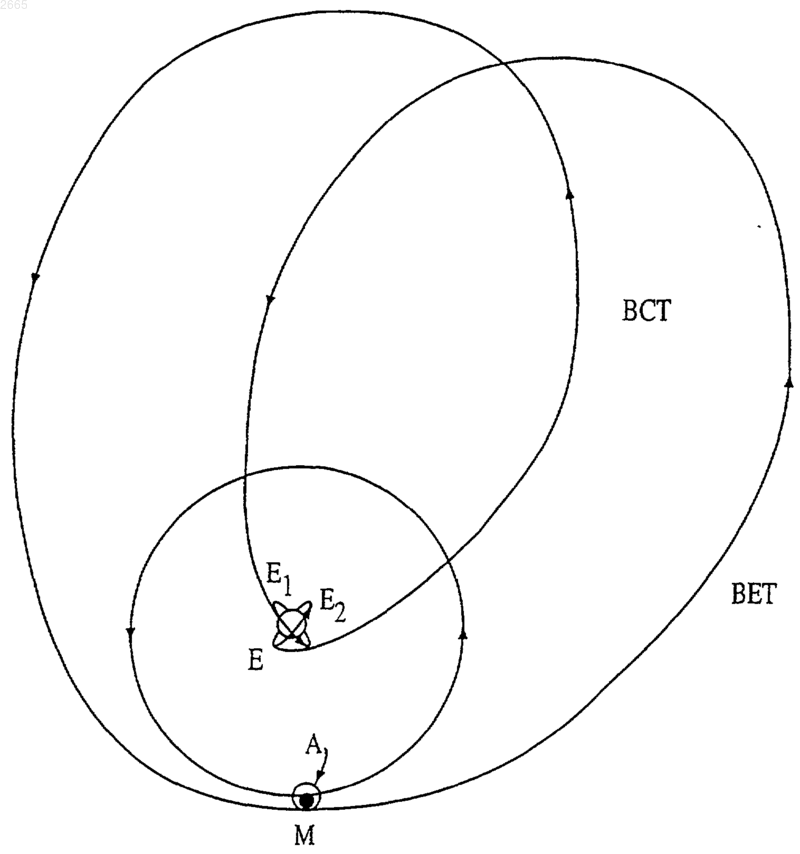
а) осуществление перехода летательного аппарата с его орбиты относительно первого небесного тела или с поверхности первого небесного тела до обеспечения слабого захвата в области слабой устойчивости (WSB) или на орбите в области (WSB), связанной с первым и вторым небесными телами,
б) проведение опционно в области WSB или на орбите в области WSB, по меньшей мере, одного маневра летательным аппаратом посредством изменения его скорости с обеспечением схода его с орбиты в области WSB,
в) осуществление второго перехода летательного аппарата от области WSB или схода его с орбиты в области WSB, по меньшей мере, ко второму небесному телу, либо на орбиту ко второму небесному телу, либо на другую орбиту к первому небесному телу.
2. Способ по п.1, отличающийся тем, что первый переход предусматривает использование, по меньшей мере, операционного баллистического захвата (ВСТ) и хомановского перехода.
3. Способ по п.1 или 2, отличающийся тем, что второй переход предусматривает использование, по меньшей мере, операционного баллистического схода с орбиты (BET) и хомановского перехода.
4. Способ по пп.1-3, отличающийся тем, что первый переход предусматривает использование операционного баллистического захвата (ВСТ), причем операция перемещения (а) дополнительно включает в себя операцию перелета с использованием захвата (ВСТ) от первого небесного тела или с орбиты первого небесного тела, до обеспечения слабого захвата в указанной области слабой устойчивости (WSB) или на орбите в указанной области (WSB), связанной с первым небесным телом, за счет внедрения процесса позиционирования вперед путем изменения параметров до обеспечения сходимости заданных переменных в области (WSB) или на орбите в области (WSB).
5. Способ по пп.1-3, отличающийся тем, что первый переход предусматривает использование операционного баллистического захвата (ВСТ), причем операция перемещения (а) дополнительно включает в себя операцию перелета с использованием захвата (ВСТ) от первого небесного тела или с орбиты первого небесного тела до обеспечения слабого захвата в области слабой устойчивости (WSB) или на орбите в указанной области (WSB), связанной с первым небесным телом, за счет внедрения процесса позиционирования вперед путем изменения, по меньшей мере, двух сферических параметров, до обеспечения сходимости заданных переменных в области (WSB) или на орбите в области (WSB) при сохранении, главным образом, фиксированной, по меньшей мере, одной классической переменной, использованной в процессе позиционирования вперед.
6. Способ по пп.1-3, отличающийся тем, что первый переход предусматривает использование операционного баллистического захвата (ВСТ), причем операция перемещения (а) дополнительно включает в себя операцию перелета с использованием захвата (ВСТ) от первого небесного тела или с орбиты первого небесного тела до обеспечения слабого захвата в области слабой устойчивости (WSB) или на орбите в указанной области (WSB), связанной с первым небесным телом, за счет внедрения процесса позиционирования вперед путем изменения значения скорости VE и угла наклона траектории полета gE для обеспечения сходимости заданных переменных в указанной области (WSB) или на орбите в области (WSB), причем заданные переменные включают в себя радиальное расстояние rM и наклонение iM.
7. Способ по пп.1-3, отличающийся тем, что первый переход предусматривает использование операционного баллистического захвата (ВСТ), причем операция перемещения (а) дополнительно включает в себя операцию перелета с использованием первого перехода от первого небесного тела или с орбиты первого небесного тела до обеспечения слабого захвата в области слабой устойчивости (WSB) или на орбите в указанной области (WSB), связанной с первым небесным телом, за счет внедрения процесса позиционирования вперед, который включает в себя ньютоновский алгоритм второго порядка, причем в ньютоновском алгоритме второго порядка используют две переменные управления, включающие в себя значение скорости VE и угол наклона траектории полета gE, которые изменяют для достижения условий указанной области (WSB) у второго небесного тела или на орбите второго небесного тела, с использованием двух заданных переменных, в том числе радиального расстояния rM и наклонения iM.
8. Способ по п.7, отличающийся тем, что значение скорости VE и угол наклона траектории полета gE развязаны от второго небесного тела или от орбиты второго небесного тела при первом переходе.
9. Способ по п.7, отличающийся тем, что значение скорости VE и угол наклона траектории полета gE развязаны от угловых элементов первого небесного тела, в том числе от наклонения iE, восходящего узла относительно Земли WE и аргумента периапсиды относительно первого небесного тела wE.
10. Способ по одному из пп.1-9, отличающийся тем, что операция (b) дополнительно включает в себя проведение маневра с параметрами 2-20 м/с в указанной области (WSB) или на орбите в области (WSB) для выхода из указанной области или для схода с орбиты.
11. Способ по одному из пп.1-10, отличающийся тем, что операция (а) дополнительно включает в себя проведение маневра вокруг второго небесного тела или на орбите второго небесного тела за счет проведения другого маневра с параметрами 2-20 м/с в области (WSB) или на орбите в области (WSB).
12. Способ по одному из пп.1-11, отличающийся тем, что указанная область (WSB) или орбита в указанной области (WSB) являются нелинейными и находятся, главным образом, на границе захвата и ухода, в результате чего возможен как захват, так и уход при, главным образом, нулевом или относительно малом маневре, причем гравитационные возмущения солнца оказывают воздействие как на первый, так и на второй переходы.
13. Способ по одному из пп.1-12, отличающийся тем, что указанная область (WSB) или орбита в указанной области (WSB) находятся главным образом на границе взаимодействия между гравитационными полями первого небесного тела и второго небесного тела.
14. Способ по одному из пп.1-13, отличающийся тем, что, по меньшей мере, космический корабль, спутник или ракета входят, по меньшей мере, в указанную область (WSB) или переходят на орбиту в области (WSB) таким образом, что кеплеровская энергия, по меньшей мере, космического корабля, спутника или ракеты является слегка отрицательной близкой к нулю.
15. Способ по одному из пп.1-14, отличающийся тем, что, по меньшей мере, только указанная область (WSB) или орбита в указанной области (WSB) реализованы на заранее определенной случайной высоте путем задания заранее определенного значения скорости, по меньшей мере, космического корабля, спутника или ракеты, в результате чего определен заданный эксцентриситет захвата.
16. Способ по одному из пп.1-15, отличающийся тем, что операция (а) дополнительно включает в себя проведение маневра вокруг второго небесного тела или на орбите второго небесного тела за счет проведения другого маневра с параметрами 2-20 м/с в указанной области (WSB) или на орбите в указанной области (WSB), по меньшей мере, только при синхронизации и при позиционировании, по меньшей мере, космического корабля, спутника или ракеты ранее выхода из указанной области (WSB) или схода с орбиты в указанной области (WSB).
17. Способ по одному из пп.1-16, отличающийся тем, что второй переход предусматривает использование операционного баллистического схода с орбиты (BET), причем операция перемещения (с) дополнительно включает в себя перелет с использованием схода с орбиты (ВСТ) от состояния слабого захвата в области слабой устойчивости (WSB) или на орбите в указанэющ области (WSB), по меньшей мере, только к первому небесному телу, или на орбиту первого небесного тела, или ко второму небесному телу, или на орбиту второго небесного тела за счет внедрения процесса позиционирования вперед путем изменения вторых параметров способа до обеспечения сходимости вторых заданных параметров в указанной области (WSB) или на орбите в указанной области (WSB).
18. Способ по п.17, отличающийся тем, что вторые заданные переменные развязаны, по меньшей мере, от первого небесного тела или от орбиты первого небесного тела и от угловых элементов второго небесного тела.
19. Способ по одному из пп.1-18, отличающийся тем, что в качестве первого небесного тела или орбиты первого небесного тела используют Землю или околоземную орбиту, а в качестве второго небесного тела или орбиты второго небесного тела используют Луну или окололунную орбиту.
20. Способ по п.1, отличающийся тем, что для обеспечения перехода космического летательного аппарата от первого небесного тела или с орбиты первого небесного объекта ко второму небесному телу или на орбиту второго небесного тела осуществляют независимые стадии
(a) ввода параметров способа генерирования операционного баллистического захвата для перехода;
(b) осуществления процесса позиционирования вперед, изменяя при этом параметры для сходимости заданных переменных второго небесного тела или на орбите второго небесного тела от первого небесного тела или от орбиты первого небесного тела; и
(c) повторения стадии (b) до достижения достаточной сходимости, получение операционного баллистического захвата для перехода от первого небесного тела или орбиты первого небесного тела ко второму небесному телу или на орбиту второго небесного тела.
21. Способ по п.20, отличающийся тем, что стадия повторения (с) дополнительно включает стадию повторения (b) до достижения достаточной сходимости, чтобы получить операционный баллистический захват для перехода от первого небесного тела или сходя с орбиты первого небесного тела ко второму небесному телу или на орбиту второго небесного тела через область слабой устойчивости (WSB) на орбите между ними.
22. Способ по п.20 или 21, отличающийся тем, что стадия осуществления процесса (b) дополнительно включает стадию внедрения процесса позиционирования вперед, изменяя, по меньшей мере, два сферических параметра для сходимости заданных переменных у второго небесного тела или на орбите второго небесного тела при поддержании постоянства, по меньшей мере, одной классической переменной, используемой в указанном процессе позиционирования вперед.
23. Способ по п.20 или 21, отличающийся тем, что стадия осуществления процесса (b) дополнительно включает стадию процесса позиционирования вперед при изменении величины скорости VE и угла наклона траектории полета gE для сходимости заданных переменных у второго небесного тела или на орбите второго небесного тела, причем заданные переменные включают радиальное расстояние rM и наклонение iM.
24. Способ по п.20 или 21, отличающийся тем, что стадия осуществления процесса (b) дополнительно включает стадию процесса позиционирования вперед, включающую ньютоновский алгоритм второго порядка, причем в ньютоновском алгоритме второго порядка используют две переменные управления, включая величину скорости VE и угол наклона траектории полета gE, которые изменяют для достижения условий захвата у второго небесного тела или на орбите второго небесного тела, используя две заданные переменные, включая радиальное расстояние rM и наклонение iM.
25. Способ по п.23 или 24, отличающийся тем, что величина скорости VE и угол наклона траектории полета gE развязаны от второго небесного тела или от орбиты второго небесного тела при осуществлении операционного баллистического захвата для перехода.
26. Способ по п.23 или 24, отличающийся тем, что величина скорости VE и угол наклона траектории полета gE развязаны от угловых элементов первого небесного тела, в том числе от наклонения iE, восходящего узла относительно Земли WE и аргумента периапсиды относительно первого небесного тела wE.
27. Способ по любому из пп.20 или 26, отличающийся тем, что стадия процесса (b) дополнительно включает стадию генерирования траектории вокруг второго небесного тела или орбиты второго небесного тела, включая выполнение незначительного маневра с параметрами 2-20 м/с в области слабой устойчивости (WSB) или на орбите (WSB), связанной со вторым небесным телом.
28. Способ по п.27, отличающийся тем, что область (WSB) или орбиту в области (WSB) определяют как нелинейную, находящуюся, в основном, на границе захвата и ухода, в результате чего возможен как захват, так и уход при существенно нулевом или относительно малом маневре, при этом гравитационные возмущения Солнца оказывают воздействие, как на первый, так и на второй переходы.
29. Способ по п.27 или 28, отличающийся тем, что область (WSB) или орбиту в указанной области (WSB) определяют, в основном, на границе взаимодействия между гравитационными полями первого небесного тела и второго небесного тела.
30. Способ по п.27, 28 или 29, отличающийся тем, что, по меньшей мере, космический корабль, спутник или ракета входят, по меньшей мере, в область (WSB) или переходят на орбиту в области (WSB) таким образом, что кеплеровская энергия, по меньшей мере, космического корабля, спутника или ракеты является слегка отрицательной и, в основном, близкой к нулю.
31. Способ по любому из пп.27-30, отличающийся тем, что, по меньшей мере, область (WSB) или орбита в указанной области (WSB) реализованы на заранее определенной случайной высоте путем задания заранее определенного значения скорости, по меньшей мере, космического корабля, спутника или ракеты, в результате чего определен заданный эксцентриситет захвата.
32. Способ по любому из пп.21-31, отличающийся тем, что стадия осуществления процесса (b) дополнительно включает стадию проведения маневра вокруг второго небесного тела или на орбите второго небесного тела за счет проведения другого маневра с параметрами 2-20 м/с в области (WSB) или на орбите в области (WSB), по меньшей мере, при синхронизации и при позиционировании, по меньшей мере, космического корабля, спутника или ракеты до выхода из области (WSB) или схода с орбиты в области (WSB).
33. Способ по любому из пп.21-32, отличающийся тем, что процесс позиционирования вперед предусматривает использование ньютоновского алгоритма второго порядка.
34. Способ по любому из пп.23-26, отличающийся тем, что дополнительно включает следующие стадии:
(d) преобразование величин сходимости VE, gE в классические элементы;
(e) преобразование классических элементов в сферические координаты, в котором сферические координаты включают преобразованные величины VE, gE, а также долготу a E, широту d E, азимут/угол траектории полета с измененной вертикалью s E.
35. Способ по любому из пп. 21-34, отличающийся тем, что в качестве первого небесного тела или орбиты первого небесного тела используют Землю или околоземную орбиту, а в качестве второго небесного тела или орбиты второго небесного тела используют Луну или окололунную орбиту.
Текст
1 Данная заявка на изобретение связана с предварительной заявкой на изобретение США серийный номер 60/041,465, поданной 25 марта 1997 г., от имени изобретателя Edward A. Belbruno, при этом указанная заявка включена в данное описание в качестве ссылки, в том числе с учетом и всех имеющихся в ней ссылок. Настоящее изобретение главным образом имеет отношение к созданию способов перемещения в космическом пространстве, а в частности, к созданию способов изменения наклонений (к плоскости экватора) объекта, выводимого на орбиту вокруг Земли, Луны и/ или других планет, такого как спутник, космический летательный аппарат, и т.п. с использованием, например, границ области малой (слабой) устойчивости (WSBs). Изучение движения объектов, в том числе космических объектов, частично восходит к механике Ньютона. В течение 18-го и 19-го столетий использование в соответствии с механикой Ньютона закона движения, описываемого(задаваемого) ускорением, обеспечивало упорядоченные и полезные рамки для разрешения большинства представляющих интерес в то время проблем небесной механики. Для задания исходного состояния ньютоновской системы должны быть заданы скорости и положения каждой частицы. Однако в середине 19-го столетия Гамильтон переработал формулирование динамических систем за счет ввода так называемой функции(оператора) Гамильтона, Н, которая отображает полную энергию системы, выраженную в терминах положения и количества движения, что представляет собой описание в виде дифференциального уравнения первого порядка. Этот гамильтоновский аспект первого порядка, который отображает универсальную математическая модель, используемую для моделирования динамических систем в физике, подразумевает детерминизм для классических систем, а также обеспечивает связь с квантовой механикой. В начале 1900-х годов Пуанкаре понял, что классическая ньютоновская проблема трех тел создает сложный динамический набор, который является весьма чувствительным в зависимости от исходных условий, что в настоящее время именуется теорией хаоса. Происхождение хаотического движения может быть прослежено назад к классической (гамильтоновской) механике, которая является основой (современной) классической физики. В частности, именно гамильтоновская неинтегрируемая механика и связанные с ней нелинейные проблемы создают дилемму и в конечном счете обеспечивают способность проникновения в суть появлении случайности и непредсказуемости в полностью детерминированных системах. Появление компьютеров создало инструмент, которого до этого так не хватало в ранее проводимых исследованиях, таких как работы 2 Пуанкаре, что исключало неинтегрируемую гамильтоновскую механику из основного потока физических исследований. Сочетание развития вычислительной методологии с глубокими интуитивными проникновениями в суть явлений в начале 1960-х годов привело к формулированию теоремы КАМ, названной так по первым буквам фамилий А.Н. Колмогорова, В.И. Арнольда и Мозера, которая обеспечивает условия анализа случайного характера и непредсказуемости для практически неинтегрируемых гамильтоновских систем. В рамках современных воззрений некоторые классы нелинейных проблем являются почти синонимичными так называемому хаотическому поведению. Хаос представляет собой не просто беспорядок, а скорее порядок без периодичности. Интересным и разоблачающим аспектом хаотического поведения является то, что оно может представляться случайным, когда генерирующие алгоритмы являются конечными,что описывается так называемыми логистическими уравнениями. Хаотическое движение является важным для решения астрофизических (орбитальных) проблем, в частности, просто потому, что очень часто в пределах главным образом хаотических областей могут быть вкраплены картины упорядоченного движения с хаотической деятельностью в меньшем масштабе. По причине взвешенных (масштабированных) характеристик ключевым элементом является достижение достаточно высокой разрешающей способности при проведении цифровых вычислений, для того, чтобы точно описать количественное поведение, которое позволяет выявлять хаотическую активность определенного рода. Такая высокая точность требуется потому, что вместо намного более знакомой пространственной или временной периодичности проявляется тип масштабной инвариантности. Указанная масштабная инвариантность, обнаруженная Фейгенбаумом(Feigenbaum) для одномерного отображения в виде карты, обеспечивает возможность рассмотрения анализирующих групп ренормализации в пределах хаотических переходных участков. Проникновение в суть стохастической механики также было обеспечено за счет соответствующего развития нелинейного анализа, такого как открытие связи между нелинейной динамикой и современной эргодической теорией. Например, если усреднения по времени вдоль траектории на потенциальном рельефе равны совокупности усреднений по всему потенциальному рельефу, то система считается эргодической на всему ее потенциальному рельефу. В случае классических систем случайность тесно связана с эргодичностью. В случае характеризующих аттракторов в диссипативных системах(в системах с рассеиванием) встречаются аналогии эргодическому поведению. 3 Примером присущего системе случайного поведения является работа Лоренца (E.N.Lorenz) по теплопроводности, в которой показано, что полностью детерминистические системы, заданные тремя обычными дифференциальными уравнениями, испытывают нерегулярные(беспорядочные) флуктуации. Такие ограниченные, непериодические события, которые являются нестабильными, могут вносить турбулентность и поэтому они могут быть названы хаосом, который имеет ассоциативную связь с выявленным случайным движением на некоторых отображениях в виде карты. Одной из проверок, которые могут быть использованы для различения хаоса от истинного случайного поведения, является оценка алгоритмической сложности; случайная последовательность нулей и единиц может быть воспроизведена только за счет копирования полной последовательности, то есть при этом периодичность не оказывает никакого содействия. Оператор Гамильтона стремится описать движение в терминах уравнений движения первого порядка. Полезность такой точки зрения заключается в обеспечении основы для теоретического расширения на различные физические модели, первыми среди которых являются объекты механики небесных тел. Гамильтоновские уравнения являются справедливыми (поддерживаются) в случае как специальной, так и общей теории относительности. Более того, в рамках классической механики они образуют основу для дальнейшего развития, такую как известный способ Гамильтона-Якоби (Hamilton-Jacobi), и,при еще большем расширении, образуют основу для методов (малых) возмущений. Этот последний аспект гамильтоновской теории обеспечивает исходную точку для аналитического обсуждения, которое будет здесь конспективно проведено. Как уже упоминалось, оператор Гамильтона главным образом стремится описать движение в терминах уравнений движения первого порядка. Движение в интегрируемой системе Гамильтона с N степенями свободы главным образом является периодическим и ограниченным N-тором, как это показано на фиг. 1. На фиг. 1 показана интегрируемая система с двумя степенями свободы на торе и с замкнутой орбитой траектории. Торы КАМ представляют собой концентрические версии единичного тора. Все системы Гамильтона с N=1 являются интегрируемыми, в то время как абсолютное большинство систем с N больше или равно 2 становится неинтегрируемыми. Интеграл движения, который дает возможность понизить порядок набора уравнений, именуется первым интегралом. Для интеграции набора дифференциальных уравнений порядка 2N,обычно требуется такое же число интегралов, за исключением случая гамильтоновских уравнений движения, когда достаточны N интегралов. 4 Это может быть также выражено в терминах теоремы Лиувиля (Liouville), в которой утверждается, что любая область фазового пространства должна оставаться постоянной при любой(интегрируемой) математической модели Гамильтона. Область фазового пространства может изменять свою форму, но не свой объем фазового пространства. Поэтому для любой консервативной динамической системы, такой как движение планет или маятника, фазовое пространство должно оставаться постоянным. Другим применением оператора Гамильтона, который рассматривался вначале как оператор для постоянного движения, является его привлечение для непостоянных и хаотических траекторий. Пуанкаре установил, что неинтегрируемые классические тройные (трехмерные,three-body) системы могут приводить к хаотическим траекториям. Хаотическое поведение не вызвано ни большим числом степеней свободы,ни любой исходной численной погрешностью(неточностью). Хаотическое поведение возникает по причине нелинейности уравнений Гамильтона с первоначально близкими траекториями,которые экспоненциально расходятся в ограниченной области фазового пространства. В связи с тем, что исходные условия могут быть измерены только с ограниченной точностью и ошибки распространяются с экспоненциальной скоростью, поведение таких систем в большом(протяженном) диапазоне не может быть предсказано. Воздействие возмущений на установление областей не интегрируемости может быть описано для слабых возмущений при помощи теоремы КАМ. Теорема КАМ, первоначально сформулированная Колмогоровым и строго доказанная Арнольдом и Мозером, применима для анализа возмущающих решений для классической многомерной (many-body) проблемы. В теореме КАМ утверждается, что при наличии малого возмущения оно ограничено N-тором, за исключением пренебрежимо малого наборах условий, который может приводить к блуждающему движению на потенциальном рельефе. Это блуждающее движение является хаотическим и приводит к большой (высокой) чувствительности к исходным условиям. В этом случае N-торы именуются поверхностями КАМ. При наблюдении в виде сечений плоскостью они часто именуются кривыми КАМ, такими как показанные на фиг. 2. Эти поверхности и кривые могут быть слегка деформированы (возмущены), при этом, для достаточно малого консервативного гамильтоновского возмущения, большинство нерезонансных инвариантных торов не будет принимать нулевое значение, а скорее будет претерпевать небольшую деформацию, так что в фазовом пространстве возмущенной системы будут иметься также инвариантные торы, заполненные фазо 5 выми кривыми, которые являются условно периодическими. На фиг. 2 показан набор инвариантных торов КАМ, на поверхности которых лежат эллиптические интегрируемые решения. Неинтегрируемые решения, непостоянные пути, которые являются гиперболическими по своей природе, лежат между инвариантными торами в так называемых резонансных зонах, которые также иногда именуют как стохастические зоны. Результаты КАМ были расширены за счет работы Мазера (J. Mather). Теория КАМ имеет отношение к движениям и соответствующим орбитам, которые слишком близки друг к другу,чтобы иметь хорошее поведение и быть стабильными. Так как теория КАМ в основном представляет собой анализ возмущения, то по самой природе постоянная (коэффициент) возмущений должна быть очень малой. Сильные отклонения от исходного оператора по параметру возмущения будут делать недействительным использование исходных собственных функций,которые были применены для генерирования набора возмущенных собственных функций. В работе Мазера проведен анализ нестабильных движений, которые далеки от того, чтобы их поведение можно было характеризовать как хорошее. Возмущение может быть относительно сильным, причем могут генерироваться совершенно новые собственные функции (решения). Практическая важность работы Мазера для вывода на планетарную орбиту, захвата и схода с нее состоит в том, что динамика применяется в тех областях фазового пространства (то есть в областях Мазера), которые объединены с трехи четырехмерными проблемами. Мазер показал,что для хаотических областей с размерами более низкого (второго) порядка для любой консервативной гамильтоновской системы существуют или остаются эллиптические орбиты, которые являются нестабильными. В терминах околоземных объектов (NEO (near-Earth object области КАМ и Мазера являются важными для описания как орбитального движения комет, так и баллистических (облет планеты, сближение космических аппаратов (КА), и перехват) траекторий к кометам и другим околоземным объектам с экономией топлива. Приведенное обсуждение является кратким изложением статьи автора John L.Remo, озаглавленной Орбиты околоземных объектов и нелинейная динамика: краткий обзор и интерпретации, "NEO OrbitsAcademy of Sciences 176-194 (1997), причем указанная публикация включен в данное описание в качестве ссылки, в том числе вместе с содержащимися в ней ссылками. Начиная с первых лунных экспедиций в 1960-е годы Луна остается представляющим интерес объектом как для научных исследова 002665 6 ний, так и для потенциального коммерческого развития. В течение 1980-х годов национальными космическими агентствами было организовано несколько лунных экспедиций. Интерес к исследованию Луны возрастает по мере создания международной космической станции, которая может быть использована как платформа,позволяющая производить запуски к Луне с низкой (низко стационарной) околоземной орбиты. Однако непрерывный интерес к исследованию Луны и возможность создания лунной базы зависят частично от возможности планирования (организации) частых и экономически выгодных лунных экспедиций. Типичная лунная экспедиция содержит следующие этапы. Первоначально запускают космический корабль с Земли или с низкой околоземной орбиты с достаточным импульсом на единицу массы или с возможностью изменения скорости, чтобы поместить космический корабль на орбиту Земля-Луна. Эта орбита является главным образом эллиптической орбитой вокруг (относительно) Земли, имеющей апогей,выбранный для практического совпадения с радиусом орбиты относительно лунной поверхности. При приближении космического корабля к Луне создают изменение скорости для перевода космического корабля с орбиты Земля-Луна на орбиту вокруг Луны. После этого может быть предусмотрено дополнительное изменение скорости для перевода космического корабля с орбиты вокруг Луны для посадки на ее поверхность, если такая посадка предусмотрена. При осуществлении обратного путешествия на Землю создают еще одно изменение скорости, достаточное для перевода космического корабля на орбиту Луна-Земля, которая, например, может быть аналогична орбите Земля-Луна. Наконец,при приближении космического корабля к Земле, требуется изменение скорости для перевода космического корабля с орбиты Луна-Земля на низкую околоземную орбиту или на траекторию возврата на Землю. На фиг. 3 показана орбитальная система для проведения обычной лунной экспедиции в не вращающейся системе координат, в которой ось Х 10 и ось Y 12 лежат в плоскости, определенной орбитой относительно поверхности Луны 36, а ось Z 18 расположена нормально к ней. При проведении обычной лунной экспедиции космический корабль запускают с поверхности Земли 16 или с низкой околоземной орбиты 20,которая не обязательно является круговой, и создают достаточную скорость для вывода космического корабля на орбиту Земля-Луна 22. Вблизи от Луны 14 предусматривают изменение скорости для уменьшения энергии космического корабля относительно луны и переводят космический корабль на орбиту вокруг Луны 24, которая не обязательно является круговой. Затем предусматривают дополнительное 7 изменение скорости для перевода космического корабля с орбиты вокруг Луны 24 для посадки на луну по траектории посадки 25. При необходимости возврата на Землю создают изменение скорости, достаточное для перевода космического корабля на орбиту Луна-Земля 26, либо непосредственно с лунной поверхности, либо за счет множества импульсов, как и при спуске. Наконец, вблизи от Земли 16 предусматривают изменение скорости для снижения энергии космического корабля относительно Земли и возврата космического корабля на низкую околоземную орбиту 20 или на Землю 16 по траектории возврата на Землю 27. На фиг. 4 показана другая обычная орбитальная система, описанная в патенте США 5, 158, 249 на имя Апхоффа (Uphoff), который включен в данное описание в качестве ссылки вместе с содержащимися в нем ссылками. Орбитальная система 28 включает в себя множество орбит вокруг Земли, причем переход между ними производится за счет использования гравитационного поля луны. Гравитационное поле Луны использовано для позиционирования за счет относительно малых среднеорбитных изменений скорости, для лунных условий пертурбационных траекторий (swingby), которые позволяют обеспечить желательную орбиту. Несмотря на то, что орбиты относительно Земли в орбитальной системе 28 могут быть выбраны таким образом, что все они имеют одну и ту же постоянную Якоби, что означает, что переходы между ними могут быть обеспечены без создаваемого ракетным топливом изменения скорости в номинальном случае, все же могут потребоваться относительно небольшие создаваемые ракетным топливом изменения скорости. Создаваемые ракетным топливом изменения скорости могут потребоваться для коррекции ошибок позиционирования при предшествующих лунных пертурбационных траекториях для осуществления выбора между достижимыми альтернативными орбитами при заданной пертурбационной траектории, а также для учета изменений постоянной Якоби, вызванных эксцентриситетом орбиты 36 относительно поверхности Луны. На фиг. 4 запуск космического корабля производится с Земли 16 или с низкой околоземной орбиты на орбиту Земля-Луна 22. Орбита Земля-Луна 22 может содержать, например,траекторию Земля-Луна с энергией, близкой к минимальной, например, орбиту, имеющую расстояние апогея, которое практически совпадает с радиусом орбиты 36 относительно поверхности луны. Космический корабль входит в лунную сферу гравитационного влияния 30 и использует гравитационное поле для перехода на первую орбиту 32 относительно Земли. Первая орбита 32 относительно Земли содержит, например, ориентировочно половину витка главным образом близкой к круговой ор 002665 8 биты одного лунного месяца, которая имеет полубольшую ось и эксцентриситет главным образом такие же, как и орбита относительно поверхности Луны 36, которая наклонена ориентировочно на 46,3 относительно плоскости,определенной орбитой 36 относительно поверхности Луны, и которая начинается и заканчивается в пределах сферы притяжения Луны 30. Так как первая орбита относительно Земли 32 и типичная орбита Земля-луна 22 с энергией, близкой к минимальной, имеют одну и ту же постоянную Якоби, то переход может быть осуществлен за счет использования поля притяжения Луны. На фиг. 5 показана еще одна орбитальная система, в которой, например, имеется орбита спутника вокруг Земли. Центральная станцияSC расположена у центра сферической зоны перекрытия треугольной формы Z. Два геосинхронных спутника S-А и S-B имеют эллиптические орбиты с идентичными параметрами. Этими параметрами могут быть, например, следующие:- апогей около 50,543.4 км,- перигей около 21,028.6 км,- ось мениска 42,164 км,- наклонение 63,- аргумент перигея 270,- эксцентриситет орбиты 0.35. Каждый спутник имеет антенну или антенны 11 и 12, причем каждая антенна ориентирована в направлении на центральную станцию в течение периода, когда спутник движется над зоной перекрытия. Центральная станция включает в себя станцию подключения и станцию управления. На фиг. 5 показан также подвижный блок М (который расположен в пределах зоны Z, но для большей ясности показан на фиг. 5 над этой зоной). Этот подвижный блок оборудован антенной 14, ось которого постоянно обращена главным образом в направлении зенита. Для управления указанными спутниками с такой станции возможно использование ряда стратегий. Пример одной из возможных стратегий показан на фиг. 6. В этой стратегии использована ракета ARIANE IV и требуются три импульса. В момент запуска спутник сопровождается обычным геостационарным спутником. Два спутника выходят на стандартную переходную орбиту ракеты ARIANE IV, причем эта орбита расположена в квазиэкваториальной плоскости(наклонение 7) с перигеем 200 км, апогеем 36,975 км и аргументом перигея 178. На фиг. 6 эта орбита отмечена как OST. Вблизи от перигея производят зажигание для получения первого импульса спутниковой ракеты, желательного для повышения апогея до 98,000 км, причем орбита остается в той же самой плоскости (орбита 01). Указанный импульс может быть подразделен на два или три импульса. Вблизи от апогея орбиты 01 новый импульс посылают на спутник для изменения плоскости 9 его орбиты. Наклонение этой плоскости близко к наклонению плоскости окончательной орбиты, а именно, составляет 63. Это тяговое усилие (толчок) является самым мощным и может быть разбито на два или три тяговых усилия. После этого спутник переходит на орбиту 02. Наконец, в соответствующей точке этой орбиты на спутник посылают третье тяговое усилие для обеспечения его окончательной орбиты. Несмотря на то, что описанная стратегия и является удовлетворительной в некоторых аспектах, она все же имеет недостаток. Действительно, требуется, чтобы плоскость орбиты была наклонена при переходе от орбиты 01 к орбите 02, что приводит к существенному потреблению топлива. На фиг. 7 показана схема другого известного принципа перехода с содействием силы притяжения Луны. В этом случае спутник прежде всего переводят на стандартную орбиту 01,расположенную в пределах квазиэкваториальной плоскости, которая на практике представляет собой орбиту OST фиг. 6, известную как геостационарная переходная орбита GTO (Geostationary Transfer Orbit). В точке Т 1 спутник переводят на окололунную орбиту 02, все еще расположенную в пределах квазиэкваториальной плоскости. На практике выбирают такую эллиптическую орбиту, большая ось которой ориентировочно равняется удвоенному расстоянию от Земли до луны, а именно, составляет около 768,800 км. Спутник входит в сферу притяжения луны SI и покидает эту сферу по траектории 03, плоскость которой сильно наклонена относительно экваториальной плоскости. В точке Т 2 спутник переводят на окончательную орбиту 04,которая находится в той же самой плоскости,что и орбита 03. Описанная выше орбитальная система подробно описана в патенте США 5,507,454 на имя Далка (Dulcк), который включен в данное описание в качестве ссылки вместе с содержащимися в нем ссылками. Далк стремится свести к минимуму необходимость использования двигателей реактивной системы управления за счет использования известной техники содействия лунной гравитации. Спутник прежде всего переводят в окрестность Луны за счет перелета (перехода) Хомана(Hohmann). Затем он летит под воздействием лунного притяжения в правильном направлении и с нужной скоростью, после чего производят два или три маневра. Этот способ является работоспособным, однако, размеры указанного маневра ограничивают применимость этого способа только для эллипсов с достаточно большим эксцентриситетом. Для обеспечения экономии при проведении указанного большого маневра необходимо иметь достаточно малый окончательный маневр. Автор настоящего изобретения пришел к выводу о том, что все приведенные выше орби 002665 10 тальные системы и/или способы обладают недостатком, связанным с необходимостью существенного расхода топлива для проведения маневров и поэтому являются недостаточно эффективными. Автор настоящего изобретения также пришел к выводу о том, что все приведенные выше способы сфокусированы на создании орбитальных систем, которые сконцентрированы на взаимосвязи между Землей и Луной и не используют и/или не принимают в расчет возможные эффекты применения за рамками этой проблемы двух тел. Таким образом, желательно создать орбитальную систему и/или способ, которые позволяют эффективно использовать горючее или ракетное топливо. Также желательно создать орбитальную систему и/или способ, которые являются главным образом независимыми от существенных тяговых усилий. Также желательно создать орбитальную систему и/или способ, которые учитывают эффекты лунного захвата (выхода на траекторию вокруг луны) и/ или земного захвата в большей степени, чем просто проблему двух тел. Также желательно создать орбитальную систему и/или способ, в которых используется компьютерная система, расположенная на борту космического корабля или спутника, или расположенная в центральной зоне управления. Также желательно создать орбитальную систему и/или способ, которые позволяют космическому кораблю иметь повторяющиеся близкие приближения как к Земле, так и к Луне. Также желательно создать орбитальную систему и/или способ, которые ограничиваются относительно малым расходом ракетного топлива,что обеспечивает эффективный способ для перемещения между Землей и Луной. Также желательно создать орбитальную систему и/или способ, которые не требуют больших изменений скорости, обеспечиваемых за счет ракетного топлива. Также желательно создать орбитальную систему и/или способ, которые позволяют размещать габаритные компоненты космического корабля. Также желательно создать орбитальную систему и/или способ, которые могут быть использованы для проведения как космических экспедиций с людьми, так и без них. Также желательно создать орбитальную систему и/или способ, которые позволяют космическому кораблю или спутнику иметь повторяющиеся близкие приближения при различных наклонениях как к Земле, так и к Луне. Также желательно создать орбитальную систему и/или способ, которые позволяют космическому кораблю или спутнику производить изменения наклонения относительно, например,Земли и/ или Луны. Отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбиталь 11 ную систему и/или способ, которые позволяют эффективно использовать горючее или ракетное топливо. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/или способ, которые являются главным образом независимыми от существенных тяговых усилий. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/или способ, которые учитывают эффекты захвата Луной и/или захвата Землей в большей степени, чем просто проблему двух тел. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/или способ, в которых используется компьютерная система, расположенная на борту космического корабля или спутника, или расположенная в центральной зоне управления. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/или способ, которые позволяют космическому кораблю иметь повторяющиеся близкие приближения как к Земле, так и к Луне. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/ или способ, которые ограничиваются относительно малым расходом ракетного топлива, что обеспечивает эффективный способ для перемещения между Землей и Луной. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/ или способ, которые не требуют больших изменений скорости, обеспечиваемых за счет ракетного топлива. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/ или способ, которые позволяют размещать крупногабаритные компоненты космического корабля. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/ или способ, которые могут быть использованы для проведения как космических экспедиций с людьми, так и без них. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/ или способ, которые позволяют космическому кораблю или спутнику иметь повторяющиеся близкие приближения 12 при различных наклонениях как к Земле, так и к Луне. Другой отличительной характеристикой и преимуществом настоящего изобретения является то, что оно дает возможность создать орбитальную систему и/или способ, которые позволяют космическому кораблю или спутнику производить изменения наклонения относительно,например, Земли и/или Луны. В соответствии с настоящим изобретением предлагается орбитальная система и/или способ,которые позволяют производить перемещения между Землей и Луной с существенно сниженным расходом ракетного топлива для проведения лунных экспедиций. В соответствии с настоящим изобретением также предлагаются орбитальные системы, полезные для перемещений от Земли к Луне и от Луне к Земле, в которых нет прямого использования гравитационного поля Луны для достижения межорбитального перехода и которые могут удовлетворяться относительно малыми расходами ракетного топлива. В соответствии с настоящим изобретением дополнительно обеспечены возможности для частого возвращения на Землю как оборудования, так и людей, находящихся на лунной поверхности или на окололунной орбите. В соответствии с настоящим изобретением также предлагаются орбитальные системы, полезные для перемещений по орбитам Земля-Луна, Земля-Земля, Луна-Земля/Земля и/или для проведения межпланетных экспедиций, причем в указанных системах использованы границы области слабой (малой) устойчивости для вывода на орбиту и/или для проведения изменений наклонения, что необходимо для проведения межорбитальных переходов и что может быть обеспечено за счет относительно малых расходов ракетного топлива. Настоящее изобретение основано, частично, на обнаружении автором того факта, что известные способы и/или орбитальные системы,которые сфокусированы или сконцентрированы на зависимости между Землей и Луной, не используют и/или принимают в расчет другие возможные эффекты за пределами этой проблемы двух тел. Более конкретно, автор настоящего изобретения предлагает новый способ и орбитальную систему, которые рассматривают вывод на орбиту (захват луной), экспедицию к Луне и выход на лунную траекторию, по меньшей мере, как проблему трех тел. Эта, по меньшей мере, проблема трех тел включает в себя (учитывает) взаимные связи между Землей, Луной и Солнцем, в том числе и взаимные связи относящихся к этому гравитационных сил. В соответствии с первым вариантом осуществления настоящего изобретения, предложен способ генерирования операционного перехода на баллистическую траекторию, для объекта главным образом с поверхности Земли или с околоземной орбиты, для достижения поверх 13 ности Луны или лунной орбиты с использованием процесса с внедрением компьютера. Указанный способ включает в себя операции ввода параметров, в том числе величины скорости VE,угла наклона траектории полета YE, и внедрение процесса переднего позиционирования за счет изменения величины скорости VE, а также угла наклона траектории полета YE, для обеспечения сходимости переменных позиционирования на Луне. Переменные позиционирования включают в себя радиальное расстояние rm и наклонение im. Указанный способ также включает в себя операцию итерации процесса переднего позиционирования до достижения достаточной сходимости для обеспечения операционного перехода на баллистическую траекторию с Земли или с околоземной орбиты до Луны или до окололунной орбиты. В соответствии с другим вариантом осуществления настоящего изобретения, предложен способ изменения, по меньшей мере, только наклонения или высоты объекта, который представляет собой, по меньшей мере, космический корабль, спутник или ракету. Указанный способ включает в себя последовательные и не последовательные операции перемещения с Земли или с околоземной орбиты до обеспечения слабого лунного захвата в области слабой устойчивости WSB или на орбите WSB, а также осуществление незначительного маневра и, опционно,осуществление изменений наклонения в WSB или на орбите WSB для схода с них. Указанный способ также включает в себя операцию перемещения с WSB или с орбиты WSB на Землю или на околоземную орбиту с заданной случайной высотой и, опционно, при наличии изменений наклонения. В соответствии с еще одним вариантом осуществления настоящего изобретения, предложен способ изменения, по меньшей мере,только наклонения или высоты объекта, который представляет собой, по меньшей мере, космический корабль, спутник или ракету. Указанный способ включает в себя последовательные и не последовательные операции перемещения с Земли или с околоземной орбиты до обеспечения слабого лунного захвата в WSB или на орбите WSB, а также осуществление маневров вокруг Луны за счет осуществления первого незначительного маневра в WSB или на орбитеWSB. Указанный способ также включает в себя операции опционного осуществления изменения наклонения в WSB или на орбите WSB и выхода из WSB или схода с орбиты WSB за счет осуществления второго незначительного маневра, а также предусматривает операцию перемещения из WSB или с орбиты WSB на Землю или на околоземную орбиту с заданной случайной высотой и, опционно, при наличии изменений наклонения. Указанные ранее и другие дополнительные характеристики изобретения будут более ясны 14 из последующего детального описания, данного в качестве примера, не имеющего ограничительного характера и приведенного со ссылкой на сопроводительные чертежи, которые являются неотъемлемой частью настоящего изобретения. Следует также иметь в виду, что использованная в данном описании терминология также не имеет ограничительного характера. Специалисты легко поймут, что концепция, на которой основано данное описание, легко может быть использована в качестве основы для проектирования иных конструкций (структур), способов и систем, выполняющих различные задачи настоящего изобретения. Поэтому важно иметь в виду, что формула изобретения перекрывает все такие эквивалентные конструкции, не выходящие за рамки настоящего изобретения и соответствующие его духу. Кроме того, задачей приведенной выше вводной части (аннотации) является предоставление возможности ознакомления соответствующего патентного ведомства и заинтересованных лиц, а в особенности ученых, инженеров, практиков в данной области с патентными или юридическими терминами или понятиями,чтобы иметь возможность при поверхностном ознакомлении быстро определить природу и сущность технического описания настоящего изобретения. Эта вводная часть ни в коей мере не предназначена для определения настоящего изобретения, что соответственно сделано в формуле изобретения, а также не предназначена для какого-либо ограничения объема патентных притязаний настоящего изобретения. Указанные ранее и другие характеристики изобретения, совместно с различными характеристиками его новизны, содержатся в приложенной формуле изобретения, образующей его неотъемлемую часть. Для лучшего понимания настоящего изобретения, его рабочих преимуществ и специфических задач, решаемых за счет его применения, далее будет сделана ссылка на сопроводительные чертежи и их описание, связанное с показанными на чертежах преимущественными вариантами осуществления настоящего изобретения. На фиг. 1 показана интегрируемая система с двумя степенями свободы на торе, а также замкнутая орбита траектории. На фиг. 2 показан набор инвариантных торов КАМ, на поверхности которых лежат эллиптические интегрируемые решения. На фиг. 3 показана орбитальная система для проведения обычной лунной экспедиции в не вращающейся системе координат. На фиг. 4 показана другая орбитальная система. На фиг. 5 показана другая орбитальная система, в которой, например, спутники вращаются вокруг Земли. На фиг. 6 показана другая орбитальная система, в которой, например, для вывода спут 15 ников на орбиту вокруг Земли использована ракета ARIANE IV и требуются три импульса. На фиг. 7 показана схема другого известного принципа перехода с содействием силы притяжения Луны. На фиг. 8 показан пример способа интегрирования вперед, таким образом, что конечное состояние интегрирования вперед совпадает с началом состояния, определенного интегрированием назад. На фиг. 9 показан пример операционного выхода на орбиту (ВСТ), определенного интегрированием вперед в соответствии с настоящим изобретением. На фиг. 10 показан другой пример операционного выхода на орбиту (ВСТ), определенного интегрированием вперед в соответствии с настоящим изобретением. На фиг. 11 приведена блок-схема концепции взаимодействия между цифровым интегратором и генератором исходных условий. На фиг. 11 А приведена детальная блоксхема взаимодействия между цифровым интегратором и генератором исходных условий. На фиг. 11 В приведена другая детальная блок-схема взаимодействия между цифровым интегратором и генератором исходных условий. На фиг. 12 приведена сводка различных лунных экспедиций. На фиг. 13 показан пример баллистического схода с орбиты BET (Ballistic Ejection Transfer) с возвратом на Землю с границы области слабой (малой) устойчивости WSB (Weak Stability Boundary), на любую желательную высоту и наклонение. На фиг. 14 показан стандартный маневр для изменения наклонения. На фиг. 15 показан маневр для изменения наклонения за счет схода космического корабля с околоземной орбиты и осуществления изменения наклонения на удалении от Земли. На фиг. 16 А-16 В показан маневр для изменения наклонения за счет баллистического вывода космического корабля/спутника на траекторию вокруг Луны при помощи ВСТ, маневрирования вокруг Луны на границе области слабой устойчивости WSB на промежуточной орбите, с последующим возвратом на Землю за счет баллистического схода с орбиты BET. На фиг. 17 показан главный центральный процессор (компьютер) для проведения компьютерной обработки информации в соответствии с одним из вариантов настоящего изобретения. На фиг. 18 приведена блок-схема аппаратных средств компьютера, показанного на фиг. 17. На фиг. 19 показан пример запоминающего устройства, которое может быть использовано совместно с накопителями на (магнитных) дисках, показанными на фиг. 17-18. На фиг. 20 показан другой вариант осуществления настоящего изобретения, в соответст 002665 16 вии с которым маневр для изменения наклонения за счет баллистического вывода космического корабля/спутника на траекторию вокруг Луны производится при помощи хомановского(Hohmann) вывода на орбиту, маневрирования вокруг Луны на границе области слабой устойчивости WSB на промежуточной орбите, с последующим возвратом на Землю за счет баллистического схода с орбиты BET. На фиг. 21 показан еще один вариант осуществления настоящего изобретения, в соответствии с которым маневр для изменения наклонения за счет баллистического вывода космического корабля/спутника на траекторию вокруг Луны производится при помощи хомановского(Hohmann) вывода на орбиту, маневрирования вокруг Луны на границе области слабой устойчивости WSB на промежуточной орбите, с последующим возвратом на Землю за счет другого хомановского схода с орбиты. Последующее детальное описание может быть представлено в терминах программных операций (алгоритмов), которые осуществляются на компьютере или в компьютерной сети. Эти описания алгоритмов предназначены для наиболее эффективного ознакомления специалистов с существом работы. Предложенная методика задумана в данном случае и везде, где в этом есть необходимость, как самосогласованная последовательность операций, приводящая к искомому результату. Указанные операции представляют собой физические манипуляции, которые следует произвести с физическими величинами. Обычно, хотя и не обязательно, указанные величины имеют вид электрических или магнитных сигналов, которые могут быть введены в запоминающее устройство, переданы (перенесены), сравнены или же обработаны иным необходимым образом. Время от времени удобно,главным образом по причинам повсеместного использования, именовать эти сигналы как биты, величины, элементы, символы, знаки, термины, числа и т. п. Однако следует иметь в виду, что все эти и другие аналогичные обозначения связаны с соответствующими физическими величинами и являются просто удобными этикетками для применения с ними. Кроме того, проводимые манипуляции часто обозначаются в таких терминах как добавление или сравнение, которые часто связывают с операциями в уме, производимыми человеком-оператором. Следует иметь в виду, что никакие такие способности человека-оператора не являются необходимыми или желательными в большинстве случаев при проведении описанных здесь операций, образующих часть настоящего изобретения, так как все такие операции являются машинными операциями. Полезными машинами для осуществления операций в соответствии с настоящим изобретением являются 17 цифровые компьютеры общего применения или иные аналогичные устройства. Настоящее изобретение имеет также отношение к созданию устройства для осуществления указанных операций. Такое устройство может быть специально сконструировано для решения поставленной задачи или же может включать в себя компьютер общего назначения с избирательной его активизацией или реконфигурацией при помощи введенной в него компьютерной программы. Представленные здесь операции (методики) не связаны с каким-либо конкретным типом компьютера или другого устройства. В некоторых случаях различные(вычислительные) машины общего применения могут быть использованы для выполнения программ, написанных в соответствии с указаниями, содержащимися в данном описании, а в других случаях более удобно провести конструирование более специализированной аппаратуры для осуществления предусмотренных операций. Из приведенного описания можно определить структуру, которая требуется для создания таких машин. При полете ракеты с Земли на Луну по классическому прямому пути, именуемому перелетом Хомана (Hohmann), который занимает всего только три дня, ее двигатели должны быть включены для торможения при выводе на лунную орбиту, так как в противном случае ракета будет перелетать Луну (проскакивать мимо нее) со скорость около 1 км/ с. Типичная лунная экспедиция предусматривает следующие этапы. Первоначально запускают космический корабль с Земли или с низкой околоземной орбиты с достаточным импульсом на единицу массы или с возможностью изменения скорости, чтобы вывести космический корабль на орбиту Земля-Луна. Эта орбита является главным образом эллиптической орбитой относительно Земли, имеющей апогей, выбранный для практического совпадения с радиусом орбиты относительно лунной поверхности. При приближении космического корабля к Луне обеспечивают изменение скорости для перевода космического корабля с орбиты ЗемляЛуна на орбиту вокруг Луны. После этого может быть предусмотрено дополнительное изменение скорости для перевода космического корабля с орбиты вокруг Луны для посадки на ее поверхность, если такая посадка предусмотрена. При осуществлении обратного путешествия на Землю создают еще одно изменение скорости,достаточное для перевода космического корабля на орбиту Луна-Земля, которая, например, может быть аналогична орбите Земля-Луна. Наконец, при приближении космического корабля к Земле, требуется измерение скорости для перевода космического корабля с орбиты ЛунаЗемля на низкую околоземную орбиту или на траекторию возврата на Землю. 18 Ракетное топливо, которое требуется для осуществления каждой из указанных выше операций, зависит от массы космического корабля и от изменений скорости, требующихся для осуществления межорбитального перехода,причем изменение скорости на каждом этапе обеспечивается главным образом за счет сжигания ракетного топлива. В этом случае продукты сгорания массы ракетного топлива истекают из космического корабля с высокой относительной скоростью, сообщая оставшейся массе космического корабля реактивное изменение скорости. С практической точки зрения, по той причине,что межорбитальные переходы во время известных лунных экспедиций производят за счет сжигания ракетного топлива, число и величина межорбитальных переходов, которые могут быть осуществлены при проведении лунной экспедиции, в большой степени зависят от массы космического корабля. Всегда существовало мнение о том, что нереально войти в область притяжения Луны без проведения замедления с использованием двигателей. В соответствии с настоящим изобретением, предлагается система и/или способ перемещения между Землей и Луной, который позволяет главным образом снизить расход ракетного топлива для осуществления Лунной экспедиции. В соответствии с настоящим изобретением предлагаются также орбитальные системы, полезные для перелета от Земли к Луне и от Луне к Земле, в которых нет прямого использования гравитационного поля Луны для обеспечения межорбитальных переходов и которые могут удовлетворяться относительно малыми расходами ракетного топлива. В соответствии с настоящим изобретением дополнительно обеспечены возможности для частого возвращения на Землю как оборудования, так и людей, находящихся на лунной поверхности или на окололунной орбите. В соответствии с настоящим изобретением также предлагаются орбитальные системы, полезные для перемещений по орбитам Земля-Луна, Земля-Земля, Луна-Земля/Земля и/или для проведения межпланетных экспедиций, причем в указанных системах использованы границы области слабой (малой) устойчивости для вывода на орбиту и/или для проведения изменений наклонения, что необходимо для проведения межорбитальных переходов и что может быть обеспечено за счет относительно малых расходов ракетного топлива. При подлете космического корабля к Луне за счет хомановского перелета, он имеет гиперболический избыток скорости около 1 км/с. Таким образом, для вывода на эллиптическую окололунную орбиту космический корабль должен быть заторможен с использованием ракетных двигателей, причем требующийся для этого расход ракетного топлива может быть существенным. Более того, существует относи 19 тельно короткий промежуток времени для проведения маневра торможения, чтобы перейти на окололунную орбиту. Способность космического корабля выйти на эллиптическую окололунную орбиту на лунной периапсиде без использования торможения ракеты именуется баллистическим выводом на орбиту (баллистическим захватом). Бельбруно (Belbruno) был первым, кто нашел путь для осуществления этого в 1986 г. для космического корабля с электрическими тяговыми двигателями, что опубликовано в работеAIAA/DGLR/JSASS Inter. Elec. Propl. Conf., May 1987, которая включена в данное описание в качестве ссылки вместе со всеми содержащими в ней ссылками. Бельбруно понял, что для осуществления баллистического захвата (баллистического вывода на орбиту) космический корабль должен приблизиться к Луне в состоянии слабого захвата, то есть космический корабль должен иметь скорость на желательном радиусе захвата,позволяющую балансировать между захватом и уходом (промахом). Предполагаемая область в окрестности Луны, где это происходит, именуется границей слабой устойчивости (Weak Stability Boundary (WSB или размытой границей,см. Belbruno, E., Lunar Capture Orbits, a MethodMatematica (CRM) Preprint n. 270, December 1994, причем все указанные публикации включены в данное описание в качестве ссылки вместе с содержащимися в них ссылками. При введении понятия области (границы) слабой устойчивости (WSB) проблема баллистического захвата сводится к проблеме достижения указанной области (то есть к приближению к Луне на желательной высоте при правильной скорости). Так как WSB находится между захватом и уходом, то космический корабль не должен иметь четко определенного цен 002665 20 трального космического тела (Земли или Луны),поэтому его движение должно быть достаточно точным (прецизионным). По этой причине представляется, что передний ньютоновский поиск (поиск вперед) позиционирования этой области из окрестностей Земли не будет успешным, что и на самом деле кажется правдой. Эта проблема была разрешена при помощи обратного метода, предложенного Байрнсом (D.Byrnes) в 1986 г. Этот метод был использован для нахождения точных баллистических выводов на траекторию (баллистических захватов) ВСТ при проведении современных космических экспедиций и при их подготовке, начиная сInt.Symp. on Small Satellite Systems and Services,Annecy, France, June 1996, причем все указанные публикации включены в данное описание в качестве ссылки вместе с содержащимися в них ссылками. Обратный метод стартует (начинает применяться) в желательном положении захвата у(игрек) относительно границы области слабой устойчивости WSB недалеко от Луны, где оскулирующий (соприкасающийся) эксцентриситет еM1. Используя указанное как исходное положение производят интегрирование в обратном времени. По причине особой чувствительности указанной области незначительное увеличение скорости в положении у может приводить космический корабль к уходу от Луны в обратном времени. Интегрирование прекращают в периапсиде в точке х относительно Земли. Обычно эта точка отличается от исходной точки х 0 для космического корабля. После этого определяют баллистический захват ВСТ за счет интегрирования вперед от x0 до х. Путь от точки х до точки захвата у уже был определен. Экономия V за счет баллистического захвата уменьшается на VM за счет несовпадения со скоростью в точке х, которая требуется для проведения маневра. Это абст 21 рактно показано на фиг. 8. В попытке уменьшения VM применяют вариации различных параметров. В случае LGAS, x0 находится на высоте 200 км от поверхности Земли, а х составляет 100,000 км. Точка у находится на расстоянии 30,000 км над северным лунным полюсом. Космическому кораблю потребуется около одного года для постепенного спуска по спирали с использованием его ионных двигателей с малой тягой до точки х, где VM равно нулю. Участок перехода от х до у в области слабой устойчивости WSB, где еM = 0, занимает 14 дней. Указанный метод вновь был использован Бельбруно (Belbruno) при содействии МиллераHiten. (См. приведенные ранее публикации,включенные в данное описание в качестве ссылки). При проведении экспедиции Hiten не имели достаточное количество ракетного топлива для захвата Луной за счет хомановского перелета, так что использование баллистического захвата ВСТ было единственным возможным вариантом. В этом случае для эллиптической орбиты Земли радиальное расстояние периаптики в точке х 0 составляло 8,900 км. Положение точки захвата у в области слабой устойчивостиWSB находилось на расстоянии 100 км над северным лунным полюсом, где соприкасающееся=0,94. Под влиянием возмущений солнца обратное интегрирование от у приводит космический корабль к периапсиде Земли в точке х на расстоянии 1,2 млн км от Земли. Очень малое V,составляющее всего только 14 м/с в точке х 0,было достаточно для перемещения космического корабля Hiten в х, где VM=30 м/с. Время полета составило 150 дней. Эта область слабой устойчивости WSB была использована в 1991 г.,когда космический корабль Hiten прибыл на Луну 2 октября этого года. Этот тип баллистического захвата ВСТ,использованный при полете космического корабля Hiten, может быть использован для любых лунных экспедиций, когда условия запуска на Земле и условия захвата на Луне являются произвольными. Для улучшения применимости этого типа баллистического захвата к экспедициям общего назначения необходимо произвести обобщение и сделать его более гибким. Совместная работа в течение 1992-1993 гг. позволила найти пути адаптации подхода с обратной интеграцией для экспедиций общего назначения, в том числе позволила найти благоприятные периоды времен для запуска. (Tandon, S.,Lunar Orbit Transfers using Weak Stability Boundary Theory, McDonnell Douglas Internal Report(Huntington Beach), March 1993). Однако этот метод является громоздким и по-видимому труден для автоматизации, так как он должен глав 002665 22 ным образом удовлетворять шести орбитальным элементам на Земле. Совместная работа была сфокусирована на баллистическом захвате ВСТ при отсутствии маневра по х. За счет тщательной настройки условий области слабой устойчивости лунного захвата WSB по у, не составляет труда настроить обратное интегрирование таким образом,чтобы траектория возвращалась на Землю с желательной высотой rE в точке x0. В действительности для этого достаточно иметь вариации еM в области слабой устойчивости WSB для третьего и более высокого десятичного разряда. Время полета составляет всего 80 дней, однако, при его проведении отсутствует управление наклонением, iE. Если стартовать в точке х 0 и затем попытаться перейти к желательному наклонению, то сразу будет ясно, что это невозможно. Даже изменение iE в тысячном разряде вызывает отклонение алгоритма позиционирования вперед при позиционировании назад к условиям WSB. Эта проблема может быть разрешена за счет более сложного обратного интегрирования с изменением множества лунных переменныхM, M, eM для достижения корректных значений как для iE, так и для iE, однако, при этом переменные M, M остаются удовлетворительными. Указанная методика является сложной и предусматривает сравнение множества контурных схем элементов Земли и проведение обратных интегрирований. В конечном счете они могут удовлетворяться, однако, этот подход занимает много времени. Автор настоящего изобретения нашел набор переменных относительно Земли, который позволяет провести весьма гибкое и имеющее хорошее поведение позиционирование вперед для баллистического захвата лунных условий с использованием изменения двух переменных на Земле, причем эти переменные не изменяют процесс. Такими переменными являются: 1. Значение скорости; 2. Угол наклона траектории полета. Автор настоящего изобретения также обнаружил путь эффективного нахождения баллистический захвата ВСТ при использовании относительно простого способа позиционирования вперед от х 0 до у, который является весьма надежным. Этот способ позиционирования вперед оказался способом 2 Х 2, при котором производят изменение двух переменных на Земле в ньютоновском алгоритме позиционирования,для достижения условий WSB на Луне с использованием двух лунных элементов. При осуществлении указанного способа большинство представляющих интерес переменных на Земле в процессе разъединяются, что позволяет контролировать rE, iE, E. Далее приведены несколько примеров указанного способа. Для того, чтобы осуществлять надежный поиск с Земли из заданной точки x0 до достиже 23 ния условий WSB на Луне в точке у, алгоритм должен сходиться к баллистическому захвату ВСТ с большими первоначальными ошибками при достижении желательных лунных условий. Независимые переменные, которые изменяют в точке x0 для достижения указанных лунных условий, должны быть развязаны от возможно большего числа угловых элементов Земли, в том числе от iE, E, E. Предполагается, что поиск проводят с периапсиды в момент времени ТE,ориентировочно равный нулю. Все три указанные угловые переменные могут быть достаточно ограниченными в зависимости от средства запуска. Например, для ракеты Arianne IV, iE = 7, E = 8 (West), E = 178. Представляющие интерес переменные цели на Луне, которые должны удовлетворяться,представляют собой радиальное расстояние, rM,и наклонение, iM. Для экспедиции Blue Moon можно принять rM = 2238 км, что отображает высоту 500 км, и iM = 90. Выяснилось, что если космический корабль падает в направлении к Луне с расстояния около 1-1,5 млн км, вблизи от апоапсиды Земли, которая является ориентировочно эллиптической, то он попадает в лунную область слабой устойчивости WSB, если геометрия Земля-Луна-Солнце является правильной. Координатная система у Земли, которая требуется для осуществления алгоритма позиционирования в точке х 0, имеет сферические координаты, которые заданы при помощи rE,долготы E, широты Е, величины скорости VE,угла наклона траектории полета YE, и азимута траектории полета E. Азимут траектории полета представляет собой угол от положительной оси z местной декартовой системы координат до вектора скорости YE, = (х, у, z). Более конкретно,E = cos-1 (z/VE) Была произведена фиксация rE = 6563.94 км, что соответствует высоте 186 км для BlueMoon. Алгоритм позиционирования получали путем вариации VE, YE для достижения rM, iM. Был использован стандартный алгоритм Ньютона второго порядка, что может быть выражено символически как:VE, YE,rM, iM. Была проведена проверка независимостиiE, E от VE, YE, причем нашли, что поиск 2 Х 2,описанный выражением (1), не изменяет iE, E. В результате, как только (1) сходится к баллистическому захвату ВСТ для заданных iE, E,они могут быть изменены и (1) можно прогнать(повторно выполнить) еще раз. Это делают, взяв конвергированные значения VE, YE, совместно с другими четырьмя фиксированными сферическими переменными, и трансформируя их в классические элементы. В классических элементах iE, E изменяют по желанию. 24 Затем классическое состояние трансформируют обратно в сферические координаты. Новое сферическое состояние все еще будет иметь старые конвергированные значения VE,YE (так как VE, YE являются независимыми от iE,E), однако, E, E, E будут изменены. Если это не слишком много, то (1) будет сходиться. Указанным образом можно систематически приводить iE, E к их желательньм значениям за счет повторного прогона (1) конечное число раз. Остающейся переменной, которая не имеет управления, является . Имеются несколько подходов, которые могут быть использованы для управления этой переменной, начиная от выбора даты запуска с Земли до использования контуров или импликации маневра. Как правило, хорошей идеей является конструирование контуров времени полета (Tf), iE, E, E за счет изменения M, M. Данные для таких контуров получают за счет систематического измененияM, M, и для каждой отдельной переменной,регулируя еM таким образом, чтобы траектория в обратном времени возвращалась на Землю при том же самом радиальном расстоянии, то есть при помощи 1 Х 1 ньютоновского позиционирования еMrE. Для каждого значения (M, M) проводят регистрацию значений (Tf, iE, E, E). Эти группы (массивы данных) могут быть использованы любое число раз в контурных программах. Контуры указанных переменных могут быть полезны для определения областей параметрического пространства, в том числе даты запуска с Земли,причем в этих областях могут быть найдены желательные значения для iE, E, E. Следует иметь в виду, что для запуска методики следует найти хорошее возможное значение (гипотезу) для VE, YE и для других сферических переменных, чтобы (1) сходилось. Для этого существует несколько путей, одним из которых является переход к классическим элементам и выбор аE, eE так, чтобы космический корабль был на эллипсе апоапсиды между 1 и 1,5 млн. км, и чтобы расстояние периапсиды было на желательной высоте. Например, реалистичными являются значения а = 657,666 км,е = .9900. Могут быть проверены и другие переменные, чтобы определить, происходит ли сходимость (1). Надежность (устойчивость к возможным воздействиям) выражения (1) показана в таблице 1, где отображено изменение iE нa два градуса от случая предыдущего схождения при iE = 21.56 (данные ЕМЕ) до 19.56. При проведении всего поиска сохраняли E = 36.51. Несмотря на то, что при первой итерации получили большое расстояние промаха, составившее 252,243 км, все же в результате добились сходимости. Результирующее время полета по итерации сходимости составило 93 дня, 5 ч, 13 мин. Проведенное обсуждение завершается документацией баллистического захвата ВСТ дляBlue Moon, которая разработана для средства выведения (ракеты) Arianne IV: 1. Вывод с Земли Т: 16 июля 1997 г. 06:16:55 (ЕТ)iM = 900 Этот баллистический захват ВСТ показан на фиг. 9. На фиг. 10 приведен другой пример операционного баллистического захвата ВСТ, полученного при помощи интегрирования вперед в соответствии с настоящим изобретением. На фиг. 10 показана баллистическая лунная траектория захвата. Участок Leg 1 этой траектории начинается на Земле, главным образом поблизости от Земли или на околоземной траектории, и идет до области слабой устойчивости ЗемляСолнце. Маневр 1 объединен с этим участком и может составлять, например, 11 м/с в области слабой устойчивости WSB Земля-Солнце. Альтернативно, сила тяги может быть рассчитана таким образом, что объект движется на траектории в области слабой устойчивости WSB ЗемляСолнце быстрее чем 11 м/с или даже приходит в область слабой устойчивости WSB при нулевой скорости. Объект проходит зону Луны по участку 1 ориентировочно тремя днями позже. Дополнительно, объект доходит до конца участка 1 ориентировочно через полтора месяца. В области слабой устойчивости WSB Земля-Солнце производят второй маневр на участке перемещенияleg 2, который переводит объект из области слабой устойчивости WSB Земля-Солнце на орбиту промежуток времени для перемещения по участку leg 2 занимает ориентировочно еще три месяца. В то время как подход с обратным интегрированием требует работы в течение целого месяца для нахождения операционной области слабой устойчивости WSB, предложенная новая методика с позиционированием вперед требует всего нескольких минут работы компьютера. Легко можно автоматизировать переход i, ,к их желательным значениям, однако, это легко сделать и вручную. Следует иметь в виду, что предложенная методика позиционирования является только вариантом 2 Х 2, что означает,что имеются только две переменные управления и две искомые переменные. Принимая во внимание природу баллистического вывода на траекторию (баллистического захвата), эта методика является элегантной. Для осуществления указанной методики требуются следующие программные средства: 1. Цифровой интегратор с возможностью позиционирования; 2. Генератор исходных условий. На фиг. 11 приведена блок-схема взаимодействия между цифровым интегратором 102 и генератором исходных условий IGUESS 100 в соответствии с настоящим изобретением. Интегратор является чрезвычайно точным и представляет собой стандартный интегратор 10-го порядка или же другой стандартный интегратор. Для позиционирования применен стандартный ньютоновский метод второго порядка. Указанный интегратор производит моделирование солнечной системы с научно достижимой точностью и использует планетарную эфемериду. Такая точность необходима потому, что предложенная методика позволяет получать операционные переходы (перелеты), которые желательны для осуществления реальных экспедиций и полетов. Нашли, что генерируемые интегратором траектории имеют пренебрежимо малую ошибку по сравнению с реальной траекторией космического корабля. Интегратор-устройство позиционирования имеет автономную исходная программу, написанную на языке FORTRAN. Указанное программное обеспечение интегратораустройства позиционирования включено в пред 27 варительную заявку на патент США 60/ 036,864, которая включена в данное описание в качестве ссылки. Генератор исходных условий дает хорошую исходную гипотезу (возможное значение) для желательных переменных позиционирования в сферических координатах и позволяет производить изменение с приращением (инкрементом) i, , , что необходимо для обеспечения сходимости позиционирования. Для интегратора - устройства позиционирования требуется точная планетарная эфемерида движения планет, которая представляет собой файл стандартных данных для планет. Этот файл, который именуется DE403 и может быть получен на JPL, включен в данное описание в качестве ссылки. Он используется в астрономии и в космонавтике во всем мире. Несмотря на то, что приведенное выше описание или процесс были сфокусированы на лунном захвате объекта, запущенного с Земли или с околоземной орбиты, указанный процесс может быть применен для межпланетных экспедиций и, опционно или преимущественно, в том случае, когда имеется гравитационный эффект солнца. Например, вместо перелета с Земли на Луну, что описано выше, можно выбрать другую пару космических объектов, например, перелет с Юпитера в область слабой устойчивости его спутника Европа. При этом может быть также осуществлен баллистический захват спутника Европа. Следует иметь в виду, что физическая реализация перелета с Юпитера на его спутник Европа главным образом аналогична перелету Земля-Луна. Для приложения приведенного выше процесса для этого случая необходимо просто заменить слово Земля на Юпитер и слово Луна на Европа. См., например, публикацию AAS 97-174, "Trajectory Design for aEuropa Orbital Mission," Sweetser et al., (Feb. 1012,1997), которая включена в данное описание в качестве ссылки. На фиг. 11 А приведена детальная блоксхема взаимодействия между цифровым интегратором и генератором исходных условий. Как это показано на фиг. 11 А, в методике в соответствии с настоящим изобретением применяют два различных типа переменных при поиске позиционирования, с использованием ньютоновского метода второго порядка (NM) 104 для устройства позиционирования и интегратора 10 го порядка (I) 106 для цифрового транслирования (копирования) орбиты (или траектории) с Земли на Луну. Для устройства позиционирования использован поиск 2 х 2 (хотя может быть использован поиск и другого размера), то есть изменяют на Земле две переменные (из шести) и находят (отслеживают) две переменные (из шести) на Луне. Наличие двух параметров (iM, rM) на Луне является достаточным. Для устройства позиционирования преимущественно используют 28 специальный набор из 6 переменных, именуемых сферическими координатами, две из которых изменяют таким образом, чтобы они достигали iM, rM (само собой разумеется, что настоящее изобретение предусматривает использование различных переменных, которые могут быть выведены (получены) с использованием настоящего изобретения). Указанными шестью переменными являются rE, E, sE, VE, YE, E. Двумя переменными, которые в действительности изменяют, являются VE, YE. При хорошем выборе (при правильной гипотезе) для VE, E получают сходимость позиционирования. Устройство IGESS 100 обеспечивает хороший первоначальный выбор для VE, YE. При работе устройства позиционирования используют интегратор I, причем этот интегратор используется много раз. Его задачей является определение путем итерации точных значений для VE, YE = VE, YE, таким образом, чтобы баллистический захват ВСТ доходил до Луны при желательных значениях iM, rM. От IGESS требуется всего одна гипотеза в начале процесса позиционирования. На фиг. 11 В приведена другая детальная блок-схема взаимодействия между цифровым интегратором и генератором исходных условий. Только что полученная баллистическая траектория ВСТ идет с Земли с заданным орбитальным состоянием до Луны, где rM, iM достигают их желательных значений. В описанном на фиг. 11 В процессе изменяют только VE, YE, а остальные четыре переменные rE, E, sE, E остаются фиксированными, поэтому в результате получаем шесть переменных rE, E, sE, VE, YE, E. Для получения операционного баллистического захвата ВСТ, на Земле необходимы 6 параметров орбиты, что именуется орбитальным состоянием. Их получают ранее времени начала экспедиции, причем все они должны обычно удовлетворять другому набору переменных, связанных с указанными выше, но отличающихся от них. Эти переменные представляют собой E, eE, iE, E, WE, TE, которые именуют классическими переменными. Указанное выше конвергированное (со схождением) состояние S = rE, E, sE, VE, YE, E позволяет получить конкретный набор классических переменных С = E, eE, iE, E, WE, ТE. Вообще значения классических переменных это не совсем то, что требуется для проведения экспедиции, так как для нее необходимо конкретное значение iE = iE, E, WE, и обычно приходится прибегать к особому приему (хитрости) для его нахождения. Другие параметрыVE, YE изменяются при использовании ньютоновского метода NM, то возникает осложнение. Однако iE, E являются независимыми от VE,YE, поэтому они остаются фиксированными при 29 сходимости NM. Таким образом, после конвертирования (обеспечения сходимости) NM, iE, E могут быть скорректированы для получения слегка отличающихся значений, при этом NM опять должен сходиться. При применении для этого итерации, iE, E могут постепенно приходить к искомым значениям, при использовании процесса по блок-схеме фиг. 11 А несколько раз. Наилучшим путем изменения iE, E является управление с учетом контурного пространства С, которое может быть найдено при помощи стандартных контурных программ (например,при помощи коммерческой программы CONT). Последней остающейся переменной являетсяWE, которая изменяется при работе NM, однако,это изменение незначительное и эта переменная также может быть приведена к ее желательному значению. Суммируя, можно сказать, что описанный на фиг. 11 В процесс применяют многократно при повторной итерации до тех пор, пока iE, E не получат желательные значения, причем для содействия этому применяют стандартные контурные программы. Затем WE приводят к желательному значению за счет повторного применения необходимое число раз описанного на фиг. 11 В процесса. В соответствии с другим вариантом настоящего изобретения также предлагаются орбитальные системы, полезные для перемещений по орбитам Земля-Луна, Земля-Земля, ЛунаЗемля/ Земля и/ или для проведения межпланетных экспедиций, причем в указанных системах используют границы области слабой устойчивости для вывода на орбиту и/ или для проведения изменений наклонения. Автор настоящего изобретения пришел к выводу о том, что стартовое положение от Земли для баллистического вывода на траекторию ВСТ, рассчитанного при помощи указанной методики, может быть на любой высоте, подходящей для любого средства запуска, в том числе и для строящейся международной космической станции Альфа, с использованием, например, революционного одноступенчатого вывода на орбиту транспортного средства, известного как Venture Star, с применением ракетных двигателей нового типа,которые разрабатываются фирмой Локхид. Автор настоящего изобретения также пришел к выводу о том, что ВСТ имеет ключевую характеристику, которая позволяет обеспечить существенную экономию Delta-V (изменения скорости) при изменении наклонений для спутников на орбите Земли, что описано далее более подробно. Когда спутник подходит к Луне в точке y баллистического захвата, то пренебрежимо малое Delta-V может заставить его покинуть Луну при инверсном баллистическом захвате, именуемым баллистическим сходом с орбиты BET 30 спутник назад к Земле из области слабой устойчивости WSB на любую желательную высоту и наклонение (см. фиг. 13). Это свойство следует из того числового факта, что пренебрежимо малое изменение эксцентриситета е относительно Луны для космического корабля в области слабой устойчивостиWSB будет вызывать сход с орбиты Луны. Автор настоящего изобретения пришел к выводу о том, что BET симметричен ВСТ, причем захват Луной на ВСТ происходит при нулевом Delta-V и сход с орбиты Луны на BET происходит при нулевом Delta-V. Указанному может способствовать незначительное увеличение эксцентриситета орбиты при нахождении в области WSB для перехода на BET с желательными свойствами, когда подход к Земле достигается на переапсиде Е 2. Более точно, нахождение в области WSB означает, что е 1 в момент времени t = t0. Удаление от Луны в более поздний момент времениt = t1t0 означает, что e(t1)1. Незначительное изменение е в момент времени t0 означает, что произошло изменение е до нового эксцентриситета е (t0)е (t0) + , гдеявляется пренебрежимо малым. (В примере, приведенном ранее на фиг. 9, баллистический захват в области WSB на высоте 100 км над северным лунным полюсом подразумевает, что е = .94. Увеличение е в четвертом десятичном разряде приводит к более позднему сходу с орбиты Луны в момент времени t = t1, который отличается от t0 только на несколько часов. Изменение е в четвертом десятичном разряде эквивалентно тому, что незначительное Delta-V вызывает сход с орбиты. В этом случае= .000 а. где а 0 представляет собой целое число 1,2, ,9). Для получения BET с желательными значениями hE, iE, спутник должен выйти из области WSB в правильном направлении и в нужный момент времени. Автор настоящего изобретения пришел к выводу о том, что наличие симметрии в проблеме трех тел доказывает существованиеBET с возвратом на Землю, ориентировочно симметричной ВСТ по положению и пространству скорости. Использованная для доказательства модель близка к идеализированной ограниченной проблеме трех тел между Землей, солнцем и спутником, когда такая симметрия должна существовать. При нахождении спутника за пределами области WSB после схода с орбиты или после захвата, эффект притяжения Луны является пренебрежимо малым. В фиксированной относительно солнца системе координат с центром на Земле, в которой ось х является линией Земля-Луна, BET может быть ориентировочно получена из ВСТ путем отражения относительно этой оси. Метод с интегрированием вперед позволяет их точно находить. Это свойство и его применения обсуждаются далее в следующем разделе. 31 Указанное свойство имеет важные последствия, так как оно позволяет решить проблему снижения по мере возможности объема (диапазона) Delta-V, необходимого для изменения наклонения спутников на орбите Земли. Этот факт может быть объяснен следующим образом. Начнем со спутника на случайной эллиптической орбите, Е 1, относительно Земли с наклонением iE,1. Если желательно изменение наклонения на другое значение iE,2, то тогда следует провести стандартный маневр, для чего требуется Delta-V. Этот маневр проводят на периапсиде. Чем больше изменение наклонения,то есть iE =iE,2 - iE,1, тем больше Delta-V (то есть VI). Например, если эллиптическая орбита относительно Земли является круговой на высоте hE, с соответствующей круговой скоростьюVc, то тогда получаем формулуVI=2VcSin(iE/2). Этот маневр производят нормально к плоскости орбиты (см. фиг. 14). Задачей является снижение величины VI. Это можно сделать, например, путем перевода спутника с его исходной эллиптической орбиты Е 1 с наклонением iE,1 за счет проведения маневра V1 у периапсиды эллипса. После этого спутник начнет удаляться от Земли. В некоторый более поздний момент времени, при достаточном удалении спутника от Земли в подходящем местоположении, производят маневр V2 для возвращения спутника к Земле, к периапсиде эллипса Е 2, который аналогичен Е 1, за исключением наклонения, которое изменилось наiE,2. У периапсиды проводят окончательный маневр V3, чтобы спутник перешел на окончательную орбиту Е 2 (фиг. 15). Производят сравнение VI с суммой=V1 + V2 + V3, которую желательно иметь меньше VI (VI). Это может быть в том случае, когда величина iE относительно велика, аV2 относительно мала. Экономия Delta-V составляет VI -. Одним из путей минимизации V2 является использование Луны (лунного притяжения). Попытка сделать это предпринята в патенте США No. 5,507,454 на имя Далка (J. Dulck), который включен в данное описание в качестве ссылки и в котором использована стандартная техника содействия лунной гравитации. Спутник прежде всего переводят в окрестность Луны за счет перелета Хомана (Ноhmаnn). Затем он летит под воздействием лунного притяжения в правильном направлении и с нужной скоростью,при этом производят два или три маневра для изменения V2. После этого спутник может быть возвращен на орбиту Земли за счет обратного перелета Хомана, когда наклонение изменяют от исходного значения iE,1 на iE,2. Этот способ является работоспособным,однако, V2 составляет ориентировочно 600 м/с. Размеры указанного маневра ограничивают 32 применимость этого способа только для эллипсов с достаточно большим эксцентриситетом,потому что для обеспечения экономии при наличии указанного большого маневра необходимо иметь достаточно малый окончательный маневр V1, V3. Возможность осуществления этого представляется при возможно больших эксцентриситетах Е 1, Е 2, то есть при наиболее близком приближении к 1. Размер такого маневра будет максимальным, когда эксцентриситеты равны 0 для круговых околоземных орбит. Это происходит потому, что больший эксцентриситет означает, что скорость на периапсиде эллипса является более высокой. Поэтому требуется меньшее значение скорости, чтобы спутник сошел с эллипса и подошел к Луне по хомановскому переходу или же был вновь захвачен Землей при другом обратном хомановском переходе. Метод Далка ограничен случаем или применим для орбит типа геоперехода, которые имеют большой эксцентриситет. Метод Далка относительно мало что дает в смысле экономии для низких круговых орбит. Автор настоящего изобретения пришел к выводу о том, что новый способ, который позволяет обеспечить гораздо лучшую экономиюVI, может быть получен за счет использования баллистического лунного захвата в областиWSB. Это происходит потому, что обсуждавшееся ранее свойство в данном случае подразумевает V2 = 0. Следует иметь в виду, что баллистический лунный захват совершенно отличен от стандартного содействия гравитации. При содействии гравитации гравитационное взаимодействие спутника с Луной моделируется в простой системе двух тел и не включает в себя Землю. Баллистический захват Луной в системе двух тел невозможен, так как в формулировке двух тел между Луной и, например, спутником, космическим кораблем или другим объектом, областьWSB не существует. Баллистический захват существует в модели трех тел между спутником или космическим кораблем, Луной и Землей,так как в этой формулировке область WSB существует. Собственно ВСТ существует в более сложной формулировке четырех тел между спутником, Луной, Землей и Солнцем и не существует, если в модель не включено солнце. Необходимость иметь V2 = 0 является весьма важной, причем при использовании ВСТ и BET можно получить существенно лучшую экономию по сравнению с ранее существовавшими методами. Кроме того, данный новый способ также является существенным для низких круговых околоземных орбит, которые широко применяются в системах связи и для которых не могут быть применены другие известные методы, как это было показано выше. 33 Более конкретно, в соответствии с данным новым способом прежде всего производят маневр V1 для перевода спутника на траекторию баллистического вывода ВСТ к Луне из Е 1, например, у периапсиды. Указанный способ и точный алгоритм для его осуществления описаны в предварительной заявке на патент СШАNo. 60/036,864, поданной 4 февраля 1997 г., которая включена в данное описание в качестве ссылки, причем указанный алгоритм вкратце обсуждается далее, хотя возможно применение и других аналогичных алгоритмов с получением аналогичных результатов. Выяснилось, что значение V1 является ориентировочно таким же,которое требуется для хомановского перехода,так что в данном случае нет существенной потери при выводе на ВСТ. Баллистический захват ВСТ позволяет привести спутник к слабому лунному захвату в области слабой устойчивости WSB на желательной высоте hL по истечении 80-100 дней полета. Это определяет эксцентриситет еL и полубольшую ось аL. Наклонение iL и другие лунные элементы, такие как аргумент периапсидыL и узел L, выбирают таким образом, чтобы спутник мог быть возвращен на Землю с желательным наклонением iE,2 относительно Земли и высотой периапсиды hE, которая требуется для Е 2. Спутник возвращается к Земле по траектории баллистического схода с орбиты BET за счет незначительного изменения лунных элементов. Точный алгоритм описан ниже, хотя возможно применение и других аналогичных алгоритмов с получением аналогичных результатов. Спутник приходит к земной периапсиде через 80-100 дней после выхода из областиWSB. Спутник должен находится в областиWSB возможно более короткое время, так как она является хаотической областью. Однако небольшой стабилизирующий маневр малой амплитуды может быть приложен непосредственно после баллистического захвата, так что спутник может находиться на орбите Луны месяц или более того, если требуется синхронизация. Затем после обеспечения синхронизации производят небольшой маневр для перевода спутника на траекторию BET к Земле. Это подразумевает V20. Когда спутник возвращается к периапсиде Земли, прикладывают V3 для перевода спутника на желательную эллиптическую орбиту Е 2. Этот маневр ориентировочно такой же, как и для обратного хомановского перехода, так что нет существенной потери при переводе спутника на траекторию BET к Земле у периапсиды Е 2. Символически можно записать: Е 1V1 ВСТзахват ЛунойV20 ВЕТV2 Е 2 (см. фиг. 16 А-16 В). К изложенному можно сделать два следующих замечания. Первое состоит в том, что 34 время полета может составлять 160-200 дней. Это следует учитывать при изучении полной экономии Delta-V. Другое замечание связано с общностью предложенного способа. Везде предполагалось, что форма и размер Е 1 остаются неизменными, то есть не меняются eE, aE, hE,что бывает не всегда, так как в ходе измененияiE,1 могут быть предусмотрены изменения и этих трех элементов. Преимущественно в более общем случае можно предположить, что Е 2 может иметь значения hE, eE, аE, которые отличаются от соответствующих значений для Е 1. Переменная hE представляет собой высоту над Землей либо исходной эллиптической орбиты Е 1, либо окончательной эллиптической орбиты Е 2, причем может быть установлено любое значение этой переменной hE. Поэтому в дополнение к получению произвольного изменения наклонения эта методика дает произвольное изменение высоты. Основной компьютерный процесс или алгоритм способа с интегрированием вперед описаны в предварительной заявке на патент СШАNo. 60/036,864, поданной 4 февраля 1997 г., которая включена в данное описание в качестве ссылки, хотя, как это уже упоминалось ранее,могут быть использованы также и другие функционально аналогичные алгоритмы. Далее приведено краткое изложение этого способа. На высоте периапсиды hE, производят изменение переменных Е 1, VE, YE для попадания в лунную область WSB с желательными iL, hL. Этот способ представляет собой квадратичный ньютоновский способ позиционирования, в котором совместно с точным цифровым интегрированием использована стандартная планетарная эфемерида DE403. Обычно требуется достаточно хорошая гипотеза для VE, YE, чтобы иметь сходимость позиционирования. Указанное описано в предварительной заявке на патент США 60/036,864, поданной 4 февраля 1997 г. Символически,VE, YEiL, hL Свойством указанного алгоритма является то, что E, iE остаются фиксированными, так что они могут быть систематически приведены к их желательным значениям для Е 1 за счет повторного применения алгоритма позиционирования. Переменная E может быть привязана за счет использования контурных графиков параметров Земли, описанных в предварительной заявке на патент США 60/ 036,864, а также за счет ее приведения к желательному значению за счет повторного применения алгоритма позиционирования. В данном алгоритме время подхода к Луне при баллистическом захвате, которое сокращенно называется A/D, также является свободным параметром. Момент времени, когда ВСТ покидает периапсиду Е 1, именуется датой выведения на орбиту I/D. 35 Указанным образом точный баллистический захват ВСТ может быть выработан при помощи компьютера, который удовлетворяет всем требующимся орбитальным элементам для Е 1 желательной даты выведения на орбиту I/D. Эту операцию проводят для ВСТ, показанного на фиг. 9. Конвергированное значение VE дает следующее V1 при вычитании значения скорости Е 1 у периапсиды:V1 = VE - GmE (1 + еE1)/rE где eE = eE1 представляет собой эксцентриситет Е 1, mE является массой Земли, а G представляет собой коэффициент гравитации. V1 увеличивает скорость Е 1 у периапсиды, так что спутник может войти в область баллистического захвата ВСТ. При подходе спутника к Луне в моментA/D у лунной периапсиде при баллистическом захвате в области WSB, производят определение элементов iL, hL, еL, поэтому значение Delta-V равно нулю. Остальными элементами являютсяL, L, L, где L представляет собой эксцентрическую аномалию. Так как в соответствии с настоящим изобретением предусматривается,например, использование оскулирующей лунной периапсиды, то L=0, и поэтому этот элемент также является заданным элементом. Таким образом, L, wL являются свободными. Предполагается, что эти элементы находятся в правильном местоположении в параметрическом пространстве, чтобы позволить произвести следующее позиционирование на Землю с использованием BET. Если же это не так, то тогда, как это определил автор настоящего изобретения, небольшой маневр стабилизации, ориентировочно 10 м/с, достаточен для того, чтобы спутник не выходил из области WSB Луны в течение ориентировочно одного месяца (см, например, ссылку 6, имеющуюся в предварительной заявке на патент США 60/036,864, поданной 4 февраля 1997 г., которая включена в данное описание в качестве ссылки, по определению вместе со всеми имеющимися в ней ссылками). Это дает достаточно времени для перемещения спутника в желательную для указанных элементов область параметрического пространства. Автор настоящего изобретения определил, что спутник может вращаться вокруг Луны в области WSB с незначительной Delta-V, так как его движение динамически сбалансировано и поэтому является достаточно чувствительным, так что небольшой маневр достаточен для обеспечения этого вращения. Эти маневры в совокупности должны составлять около 1 м/с. Указанный способ может быть также использован для обеспечения хранения оборудования в области WSB Луны в течение любого заданного промежутка времени. При проведении нацеливания (позиционирования) с Луны на периапсиду Земли с заданными значениями hE, iE,2 для Е 2 снова использу 002665 36 ется, например, способ с интегрированием вперед, однако, при старте с Луны вместо Земли. Используют изменение VL, YL на высоте hL для задания hE, iE,2, где VL представляет собой значение скорости относительно Луны. Символически,VL, YLhE, iE,2 Сходимость этого алгоритма приводит к баллистическому сходу с орбиты BET. Поэтому для BET могут быть использован такой же алгоритм позиционирования и такая же программа,что и для ВСТ. Программа позволяет также получить желательную траекторию, при времени полета спутника 80-100 дней. Время A/D прихода к периапсиде Земли для Е 2 определяют после схождения алгоритма позиционирования, так как A/D представляет собой свободный параметр при поиске позиционирования. Дата I/D схода с лунной орбиты BET, совместно с iL, L, которые являются фиксированными в соответствии с алгоритмом способа с интегрированием вперед, могут быть изменены вручную для получения заданных значения L,L для Е 2 у периапсиды Земли. Значение DeltaV, требующееся в соответствии с алгоритмом позиционирования, составляет, например, ориентировочно менее 1 м/с. Таким образом, полное изменение (Delta-V), использованное после захвата спутника луной, составляет ориентировочно 11 м/с. Таким образом, для V2 в результате получаем V20. Автор настоящего изобретения нашел, что у периапсиды Земли требуется маневр V3, который снижает скорость VE BET до скорости Е 2,что может быть определено по формуле:V3 = VE - G mE(1 + еE2)/rE в которой еE = еE2 представляет собой эксцентриситет Е 2. Преимущественно, в более широком аспекте можно предполагать, что Е 2 имеет значения hE, eE, аE, отличающиеся от соответствующих значений для Е 1. Переменная hE представляет собой высоту над Землей либо исходной эллиптической орбиты Е 1, либо окончательной эллиптической орбиты Е 2, причем может быть установлено любое значение этой переменнойhE. Поэтому, в дополнение к получению произвольного изменения наклонения, эта методика обеспечивает также произвольное изменение высоты. Краткое изложение методикиI. ВСТ с Е 1 до баллистического лунного захвата. При I/D = I/D у периапсиды Е 1 со значениями hE, iE,1 применяют способ с интегрированием вперед, определенный выражениями (1),для нахождения ВСТ. Затем приводят E, E к их желательным значениям с использованием повторного применения выражений (1). Конвергированное значение VE позволяет получитьV1 за счет использования выражения (2). Дату 37 подхода к Луне A/D1 определяют по способу с интегрированием вперед как свободную переменную.II. Подход к Луне и определение BET. В определенную дату A/D1, ВСТ выходит на периапсиду Луны с параметрами hL, iL, которые соответствуют операции I, причем V2 = 0. Производят стабилизацию за счет добавления,например, ориентировочно 10 м/с. При скорости, например, около 1 м/с перемещают спутник для достижения желательных значений L, L,так чтобы баллистическая траектория BET могла быть успешно нацелена на Землю. По истечении времени Т от даты A/D1, применяют способ с интегрированием вперед, определенный выражением (3). Вручную регулируют L, L и вновь применяют способ с интегрированием вперед, для нахождения E, E, которые необходимы для Е 2. Наконец, находят BET при условии I/D2 = A/D1 + Т. BET достигает периапсиды Земли в момент A/D2.BET достигает периапсиды Е 2 при hE, iE,2 в момент A/D2, как это было определено в соответствии с операцией II. Элементы iE,2, E, E подходят для Е 2. Остальные элементы аE, еE для Е 2 могут быть удовлетворительными после применения V2 в соответствии с выражением(4). Несмотря на то, что в соответствии с операциями I-III предусмотрена определенная вычислительная методика, могут быть использованы и другие методы вычислений (если они есть), которые функционально эквивалентны для выполнения основных функций, а именно:I. Нахождение ВСТ с орбиты Е 1 до баллистического лунного захвата;III. Нахождение BET с Луны на Е 2. Более того, указанный способ может быть использован для любой области в космическом пространстве, которая имеет свойства WSB,подходящие для определенной формы баллистического захвата. Кроме того, природа как ВСТ, так и BET облегчает эффективность и выполнимость вычислений. Сравнения экономии Delta-V Далее проведено краткое сравнение полной экономии Delta-V приведенного здесь способа, который можно назвать способом изменения наклонения WSB, WSB Inclination ChangeMethod, или сокращенно, WSB-ICM, со стандартным путем осуществления маневра для единичного изменения наклонения у периапсиды Е 1, который можно назвать классическим способом Classical Method или сокращенно просто СМ. Способ WSB-ICM также сравнивают со способом, описанным в ссылке (8), который можно назвать Hohmann Inclination Change 38 Сравнение проведено для случая изменения наклонения орбиты спутника, находящегося на круговой орбите Земли на высоте 700 км. Изменение наклонения для этого примера в случае перехода от iE,1 = 34 до iE,2 = 90 предусматривает iE = 56. Наклонение 34 ориентировочно соответствует наклонению для Vandenberg AFB в Калифорнии. Этот тип изменения наклонения может быть применим для спутников сети Teledesic. Кроме того, сеть Iridium также планирует запускать спутники на низкие круговые полярные орбиты. Рассчитали, что как для способа WSB-ICM, так и для способа HICM V1 = V3 = 3.080 км/с. Из ссылки (8), V2670 м/с для H-ICM. Для WSB-ICM V20. Для СМ при изменении наклонения Delta-V равно 7.050 км/с. Если предположить, что V1 представляет собой полное изменение Delta-V,использованное для изменения наклонения, то тогда для WSB-ICM, H-ICM, CM мы имеет соответствующие значения V1 = 6.160, 6.830,7.050 км/с. Это дает соответственно процентную экономию относительно способа СМ, составляющую 13,3,0%. Таким образом, экономия способаWSB-ICM существенно превышает экономию двух других способов, ориентировочно на 13%. Указанные данные сведены в табл. 1 и 2 в конце описания заявки. Способ WSB-ICM дает в основном улучшение относительно способа СМ при iE49% в случае круговых орбит на высоте 700 км, хотя возможна экономия и для другихiE. Типично критическое значение зависит от высоты периапсиды и эксцентриситета E1, E2. Другим интересным случаем является изменение наклонения круговой орбиты на указанной высоте 700 км от 7 до 90. Это может быть применено для случая средства запуска(ракеты) Arianne IV или Arianne V. В случае СМ имеется значение 9.945 км/с. Способ WSB-ICM позволяет снизить это значение на 38%, до такого же значения, что и в предшествующем параграфе, а именно, до 6.160 км/с. Это означает,что ракета Arianne IV или Arianne V может быть использована с таким же улучшением на 13%,при использовании способа WSB-ICM для изменения наклонения до 90 от 7, в сравнении со способом СМ. Следует подчеркнуть, что степень улучшений Delta-V зависит от высот периапсиды,эксцентриситетов и наклонений E1, E2. Было отмечено, что при сравнении с примером, приведенным в ссылке (8) для околоземных орбит типа геоперехода, способ WSB-ICM дает улучшение относительно H-ICM ориентировочно на 33%. Эта экономия Delta-V при ее пересчете в экономию массы космического корабля с использованием уравнения ракеты, позволяет, за счет уменьшения массы ракетного топлива, выводить на орбиту большее число спутников при 39 помощи данного средства вывода. Кроме того,при меньшей полезной нагрузке можно использовать средство запуска меньшего класса. Обе указанные возможности могут иметь коммерческое значение для спутниковой сети, используемой в системах связи. На фиг. 17 показан основной центральный процессорный блок (компьютер) 218, который может быть использован для внедрения способа обработки информации в соответствии с одним из вариантов описанных здесь ранее способов в соответствии с настоящим изобретением. Показанная на фиг. 17 компьютерная система 218 включает в себя центральный процессорный блок 234, который имеет накопители 236 и 238. Обозначение 236 и 238 для накопителей является чисто символическим и обозначает, что определенное их число может быть использовано в данной компьютерной системе. Обычно используют накопитель на гибком магнитном диске 236 и накопитель на жестком диске, который на фиг. 17 не показан ни внутри, ни снаружи, а также накопитель на компакт-диске CD ROM,обозначенный в виде слота 238. Число и тип накопителей может быть различным для различных конфигураций компьютера. Компьютер имеет также монитор 240 для вывода на него(визуальной) информации. Обычно в системе имеется также клавиатура 242 и мышь 244, которые представляют собой средство ввода со стандартным интерфейсом. На фиг. 18 приведена блок-схема внутренних аппаратных средств компьютера, показанного на фиг. 17. Как это показано на фиг. 18,шина данных 248 использована в качестве основного тракта информации для обеспечения связи между элементами компьютерной системы. Центральный процессорный блок (ЦП) 250 представляет собой устройство, в котором производятся вычисления и осуществляются логические операции, требующиеся для выполнения программы. Постоянное запоминающее устройство (ПЗУ) 252 и запоминающее устройство с произвольной выборкой (ЗУПВ) 254 образуют основную память компьютера и могут быть использованы для хранения данных моделирования. Дисковый контроллер 256 взаимодействует с одним или несколькими накопителями на магнитных дисках с использованием системной шины 248. Таким накопителями могут быть накопители на гибких магнитных дисках, такие как 262, внутренние и внешние накопители на жестких дисках, такие как накопители 260, а также компакт-диск CD ROM или цифровой видео диск DVD (digital video disks), такой как 258. Интерфейс 264 подключен к монитору 240 и позволяет выводить информацию с шины 248 на монитор 240. Сообщение с внешними устройствами может быть обеспечено при помощи портов связи 266. 40 На фиг. 19 показан пример запоминающего устройства, которое может быть использовано в качестве накопителя, такого как 262 на фиг. 18 или 236 на фиг. 17. Обычно запоминающее устройство, такое как накопитель на магнитном диске, CD ROM или цифровой видео диск DVD содержит, среди прочего, программную информацию для управления компьютером, так чтобы компьютер мог выполнять функции проверки и развития в соответствии с предусмотренным для описанной здесь компьютерной системы. Несмотря на то, что показана система обработки, которая включает в себя единственный процессор, единственный накопитель на жестком диске и единственное локальное запоминающее устройство, система обработки также может быть снабжена множеством процессоров или устройств хранения информации, или их комбинацией. Указанная система обработки в действительности может быть заменена любой подходящей системой обработки (или скомбинирована с ней), которая работает в соответствии с принципами настоящего изобретения и включает в себя сложные (продвинутые) вычислительные устройства, настольные универсальные компьютеры, миникомпьютеры, суперкомпьютеры и переносные компьютеры типа ноутбук, а также вычислительные сети с комбинацией указанных компьютеров. Архитектура обычных вычислительных систем обсуждается более подробно в книгеStallings, MacMillam Publishing Co.(3rd ed. 1993); вопросы проектирования обычной сети вычислительных систем обсуждаются более подробно в книге Data Network Design, Darren L. Spohn,McGraw-Hill, Inc. (1993), а общие вопросы передачи данных обсуждаются более подробно в книге Data Communications Principles. R.D. Gitlin, J.F. Hayes and S.B. Weinstain, Plenum PressProfessional Publishing (2nd ed. 1992). Каждая из указанных публикаций включена в данное описание в качестве ссылки. В соответствии с альтернативным вариантом осуществления настоящего изобретения,упомянутый выше процессор, в особенности микропроцессорная схема, могут быть заменены любой подходящей схемой обработки информации (или скомбинированы с ней), которая включает в себя программируемые логические устройства, такие как PALs (programmable arrayPLAs (programmable logic array, программируемые логические матрицы), цифровые процессоры для обработки сигналов DSPs (digital signalprocessors), программируемые пользователем матрицы логических элементов FPGAs (fieldprogrammable gate arrays), интегральные схемы специального применения ASICs (applicationcircuits) и т.п. Можно указать, что стартовое положение с Земли для ВСТ, рассчитанной в соответствии с описанной здесь методикой, может находиться на любой высоте, желательной для средства запуска, например, для такого как строящаяся международная космическая станция Альфа, с использованием, например, революционного одноступенчатого вывода на орбиту транспортного средства, известного как Venture Star, с применением ракетных двигателей нового типа,которые разрабатываются фирмой Локхид. Использование области FB позволяет производить другие переходы с малой энергией к астероидам и Марсу, а также из этих местоположений, с использованием так называемого резонансного биения. Подводя итог, можно сказать, что предложенная методика позиционирования вперед для получения операционных баллистических захватов ВСТ существенно проще для применения и быстрее, чем обратный подход. Она представляет собой методику 2 Х 2, позволяет производить расчет захватов ВСТ в ходе прямого процесса и является надежной. Захваты ВСТ могут быть рассчитаны для любых стартовых положений относительно Земли или для условий подхода к Луне. Как было указано здесь ранее, один из путей существенного снижения полного Delta-V(изменения скорости) для изменения наклонения спутника, вращающегося на эллиптической орбите вокруг Земли, указан в предварительной заявке на патент США 60/041,465, поданной 25 марта 1997 г., а также в соответствующей заявке РСТPCT/US 98/05784, которые включены в данное описание в качестве ссылки. Этот путь представляет собой так называемый способWSB, где WSB является сокращением (акронимом) от выражения Weak Stability Boundary,область слабой устойчивости. Проведено сравнение указанного снижения с классическим путем изменения наклонения, что осуществляется при помощи единственного маневра V1, измеренного в км/с, у периапсиды исходной эллиптической орбиты Е 1 с наклонением iE1, причем указанный маневр производят нормально к плоскости орбиты. Это вызывает переход с Е 1 на другую эллиптическую орбиту Е 2, которая имеет такой же эксцентриситет и высоту периапсиды, что и орбита Е 1, однако, с новым наклонением iE2. Это показано на фиг. 3 в предварительной заявке на патент США 60/041,465,а также на фиг. 14 настоящего изобретения. Для сравнения можно указать, что в соответствии со способом WSB применяют, например, три маневра Vi, где i = 1,2, 3. Первый маневр производят на периапсиде Е 1 на высоте 42 вить спутник к Луне с осуществлением баллистического вывода на траекторию (баллистического захвата) ВСТ (Ballistic Capture Transfer). Спутник приходит ориентировочно через 85 дней в область WSB на желательной высоте hL относительно Луны и с наклонением iL. Позже спутник уходит от Луны при помощи небольшого маневра V20 и возвращается на Землю за счет BET ориентировочно еще через 85 дней(BET означает Ballistic Ejection Transfer, баллистический сход с орбиты). Окончательный маневр V3 производят на желательной высоте hE2 периапсиды, чтобы вновь вывести спутник на эллиптическую орбиту Е 2 вокруг Земли с желательным наклонением iE2 и эксцентриситетом еE2, причем, в более общем случае, hE1, еE1 не обязательно равны hE2, eE2. Полное время полета составляет ориентировочно 170 дней. Эта методика показана, например, на фиг. 5 в предварительной заявке на патент США 60/ 041,465, а также на фиг.15-16b описания настоящего изобретения. Для простоты на указанных чертежах эксцентриситеты и высоты периапсид E1, E2 сохранены неизменными. Как это было показано здесь ранее, при определенных условиях, = V1 + V2 + V3VI. Это позволяет обеспечить существенную экономию полного изменения Delta-V в различных ситуациях, например, в случае важного применения при изменении наклонения от 34, вVandenberg AFB, до 90 для круговых орбит на фиксированной высоте 700 км, что может быть применено в области систем связи, причем экономия в данном случае составляет 13% по сравнению с классическим методом. Экономия 13% является существенной и может быть использована для достижения существенной экономии ракетного топлива или,что эквивалентно, массы. Это, в свою очередь,может привести к уменьшению массы спутника,а более легкий и меньший по размерам спутник может быть создан при помощи новых способов проектирования. Это позволяет также производить одновременно запуск на орбиту большего числа спутников. С другой стороны, даже без применения новых способов проектирования спутников,более легкий спутник позволяет использовать более легкое (менее мощное) средство запуска на орбиту. В табл. 2 в предварительной заявке на патент США 60/041,465 показано, что достигнута экономия на 36% полного Delta-V для изменения наклонения от 7 до 90 в сравнении со стандартным методом. Это обеспечивает конкурентоспособность средства запускаArianne по сравнению с выводом на орбиту с космодрома в Вандерберге (Vandenberg). Областью улучшения для способа WSB является то, что время полета составляет ориентировочно 170 дней. Способ WSB основан на 43 догадке автора настоящего изобретения, связанной с тем, что лунная область WSB представляет собой чувствительную область на границе лунного захвата и ухода. Приходящий в эту область спутник имеет нестабильный захват. Это означает, что хотя его орбитальное состояние и является эллиптическим, орбитальное состояние в области WSB, как определил автор настоящего изобретения, является близким к параболическому. Это означает, что орбитальное состояние близко к сходу с орбиты или к захвату, причем,как определил автор настоящего изобретения,стандартная кеплеровская энергия двух тел относительно Луны является отрицательной или близкой к нулю. Приходящий в эту область спутник делает это хаотически, поэтому достаточно малого изменения Delta-V для выхода спутника из этой области. С другой стороны,автор настоящего изобретения также определил,что малое изменение Delta-V может стабилизировать захват спутника. Существование области WSB объясняется гравитационными взаимодействиями между Землей и Луной. Она представляет собой пограничную область на грани балансирования гравитационных взаимодействий для движущегося спутника. (Более подробно это описано в предварительной заявке на патент США 60/036,864, поданной 4 февраля 1997 г., а также в заявке РСТPCT/US 98/01924 и в имеющихся в них ссылках, причем все они включены в данное описание в качестве ссылки). По той причине, что область WSB является чувствительной при входе в нее, эта чувствительность может быть использована для баллистического схода с орбиты BET спутника с малым Delta-V и с любым желательным наклонением относительно Земли. Это обеспечено по замыслу автора тем, что баллистический сход с орбиты BET проводят достаточно далеко от Земли, например, ориентировочно на расстоянии 1 млн км (так как меньшие расстояния дают меньший эффект), так чтобы гравитационные возмущения солнца могли воздействовать на спутник достаточно долго для того, чтобы при его возврате на Землю он мог иметь желательное наклонение (iE2). Сход с орбиты с малымDelta-V или при его использовании гарантирует,что V20 или является весьма малым. Автор настоящего изобретения определил,что лунная область WSB в физическом трехмерном пространстве может быть реализована на заданной высоте и при заданном положении относительно Луны путем задания критического или определенного значения скорости. Это, в свою очередь, приводит к получению критического или определенного значения эксцентриситета захвата. Для обеспечения сходимости положим hL = 100 км, хотя возможна и другая высота. Это подразумевает, что еL = .94 для данного примера. 44 Таким образом, автор настоящего изобретения также определил, что способ WSB позволяет уменьшить полное изменение Delta-V по той причине, что для достижения этого используют ВСТ. Это означает, что изменение Delta-V захвата ориентировочно равно нулю или же очень мало. Другое преимущество WSB состоит в том, что после прихода к Луне незначительное изменение Delta-V стабилизирует захват, причем спутник может вращаться вокруг Луны в области WSB при небольшом Delta-V для осуществления синхронизации и позиционирования ранее его схода с орбиты. Эти возможности обеспечивают экономию 13% по сравнению с описанным здесь ранее классическим методом. Автор настоящего изобретения также обнаружил, что изменение, которое может быть сделано для улучшения описанной техники для перелета от Земли у периапсиды Е 1 в областьWSB Луны, заключается не в использовании движения по ВСТ с временем полета 85 дней, а в использовании стандартного хомановского перелета с временем полета ориентировочно 3 дня. (Это значение 3 дня указано здесь как номинальное значение. Время полета для стандартного перехода до Луны может изменяться от 3 до 8 дней и больше. Кроме того, хомановский перелет может потребовать проведения маневра посредине маршрута, что здесь не предусмотрено). Было проверено, что на лунной периапсиде на высоте 100 км в области WSB спутник имеет гиперболический избыток скорости около 1 км/с. Для обеспечения захвата в области WSB следует приложить изменение Delta-V, чтобы вновь привести эксцентриситет к значению .94. Автор настоящего изобретения определил, что для этого требуется изменение около .200 км/с,которое можно обозначить как изменение (захват) Delta-V, а именно, VC, при этом, в случае ВСТ, VC = 0, и для хомановского перелета VCBET до Е 2 проводят как и раньше, где V20. Значение V1 остается ориентировочно таким же, как и при использовании ВСТ. Так как значение V3 остается таким же, то автор настоящего изобретения определил, что к бюджетуDelta-V WSB следует добавить .200 км/с, что является ценой использования хомановского перелета к Луне. Добавка .200 км/с к полному изменению Delta-V для способа WSB дает 6.360 км/с, которые требуются для изменения наклонения спутника на круговой орбите Земли с высотой 700 км от 34 до 90. Таким образом, вместо снижения Delta-V на 13% по сравнению с классическим методом,снижение становится равным 10%, что все еще является значительной экономией. Однако при этом получают существенное уменьшение времени полета от 170 дней до 88 дней. Этот модифицированный способ WSB можно назвать пер 45 вым модифицированным способом (First Modified WSB Method) или сокращенно M1-WSB(см. фиг. 20). Его параметры указаны в табл. 1 данного описания. Автор настоящего изобретения также обнаружил, что указанная в предыдущем параграфе модификация может быть дополнительно углублена. В соответствии со способом M1WSB спутник все еще возвращается к Земле к периапсиде Е 2 с использованием BET. Выход из области WSB с использованием BET происходит при незначительном Delta-V. Для более быстрого возвращения к Земле требуется большее изменение Delta-V, чтобы осуществить сход с орбиты с большей скоростью. Для возвращения к Земле по стандартному хомановскому переходу с высоты над Луной 100 км, когда оскулирующий эксцентриситет составляет .94, требуется Delta-V, которое составляет .200 км/с, чтобы обеспечить симметричный перелет аналогично подходу к Земле при способе M1-WSB,так что теперь V2 = .200 км/с. При добавлении этого значения к полному изменению Delta-V способа WSB в табл. 1 получаем Delta-V 6.560 км/с. Это составляет улучшение 7% по сравнению с классическим методом, что все еще является существенным. Однако полное время полета при этом уменьшается с 88 дней для способаM1-WSB всего только до 6 дней. Этот способ можно назвать вторым модифицированным способом (Second Modified WSB Method) или сокращенно M2-WSB. (См. фиг. 21 и таб. 1). Сравнение указанных способов WSB, M1WSB, M2-WSB с классическим способом С проведено в табл. 1. Символически они могут быть выражены следующим образом:M2 WSB: E1HWSBHE2,где Н обозначает хомановский переход. Способ M1-WSB, вероятно, представляет собой наиболее гибкий способ по причине использования BET при возврате. Так как BET представляет собой чувствительную траекторию, на которую воздействуют гравитационные возмущения Солнца, то легко может быть реализована возможность достижения любого желательного наклонения к Земле для орбиты Е 2. Возможность достижения желательного наклонения к Земле при возврате с использованием хомановского перехода может иметь ограничения по времени, так как на хомановский переход не воздействуют гравитационные возмущения солнца. При использовании способа M2-WSB, хомановский перелет (переход) с Луны к Земле происходит главным образом при движении в рамках расстояния Земля-Луна или в пределах гравитационного влияния, и не является достаточно далеким, чтобы можно было использовать Солнце для изменения его наклонения при под 002665 46 ходе к Земле. Поэтому, если только синхронизация не является идеальной, может потребоваться проведение существенного маневра посредине маршрута для достижения желательного земного наклонения. Таким образом, в некоторых ситуациях способ M2-WSB может быть достаточно ограниченным. Однако BET позволяет улучшить синхронизацию и опыт показывает, что такие переходы является более гибкими, чем хомановские переходы, причем маневры посредине маршрута за счет нежелательной синхронизации являются обычно достаточно малыми. Здесь мы полагаем, что они равны нулю, что часто имеет место. Программа и алгоритм, которые требуются для расчета ВСТ, и/или BET являются такими же, как описанные в предыдущей заявке, включенной в данное описание в качестве ссылки. Это автономная программа на исходном языке,которая является полностью описанной. Описанная в предыдущей заявке программа также позволяет провести расчет стандартного хомановского перехода с использованием аналогичного алгоритма Солнца, то легко может быть реализована возможность достижения любого желательного наклонения к Земле для орбиты Е 2. Возможность достижения желательного наклонения к Земле при возврате с использованием хомановского перехода может иметь ограничения по времени, так как на хомановский переход не воздействуют гравитационные возмущения солнца. При использовании способа M2-WSB, хомановский перелет (переход) с Луны к Земле происходит главным образом при движении в рамках расстояния Земля-Луна или в пределах гравитационного влияния, и не является достаточно далеким, чтобы можно было использовать Солнце для изменения его наклонения при подходе к Земле. Поэтому, если только синхронизация не является идеальной, может потребоваться проведение существенного маневра посредине маршрута для достижения желательного земного наклонения. Таким образом, в некоторых ситуациях способ M2-WSB может быть достаточно ограниченным. Однако BET позволяет улучшить синхронизацию и опыт показывает, что такие переходы является более гибкими, чем хомановские переходы, причем маневры посредине маршрута за счет нежелательной синхронизации являются обычно достаточно малыми. Здесь мы полагаем, что они равны нулю, что часто имеет место. Программа и алгоритм, которые требуются для расчета ВСТ, и/или BET являются такими же, как описанные в предыдущей заявке, включенной в данное описание в качестве ссылки. Это автономная программа на исходном языке,которая является полностью описанной. Описанная в предыдущей заявке программа также позволяет провести расчет стандартного хома 47 новского перехода с использованием аналогичного алгоритма. Все указанные выше способы, WSB, M1WSB, M2-WSB, которые для краткости названы просто способами WSB, предусматривают использование области WSB. Как это было описано здесь ранее, нелинейная природа областиWSB, а также то, что эта область находится между захватом и уходом, позволяют иметь захват и уход главным образом при нулевом или при относительно малом Delta-V. Указанное, совместно с гравитационными возмущениями солнца,позволяет существовать BET и ВСТ. ОбластьWSB существует благодаря взаимным гравитационным взаимодействиям Земли и Луны. Таким образом, при моделировании движения спутника в этой области должно быть проведено гравитационное моделирование как Земли,так и Луны, потому что при движении спутника область WSB можно рассматривать как границу взаимодействия указанных двух гравитационных полей. При расчете энергии спутника относительно Луны (так называемой кеплеровской энергии двух тел), когда он движется в области WSB,оказывается, что эта энергия является слегка отрицательной или близкой к нулю. Автор настоящего изобретения пришел к выводу о том,что тот факт, что энергия является слегка отрицательной означает, что имеется слабый захват спутника. Тот факт, что энергия близка к нулю означает, что спутник близок к уходу. Другая характеристика области WSB, которая не находит отражения в указанной кеплеровской энергии двух тел, состоит в том, что малый маневр может в действительности стабилизировать движение спутника, потому что хотя энергия и близка к нулю, малое снижение отрицательной энергии будет предотвращать легкий уход (сход с орбиты) спутника. Таким образом, областьWSB является тонкой по ширине в положительном пространстве скорости. Это означает,что небольшие изменения скорости будут стабилизировать движение спутника и, следовательно, выводить его из области WSB. Тот факт, что, как это было показано автором настоящего изобретения, область WSB существует только в динамической модели трех тел Земля-Луна-Спутник, совместно с его близкой к нулю кеплеровской лунной энергией, означает, что движение спутника в области WSB совершенно отличается от движения спутника при содействии гравитации с использованием Луны. В том случае, когда полет спутника вокруг Луны происходит с содействием гравитации, для этого достаточна модель только между Луной и спутником. Только это необходимо для расчета маневра с содействием гравитации. При этом спутник не находится вблизи области WSB для стандартного содействия гравитации в пространстве положение - скорость, которое требует ввода в модель и Земли. 48 Другое отличие между обсуждаемыми здесь способами WSB и стандартным содействием гравитации заключается в том факте, что когда полет спутника вокруг Луны происходит с содействием гравитации, то он имеет главным образом положительную кеплеровскую энергию относительно Луны, что означает, что движение должно быть гиперболическим. Это в корне отличается от движения в области WSB, которое является отрицательным и близким к нулю, при этом движение в области WSB является эллиптическим и параболическим. Моделирование движения в области WSB не может быть проведено без учета гравитационного влияния Земли,иначе область WSB не будет существовать. Таким образом, моделирование движения в области WSB не может быть проведено в рамках взаимодействия двух тел между спутником и Луной, поэтому оно отличается от движения спутника с содействием лунной гравитации. Приведенное объяснение показывает, что способы WSB отличаются от способов с содействием лунной гравитации. Это относится даже и к случаю M2-WSB, в котором используются переходы Хомана, так как спутник входит в область WSB, что подразумевает отличие этого способа M2-WSB от стандартного способа, в котором используется только содействие гравитации Луны. Наконец, следует подчеркнуть, что баллистический вывод на траекторию (баллистический захват) ВСТ представляет собой путь к Луне с наименьшей энергией, а хомановский переход обладает наибольшей энергией. Энергия ВСТ является наименьшей потому, что захват является баллистическим, что означает отсутствие необходимости в маневре. Кроме ВСТ, или BET, как это было показано здесь ранее, может существовать семейство переходов,которые лежат между хомановским переходом и ВСТ или BET. Указанные переходы имеют время полета, большее чем при хомановском переходе, и меньшее, чем при ВСТ или BET. Для них также необходимы значения VC, которые лежат между нулем и значением, применяемым для хомановского перехода. Аналогично, в случае BET значение V2 лежит между нулем и значением, применяемым для хомановского перехода. Из проведенного детального обсуждения выясняется множество характеристик и преимуществ настоящего изобретения, причем подразумевается, что приложенная формулы изобретения перекрывает все такие характеристики и преимущества настоящего изобретения,которые лежат в его рамках и соответствуют его духу. Например, в то время как ранее здесь обсуждался процесс с внедрением компьютера со ссылкой на выведение спутника на орбиту вокруг Земли с заданным наклонением, описанная Использование ВСТ может уменьшить эти выше техника (технология) может быть примерасходы наполовину или использовать их на нена или может иметь отношение к любому другие полезные цели при проведении лунных объекту, для которого необходимы изменения экспедиций. наклонения и/ или требуется проводить маневПроизошли три весьма важных события,ры для вывода на орбиту вокруг Земли или друкоторые могут привести к регулярным и частым гой планеты или тела в космическом пространполетам на Луну, начиная с 1999 г., и к постве, и/ или осуществлять в космическом простроению сначала небольшой лунной базы в странстве моделирование орбиты или создание течение ориентировочно 10 лет, а затем и к орбиты. Таким образом, описанные здесь техосуществлению больших коммерческих проекника/способ могут быть использованы вне завитов. симости от типа объекта и/или вида изменения 1. В июле 1996 г. фирма Локхид заключила наклонения. Описанная здесь техника (технолоконтракт на 1 млрд. долларов на разработку в гия) может быть использована как новый путь с масштабе 1/3 одноступенчатой орбитальной применением компьютера для обеспечения перакеты с использованием двигателя aerospike. ремещения между двумя точками в космичеЭта ракета называется Х-33. Это приведет к реском пространстве. Кроме того, описанная здесь волюционным изменениям для космических техника может быть применена в обратной сиполетов, которые станут такими же простыми,туации относительно вывода объекта на орбиту как и полет на реактивном самолете. Модель в вокруг Луны, когда объект уходит от Луны или меньшем масштабе выполнена в 1998 г., а полсходит с лунной орбиты. Например, объект мономасштабная версия должна быть готова в жет быть запущен с поверхности Луны, введен в 2002 г. Она именуется Venture Star, и NASA область WSB для проведения маневра и/или имеет планы по замене космических челноков изменения наклонения, а после этого возвращен на эту ракету. Нет сомнений, что появятся и на желательную орбиту вокруг Луны. версии меньшего размера, которые позволят Более того, в связи с тем, специалистами открыть космос для путешествий. легко могут быть осуществлены многочислен 2. В ноябре 1996 г. на Луне вблизи от ее ные модификации и изменения, нежелательно южного полюса была обнаружена вода в больограничивать настоящее изобретение точными ших и легко доступных количествах. Это ознаконструкциями и операциями, описанными и чает большую вероятность развития исследовапоказанными на чертежах, причем следует ний Луны, так как вода обеспечивает автономиметь в виду, что все такие подходящие модиность при работе на Луне. фикации и эквиваленты не выходят за рамки 3. Международная космическая станция настоящего изобретения. Альфа должна быть закончена в 2001 г. Это Планирование космических экспедиций на обеспечит постоянное существенное присутстпоследнюю декаду (двадцатого столетия) покавие в космосе, причем эта станция может быть зывает, что ВСТ начинает широко использоиспользована как пусковая платформа. ваться. Япония использовала ВСТ в 1998 г. в Уже планируются на 2000, 2001 гг. две экспедиции Lunar-A, а военно-воздушная акалунные экспедиции для исследования водных демия (Air Force Academy) США планирует исресурсов Луны и проводится обсуждение вопользовать ВСТ в 1998-1999 гг. в экспедиции проса о создании небольшой лунной базы. НетBlue Moon. В действительности компоненты сомнений в том, что после развертывания прополета Blue Moon уже проверены при запуске екта Venture Star последует коммерческое осракеты Атлас (Atlas) с мыса Канаверал 21 воение Луны с созданием сети отелей и т.п.,октября 1997 г. Из пяти проведенных в 1991 причем фирма Мицубиси и другие большие 1999 гг. экспедиций, в трех использовали ВСТ. японские корпорации уже обсуждают вопрос о Будущее использования Луны выглядит создании больших (лунных) гостиничных коммногообещающим. В течение последующих 10 плексов. лет на экспедиции к Луне планируется затратить миллиарды долларов. Изменения наклонения от 34 до 90 при помощи Delta-V. E1 Е 2. E1, Е 2 представляют собой круговые орбиты на высоте 700 км. Все изменения Delta-V указаны в км/с. Область WSB определена для захвата периапсиды на высоте 100 км, причем е = .94 Таблица 1 Экономия отн. С Время полета Способ ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ изменения, по меньшей мере,наклонения и высоты космического летательного аппарата в зоне притяжения, по меньшей мере, двух небесных тел, включающий следующие независимые стадии: а) осуществление перехода летательного аппарата с его орбиты относительно первого небесного тела или с поверхности первого небесного тела до обеспечения слабого захвата в области слабой устойчивости (WSB) или на орбите в области (WSB), связанной с первым и вторым небесными телами,б) проведение опционно в области WSB или на орбите в области WSB, по меньшей мере,одного маневра летательным аппаратом посредством изменения его скорости с обеспечением схода его с орбиты в области WSB,в) осуществление второго перехода летательного аппарата от области WSB или схода его с орбиты в области WSB, по меньшей мере,ко второму небесному телу, либо на орбиту ко второму небесному телу, либо на другую орбиту к первому небесному телу. 2. Способ по п.1, отличающийся тем, что первый переход предусматривает использование, по меньшей мере, операционного баллистического захвата (ВСТ) и хомановского перехода. 3. Способ по п.1 или 2, отличающийся тем,что второй переход предусматривает использование, по меньшей мере, операционного баллистического схода с орбиты (BET) и хомановского перехода. 4. Способ по пп.1-3, отличающийся тем,что первый переход предусматривает использование операционного баллистического захвата(ВСТ), причем операция перемещения (а) дополнительно включает в себя операцию перелета с использованием захвата (ВСТ) от первого небесного тела или с орбиты первого небесного тела, до обеспечения слабого захвата в указанной области слабой устойчивости (WSB) или на орбите в указанной области (WSB), связанной с первым небесным телом, за счет внедрения процесса позиционирования вперед путем изменения параметров до обеспечения сходимости заданных переменных в области (WSB) или на орбите в области (WSB). 5. Способ по пп.1-3, отличающийся тем,что первый переход предусматривает использование операционного баллистического захвата(ВСТ), причем операция перемещения (а) дополнительно включает в себя операцию перелета с использованием захвата (ВСТ) от первого небесного тела или с орбиты первого небесного тела до обеспечения слабого захвата в области слабой устойчивости (WSB) или на орбите в указанной области (WSB), связанной с первым небесным телом, за счет внедрения процесса 52 позиционирования вперед путем изменения, по меньшей мере, двух сферических параметров,до обеспечения сходимости заданных переменных в области (WSB) или на орбите в области(WSB) при сохранении, главным образом, фиксированной, по меньшей мере, одной классической переменной, использованной в процессе позиционирования вперед. 6. Способ по пп.1-3, отличающийся тем,что первый переход предусматривает использование операционного баллистического захвата(ВСТ), причем операция перемещения (а) дополнительно включает в себя операцию перелета с использованием захвата (ВСТ) от первого небесного тела или с орбиты первого небесного тела до обеспечения слабого захвата в области слабой устойчивости (WSB) или на орбите в указанной области (WSB), связанной с первым небесным телом, за счет внедрения процесса позиционирования вперед путем изменения значения скорости VE и угла наклона траектории полета E для обеспечения сходимости заданных переменных в указанной области (WSB) или на орбите в области (WSB), причем заданные переменные включают в себя радиальное расстояние rM и наклонение iM. 7. Способ по пп.1-3, отличающийся тем,что первый переход предусматривает использование операционного баллистического захвата(ВСТ), причем операция перемещения (а) дополнительно включает в себя операцию перелета с использованием первого перехода от первого небесного тела или с орбиты первого небесного тела до обеспечения слабого захвата в области слабой устойчивости (WSB) или на орбите в указанной области (WSB), связанной с первым небесным телом, за счет внедрения процесса позиционирования вперед, который включает в себя ньютоновский алгоритм второго порядка,причем в ньютоновском алгоритме второго порядка используют две переменные управления,включающие в себя значение скорости VE и угол наклона траектории полета E, которые изменяют для достижения условий указанной области (WSB) у второго небесного тела или на орбите второго небесного тела, с использованием двух заданных переменных, в том числе радиального расстояния rM и наклонения iM. 8. Способ по п.7, отличающийся тем, что значение скорости VE и угол наклона траектории полета E развязаны от второго небесного тела или от орбиты второго небесного тела при первом переходе. 9. Способ по п.7, отличающийся тем, что значение скорости VE и угол наклона траектории полета E развязаны от угловых элементов первого небесного тела, в том числе от наклонения iE, восходящего узла относительно ЗемлиE и аргумента периапсиды относительно первого небесного тела E. 53 10. Способ по одному из пп.1-9, отличающийся тем, что операция (b) дополнительно включает в себя проведение маневра с параметрами 2-20 м/с в указанной области (WSB) или на орбите в области (WSB) для выхода из указанной области или для схода с орбиты. 11. Способ по одному из пп.1-10, отличающийся тем, что операция (а) дополнительно включает в себя проведение маневра вокруг второго небесного тела или на орбите второго небесного тела за счет проведения другого маневра с параметрами 2-20 м/с в области (WSB) или на орбите в области (WSB). 12. Способ по одному из пп.1-11, отличающийся тем, что указанная область (WSB) или орбита в указанной области (WSB) являются нелинейными и находятся, главным образом,на границе захвата и ухода, в результате чего возможен как захват, так и уход при, главным образом, нулевом или относительно малом маневре, причем гравитационные возмущения солнца оказывают воздействие как на первый,так и на второй переходы. 13. Способ по одному из пп.1-12, отличающийся тем, что указанная область (WSB) или орбита в указанной области (WSB) находятся главным образом на границе взаимодействия между гравитационными полями первого небесного тела и второго небесного тела. 14. Способ по одному из пп.1-13, отличающийся тем, что, по меньшей мере, космический корабль, спутник или ракета входят, по меньшей мере, в указанную область (WSB) или переходят на орбиту в области (WSB) таким образом, что кеплеровская энергия, по меньшей мере, космического корабля, спутника или ракеты является слегка отрицательной близкой к нулю. 15. Способ по одному из пп.1-14, отличающийся тем, что, по меньшей мере, только указанная область (WSB) или орбита в указанной области (WSB) реализованы на заранее определенной случайной высоте путем задания заранее определенного значения скорости, по меньшей мере, космического корабля, спутника или ракеты, в результате чего определен заданный эксцентриситет захвата. 16. Способ по одному из пп.1-15, отличающийся тем, что операция (а) дополнительно включает в себя проведение маневра вокруг второго небесного тела или на орбите второго небесного тела за счет проведения другого маневра с параметрами 2-20 м/с в указанной области (WSB) или на орбите в указанной области(WSB), по меньшей мере, только при синхронизации и при позиционировании, по меньшей мере, космического корабля, спутника или ракеты ранее выхода из указанной области (WSB) или схода с орбиты в указанной области (WSB). 17. Способ по одному из пп.1-16, отличающийся тем, что второй переход предусматривает использование операционного баллисти 002665 54 ческого схода с орбиты (BET), причем операция перемещения (с) дополнительно включает в себя перелет с использованием схода с орбиты(ВСТ) от состояния слабого захвата в области слабой устойчивости (WSB) или на орбите в указанной области (WSB), по меньшей мере,только к первому небесному телу, или на орбиту первого небесного тела, или ко второму небесному телу, или на орбиту второго небесного тела за счет внедрения процесса позиционирования вперед путем изменения вторых параметров способа до обеспечения сходимости вторых заданных параметров в указанной области(WSB) или на орбите в указанной области(WSB). 18. Способ по п.17, отличающийся тем, что вторые заданные переменные развязаны, по меньшей мере, от первого небесного тела или от орбиты первого небесного тела и от угловых элементов второго небесного тела. 19. Способ по одному из пп.1-18, отличающийся тем, что в качестве первого небесного тела или орбиты первого небесного тела используют Землю или околоземную орбиту, а в качестве второго небесного тела или орбиты второго небесного тела используют Луну или окололунную орбиту. 20. Способ по п.1, отличающийся тем, что для обеспечения перехода космического летательного аппарата от первого небесного тела или с орбиты первого небесного объекта ко второму небесному телу или на орбиту второго небесного тела осуществляют независимые стадии(a) ввода параметров способа генерирования операционного баллистического захвата для перехода;(b) осуществления процесса позиционирования вперед, изменяя при этом параметры для сходимости заданных переменных второго небесного тела или на орбите второго небесного тела от первого небесного тела или от орбиты первого небесного тела; и(c) повторения стадии (b) до достижения достаточной сходимости, получение операционного баллистического захвата для перехода от первого небесного тела или орбиты первого небесного тела ко второму небесному телу или на орбиту второго небесного тела. 21. Способ по п.20, отличающийся тем, что стадия повторения (с) дополнительно включает стадию повторения (b) до достижения достаточной сходимости, чтобы получить операционный баллистический захват для перехода от первого небесного тела или сходя с орбиты первого небесного тела ко второму небесному телу или на орбиту второго небесного тела через область слабой устойчивости (WSB) на орбите между ними. 22. Способ по п.20 или 21, отличающийся тем, что стадия осуществления процесса (b) дополнительно включает стадию внедрения про 55 цесса позиционирования вперед, изменяя, по меньшей мере, два сферических параметра для сходимости заданных переменных у второго небесного тела или на орбите второго небесного тела при поддержании постоянства, по меньшей мере, одной классической переменной, используемой в указанном процессе позиционирования вперед. 23. Способ по п.20 или 21, отличающийся тем, что стадия осуществления процесса (b) дополнительно включает стадию процесса позиционирования вперед при изменении величины скорости VE и угла наклона траектории полетаE для сходимости заданных переменных у второго небесного тела или на орбите второго небесного тела, причем заданные переменные включают радиальное расстояние rM и наклонение iM. 24. Способ по п.20 или 21, отличающийся тем, что стадия осуществления процесса (b) дополнительно включает стадию процесса позиционирования вперед, включающую ньютоновский алгоритм второго порядка, причем в ньютоновском алгоритме второго порядка используют две переменные управления, включая величину скорости VE и угол наклона траектории полета E, которые изменяют для достижения условий захвата у второго небесного тела или на орбите второго небесного тела, используя две заданные переменные, включая радиальное расстояние rM и наклонение iM. 25. Способ по п.23 или 24, отличающийся тем, что величина скорости VE и угол наклона траектории полета E развязаны от второго небесного тела или от орбиты второго небесного тела при осуществлении операционного баллистического захвата для перехода. 26. Способ по п.23 или 24, отличающийся тем, что величина скорости VE и угол наклона траектории полета E развязаны от угловых элементов первого небесного тела, в том числе от наклонения iE, восходящего узла относительно Земли WE и аргумента периапсиды относительно первого небесного тела wE. 27. Способ по любому из пп.20 или 26, отличающийся тем, что стадия процесса (b) дополнительно включает стадию генерирования траектории вокруг второго небесного тела или орбиты второго небесного тела, включая выполнение незначительного маневра с параметрами 2-20 м/с в области слабой устойчивости(WSB) или на орбите (WSB), связанной со вторым небесным телом. 28. Способ по п.27, отличающийся тем, что область (WSB) или орбиту в области (WSB) определяют как нелинейную, находящуюся, в основном, на границе захвата и ухода, в результате чего возможен как захват, так и уход при существенно нулевом или относительно малом маневре, при этом гравитационные возмущения 56 Солнца оказывают воздействие, как на первый,так и на второй переходы. 29. Способ по п.27 или 28, отличающийся тем, что область (WSB) или орбиту в указанной области (WSB) определяют, в основном, на границе взаимодействия между гравитационными полями первого небесного тела и второго небесного тела. 30. Способ по п.27, 28 или 29, отличающийся тем, что, по меньшей мере, космический корабль, спутник или ракета входят, по меньшей мере, в область (WSB) или переходят на орбиту в области (WSB) таким образом, что кеплеровская энергия, по меньшей мере, космического корабля, спутника или ракеты является слегка отрицательной и, в основном, близкой к нулю. 31. Способ по любому из пп.27-30, отличающийся тем, что, по меньшей мере, область(WSB) или орбита в указанной области (WSB) реализованы на заранее определенной случайной высоте путем задания заранее определенного значения скорости, по меньшей мере, космического корабля, спутника или ракеты, в результате чего определен заданный эксцентриситет захвата. 32. Способ по любому из пп.21-31, отличающийся тем, что стадия осуществления процесса (b) дополнительно включает стадию проведения маневра вокруг второго небесного тела или на орбите второго небесного тела за счет проведения другого маневра с параметрами 2-20 м/с в области (WSB) или на орбите в области(WSB), по меньшей мере, при синхронизации и при позиционировании, по меньшей мере, космического корабля, спутника или ракеты до выхода из области (WSB) или схода с орбиты в области (WSB). 33. Способ по любому из пп.21-32, отличающийся тем, что процесс позиционирования вперед предусматривает использование ньютоновского алгоритма второго порядка. 34. Способ по любому из пп.23-26, отличающийся тем, что дополнительно включает следующие стадии:(e) преобразование классических элементов в сферические координаты, в котором сферические координаты включают преобразованные величины VE, E, а также долготу E, широту E, азимут/угол траектории полета с измененной вертикалью E. 35. Способ по любому из пп. 21-34, отличающийся тем, что в качестве первого небесного тела или орбиты первого небесного тела используют Землю или околоземную орбиту, а в качестве второго небесного тела или орбиты второго небесного тела используют Луну или окололунную орбиту.
МПК / Метки
МПК: B64G 1/10, G06F 17/00
Метки: орбиты, области, высоты, способ, границ, летательного, космического, малой, наклонения, использованием, изменения, устойчивости, аппарата
Код ссылки
<a href="https://eas.patents.su/30-2665-sposob-izmeneniya-nakloneniya-i-vysoty-orbity-kosmicheskogo-letatelnogo-apparata-s-ispolzovaniem-granic-oblasti-malojj-ustojjchivosti.html" rel="bookmark" title="База патентов Евразийского Союза">Способ изменения наклонения и высоты орбиты космического летательного аппарата с использованием границ области малой устойчивости</a>
Предыдущий патент: Концентрированные растворы лейкоиндиго
Следующий патент: Вспомогательный модуль индикации для электрической коммутационной аппаратуры с расцепителем
Случайный патент: Гетеродимерные связывающие белки и их применение












