Моделирование, имитация и сравнение моделей формирования червоточины при моделировании режима интенсификации добычи из карбонатной матрицы

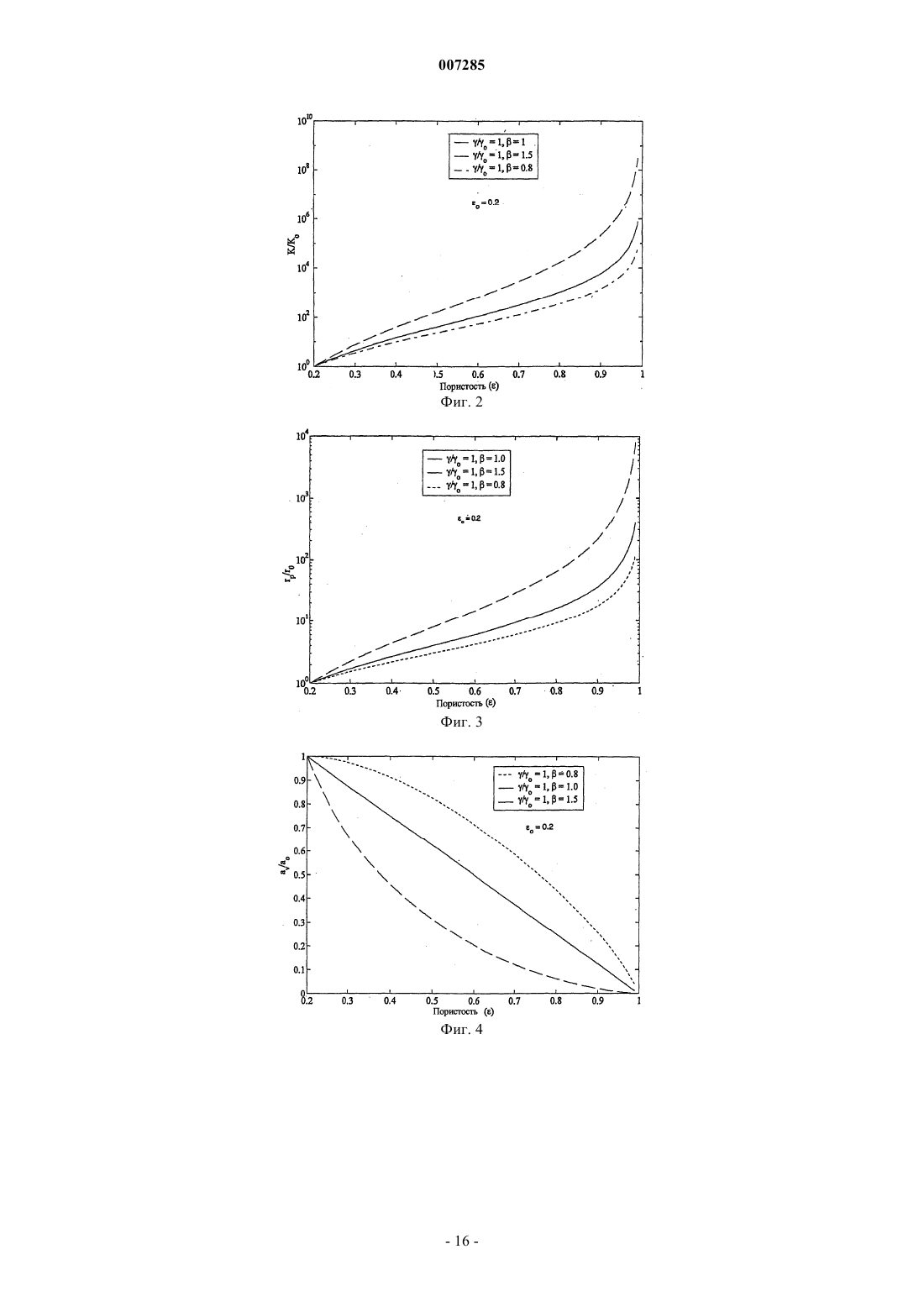
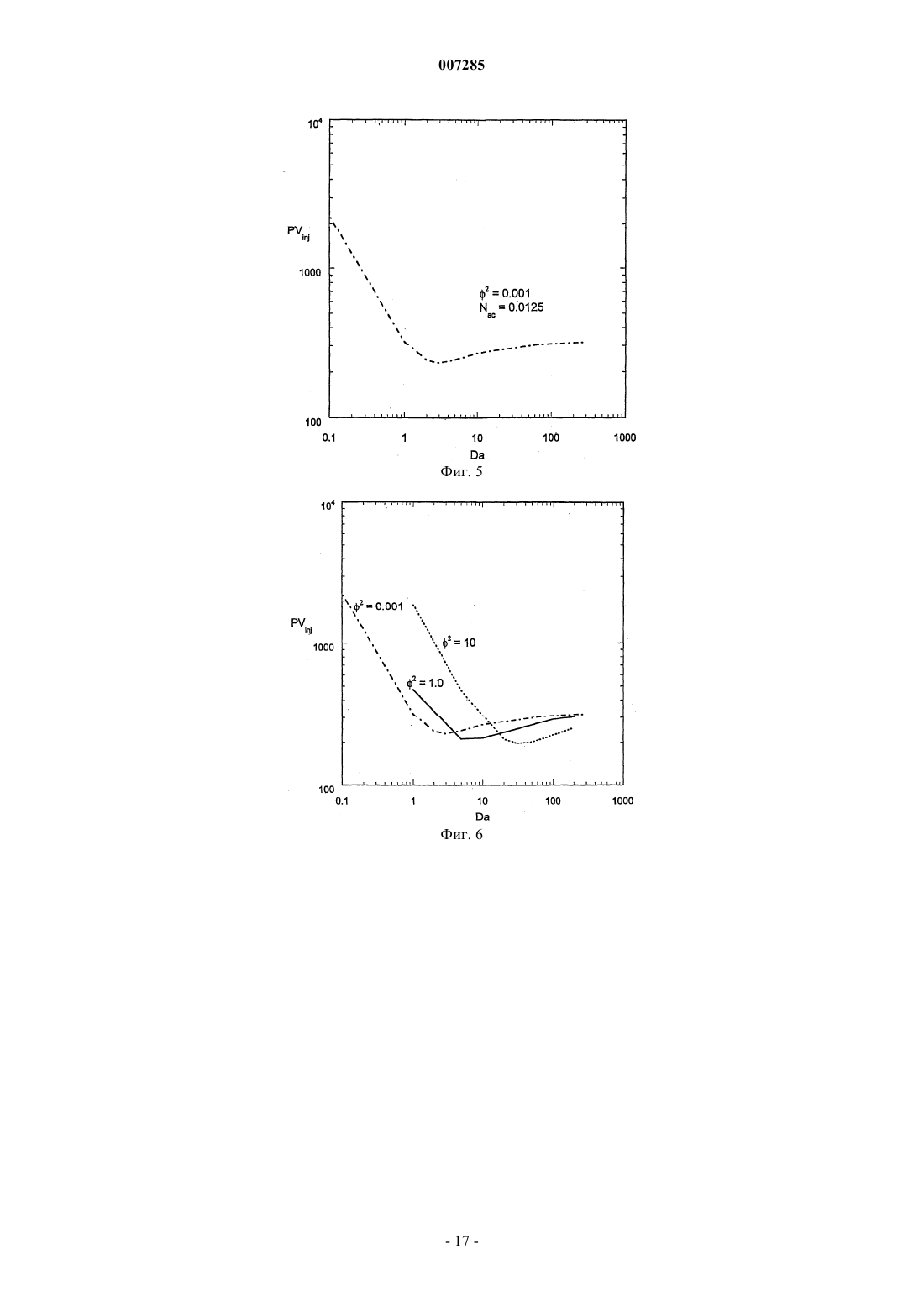
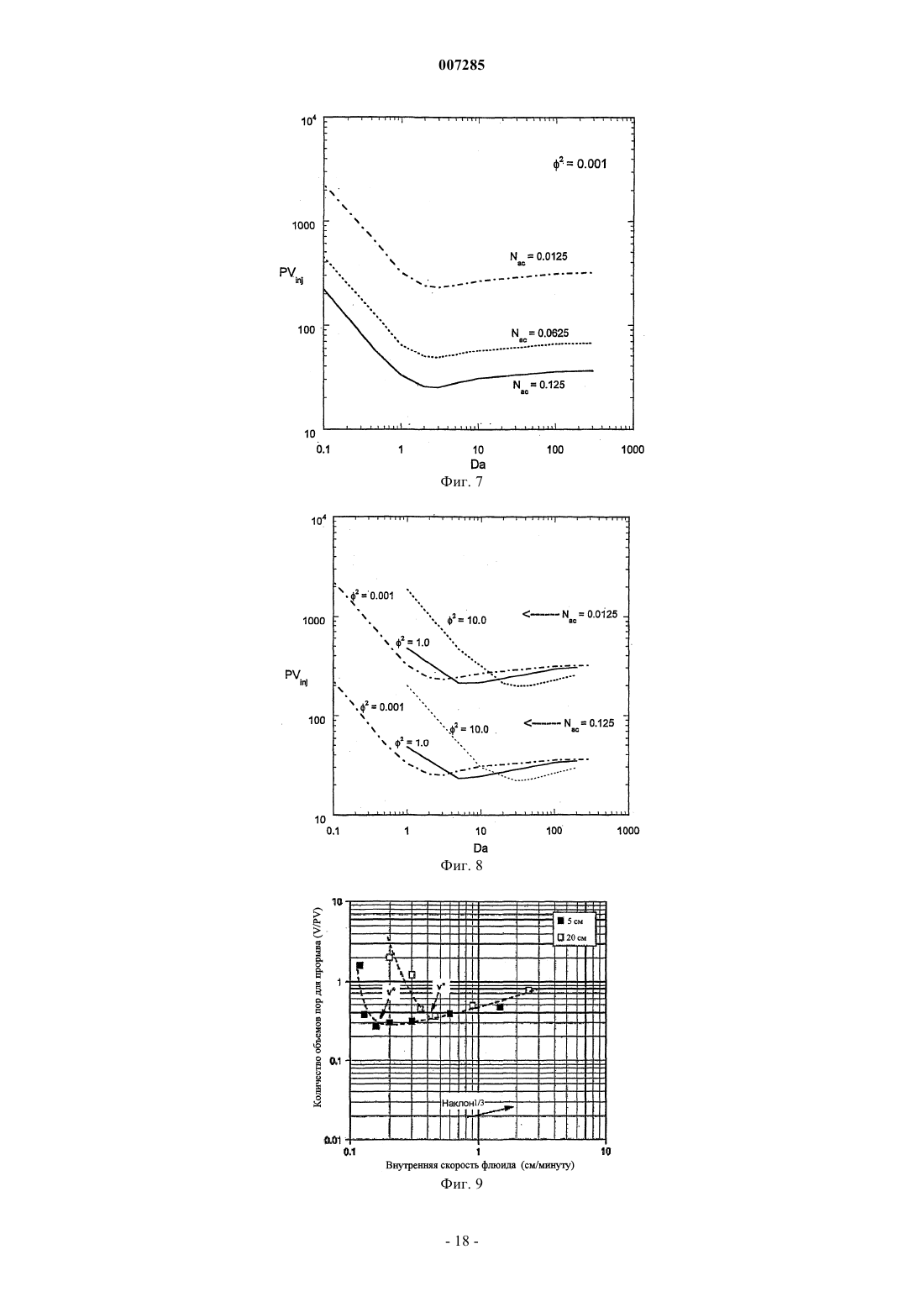
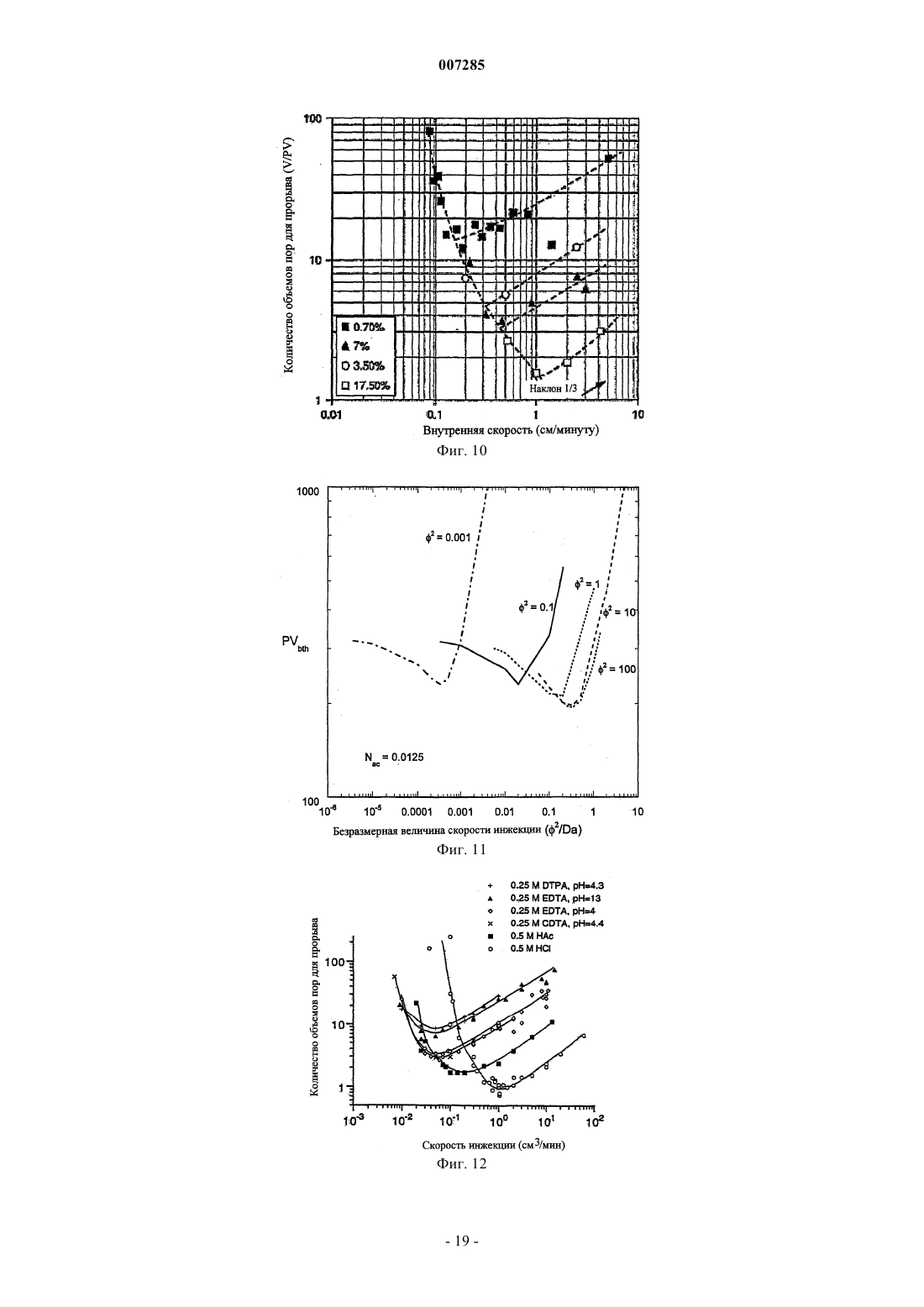
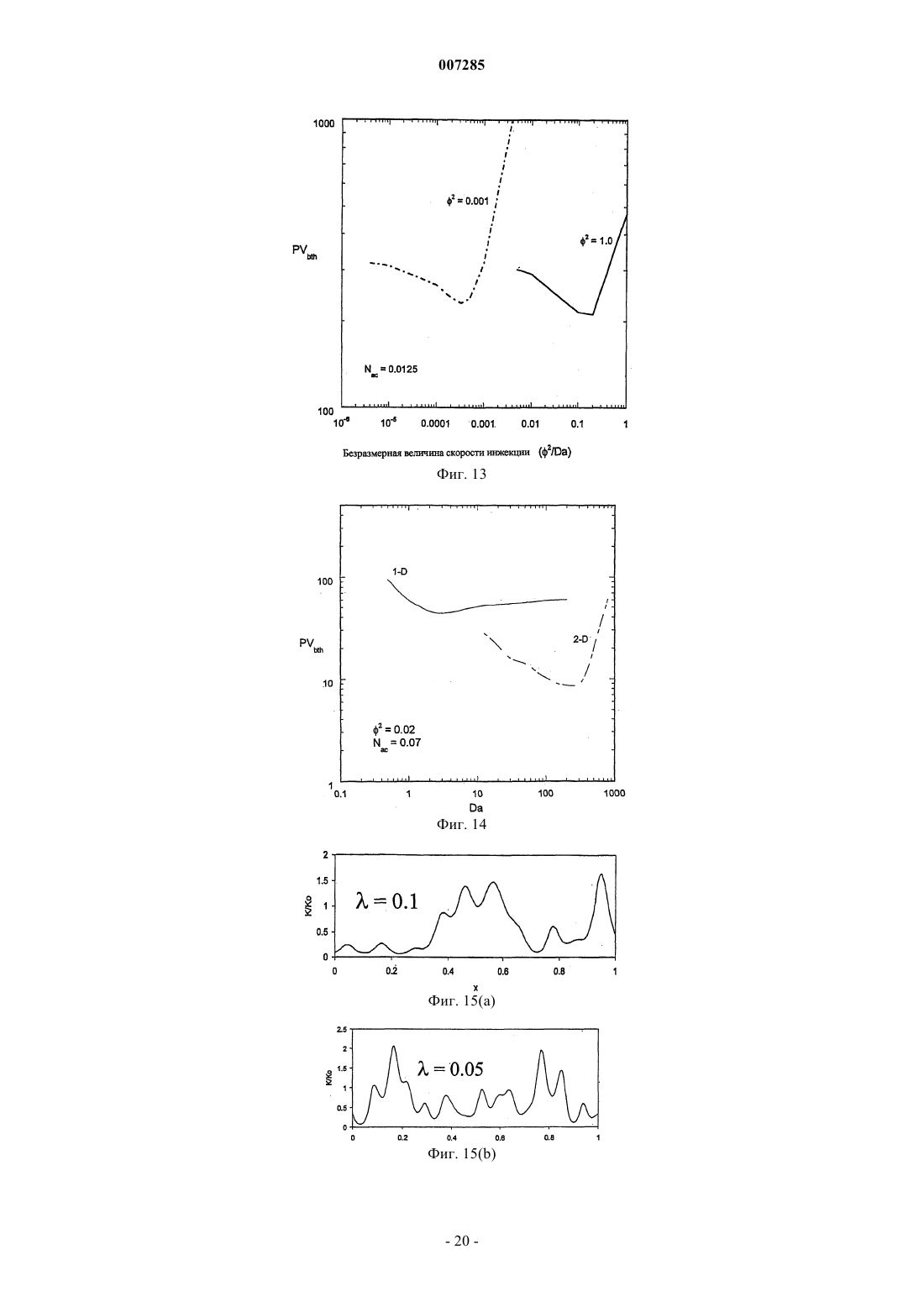
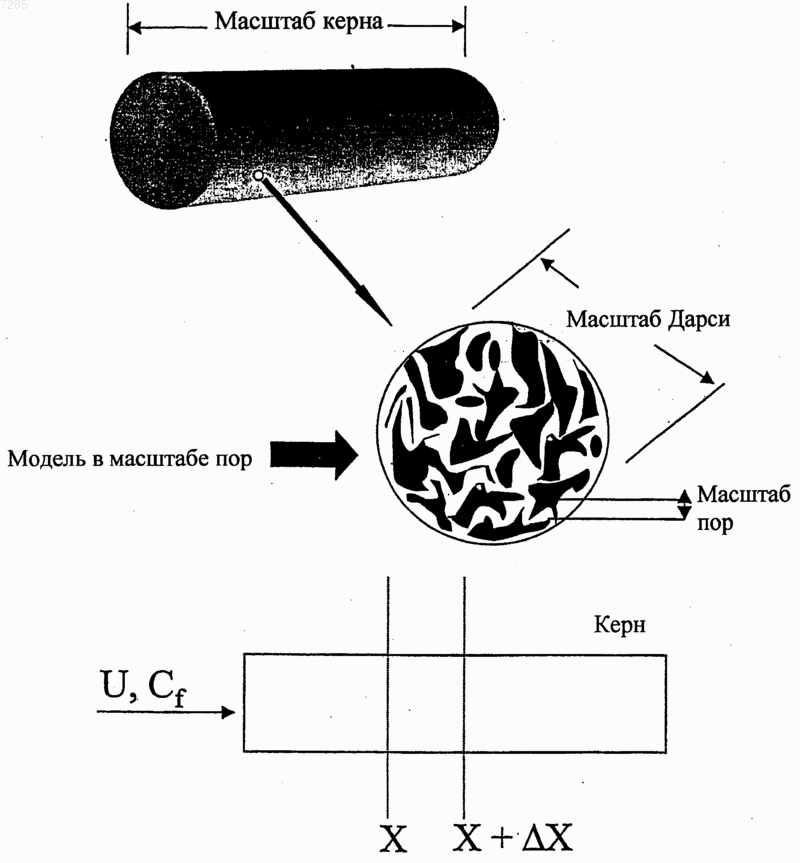
007285 Ссылка на родственные заявки В настоящей заявке заявлен приоритет предварительной заявки на патент США регистрационный 60/384,957. Предпосылки изобретения Область техники Настоящее изобретение, в общем, относится к интенсификации добычи углеводородов в скважине и, в частности, направлено на способ расчета параметров обработки матрицы. Настоящее изобретение, в частности, используется для расчета параметров кислотной обработки в карбонатных месторождениях. Предшествующий уровень техники Кислотная обработка матрицы представляет собой широко используемую технологию интенсификации добычи из скважины. Первичная цель этого процесса состоит в снижении сопротивления потоку пластовых флюидов, вызванного естественной плотностью формации или повреждениями. Кислота растворяет материал матрицы и создает каналы для потока, которые повышают проницаемость матрицы. Эффективность этого процесса зависит от типа используемой кислоты, условий подачи, структуры среды, переноса массы из жидкости в твердое вещество, скорости реакции и т.д. Хотя растворение повышает проницаемость, относительное повышение проницаемости для заданного количества кислоты, как считается, находится в строгой функциональной зависимости от условий инжекции кислоты. В пластах песчаника проявляется тенденция формирования равномерного фронта реакции, и при этом не наблюдается образование каналов потока. В карбонатных пластах в зависимости от условий инжекции может быть получено множество структур растворения, которые изменяются от равномерного до конического типа и типа червоточины. При очень низких скоростях потока кислота быстро расходуется после контакта со средой, в результате чего происходит быстрое растворение. При этом при высоких скоростях потока наблюдаются более равномерные структуры растворения. При промежуточных скоростях потока формируются длинные проводящие каналы, известные, как червоточины. Эти каналы проходят глубоко в формацию и способствуют образования потока нефти. Эксперименты, проведенные в карбонатных кернах, показали, что при заданном количестве инжектируемой кислоты в червоточинах наблюдается более высокое относительное повышение проницаемости. Таким образом, для оптимизации обработки для интенсификации добычи предпочтительно идентифицировать параметры (например, скорость инжекции, тип кислоты, толщину и проницаемость поврежденной зоны и т.д.), которые обеспечивают формирование червоточин с оптимальной плотностью и глубиной проникновения в продуктивный пласт. Хорошо известно, что оптимальная скорость инжекции зависит от скорости реакции и диффузии разных видов кислоты, концентрации кислоты, длины образца керна, температуры, проницаемости среды и т.д. Влияние вышеуказанных факторов на формирование формации типа червоточины изучают экспериментально. Несколько теоретических исследований было проведено в прошлом для получения оценки оптимальной скорости инжекции и для понимания явления канализации потока, связанной с реакционным растворением в пористых средах. Однако существующие модели описывают только несколько аспектов процесса кислотной обработки и соединение механизмов реакции и переноса в различных масштабах, которые играют ключевую роль при оценке оптимальной скорости инжекции, неправильно учитывается в этих моделях. Были предложены несколько моделей, которые основаны на предположении существования червоточины. При этом можно сделать ссылку, например, на публикации Wang, Y., Hill, A.D., and Schechter,R.S. "The Optimum Injection Rate for Matrix Acidizing of Carbonate Formations," paper SPE 26578 presentedFormation Damage Conference held in The Hague, 31 May-01 June, 1999. Эти модели используют для изучения влияния утечки жидкости, кинетики реакции и т.д., на скорость распространения червоточины и влияния соседних червоточин на скорость роста доминирующей червоточины. Простая структура этих моделей является преимуществом подробного изучения реакции,механизмов диффузии и конвекции внутри червоточины. Эти модели, однако, нельзя использовать для изучения инициирования червоточины и влияния неоднородностей на формирование червоточины. Сетевые модели, описывающие реакционное растворение, были представлены в публикацияхWormhole Formation in Porous Media" AIChE J, 44, 1933-1949 (1998). Эти модели представляют пористую среду как сеть трубок, взаимосвязанных друг с другом в узлах. Поток кислоты внутри этих трубок описан с использованием взаимозависимости Хагена-Пуазейля для ламинарного потока в трубе. Кислота вступает в реакцию с материалом стенки трубки, и растворение происходит при увеличении радиуса трубки. Сетевые модели позволяют прогнозировать структуру растворения и качественные характеристики растворения, такие как оптимальная скорость потока, наблюдаемая в экспериментах. Однако мо-1 007285 делирование в масштабе керна с использованием сетевой модели требует применения значительной вычислительной мощности, и включение в эти модели влияния слияния пор и неоднородностей трудновыполнимо. Результаты, полученные с использованием сетевых моделей, также имеют проблемы, связанные с масштабированием. Промежуточный подход при описании реакционного растворения включает использование усредненных моделей или моделей сплошных сред. Усредненные модели использовались для описания растворения карбонатов авторами Pomes, V., Bazin, В., Golfier, F., Zarcone, С, Lenormand, R. and Quintard,M.: "On the Use of Upscaling Methods to Describe Acid Injection in Carbonates," paper SPE 71511 presented at 2001 SPE Annual Technical Conference and Exhibition held in New Orleans, Lousiana, 30 September - 3Fluid Mech., 457, 213-254 (2002). В отличие от сетевых моделей, которые описывают растворение в масштабе поры и моделей, основанных на предположении существования червоточин, усредненные модели описывают растворение в масштабе, намного большем, чем масштаб поры, и в масштабе, намного меньшем, чем масштаб керна. Такой промежуточный масштаб также известен как масштаб Дарси. Усредненные модели позволяют обойти проблемы масштабирования, связанные с сетевыми моделями, позволяют предсказать инициирование, распространение червоточины, и их можно использовать для изучения влияния неоднородностей в среде на процесс растворения. Результаты, полученные на основе усредненных моделей, могут быть расширены на масштаб, используемый в процессе эксплуатации. Успех этих моделей зависит от вводимых ключевых данных, таких как скорость переноса массы, корреляция проницаемости-пористости и т.д., которые зависят от процессов, происходящих в масштабе пор. Для усредненной модели, написанной в масштабе Дарси, требуется вводить эти данные в масштабе поры. Поскольку структура пористой среды развивается со временем, вычисления на уровне пор должны быть выполнены на каждом этапе для получения входных данных для усредненного уравнения. Усредненные уравнения, используемые авторами Golfier и др., а также Pomes др., описывают перенос реагента на уровне масштаба Дарси с использованием псевдогомогенной модели, т.е. в них используется простая переменная концентрации. Кроме того, в них предполагается, что реакция управляется переносом массы (т.е. концентрация реагента на поверхности раздела твердое вещество-жидкость равна нулю). Авторы настоящей заявки определили, что большинство систем можно отнести к диапазону между режимами переноса масс и кинетически управляемыми режимами реакции, когда использование псевдогомогенной модели (одной переменной концентрации) не достаточно для получения всех качественных свойств процесса реакционного растворения и что "априорное" предположение, что система находится в режиме с управляемым переносом масс, часто используемое в литературе, может не иметь отношения к качественным свойствам проблемы. Поэтому было бы предпочтительно получить улучшенную модель, направленную на прогнозирование структуры растворения при интенсификации добычи из карбонатной матрицы. Сущность изобретения В настоящем изобретении предложено моделировать обработку для интенсификации добычи,включающую проведение химической реакции в пористой среде, включая описание химической реакции путем соединения реакций и переноса масс, происходящих на уровне масштаба Дарси, и на уровне масштаба пор, и с учетом концентрации Cf реагента в фазе флюидов поры, а также концентрации указанного реагента Cs на поверхности раздела межу жидким и твердым веществом поры. Настоящее изобретение в особенности пригодно для моделирования кислотной обработки подземной формации, в частности кислотной обработки матрицы и кислотного образования трещин. Не говоря уже об интенсификации добычи в скважине, проблема реакции и переноса в пористых средах также проявляется в плотных слоях, при переносе загрязнителя в грунтовых водах, распределении трейсера и т.д. Присутствие шкал различной длины и связь между процессами, происходящими в различном масштабе,представляет собой общую характеристику, которая является существенной проблемой при моделировании этих систем. Например, структура растворения, наблюдаемая в масштабе керна, представляет собой результат реакции и диффузионных процессов, происходящих внутри пор, которые имеют микроскопические размеры. Для определения крупномасштабных свойств важно обеспечить эффективный перенос информации по процессам на уровне масштаба пор в масштаб с большей размерностью. Кроме связи между масштабами различной размерности, изменение в структуре среды добавляет дополнительный параметр, повышающий сложность систем моделирования, направленных на использование растворения. Модель в соответствии с настоящим изобретением улучшает усредненные модели путем учета того факта, что в ходе реакции может одновременно происходить перенос массы, и реакция при этом может быть кинетически регулируемой, что, в частности, происходит в случае, когда используют относительно медленно реагирующие химикаты, такие как хеланты, при одновременном учете возможности пространственного изменения структуры пор может в области, например, из-за неоднородностей и растворения.-2 007285 В соответствии с другим вариантом выполнения настоящего изобретения учитывают как асимптотно/диффузивный, так и конвекционный вклад в коэффициент локального переноса массы. Это позволяет прогнозировать переходы между различными режимами реакции. Краткое описание чертежей На фиг. 1 показана схема, представляющая масштабы с различной размерностью в пористой среде; на фиг. 2 показан график зависимости проницаемости от пористости для различных значений эмпирического параметра , используемого в уравнении (7); на фиг. 3 показан график, изображающий увеличение радиуса пор с пористостью, как функция ; на фиг. 4 показан график, представляющий снижение граничной площади с пористостью, как функция ; на фиг. 5 показан график, представляющий количество объемов пор, требуемых для прорыва, рассчитанное с использованием 1-D модели в зависимости от числа Дамкелера для 2=0,001 и Nac=0,0125; на фиг. 6 показан график, представляющий зависимость оптимального числа Дамкелера от модуля Тиле 2; на фиг. 7 показан график, представляющий зависимость количества объемов пор, требуемых для прорыва, от числа Nac расхода кислоты; на фиг. 8 показан график, изображающий зависимость количества объемов пор, требуемых для прорыва, и оптимального числа Дамкелера от параметров 2 и Nac; на фиг. 9 показан экспериментальный график количества объемов пор, требуемых для прорыва, в зависимости от скорости инжекции для различной длины керна; на фиг. 10 показан экспериментально полученный график, представляющий снижение оптимального количества объемов пор, требуемых для прорыва, при повышении концентрации кислоты; на фиг. 11 показаны результаты моделирования с использованием 1-D модели, в соответствии с настоящим изобретением, иллюстрирующие сдвиг оптимальной скорости инжекции при повышении модуля Тиле 2; на фиг. 12 показан экспериментальный график зависимости количества объемов пор, требуемых для прорыва, от скорости инжекции для различных кислот; на фиг. 13 представлено повышение оптимальной скорости инжекции, спрогнозированной с помощью 1-D модели, в соответствии с настоящим изобретением, с увеличением модуля Тиле 2; на фиг. 14 показан график, представляющий прогнозирование, с использованием 1-D и 2-D моделей, оптимального количества объемов пор, требуемых для прорыва. При использовании 2-D модели получено гораздо меньшее количество объемов пор, требуемых для прорыва, из-за эффекта образования каналов; на фиг. 15 показаны коррелированные поля случайной проницаемости для различных длинкорреляции, сгенерированных на области единичной длины, с использованием экспоненциальной ковариационной функции. Двухшкальная модель сплошной среды Конвекция и диффузия кислоты, а также реакция на твердой поверхности, представляет собой основные механизмы, которые управляют процессом растворения. Эффекты конвекции являются важными в масштабе длины, гораздо большем, чем шкала Дарси (например, в масштабе длины керна), в то время,как диффузия и реакция представляют собой основные механизмы в масштабе пор. Хотя зависимости конвекции проявляются при большей длине шкалы, диффузия и реакция представляют собой локальные по своей природе явления, т.е. они зависят от локальной структуры пор и локальных гидродинамических свойств. Явление реакционного растворения моделируют как связь между процессами, происходящими в этих двух масштабах, а именно в масштабе Дарси и в масштабе пор, как показано на фиг. 1. Двухшкальная модель реакционного растворения описывается с помощью уравнений (1-5). Здесь U=(U, V, W) представляет вектор скорости Дарси, K представляет тензор проницаемости, Р представляет давление,представляет пористость, Cf представляет концентрацию кислоты в фазе флюидов, при которой происходит смешение лунок, Cs представляет концентрацию кислоты на границе раздела жидкость-твердое вещество, De представляет эффективный тензор дисперсии, kс представляет коэффициент локального переноса масс, av представляет межфазную поверхность, доступную для реакции на-3 007285 единицу объема среды, ps представляет плотность твердой фазы ипредставляет растворяющую силу кислоты, определяемую, в граммах растворяемого твердого вещества на моль вступившей в реакцию кислоты. Кинетика реакции представлена R(Cs). Для реакции первого порядка R(Cs) сводится к ksCs, гдеks представляет собой постоянную поверхностной скорости реакции, которая имеет размерность, представленную в единицах скорости. Уравнение (3) задает описание в масштабе Дарси переноса кислоты. Первые три члена уравнения представляют накопление, конвекцию и дисперсию кислоты соответственно. Четвертый член описывает перенос кислоты из жидкой фазы на границу раздела жидкость-твердое вещество, и его роль более подробно описана ниже в данном разделе настоящего описания. Поле U скорости в элементе конвекции получают из закона Дарси (уравнение 1), который связывает скорость с полем К проницаемости и градиентом давления. Закон Дарси обеспечивает хорошую оценку поля потока при низком значении числа Рейнольдса. Для потоков с числом Рейнольдса больше, чем единица, для описания поля потока можно использовать формулу Дарси-Бринкмана, которая включает вклад вязкости в поток. Хотя скорости потока,представляющие здесь интерес, имеют число Рейнольдса меньше чем единица, изменение в поле проницаемости из-за растворения может сделать число Рейнольдса больше единицы. Однако при выполнении расчетов для настоящего изобретения предпочтительно используют закон Дарси, который является менее громоздким, чем формула Дарси-Бринкмана, хотя модель может быть легко расширена до формулировки Бринкмана. Первый член континуума в уравнении (2) учитывает влияние локального изменения объема в ходе растворения на поле потока. При выводе уравнения континуума предполагается, что процесс растворения несущественно изменяет плотность жидкой фазы. Член переноса в балансе видов веществ в уравнении (3) описывает истощение реагента в масштабе Дарси в ходе реакции. Точная оценка этого члена зависит от описания механизмов переноса и реакции внутри пор. Следовательно, для расчета члена переноса в уравнении (3) требуются расчет в масштабе пор переноса кислоты на поверхность пор и реакции на поверхности. В отсутствие реакции, концентрация кислоты внутри пор будет равномерной. Реакция на границе раздела между твердым и жидким веществом приводит к повышению градиента концентрации в жидкой фазе внутри пор. Величина этого градиента зависит от относительной скорости переноса массы из жидкой фазы на границу раздела жидкость-твердое вещество и скорости реакции на этой границе раздела. Если скорость реакции будет очень мала по сравнению со скоростью переноса массы, градиент концентрации будет незначительным. В этом случае считается, что реакция происходит в кинетически управляемом режиме, и одиночная переменная концентрации достаточна для описания этой ситуации. Однако если скорость реакции очень высока по сравнению со скоростью переноса массы, внутри пор развиваются крутые градиенты. Этот режим реакции известен как режим, управляемый переносом массы. Для учета градиентов, развивающихся в результате режимов, управляемых переносом массы, требуется получить решение дифференциального уравнения, описывающего механизмы диффузии и реакции внутри каждой поры. Поскольку это непрактично,авторы использовали две переменные Cs и Cf концентрации, одну для концентрации кислоты на границе раздела жидкость-твердое вещество и другую - для концентрации в жидкой фазе соответственно, и получаем информацию о градиентах концентрации, как разность между этими двумя переменными, с использованием концепции коэффициента переноса массы. Математическое представление идеи переноса между жидкой фазой и границей раздела жидкостьтвердое вещество с использованием двух переменных концентрации и реакции на границе перехода показано в уравнении (4). Левая сторона этого уравнения представляет перенос между фазами с использованием разности между переменными концентрации и коэффициентом kс переноса массы. Количество реагента, перенесенного на поверхность, приравнивают к количеству реагента, вступившего в реакцию. Для случая кинетики первого порядка (R(Cs)=ksCs) уравнение (4) может быть упрощено и сведено к следующему виду: В кинетически управляемом режиме отношение ks/kc очень мало, и концентрация на границе раздела жидкость-твердое вещество приблизительно равна концентрации жидкой фазы (CsCf). В режиме,управляемом переносом массы, отношение ks/kc очень велико. В этом режиме значение концентрации на границе раздела жидкость-твердое вещество (уравнение (6 очень мало (Cs0). Поскольку постоянная скорости для заданной кислоты является фиксированной, величина отношения ks/kc определяется по локальному коэффициенту kс переноса массы. Коэффициент переноса массы представляет собой функцию размера пор и локальной гидродинамики. Из-за растворения и неоднородностей в среде размер пор и скорость жидкости являются одновременно функциями положения и времени. Таким образом, отношение ks/kc не является постоянным в среде, а изменяется в зависимости от пространства и времени, что приводит к ситуации, когда в различных местах среды проходят различные режимы реакции. Для описания такой ситуации, по существу, достаточно учитывать как кинетический режим, так и режим, управляемый переносом массы, в модели, которая была получена здесь с использованием двух переменных-4 007285 концентрации. Одиночная переменная концентрации недостаточна для одновременного описания обоих режимов. Двухшкальная модель может быть расширена до случая комплексной кинетики путем ввода соответствующей формы кинетики R(CS) реакции в уравнении (4). Если кинетика является нелинейной, уравнение (4) становится нелинейным алгебраическим уравнением, решение которого должно быть найдено наряду с уравнением баланса различных видов веществ. Для обратимых реакций концентрация продукта влияет на скорость реакции, при этом уравнения баланса дополнительных веществ, описывающие концентрацию продукта, должны быть добавлены для завершения модели при наличии таких реакций. Изменение локальной пористости описано с помощью уравнения развития пористости по уравнению (5). Это уравнение получено путем балансировки количества кислоты, вступившей в реакцию, с соответствующим количеством растворенного твердого вещества. Для завершения модели по уравнениям (1-5), требуется информация о тензоре К проницаемости,тензоре De дисперсии, коэффициенте kс переноса масс и площади границы перехода av. Эти величины зависят от структуры пор и представляют собой данные, вводимые в модель в масштабе Дарси из модели в масштабе пор. Вместо расчета этих величин из подробной модели в масштабе пор, с учетом действительной структуры пор, здесь используют взаимозависимость структура-свойство, которая связывает проницаемость, площадь границ перехода и средний радиус пор в модели в масштабе пор с ее пористостью. Однако может быть выполнен подробный расчет, включая структуру пор, и приведенные выше величины К, De, kc и av, полученные из модели в масштабе пор, могут быть переданы в модель в масштабе Дарси. Здесь используют взаимозависимость структура-свойство для изучения тенденции поведения растворения для различных типов взаимозависимостей структура-свойство и для уменьшения объема расчетов, связанных с подробным расчетом в масштабе пор. Модель в масштабе пор Взаимозависимость структура-свойство Растворение постоянно изменяет структуру пористой матрицы, что затрудняет корреляцию изменения локальной проницаемости с пористостью во время кислотной обработки. Результаты, полученные из усредненных моделей, в которых используют эти корреляции, подвержены количественным ошибкам,возникающим в результате использования плохой корреляции между структурой и свойством среды,хотя прогнозируемые качественные тенденции могут быть правильными. Моделирование на уровне пор,когда свойства рассчитывают на основе указанной структуры среды, устраняет необходимость использования этих корреляций. В отсутствие реакции, когда структура матрицы не изменяется, свойства, прогнозируемые моделями на уровне пор, могут быть репрезентативными в случае реального поля, при условии, что указанная структура является достаточно точной. Однако изменения в структуре, такие как слияние пор, изменяющие координационное число, и т.д., вызванное растворением, трудно внедрить в эти модели, и, следовательно, прогнозы не могут быть точными или репрезентативными, что и наблюдается. Поскольку не существует определенного способа взаимоувязывания изменений свойств среды с изменениями в структуре, здесь используются полуэмпирические взаимоотношения, которые связывают свойства с параметрами (например, с пористостью), которые представляют собой меру структуры среды. Эти взаимозависимости обеспечивают преимущество изучения чувствительности результатов в отношении различных качественных тенденций между структурой и свойствами. Проницаемость среды может быть связана с ее пористостью с использованием взаимозависимости (7), предложенной автором Civan в публикации "Scale effect on Porosity and Permeability: Kinetics, Model and Correlation", AIChE J, 47, 271287(2001). Параметрыипредставляют собой эмпирические параметры, введенные для учета растворения. Для параметрови 1/ наблюдается их увеличение во время растворения и уменьшение при осаждении. В уравнении (7) гидравлический диаметр K/)1/2) связан с отношением объема пор к объему матрицы. Проницаемость, средний радиус пор и площадь поверхности раздела в модели в масштабе пор связаны с их исходными значениями K0, а 0, r0, соответственно в уравнениях (8)-(10). На фиг. 2, 3 и 4 показаны графики проницаемости, радиуса пор и площади поверхности раздела в зависимости от пористости, соответственно, для типичных значений параметров. Увеличение пористости при растворении снижает площадь поверхности раздела, что, в свою очередь, снижает скорость реакции-5 007285 на единицу объема. Уменьшение площади поверхности раздела, которое приводит к увеличению пористости, показано на фиг. 4. Модель могла бы дать лучшие результаты, если бы были бы использованы корреляции структура-свойство, разработанные для конкретной, представляющей интерес системы. Следует отметить, что, в вышеуказанной взаимозависимости проницаемость, т.е. тензор, сведена к скаляру для модели в масштабе пор. Обычно проницаемость не является изотропной величиной, когда поры выровнены предпочтительно в одном направлении. Предположение об изотропной проницаемости для модели в масштабе пор сделано здесь, исходя из случайной ориентации пор, без какого-либо предпочтения в направлении. Для случая, когда проницаемость является анизотропной, дополнительные взаимозависимости для проницаемости модели в масштабе пор в поперечном направлении можно использовать для завершения модели. Коэффициент переноса масс Скорость переноса кислоты из жидкой фазы на границу раздела жидкость-твердое вещество внутри пор определяют количественно по коэффициенту переноса массы. Это играет важную роль в характеристике явлений растворения, поскольку коэффициент переноса масс определяет режим реакции для данной кислоты (уравнение (6. Коэффициент локального переноса масс зависит от локальной структуры пор, скорости реакции и локальной скорости флюида. Вклад каждого из этих факторов в значение коэффициента локального переноса масс исследован в деталях в документе авторов Gupta, N. и Balakotaiah,V.:"Heat and Mass Transfer Coefficients in Catalytic Monoliths", Chem. Engg. Sci., 56, 4771-4786 (2001) и в документе Balakotaiah, V. and West, D.H.: "Shape Normalization and Analysis of the Mass TransferControlled Regime in Catalytic Monoliths", Chem. Engg. Sci., 57, 1269-1286 (2002), причем оба эти документа приведены здесь в качестве ссылки. Для развития потока внутри прямой поры с произвольным поперечным сечением, хорошая аппроксимация к числу Шервуда, безразмерному значению коэффициента переноса массы, определяется по следующей формуле: где kс представляет коэффициент переноса массы,rр представляет радиус поры,Dm представляет коэффициент молекулярной диффузии,Sh представляет асимптотическое число Шервуда для поры,Rep представляет число Рейнольдса для поры,dh представляет гидравлический диаметр поры,х представляет расстояние от входа поры,Sc представляет число Шмидта (Sc=/Dm; гдепредставляет кинематическую вязкость жидкости). Предполагая, что длина поры обычно составляет несколько диаметров поры, средний коэффициент переноса массы может быть получен путем интегрирования вышеприведенного выражения по длине поры и задается следующим уравнением: где константы Sh и b (= 0,7/m0,5), m=отношение длины пор к диаметру, зависят от структуры пористой среды (отношение формы поперечного сечения поры и длины поры к гидравлическому диаметру). Уравнение (12) имеет ту же общую форму, что и корреляция Фросслинга, широко используемая для корреляции коэффициентов переноса массы в плотных слоях. Для плотного слоя из сфер Sh=2 и b=0,6. Это значение b близко к теоретическому значению 0,7, прогнозируемому с помощью уравнения (12) для m=1. Два члена с правой стороны уравнения (12) представляют собой вклад в число Шервуда из-за диффузии и конвекции кислоты соответственно. Хотя часть, связанная с диффузией, Sh, зависит от структуры поры, часть, связанная с конвекцией представляет собой функцию локальной скорости. Асимптотическое число Шервуда для пор с формой поперечного сечения в виде квадрата, треугольника и круга,равно 2,98, 2,50 и 3,66 соответственно. Поскольку значение асимптотического числа Шервуда представляет собой слабую функцию от структуры пор, для расчетов можно использовать типичное значение 3,0. Часть, связанная с конвекцией, зависит от числа Рейнольдса в поре и числа Шмидта. Для жидкостей типичное значение числа Шмидта составляет порядка одной тысячи, и предполагая значение 0,7 для b,приблизительная величина части, связанной с конвекцией числа Шервуда, из уравнения (12) составляет 7Rep1/2. Числа Рейнольдса для пор имеют очень малое значение из-за малого радиуса пор и низких скоростей инжекции кислоты, что делает вклад части, связанной с конвекцией, незначительным на исходных этапах растворения. По мере продолжения растворения, радиус пор и локальная скорость повышаются,что делает вклад, связанный с конвекцией, существенным. Внутри червоточины, где скорость намного выше, чем в другом месте среды, число Рейнольдса на уровне пор высоко, и величина части, связанной в конвекцией числа Шервуда, может превышать часть, связанную с диффузией. Влияние такого изменения на скорость переноса масс из-за конвекции, в зависимости от концентрации кислоты, может быть несущественным из-за чрезвычайно низкой площади раздела в областях с высокой пористостью. Кислота со-6 007285 временем может быть просто перенесена в результате конвекции вперед, без реакции, из-за малой площади раздела, когда вклад в результате конвекции на коэффициент переноса масс становится значительным. Хотя влияние части, связанной с конвекцией, коэффициента переноса масс на концентрацию кислоты внутри червоточины, предполагается незначительным, его важно учитывать в режиме равномерного растворения и для изучения переходов между различными режимами реакции, происходящими в среде из-за изменения скорости переноса масс. Наблюдаемое влияние кинетики реакции на коэффициент переноса масс оказалось слабым. Например, асимптотическое число Шервуда изменяется от 48/11 (=4,36) до 3,66 для случая от очень медленной реакции до очень быстрой реакции. Корреляция (12) учитывает влияние трех факторов, формы поперечного сечения пор, локальной гидродинамики и кинетики реакции на коэффициент переноса масс. Влияние извилистости поры на коэффициент переноса масс не включено в корреляцию. Интуитивно, извилистость поры способствует увеличению части, связанной с конвекцией, числа Шервуда. Однако, как указано выше, влияние части, связанной с конвекцией, коэффициента переноса масс на профиль концентрации кислоты, незначительно и не влияет на качественное поведение растворения. Коэффициент дисперсии флюида Для однородной, изотропной, пористой среды тензор дисперсии характеризуется двумя независимыми компонентами, а именно, продольным, De и поперечным, DeT, коэффициентами дисперсии. В отсутствие потока дисперсия растворенного вещества происходит только в результате молекулярной диффузии и De=DeT=0Dm, где Dm представляет коэффициент молекулярный диффузии, и 0 представляет собой константу, которая зависит от структуры пористой среды (например, извилистости). При наличии потока тензор дисперсии зависит от морфологии пористой среды, а также от потока на уровне пор и свойств жидкости. Обычно проблема взаимоувязывания тензора дисперсии с этими локальными переменными является достаточно сложной и аналогична определению тензора проницаемости в законе Дарси на основе структуры поры. В соответствии с предпочтительным вариантом выполнения настоящего изобретения, учитываются только простые аппроксимации тензора дисперсии. Относительное влияние конвекции на диффузный перенос на уровне пор характеризуется числом Пекле в поре, которое определяется по следующему уравнению: где u представляет собой величину скорости Дарси,dh представляет собой гидравлический диаметр поры. Для хорошо соединенной сети пор могут использоваться модели случайного блуждания и аналогия с плотно упакованными слоями, чтобы показать, что где х и т представляют собой числовые коэффициенты, которые зависят от структуры среды (х 0,5,т 0,1 для плотно упакованных слоев). Другие корреляции, используемые для Deх, имеют форму Уравнение (17), основанное на теории Тейлора-Ариса, обычно используют, когда степень связи между порами очень мала. Оно так же, как другие корреляции, описанные в литературе, прогнозирует,что как продольный, так и поперечный коэффициенты дисперсии, повышаются с ростом числа Пекле. В соответствии с предпочтительным вариантом выполнения настоящего изобретения, более простая взаимозависимость, задаваемая уравнениями (14) и (15), используется для завершения усредненной модели. В следующих секциях приведен анализ 1-D и 2-D версий двухшкальной модели (1-5). Одномерная модель Одномерная версия модели анализируется в этой секции для случая необратимой реакции с учетом предположения, что линейная кинетика (R(Cs)=ksCs). Для идентификации важных безразмерных групп,уравнения приведены в безразмерной форме для выбора длины керна L, в качестве шкалы характеристической длины в направлении потока, входной скорости u0, в качестве характеристической скорости и концентрации С 0 на входе, в качестве характеристической концентрации кислот. 1-D безразмерная модель для случая постоянной скорости инжекции определяется следующими уравнениями: где u, Cf, Cs и r представляют безразмерное значение скорости, безразмерное значение фазы и концентрации во флюиде и на границе раздела флюид-твердое вещество, а также безразмерное значение радиуса поры соответственно. Определение этих трех безразмерных групп в модели числа Дамкелера, Da, модуля Тиле, 2 и числа Nac расхода кислоты приведено ниже: где а 0 представляет собой исходное значение площади раздела на единицу объема,r0 представляет собой исходное усредненное значение радиуса поры модели в масштабе поры, представляет собой силу растворения кислоты. Число Da Дамкелера представляет собой отношение времени конвекции L/u0 ко времени реакции 1/ksa0 и модуль Тиле, 2 (или локальное число Дамкелера) представляет собой отношение времени диффузии (2r0)2/Dm на основе исходного усредненного значения диаметра (2r0) поры ко времени ks/(2r0) реакции. Хотя число Дамкелера представляет относительную важность реакции по сравнению с конвекцией в шкале Дарси, модуль Тиле представляет важность реакции в отношении к диффузии в масштабе пор. Число Nac расхода кислоты определяется как объем твердого вещества, растворенного в единице объема кислоты. Поле скорости в 1-D описывается уравнением (18), которое получено в результате комбинирования уравнения континуума с развитием пористости по уравнению (21) и однократного интегрирования по ,с использованием граничного условия u=1 на входе. Интеграл в уравнении представляет собой поправку по отношению к скорости из-за локального изменения объема во время растворения. Этот член является незначительным ввиду малых значений произведения DaNac. Для больших значений DaNac этим членом нельзя пренебрегать. Поскольку выполненные здесь расчеты представляют собой исследование качественного поведения растворения, членом, связанным с дисперсией, в уравнении баланса вещества пренебрегают. Пренебрежение членом дисперсии не изменяет качественную природу растворения. Уравнение (20) представляет собой безразмерную форму уравнения (6). Отношение (2r/Sh) равно отношениюks/kc, и параметры 2 и Sh зависят только от локальной реакции и скорости переноса массы. Это уравнение называют локальным уравнением. В следующей подсекции локальное уравнение (20) анализируют для идентификации различных режимов реакции и переходов между ними. Локальное уравнение Как указано выше, величина члена 2r/Sh или ks/kc в знаменателе локального уравнения определяет,представляет ли собой реакция режим кинетического управления или управления переносом масс. На практике реакцию рассматривают, как кинетический режим, если 2r/Sh0,l и как режим под управлением переноса масс если 2r/Sh10. Для значений 2r/Sh между 0,1 и 10, реакцию рассматривают как проходящую в промежуточном режиме. Модуль 2 Тиле в 2r/Sh определен в отношении исходных условий,но безразмерный радиус r пор и изменение Sh при изменении положения и времени делает член 2r/Sh функцией положения и времени. В любой заданный момент времени трудно определить, является ли реакция во всей среде управляемой переносом масс или управляемой кинетически, поскольку эти режимы реакции определены для локального масштаба и могут не быть соответствующими для всей системы. Ниже значения модуля Тиле для различных кислот сведены в виде таблицы для исходных значений радиуса пор в диапазоне 1-20 мкм. Предполагая типичное значение для числа Шервуда, равное 3, исходные значения 2r/Sh (r=1) и отношение концентрации Cs поверхности к концентрации Cf в жидкой фазе для различных кислот, представлены в таблице. Значения 2/Sh и Cs/Cf в таблице показывают, что все приведенные выше кислоты, за исключением НСl, находятся в кинетическом режиме во время исходных этапов растворения. Реакция между НСl и кальцитом проходит в промежуточном режиме. По мере продолжения реакции, размер пор увеличивается, что повышает значение 2r/Sh и приводит к переходу между различными режимами реакции. Например, реакция между НСl и кальцитом изменяется от промежуточного режима к режиму под полным управлением переноса масс, если безразмерный радиус пор увеличивается более чем в десять раз, и число Шервуда остается постоянным. Однако число Шервуда содержит как вклад диффузии, так и вклад конвекции, и когда радиус пор существенно увеличивается, число Шервуда также увеличивается из-за вклада конвекции. Это снижает величину 2r/Sh (или ks/kc). Таким образом, реакция может не достичь ограниченного режима переноса масс при увеличении радиуса поры. В этом случае большая часть реакции происходит в промежуточном режиме, и часть реакции происходит в режиме, управляемом переносом масс, поскольку площадь перехода, доступная для реакции, очень мала ко времени, когда реакция полностью достигает режима под управлением переноса масс. Аналогичные переходы между различными режимами реакции могут происходить для случая 0,25-М CDTA, который в исходном состоянии находится на границе кинетического и промежуточного режимов. Кроме того, неоднородность (переменный радиус пор) в среде может привести к различным режимам реакции в различных местах в среде. Вышеописанное иллюстрирует сложность при описании механизмов переноса и реакции во время растворения, из-за переходов и наличия неоднородностей. Тем не менее, эти переходы эффективно определяются с использованием двух переменных концентрации в локальном уравнении (20). Одиночная переменная концентрации не достаточна для описания обоих режимов под управлением кинетики и переноса масс одновременно. Цифровая имитация с помощью 1-D модели В этой секции представлено исследование параметров одномерной модели (18-21). Ниже сравнивают результаты моделирования с экспериментальными наблюдениями. Три безразмерных параметра модели представляют собой 2, Nac и Da. Цифровую имитацию выполняют при поддержании одного из параметров постоянным при изменении других двух параметров. Значение 0,2 использовали для исходного значения пористости во всех имитациях. Прорыв кислоты определяли как увеличение проницаемости керна в 100 раз от его исходного значения (К/К 0=100). Значение Nac фиксировали на уровне 0,0125 в первом наборе имитаций. Модуль Тиле изменяли от 2=0,001 до 2=100. График инжектируемого объема пор для прорыва в зависимости от числа Da Дамкелера представлен на фиг. 5 для 2=0,001. На этом графике представлено оптимальное число Дамкелера,при котором количество объемов пор кислоты, требуемой для прорыва керна, минимально. Для очень больших и очень малых значений числа Дамкелера количество кислоты, требуемое для прорыва, значительно больше. На фиг. 6 показано количество объемов пор, требуемое для прорыва для значений 2 0,001, 1,0 и 10,0. По мере увеличения значения 2, на графике показано увеличение оптимального числа Дамкелера и снижение минимального количества объемов пор, требуемого для прорыва. Во втором представленном здесь наборе имитаций исследуют влияние числа Nac емкости кислоты на поведение растворения. На фиг. 7 показан график инжектированного объема пор для прорыва в зависимости от числа Дамкелера, для значений числа расхода кислоты Nac=0,0125, Nac=0,0625 и Nac=0,125 для одинакового значения модуля Тиле 2=0,001. Минимальное количество кислоты, требуемое для прорыва,уменьшается при увеличении числа расхода кислоты. Такое уменьшение минимального количества объемов пор почти пропорционально увеличению Nac. На фиг. 8 показан график зависимости инжектируемого объема пор от Da, где как 2, так и Nac изменяются. На чертеже показан горизонтальный сдвиг кривых, когда модуль Тиле увеличивают, и вертикальный сдвиг для увеличения числа расхода кислоты.-9 007285 2 модель В этой секции представлены двумерные имитации, которые демонстрируют инициирование червоточины, распространение, плотность, протечку жидкости и конкуренцию между соседними червоточинами. Влияние неоднородности на структуру червоточины исследовали с использованием различных типов полей случайной проницаемости. Безразмерная двумерная модель и граничные условия для постоянной скорости инжекции, используемые в цифровых имитациях, представлены ниже В результате комбинирования уравнения континуума с законом Дарси, получают В уравнении (22) для поля давления членом /t накопления пренебрегают, предполагая квазиустойчивое состояние. Величина /t равна DaNacacs. Этим членом можно пренебречь, если произведениеDa на Nac будет мало. Уравнение (27) описывает граничное условие при постоянной скорости инжекции на входе, где (q/u0L) представляет собой безразмерную скорость инжекции, Н представляет собой ширину домена, и а 0 представляет собой соотношение размеров. Жидкость содержится в области с предотвращением ее утечки через боковые стенки, без использования граничных условий потока при у=0 и у=Н(уравнения (29) и (30. Неоднородность вводят как случайную флуктуацию f вокруг среднего значения 0. Амплитуду f изменяют от 10 до 50% вокруг среднего значения пористости. На первом этапе растворения поле давления в среде получают путем решения алгебраических уравнений, получаемых в результате дискретизации вышеприведенного уравнения, с использованием итеративного способа получения решения GMRES (обобщенный способ минимального остатка - GeneralizedMinimal Residual Method). Профили потока в среде вычисляют из профиля давления с использованием закона Дарси. Концентрацию кислоты в среде получают путем решения уравнение баланса вещества с использованием соответствующей схемы (Обратное преобразование Эйлера). Профиль пористости в среде затем обновляют с использованием новых значений концентрации. Этот процесс повторяют до прорыва кислоты. Структуры растворения и доминантное формирование червоточин На входе домена скорость инжекции кислоты поддерживают постоянной. По мере того как скорость инжекции изменяется, наблюдали различные типы структуры растворения аналогичные структурам, полученным в экспериментах. При имитации соотношение размеров и исходную пористость среды поддерживали на значениях 1 и 0,2, соответственно. Число Дамкелера уменьшалось при увеличении скорости инжекции. Для очень низких значений скорости инжекции (высокое значение Da) наблюдали поверхностное растворение. Кислота полностью потреблялась по мере того, как она поступала в среду. Для более высоких скоростей инжекции кислота образовывала каналы через среду, формируя червоточину. В этом случае кислота проходила через червоточину, не затрагивая остальную часть среды. При очень высоких скоростях инжекции кислота равномерно растворяет среду.- 10007285 Формирование доминантной червоточины от этапа инициирования является предпочтительным. Множество червоточин инициируется, когда кислота поступает в среду. Однако по мере дальнейшего растворения, большая часть кислоты поступает по каналам в несколько таких червоточин, увеличивая их размер. Предпочтительный поток кислоты в более крупные червоточины сдерживает рост более мелких каналов. В результате этого, один из этих трех каналов растет с большей скоростью, чем два других, отбирая всю кислоту и, таким образом, снижая скорость их роста. В вышеприведенных ситуациях червоточины инициировались из-за неоднородности среды, и конкурентный рост червоточин можно видеть на чертежах. Экспериментальное сравнение Влияние длины керна, концентрации кислоты, температуры, скорости диффузии и реакции на оптимальную скорость инжекции, исследовали в экспериментах. Влияние каждого из выше приведенных факторов на оптимальную скорость инжекции исследовали отдельно с использованием модели. Длина керна Наблюдали увеличение оптимальной скорости инжекции с увеличением длины керна. На фиг. 9 показаны экспериментальные данные объема пор, требуемых для прорыва, в зависимости от скорости инжекции, представленной в [4] для двух различных длин керна 5 см и 20 см. Кислота, используемая в этих экспериментах, представляла собой 7% НСl. Что касается безразмерных величин, число Nac расхода кислоты и модуль Тиле 2 были фиксированными, поскольку величины, от которых зависят эти параметры,концентрация кислоты, скорость реакции и диффузии являлись постоянными в этих экспериментах. Для фиксированных значений Nac и 2 теоретическое прогнозирование модели в отношении оптимальной скорости потока было аналогично представленному на фиг. 5 за исключением того, что модуль Тиле и оптимальное число Дамкелера были другими. Поскольку оптимальное число Дамкелера является фиксированным для фиксированных значений Nac и 2, оптимальные скорости инжекции в двух экспериментах могут быть взаимосвязаны с помощью следующего уравнения: При использовании уравнения (33), оптимальная скорость инжекции для длины керна 20 см может быть получена из оптимальной скорости инжекции для 5 см керна. Значение оптимальной скорости инжекции для 20 см керна составляло приблизительно u2=20)/5)(0,15)=0,6 см/мин, что близко к экспериментально наблюдавшейся скорости инжекции. Результаты в уравнении (33), когда оно расширено до масштабов пласта (L2/L1) предполагают,что максимальную длину червоточины получают, когда кислоту инжектируют с максимально возможной скоростью. Такой расчет инжекции кислоты с максимальной возможной скоростью инжекции при давлении ниже давления растрескивания был предложен авторами Williams, В.В., Gidley, J.L., and Schechter,R.S.: Acidizing Fundamentals, SPE Monograph Series, 1979, и наблюдался для увеличения эффективности имитации в некоторых полевых исследованиях, проведенных Paccaloni, G. and Tambini, M.: "Advances inAcid Fracturing: A Laboratory Evaluation of Acid/Rock Interactions", February 2001, SPE Prod.Facilities,22-29, которые получили аналогичные результаты в экспериментальных исследованиях с использованием кернов различной длины. Концентрация кислоты На фиг. 10 показано влияние различных значений концентрации кислоты 0,7, 3,5, 7 и 17,5% НСl в отношении пор для количества объемов пор для прорыва, которое наблюдали в экспериментах, выполненных автором Bazin. На чертеже показано уменьшение объема пор и увеличение оптимальной скорости инжекции, требуемое для прорыва, при увеличении концентрации кислоты. Изменение концентрации кислоты влияет только на число Nac расхода кислоты для реакции первого порядка. Для заданной кислоты или установленного значения модуля Тиле 2, на фиг. 8 показано, что увеличение числа расхода кислоты или эквивалентное увеличение концентрации кислоты уменьшает число объемов пор, требуемое для прорыва. Температура Наблюдения показали, что оптимальная скорость инжекции увеличивалась с ростом температуры. Постоянная скорости реакции увеличивается с повышением температуры, в результате чего увеличивается модуль Тиле 2. На фиг. 11 показано увеличение безразмерной скорости инжекции(2/Da=2r0u0/(Dma0L или различных значений модуля Тиле, которые соответствуют той же кислоте при различных температурах, полученное с использованием 1-D модели. Число расхода кислоты для всех вариантов моделирования составляло 0,0125. На чертеже показано увеличение безразмерного значения скорости инжекции с увеличением температуры или для низких - средних значений 2. Однако для очень- 11007285 больших значений модуля Тиле наблюдали очень слабую зависимость безразмерного значения скорости инжекции от модуля Тиле. При очень высокой температуре (или большом значении модуля Тиле) реакция полностью управляется переносом массы, и скорость поверхностной реакции или модуль Тиле играет незначительную роль в поведении растворения. Таким образом, оптимальная скорость инжекции слабо зависит от скорости поверхностной реакции в процессе, полностью управляемом переносом массы. Скорость диффузии кислоты Авторы Fredd и Fogler выполнили эксперименты с использованием кислот с различными значениями скорости диффузии, с одинаковым числом расхода кислоты. На фиг. 12 показаны кривые оптимальной скорости инжекции для этих кислот как функция скорости инжекции. Однако в этих экспериментах значения скорости реакции кислоты также были различны, таким образом, как постоянная ks скорости,так и коэффициент молекулярной диффузии Dm в модуле Тиле в этих экспериментах были различными. Значения модуля Тиле для различных кислот, использовавшихся в этих экспериментах, представлены в табл. 1. Так как в этих экспериментах число расхода кислоты Nac поддерживали постоянным, поведение растворения представляло собой только функцию модуля Тиле 2 и числа Da Дамкелера. На фиг. 12 показано, что кривые, соответствующие кислотам 0,25 М DTPA и 0,25 М EDTA (рН=13), очень близки друг к другу. Это поведение могло быть результатом почти равных значений модуля Тиле для этих двух кислот 2=0,0017 и 2=0,0024 для DTPA. Оптимальная скорость инжекции НСl значительно выше, поскольку у этой кислоты большое значение модуля Тиле 2=1. Качественная тенденция при повышении скорости инжекции при использовании модуля Тиле 2 для этой кислоты, прогнозируемая с помощью 1D модели, показана на фиг. 13. Объем прорыва Одномерная модель позволяет прогнозировать качественную зависимость оптимальной скорости инжекции и количества объемов пор, требуемого для прорыва, от различных факторов. Однако при этом оптимальное количество объемов пор, требуемое для прорыва, получается завышенным при прогнозировании по сравнению с экспериментальными результатами. Например, на основе модели прогнозируется,что для прорыва требуется приблизительно 200 объемов пор при использовании НСl в оптимальных условиях (фиг. 13), в то время как экспериментальное значение близко к представленному на фиг. 12. Подобное несоответствие между экспериментальным значением и прогнозом, полученным с использованием модели, (приблизительно 500 объемов пор) наблюдали для 2D сетевой модели, разработанной авторами Fredd и Fogler. Причина этого различия состоит в профиле скорости (уравнение (18, использованном в 1-D модели. При растворении кислота образует каналы в проводящей области, что приводит к увеличению локальной скорости. Для постоянной скорости инжекции, при использовании в экспериментах керна диаметром 3,8 см и червоточины диаметром 3,8 мм, скорость внутри червоточины может быть намного выше, чем входная скорость, что показано в следующих расчетах. Здесь uw представляет скорость внутри червоточины, Uinlet представляет скорость инжекции, Аcore иAwormhole представляют площади поперечного сечения керна и червоточины соответственно. Такое увеличение скорости в области из-за образования каналов не включено в профиль скорости 1-D по уравнению(18), где максимальная скорость в области не может быть выше, чем входная скорость. Поскольку в 2-D модели включено влияние образования каналов на профиль скорости, объем пор,требуемый для прорыва, определен существенно более низким, чем значение, прогнозируемое с помощью 1-D модели. Однако значение, полученное на основе 2-D модели, все еще выше, чем экспериментальный результат, поскольку максимальная скорость внутри области будет увеличиваться не как квадрат отношения диаметров (уравнение (34 червоточины и керна, а как отношение диаметров в двух измерениях. Считается, что полное 3-D моделирование позволит прогнозировать приблизительное значение объемов пор, требуемое для прорыва, на уровне, наблюдаемом в экспериментах. Уменьшение объемов пор для прорыва из-за образования каналов в 2-D модели показано на фиг. 14. Параметры 2=0,02 и Nac=0,07 поддерживали на постоянном уровне как в 1-D, так и в 2-D имитациях. Соотношение размеров (0) для 2-D имитации поддерживали равным 0,37. На чертеже показано уменьшение в пять раз оптимального количества объемов прорыва при переходе от 1-D к 2-D имитации, из-за образования каналов потока в червоточинах. Следует отметить, что оптимальное число Дамкелера для случая 2-D намного выше, чем для случая 1-D. Для одинаковых исходных условий в 1-D и 2-D увеличение числа Дамкелера (Da=ksa0L/u0) подразумевает уменьшение скорости инжекции. Таким образом, скорость инжекции, требуемая для оптимального прорыва, намного ниже в двух измерениях при сравнении с потоком в 1-D. Хотя скорость инжекции низка, в результате образования каналов получаются намного более высокие локальные скорости в соответствии с уравнением (34). Поскольку этот эффект отсутствует в 1-D модели, скорость жидкости, требуемая в ней для оптимального прорыва, намного выше. Вышеприведенные сравнения между результатами 1-D и 2-D моделей предполагают, что количества объемов пор, требуемых для прорыва для полной 3-D имитации в масштабе керна, должны быть меньше, чем полученные в результате 1-D и 2-D имитации и, вероятно, должны находиться в середине- 12007285 разрыва между экспериментальными значениями объема пор и значениями, полученными в результате цифровой имитации. Скорость инжекции для оптимальных условий также должна быть меньше, чем полученная в результате 1-D и 2-D моделирования. Чувствительность результатов к различным параметрам в модели и их влияние на структуру червоточины Зависимость времени прорыва для различных размеров сетки исследовали для случая Da=100,2=0,02, Nac=0,07 и соотношения размеров, равного единице. Различные размеры сетки, для которых выполняли имитацию, приведены нижеN1N2=5050, 8080, 80100, 10080, 100100. Здесь N1 представляет собой число точек сетки в направлении потока, и N2 представляет собой число точек сетки в поперечном направлении. Наблюдали, что безразмерное значение времени прорыва составило приблизительно 1,5 для всех случаев. Наблюдали слабое влияние экспонентыв корреляции проницаемость-пористость на время прорыва в режиме образования червоточин. Ниже приведены значения времени прорыва, полученные для различных значений . Влияние неоднородности Неоднородность вводили в модель как случайное поле пористости. Чувствительность результатов и зависимость структуры червоточины к исходной неоднородности исследовали с использованием двух типов полей случайной пористости. В первом случае исходную пористость в области вводили как случайную флуктуацию значений пористости вокруг среднего значения в каждой точке сетки в домене. Амплитуду флуктуации изменяли в диапазоне 10-50% от среднего значения. Результаты, полученные для флуктуации этой величины, наблюдали как качественно аналогичные. В значительно большем масштабе,чем промежутки сетки, этот тип поля пористости выглядит, как более или менее равномерный или однородный. Цифровая имитация в 2-D модели с использованием вышеуказанного поля неоднородной пористости показала, что модель позволяет определять инициирование червоточины, утечку жидкости, плотность червоточин и конкурентный рост червоточин. Однако наблюдали, что неоднородность, когда ее вводили в вышеуказанной форме, приводит к получению практически прямых червоточин с небольшими отклонениями их пути. Разветвление червоточин не наблюдали. Во втором случае неоднородность вводили в двух различных масштабах, а именно (а) случайная флуктуация пористости вокруг среднего значения в каждой точке сетки, (b) случайная флуктуация значений пористости вокруг другого, отличного от предыдущего, среднего значения над набором точек сетки (масштаб больший, чем масштаб сетки). Имитация с различными масштабами неоднородности показала, что ответвление, утечка флюида и изогнутые траектории червоточин, наблюдавшиеся в экспериментах, могут быть результатом различных типов неоднородности, присутствующей в карбонатах. Кислоту отклоняли в центр области, и в результате растворения получали прямую червоточину. Однако когда среднее значение пористости в центре домена увеличили до 0,4, наблюдали разветвление. В ходе исходных этапов растворения кислота протекает в канал и ее утечка происходит на кончике. В результате этого развиваются два ответвления, одно из которых растет гораздо быстрее другого и прорывается через керн. Если дополнительный регион низкой пористости вводят в середине области, присутствие региона с низкой пористостью внутри области можно интерпретировать как участок керна с очень низкой проницаемостью. В последнем случае кислота предпочтительно разветвляется вместо растворения породы в области с низкой проницаемостью. Поскольку такие области с низкой проницаемостью могут возникнуть в карбонатах, ответвления могут развиваться от червоточины, когда она входит в контакт с такими регионами. Приведенные выше имитации показывают, что сложная структура червоточины, наблюдавшаяся в экспериментах, и утечка флюида могут представлять собой результат различных масштабов неоднородностей, присутствующих в керне. Влияние таких видов неоднородности на время прорыва не исследовано систематически в литературе. Для изучения влияния неоднородности на формирование червоточин и чувствительность времени прорыва к неоднородности, в цифровую модель требуется вводить различные типы полей проницаемости как исходное условие. Один из способов ввода различных полей проницаемости состоит в увеличении случайной флуктуации проницаемости вокруг среднего значения поля. Однако, как указано выше, эта процедура всегда приводит к получению поля проницаемости, которое является более или менее однородным в гораздо более крупном масштабе, чем шкала сетки. Другой подход для генерирования различных полей проницаемости состоит в вводе длиныкорреляции в поле проницаемости. При изменении длины корреляции могут быть сгенерированы различные- 13007285 масштабы неоднородности. При этом близкие друг к другу местоположения в области, имеют коррелированные значения проницаемости, и для мест положений, разделенных расстоянием, значительно большим, чем , значения проницаемости не скоррелированы. Максимальная амплитуда флуктуации значения проницаемости вокруг среднего значения в каждой точке сетки управляется переменной 2 распределения проницаемости. При изменении длиныкорреляции переменной 2 и распределения могут быть получены исходные значения неоднородности для шкал с различной длиной. Когда коррелированная длина становится очень маленькой, получают случайное поле проницаемости первого типа. При этом генерируемые поля проницаемости с использованием первого подхода, представляют собой частный случай случайных полей проницаемости, генерируемых с использованием второго способа. Например, на фиг. 15(а)-15(с) показаны случайно коррелированные поля проницаемости, сгенерированные на одномерном домене единичной длины. Значениякорреляции длины, для фиг. 15(а)-15(с) составляют 0,1, 0,05 и 0,01 соответственно. По мере того, как длина корреляции уменьшается, поле проницаемости становится более похожим на генерируемое с использованием первого подхода. Здесь для генерирования полей проницаемости модели 1-D использовали экспоненциальную ковариационную функцию с переменной 2, равной двум. Вышеуказанная процедура обеспечивает преимущество, состоящее в возможности систематического исследования влияния неоднородности на формирование червоточин и структуры. Разработана новая усредненная модель, предназначенная для описания потока и реакции в пористой среде. Представленная здесь модель описывает процесс обработки кислотой, как взаимодействие между процессами в двух различных масштабах, в масштабе Дарси и в масштабе пор. Модель можно использовать с моделями различных масштабов пор, которые представляют структуры различных типов пород, без влияния на уравнение масштаба Дарси. Эта новая модель является неоднородной по природе,и ее можно использовать как для режимов, управляемых переносом массы, так и для режимов, управляемых кинетически реакцией. Цифровые имитации новой модели для случая 1-D показывают, что модель позволяет определять качественные свойства обработки кислотой. Двумерная имитация модели демонстрирует способность модели определять инициирование червоточин, распространение, утечку жидкости и конкурентный рост червоточин. Влияние неоднородности на формирование червоточин также можно исследовать с использованием полей с различной исходной пористостью. Количественный показатель,представляющий практический интерес, - количество объемов пор, требуемое для прорыва, определяют,как имеющий строгую зависимость от образования каналов потока. Моделирование, представленное здесь, является предварительным и влияние неоднородности на формирование червоточин и структуру червоточин, например, разветвление червоточин, утечку жидкости, связанную с разветвлением и т.д., не полностью изучено. Поскольку модель в соответствии с настоящим изобретением позволяет выполнять точное масштабирование, обработка, проводимая в ходе имитации, может быть рассчитана по результатам исследования первого полученного керна из месторождения путем определения набора параметров, представляющих указанный керн из месторождения, причем указанный набор параметров включает параметры масштаба Дарси и параметры масштаба пор, и выполнения моделирования в соответствии с настоящим изобретением. Указанный набор параметров предпочтительно включает число Шервуда, тензор дисперсии,модуль Тиля и число Пекле. Кроме того, также собирают данные, представляющие неоднородности,присутствующие в керне месторождения. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ моделирования процесса повышения проницаемости пористой среды, включающего осуществление химической реакции в пористой среде, в котором формируют модель процесса взаимодействия пористой среды и реагента, при этом модель представляют системой уравнений химических реакций и уравнений переноса масс, используемых для построения моделей в масштабе Дарси и моделей в масштабе пор, при этом концентрация Cf реагента в текучей фазе пор и концентрация Cs указанного реагента на границе раздела флюид-твердое вещество пор принимаются отличными от нуля. 2. Способ по п.1, в котором Cs и Cf рассчитывают путем определения скорости переноса реагентов из текучей фазы на границу раздела флюид-твердое вещество внутри пор с помощью коэффициента переноса масс с учетом как диффузионного вклада, так и вклада в результате конвекции. 3. Способ по п.1 или 2, в котором указанная пористая среда представляет собой подземную формацию. 4. Способ по п.3, в котором указанная обработка для интенсификации добычи представляет собой обработку кислотой. 5. Способ по п.4, в котором указанную обработку для интенсификации добычи выбирают из группы, состоящей из обработки матрицы кислотой и образования трещин в результате обработки кислотой. 6. Способ по любому из пп.1-5, в котором указанная химическая реакция включает растворение пористой среды. 7. Способ по п.6, в котором модель включает описание реакционного растворения пористой среды с использованием объединенных глобальных и локальных уравнений.- 14007285 8. Способ по п.7, в котором указанное уравнение включает проницаемость, тензор дисперсии и средний радиус пор, а также коэффициент локального переноса масс. 9. Способ по п.1, в котором поток химического реагента моделируют с использованием ненулевого расходящегося поля U скорости. 10. Способ по п.2, дополнительно включающий использование коррелированных случайных полей для учета различных масштабов неоднородности. 11. Способ по п.2, в котором вклад за счет диффузии в коэффициент переноса масс представлен с помощью асимптотического числа Шервуда для поры. 12. Способ по п.11, в котором безразмерное значение коэффициента переноса масс (число Шервуда(12),где Sh представляет асимптотическое число Шервуда для поры, b представляет константу, зависящую от отношения длины поры к диаметру поры, Rep представляет число Рейнольдса для поры и Sc представляет число Шмидта. 13. Способ по п.12, в котором b=0,7/m0,5, где m представляет отношение длины к диаметру поры. 14. Способ моделирования процесса повышения проницаемости пористой среды, включающего осуществление химической реакции в пористой среде, в котором формируют модель процесса взаимодействия пористой среды и реагента, при этом модель представляют системой уравнений химических реакций и уравнений переноса масс, используемых для построения моделей в масштабе Дарси и моделей в масштабе пор, при этом концентрация Cf реагента в текучей фазе пор и концентрация Cs указанного реагента на границе раздела флюид-твердое вещество пор принимаются отличными от нуля, а также осуществляют дискретизацию скорости переноса реагентов из текучей фазы на границу раздела флюидтвердое вещество пор с использованием коэффициента переноса масс, с учетом как вклада за счет диффузии, так и вклада за счет конвекции. 15. Способ повышения проницаемости подземной формации, включающий осуществление химической реакции в подземной формации, включающий получение керна из месторождения, определение набора параметров, представляющих указанный керн из месторождения, причем указанный набор параметров включает параметры в масштабе Дарси и параметры в масштабе пор, и выполнение способа в соответствии с любым из предыдущих пунктов с использованием указанного набора параметров. 16. Способ по п.15, в котором указанный набор параметров включает число Шервуда, тензор дисперсии, модуль Тиле и число Пекле. 17. Способ по п.15 или 16, в котором указанный набор параметров дополнительно включает данные, относящиеся к неоднородностям.