Способ определения минимального количества испытаний преимущественно строительных материалов и изделий
Номер патента: 14390
Опубликовано: 29.10.2010
Авторы: Осипов Сергей Николаевич, Пилипенко Владимир Митрофанович
Формула / Реферат
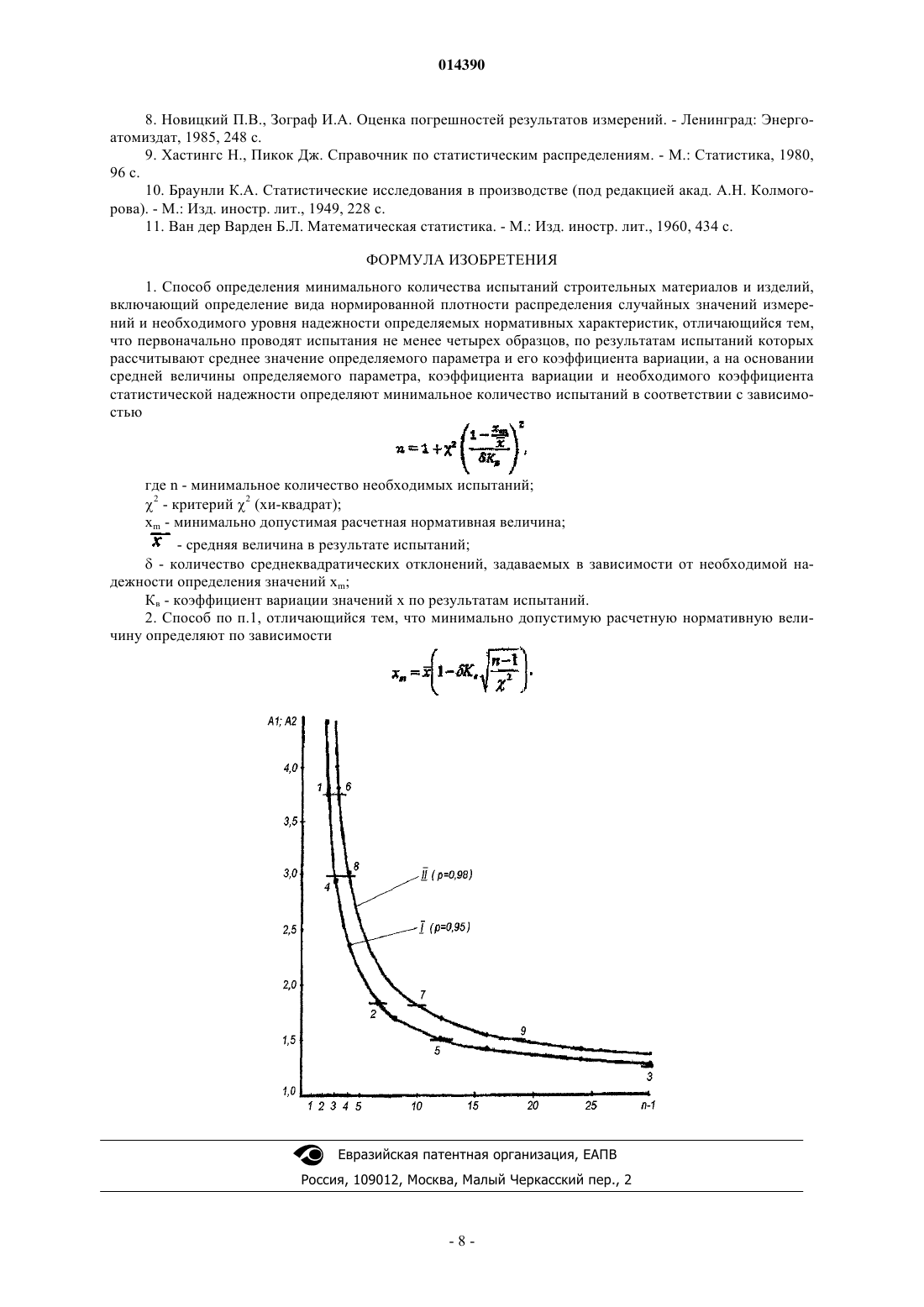
1. Способ определения минимального количества испытаний строительных материалов и изделий, включающий определение вида нормированной плотности распределения случайных значений измерений и необходимого уровня надежности определяемых нормативных характеристик, отличающийся тем, что первоначально проводят испытания не менее четырех образцов, по результатам испытаний которых рассчитывают среднее значение определяемого параметра и его коэффициента вариации, а на основании средней величины определяемого параметра, коэффициента вариации и необходимого коэффициента статистической надежности определяют минимальное количество испытаний в соответствии с зависимостью
![]()
где n - минимальное количество необходимых испытаний;
c2- критерий c2(хи-квадрат);
xm - минимально допустимая расчетная нормативная величина;
![]() - средняя величина в результате испытаний;
- средняя величина в результате испытаний;
d - количество среднеквадратических отклонений, задаваемых в зависимости от необходимой надежности определения значений xm;
Кв- коэффициент вариации значений х по результатам испытаний.
2. Способ по п.1, отличающийся тем, что минимально допустимую расчетную нормативную величину определяют по зависимости
![]()
Текст
СПОСОБ ОПРЕДЕЛЕНИЯ МИНИМАЛЬНОГО КОЛИЧЕСТВА ИСПЫТАНИЙ ПРЕИМУЩЕСТВЕННО СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ И ИЗДЕЛИЙ Изобретение относится к области оценки надежности, качества и других показателей преимущественно строительных материалов, изделий, процессов и систем, а также производственной и окружающей среды с целью экологической и производственной безопасности и планирования технологических процессов и направлено на повышение надежности нормативных характеристик материалов и изделий, создание удобного для практического применения способа двухступенчатого учета статистической изменчивости прочности испытываемых в лабораторных условиях материалов и изделий. Суть способа в том, что первоначально проводят испытания не менее четырех образцов, по результатам испытаний определяют средние значения определяемого параметра и его коэффициента вариации, а на основании средней величины определяемого параметра, его возможного уменьшения или увеличения, коэффициента вариации и необходимого коэффициента статистической надежности определяют минимальное количество испытаний. Осипов Сергей Николаевич, Пилипенко Владимир Митрофанович (BY)(71)(73) Заявитель и патентовладелец: НАУЧНО-ИССЛЕДОВАТЕЛЬСКОЕ И ПРОЕКТНО-ТЕХНОЛОГИЧЕСКОЕ РЕСПУБЛИКАНСКОЕ УНИТАРНОЕ ПРЕДПРИЯТИЕ "ИНСТИТУТ НИПТИС ИМ. АТАЕВА С.С." (BY) 014390 Изобретение относится к области оценки надежности, качества и других показателей преимущественно строительных материалов, изделий, процессов и систем, а также производственной и окружающей среды с целью экологической и производственной безопасности и планирования технологических процессов. Происходящие в последние годы обрушения крупных по площади наружных перекрытий различных спортивных (спортзал школы в Краснопольске в РБ, 2004 г., Трансвааль-парк в Москве, 2004 г., бассейн в Москве, 2005 г. и др.), торговых (Басманный рынок в Москве, 2006 г.), зрелищных(г. Катовице, ПНР, 2005 г. и др.) и других залов в разных странах (Франция, ФРГ и др.) с большими человеческими жертвами свидетельствуют об определенных недостатках в нормативно-технической документации многих стран, так как при разработке таких документов должны быть учтены не только чисто технические, но и другие факторы, существенно зависящие от случайных явлений. Даже принятый в странах Европейского Союза уровень надежности для отдельных показателей строительных материалов и изделий в 95% в соответствии с СТБ ИСО 5725-1-2002 части 1-6 можно считать недостаточным, что подтверждается результатами обследования покрытий над спортзалами 16 школ, аналогичных Краснопольской [1]. В несущих фермах всех обследованных школ выявлены эксплуатационные дефекты, которые при дальнейшем развитии могли бы привести к катастрофическим последствиям, подобных Краснопольской школе. Все спортзалы построены в конце 80-х гг. прошлого столетия. Таким образом, из 17 покрытий спортзалов обрушилось одно, что составляет на 2004 г. вероятность 5,9%, а надежность работоспособности соответственно 94,1%. Поэтому при строительстве технически сложных и критически нагруженных сооружений необходимо особенно тщательно учитывать все возможные случайные факторы, определяющие устойчивость таких сооружений к внешним и внутренним воздействиям. Необходимо отметить, что общая надежность сложных, особенно строительных, сооружений обычно должна соответствовать 0,9999. В этом случае при нормальном распределении случайных событий разрушения для уровня обеспеченности 0,9999 необходимо принимать процентную точку t=3,72. Расчетное сопротивление материала R получают делением нормативного сопротивления Rn на соответствующий коэффициент надежности m [2]. Величина m устанавливается статистической обработкой необходимого числа данных испытаний, причем обеспеченность значений должна составлять не ниже 0,95, т.е. прочность материала не менее чем в 95% случаев испытаний должна быть равной или большей Rn. При этом коэффициент надежности по материалу m вводится для учета возможных отклонений его прочности в неблагоприятную сторону. Величина m устанавливается нормами в зависимости от свойств материала и статистической изменчивости последних. Например, стандартами и техническими условиями для различных марок стали рекомендуются значения m=1,025-1,15 [2]. Для одноступенчатого контроля во многих нормативно-технических документах уровень обеспеченности (надежность определения параметра) принят в размере 0,95. Однако в ГОСТе 23615-79 в п.4.3 сказано: "При нормальном распределении геометрического параметра стабильность статистических характеристик в мгновенных выборках и выборках малого объема n30 единицам проверяют по попаданию их значений в доверительные интервалы, границы которых вычисляют для доверительной вероятности не менее 0,95", что устанавливает уровень надежности 0,95 и выше. Сопоставляя приведенные выше результаты обследования [1] и случай обрушения кровли в спортзале Краснопольской школы с необходимым уровнем безопасности зданий и сооружений для здоровья и жизни человека, четко видим явную недостаточность уровня надежности 0,95 для подобных объектов. Необходимо отметить, что еще в ГОСТе 23616-79 при вводе изменения 1 справочного приложения 4 для планов выборочного контроля строительных материалов и изделий предусматривалось увеличение объема выборки при нормальном законе распределения контролируемого параметра и погрешности измерений =2,5n, где- возможная предельная погрешность измерения и n - средняя квадратическая погрешность измерений. Здесь коэффициент 2,5 обеспечивает надежность результатов измерений около 0,994, что почти на порядок выше 0,95. Рекомендуемое увеличение объема выборки особенно существенно (на 13-23%) при низком приемочном уровне дефектности (0,25%). Следует отметить, что анализируя нормативные документы разных лет (ГОСТ 18242-72, СТ СЭВ 548-77, СТ СЭВ 1673-79, СТБ ГОСТ Р 50779.71-2001, ИСО 2859.1-89, СТБ ИСО 5725-1-2002), можно найти много различий не только в методологии, но и результатах расчетов. В соответствии с новейшим СТБ 1544-2005 показатели прочности бетона на сжатие и растяжение определяются по ГОСТу 10180, или ГОСТу 17624, или ГОСТу 22690, или ГОСТу 22783, или СТБ 1151,или ГОСТу 28570. Такое разнообразие рекомендуемых нормативных документов указывает на существенную неопределенность принципов выбора уровней надежности определения прочностных свойств бетонов. Однако в п.3.37 СТБ 1544-2005 при определении класса бетона по прочности на сжатие рекомендуется учет статистической изменчивости прочности с обеспеченностью 0,95 (с уровнем надежности 0,95). По ГОСТу 18105-86 требуемая прочность бетона на сжатие принимается в зависимости от среднего коэффициента вариации Кв прочности по всем партиям за анализируемый период. Если перевести приве-1 014390 денные в табл. 2 ГОСТа 18105-86 значения коэффициента требуемой прочности (статистической) в зависимости от Кв, в диапазоне Кв 0,06-0,20 изменяются в пределах 1,06-1,57, что соответствует t=1,06-1,9 для разных видов бетона. Такие значения t=1,06-1,9 при нормальном законе распределения соответствуют уровню обеспеченности (надежности) N(Кв)=0,855-0,97. Как показывают последние исследования по контролю прочности бетона [3], определение требуемой прочности с учетом статистической изменчивости, в зависимости от значений нормируемой прочности и коэффициентов вариации прочности является недостаточно обоснованным. При этом в начальном периоде производства (от недели до 2 месяцев) число единичных значений прочности должно составлять не менее 30. В качестве аналога можно принять предложение М.И. Бруссера и др. [4] о новой системе стандартизации и о правилах контроля прочности бетонов, где в общем случае расчета требуемой прочности(Rm) статистический коэффициент прочности (Кс) определяется в зависимости от фактического коэффициента вариации прочности (Кв) и числа испытаний (n) по формуле, рекомендованной в [4]:- средняя прочность бетона на сжатие, МПа; гдеt1 - процентная точка нормального распределения, зависящая от обеспеченности гарантированной прочности (t1=2 для тяжелого бетона, что соответствует уровню обеспеченности 0,977);t2=0,84-20%-ная точка нормального распределения, определяемая риском потребителя [3]. Согласно исследованиям [5], выполненным на бетонах, приготовленных в лабораторных условиях,стандартное отклонение увеличивается пропорционально средней прочности бетона, но угол наклона этой зависимости менее 45, что свидетельствует об уменьшении величины Кв с ростом средней прочности. Как показывает компьютерная корреляционная обработка, произведенная заявителями для приведенных в [5] 80-ти экспериментальных определений, аппроксимирующая зависимость для среднего относительного коэффициента вариации имеет вид где =0,0415; b=0,0732; с=0,1246 МПа-1 при коэффициенте корреляции r=-0,39, что связано с большим разбросом значений заметно уменьшается. На пример, при увеличении с 10 до 50 МПа уменьшается с 0,06 до 0,04, что опровергает правильность постоянства нормативного заложенного в ГОСТе 18105-86 при обеспеченности 0,95. Зависимости среднего стандартного отклонения от средней прочности в условиях строительства [6] показывают, что при увеличении 0,09 и примерно в 2,5-4 раза больше лабораторных результатов, а значения Необходимо отметить значительный разброс величин коэффициентов вариации вокруг аппроксимирующей кривой для лабораторных определений прочности бетона [5]. Относительный коэффициент вариации разброса 80-ти значений составляет Кв.о=0,355, что свидетельствует о существенной неустойчивости этой зависимости. Следует указать, что разброс значений Кв.о вокруг зависимости имеет примерно аддитивный характер и не совсем соответствует нормальному закону распределения, который из-за отсутствия необходимых данных обычно принимается почти во всех нормативных документах. По крайней мепри изменении следует ожидать в условиях применения бетона ре, такой же разброс значений при строительстве зданий и сооружений. При этом практический предельный уровень Кв примерно в 1,5 раза больше средних величин В результате анализа многочисленных литературных и нормативных источников в качестве прототипа выбран последний СТБ 1544-2005 [7]. В этом нормативно-техническом документе [7] в качестве базового уровня прочности принята гарантированная прочность бетона на базе испытания кубов с размером ребра 150 мм, с учетом статистической изменчивости прочности с обеспеченностью 0,95. Для бетонов классов С 8/10-С 50/60 требуемая прочность бетона на сжатие, контролируемая по кубам, определяется при коэффициенте вариации 13,5% (0,135) по зависимости, предусматривающей по-2 014390 вторное увеличение требуемой прочности по сравнению с гарантируемой прочностью в 1,285 раза. Расчетная формула для определения расчетной строительной прочности бетона на сжатие по средней величине лабораторных (хсж.л) испытаний кубов бетона при распределении значений в соответствии с нормальным законом распределения может быть записана в виде Если принять Кв.л=0,135, то что примерно соответствует 3 стандартным отклонениям от величины Приведенные выше зависимости уточняют и усложняют общую картину, но не изменяют общего подхода к определению величины коэффициента статистической надежности результатов испытаний лабораторных образцов бетона на прочность, в котором выражены следующие недостатки прототипа: низкий уровень обеспеченности (0,95) расчетного значения прочности бетона, что явно недостаточно особенно при тиражировании в строительстве схемных решений; возможные существенные отклонения реальных законов распределений плотностей вероятности значений прочности от нормального закона, которые не укладываются в перечень распределений, обеспечивающих уровень обеспеченности 0,95 при t=1,6 или 1,64 [8]; отсутствие учета погрешности определения величины Кв, зависящей от количества (n) производственных определений значений хсж [9]. Перечисленные недостатки в значительной мере обоснованы применением одноступенчатого учета статистической изменчивости прочности испытываемых в лабораторных условиях образцов бетона. В силу указанных причин, приведенная в [7] методика статистической оценки надежности расчетных величин прочности бетона может оказаться неудовлетворительной, что будет справедливо и для других строительных материалов и изделий. Поэтому, учитывая возможные отклонения плотности вероятности реализации параметра от нормального закона, общий уровень учета статистической изменчивости следует принимать для различных узлов, деталей и процессов в зависимости от важности влияния используемого параметра на целостность и безопасность изделия не менее 0,98. Целью предлагаемого изобретения является повышение надежности нормативных характеристик преимущественно строительных материалов и изделий, создание удобного для практического применения способа двухступенчатого учета статистической изменчивости прочности испытываемых в лабораторных условиях материалов и изделий, предполагающего достижение уровня обеспеченности, соответствующего значению коэффициента статистической надежности результатов испытаний лабораторных образцов материалов и изделий на прочность не менее 0,98 расчетного значения их прочности. Поставленная задача решается достижением технического результата посредством предлагаемого способа повышения надежности значений нормативных характеристик строительных материалов и изделий, включающего определение вида нормированной плотности распределения случайных значений измерений и необходимого уровня надежности определяемых нормативных характеристик. Согласно способу по изобретению первоначально проводят испытания не менее четырех образцов изделий, по результатам испытаний определяют средние значения определяемого параметра и его коэффициента вариации,а на основании средней величины определяемого параметра, его возможного уменьшения или увеличения, коэффициента вариации и необходимого коэффициента статистической надежности определяют минимальное количество испытаний в соответствии с номограммой (чертеж) или аналогичной для соответствующего значения где n - минимальное количество необходимых испытаний; 2 - критерий 2 (хи-квадрат);m - минимально допустимая расчетная нормативная величина;- средняя величина в результате испытании;- количество среднеквадратических отклонений в зависимости от вероятности реализации значений х; Кв - коэффициент вариации значений х по результатам испытаний. При ограниченном количестве необходимых испытаний согласно заявляемому способу расчетную нормативную величину определяют по зависимости В 1969 г. было проведено сравнение интегральных кривых равномерного, трапецеидального, треугольного и нормального распределения и путем их усреднения получена некоторая средняя зависимость. Эта зависимость была включена в виде рекомендуемого приложения 2 в ГОСТ 8.009-72 для опре-3 014390 деления t в пределах Рв=0,7-0,99 без установления вида распределения, что соответствовало t=1,64 для Рв=0,9, t=1,9 для Рв=0,95 и t=2,1 при Р=0,99. Ранее (1966-1968 гг.) для класса экспоненциальных распределений, к которым в определенной мере можно отнести также нормальное распределение и распределение Лапласа, было установлено [8], что для Рв=0,9 необходимо t1,65, а для Рв=0,95 необходимо t2,0. Подобные исследования позволили прийти к выводу [8], что для многих видов распределений с погрешностью 0,05 ( - среднеквадратичное отклонение) в случае принятия t=1,6 можно рассчитывать на одностороннюю доверительную вероятность (надежность) Рв 0,95. Эта величина t=1,6 при надежности Рв=0,95 вошла во многие методики расчета и нормативные документы. Как указывается в [8, с. 42], очень часто доверительные границы рассчитывают, вводя ничем не обоснованное предположение о том, что вид закона распределения будто бы точно известен. В частности, вычисляют по небольшой выборке в 20-30 измерений среднеквадратичное отклонение , а затем принимают погрешность с доверительной вероятностью Рв=0,997 при t=3 на основании предположения о нормальности закона распределения. Однако по ограниченным экспериментальным данным получаются не точные доверительные значения, а лишь их оценки. Достоверность квантильных оценок резко повышается с понижением значений Рв, а при постоянстве Рв - с ростом числа измерений n. Поэтому квантильные оценки с большими доверительными вероятностями можно определить только при большом числе измерений. При обработке вариационного ряда в соответствии с рекомендацией [8] n[2(l+n отб)]/(l-Pe), гдеn отб - количество измерений, отброшенных с концов вариационного ряда, и при n отб=1 для различных значений Рв количество необходимых измерений в отсутствии надежных сведений о законе плотности распределения значений параметра приведено в табл. 1. Таблица 1 Для выбора значения t при оценке статистической надежности определяемого параметра, например прочности бетона на сжатие, заявители данного изобретения сравнили возможную надежность определения расчетной величины параметра, если плотность его вероятных значений соответствует нормальному или одностороннему экспоненциальному закону. Последний выбран вследствие его явной асимметричности и особым свойствам В других весьма важных для рассматриваемой проблемы распределениях хи-квадрат и Стьюдента для оценки статистической надежности определяемого параметра необходимо использовать не только значения критериев 2 и Стьюдента tc, но и количество степеней свободы nc, которые в данном случае составляют nc=n-1. В этих распределениях используется два параметра, что несколько усложняет их практическое использование. Как указывает К.А. Браунли [10, с. 48], вероятный доверительный предел истинного значения дисперсий при определенном уровне значимости для любых объемов выборок, в том числе малых, можно вычислить по формуле где d - дисперсия значений определяемого параметра, полученных при испытаниях, d=m2;m - вероятная максимальная величина среднеквадратического отклонения значений, полученных при испытаниях определяемого параметра;k2 - дисперсия, подсчитанная по данным выборки результатов испытаний с n - 1 степенями свободы;n - количество полученных значений параметра; 2 - значение критерия 2 (хи-квадрат), верхний доверительный предел которого в зависимости от поставленной задачи принимается в пределах уровня зависимости, аналогичного вероятности реализации Рв=0,90-0,99, что соответствует 1-10% вероятности появления, более высоким, чем расчетные значенияm. Аналогичная расчетная формула встречается также в других работах по математической статистике(например, Б.Л. Ван дер Варден [11, с. 169]). Выбор количественной оценки уровня значимости имеет большое практическое значение. Так, при-4 014390 Рв=0,95 в 5% случаев возможно превышение расчетной величины m, а при Рв=0,99 - только в 1% случаев. При этом значение 2 уменьшается с 0,103 до 0,020 [10, табл. II], т.е. почти в 5 раз, что эквивалентно увеличению m в 2,24 раза и существенному уменьшению расчетной величины определяемого параметра. Как указывает редактор монографии акад. А.Н. Колмогоров [10, с. 217-218], в каждом отдельном случае наше доверие к гипотезе после какой-либо ее проверки никогда нельзя отделить от ее оценки apriori до данной проверки, что учитывается в классической теории оценки вероятностей гипотез на основе теоремы Байеса. Часто целесообразно введение нескольких уровней значимости (вероятностей р). Если какая-либо гипотеза ставится под сомнение при переходе критерием границ, соответствующих уровню значимости Рв=0,95 (верхний доверительный предел) или 0,05 (нижний доверительный предел), и в этом случае производятся дополнительные испытания для проверки, безоговорочно же отбрасываются лишь при переходе границ, соответствующих уровню значимости Рн=0,01 [10, с.218]. Учитывая дополнительный к общепринятому учет вероятного увеличенияза счет действия стохастических факторов, в нашем случае можно принять Рв=0,95. Для значительных выборок (n30) К.А. Браунли [10, с.48] предлагает использовать тот факт, что стандартное отклонение стандартного отклонениясоставляет k/2n, и выражение (6) можно заменить на где tc - критерий Стьюдента (псевдоним английского статистика B.C. Госсета [11, с. 148]). Вместо среднеквадратических отклонений удобно использовать коэффициенты вариации вследствие безразмерности и наглядности уровня возможного разброса значений выборочных средних величин. Тогда в соответствии с (6) где Кв.т- вероятная максимальная величина коэффициента вариации. Тогда минимальную величину испытываемого параметра m можно определить по формулам:- среднее значение параметра; где- количество стандартных отклонений в зависимости от вероятности реализации значений параметра. При необходимости оценки количества определений (реализаций) параметра в случае нормального закона распределения часто используют общеизвестную формулу где рн - допустимая погрешность определения искомой величины. Однако с учетом возможных стохастических колебаний коэффициента вариации можно получить Как видно из этой формулы, количество необходимых испытаний при учете возможного вероятностного разброса значений Кв, по крайней мере, при небольшом количестве испытаний (n10) существенно больше по сравнению с отсутствием учета стохастических колебаний коэффициента вариации. Для других видов распределения из (9) можно получить путем простейшей итерации определяется необходимое количеОткуда по заданной величине ство испытаний n. Изложенные результаты исследований позволяют предложить новый способ повышения надежности значений нормативных характеристик изделий, включающий определение вида нормированной плотности распределения случайных значений измерений, использующий характеристики изделия, и их необходимого уровня надежности, основанный на том, что расчетную величину характеристики принимают с учетом допустимого уровня погрешности коэффициента вариации события, что учитывается через коэффициент Кс Учет статистической погрешности определения коэффициента вариации позволяет по-новому подойти к определению необходимого количества определений параметра в зависимости от значения коэффициента вариации и принятой величины нормированного отклонения доверительной границы от среднего значения параметра, что зависит от необходимого уровня надежности. Учитывая влияние уровня колебания единичных значений определяемого параметра на величину коэффициента статистической характеристики параметра изделия, предлагается новая методика определения Кс, заключающаяся в предварительном проведении 4-5 измерений, по результатам которых рассчитывают коэффициент вариации Кв. После этого по заданным значениям t1, p и tc определяют величину Кс, а при необходимости уменьшения Кс проводят дополнительную серию измерений характеристики этого параметра того же материала, изделия или процесса и для суммарного значения n определяют Кс. Для определения необходимого количества испытаний образцов на чертеже приводится расчетная номограмма, взятая из зависимости (8) На чертеже показана кривая I для значений надежности оценки коэффициента вариации р=0,95 и кривая II для р=0,98. Предлагаемый способ предусматривает двухступенчатость учета статистической изменчивости прочности испытываемых в лабораторных условиях материалов и изделий, которая заключается в том,что для предварительной оценки вариационности определяемой величины необходимо первоначальное испытание малой серии образцов, а затем последующее определение минимального количества испытаний по расчетной номограмме (чертеж), а также с использованием зависимости (4) и с учетом (13)-(15). Учитывая увеличение величины Кс с ростом n, далее решают экономическую задачу по определению оптимального значения n, исходя из сравнения стоимости проведения измерений и экономической выгоды от повышения расчетного уровня параметра. В качестве примера приводится расчет количества необходимых измерений прочности образцов бетона и расчетной (нормативной) прочности бетона на сжатие. 1-й этап испытаний. В результате определения прочности бетонных кубов с размерами граней 150 мм получены следующие данные: 1=35,2, 2=45,8, 3=42,3 и 4=37,9 МПа. Среднее значение Для приведенных данных величина коэффициента вариации Кв=11,6%, параметр 2=0,711. При n=4 и допустимой надежности 95% расчетная величина коэффициента вариации составит что почти в 3 раза больше измеренного. Для получения существенно меньшей величины Кв.т нужно произвести хотя бы 20 определений прочности бетонных образцов. Тогда Кв.т=0,136. Если не учитывать влияние погрешности коэффициента вариации, то для нормального закона распределения при р=5%n46, т.е. в 2,3 раза больше. Величина коэффициента Кс, учитывающего статистический запас надежности при n=4, составит Кс=1-2,0-0,34=0,32. Если воспользоваться методикой расчета, приведенной в СТБ 1544-2005, то коэффициент, учитывающий статистическую надежность, составит Кс=(1-1,640,116)(1-1,640,135)=0,63, что в 2 раза больше. Таким образом, по предлагаемой методике для данных условий коэффициент статистического запаса прочности составляет 1/0,323,1, а по СТБ 1544-2005 1/0,63=1,6, что почти в 2 раза меньше. 2-й этап испытаний. В результате проведения дополнительных 16 измерений бетонных кубов величина общего расчет-6 014390 ного коэффициента вариации составила Кв=0,136. Величина коэффициента статистической надежности По СТБ 1544-2005: Кс=(1-1,640,11)(1-1,640,135)=0,64. В результате значительного увеличения количества лабораторных измерений n (с 4 до 20) значения Кс, определяемые по предлагаемой методике и СТБ 1544-2005, сблизились. Из данного примера видно существенное влияние увеличения количества измерений искомого параметра. В случае n=30, как это рекомендовано в [7], Кс=0,66, что также примерно соответствует 0,64. В качестве примера определения необходимого количества испытаний образцов на чертеже приведены точки пересечений (обозначены от 1 до 9) кривых I и II с условными горизонтальными прямыми соответствующими зависимости при конкретных значениях всех параметров. и различных значениях других паВ табл. 3 приведены результаты определений n при раметров, соответствующим точкам 1-9 на чертеже. Как видно из данных этой таблицы только при =1,6 и Кв=0,05 достаточно проведение 3-х испытаний. При реальных значениях Кв 0,1 и необходимости обеспечения более высокой надежности (р=0,98) следует проводить испытания 12 и более образцов. Таблица 3 Предлагаемый способ повышения надежности значений нормативных характеристик учитывает возможность существенного отклонения плотности распределения значений параметра от нормального особенно при малом количестве измерений. Количество измерений может быть ограничено количеством образцов для испытаний по причине высокой стоимости оригинальности или сложности изготовления. При ограниченном по техническим,временным или экономическим причинам количестве необходимых испытаний расчетную нормативную величину определяют по зависимости Предлагаемый способ применим для оценки возможных максимальных воздействий силовых нагрузок, например снежных, ветровых и др., а также максимальных значений различных недостаточно детерминированных параметров во многих природных и технических процессах. К отрицательным факторам предлагаемого изобретения можно отнести зависимость от определяемого нижнего или верхнего пределов снижения или увеличения расчетных (нормативных) величин определяемого параметра. Основные технические задачи изобретения решаются посредством предложенного способа, так как его применение легко реализуемо на практике и предполагает безусловное повышение надежности и безопасности эксплуатации изделий, материалов и производственных процессов, достигаемое за счет того, что при таком способе учитывается уровень надежности коэффициента вариаций. Источники информации. 1. Лапчинский А.К. Эксплуатационная надежность железобетонных безраскосых ферм. - Мн.: Архитектура и строительство,1, 2005, с.114-116. 2. Винокуров Е.Ф., Балыкин М.К., Голубев К.А., Заяц В.Н., Макарук П.Н. Справочник по сопротивлению материалов. - Мн.: Наука и техника, 1988, 464 с. 3. Блещик Н.П., Тур В.В., Кравченко В.В. К вопросу о контроле прочности бетона в свете требований ГОСТ 18105-86 и общеевропейского стандарта EN 206-1: 2001. - Мн.: Строительная наука и техника, 1, 2005. 4. Бруссер М.И., Дорф В.А., Малиновский А.Г., Хаютин Ю.Г. Новая система стандартов по правилам контроля прочности бетонов. - М.: Бетон и железобетон,2, 1984, с. 32, 33. 5. Nieville A.M. Wlasciwosci betonu. - Arkadz, Warszywa 1977 oraz Polski Cement. Krakow, 2000. 6. Korzewka S., Mames J. Wztrzymalosc gwarantowana betonow predukowanych w zaklach-7 014390 8. Новицкий П.В., Зограф И.А. Оценка погрешностей результатов измерений. - Ленинград: Энергоатомиздат, 1985, 248 с. 9. Хастингс Н., Пикок Дж. Справочник по статистическим распределениям. - М.: Статистика, 1980,96 с. 10. Браунли К.А. Статистические исследования в производстве (под редакцией акад. А.Н. Колмогорова). - М.: Изд. иностр. лит., 1949, 228 с. 11. Ван дер Варден Б.Л. Математическая статистика. - М.: Изд. иностр. лит., 1960, 434 с. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ определения минимального количества испытаний строительных материалов и изделий,включающий определение вида нормированной плотности распределения случайных значений измерений и необходимого уровня надежности определяемых нормативных характеристик, отличающийся тем,что первоначально проводят испытания не менее четырех образцов, по результатам испытаний которых рассчитывают среднее значение определяемого параметра и его коэффициента вариации, а на основании средней величины определяемого параметра, коэффициента вариации и необходимого коэффициента статистической надежности определяют минимальное количество испытаний в соответствии с зависимостью где n - минимальное количество необходимых испытаний; 2 - критерий 2 (хи-квадрат);xm - минимально допустимая расчетная нормативная величина;- средняя величина в результате испытаний;- количество среднеквадратических отклонений, задаваемых в зависимости от необходимой надежности определения значений xm; Кв - коэффициент вариации значений х по результатам испытаний. 2. Способ по п.1, отличающийся тем, что минимально допустимую расчетную нормативную величину определяют по зависимости
МПК / Метки
МПК: E04G 23/00, G01N 3/32
Метки: способ, испытаний, строительных, материалов, количества, преимущественно, определения, изделий, минимального
Код ссылки
<a href="https://eas.patents.su/9-14390-sposob-opredeleniya-minimalnogo-kolichestva-ispytanijj-preimushhestvenno-stroitelnyh-materialov-i-izdelijj.html" rel="bookmark" title="База патентов Евразийского Союза">Способ определения минимального количества испытаний преимущественно строительных материалов и изделий</a>
Предыдущий патент: Гибридные эластификаторы и способы их изготовления
Следующий патент: Фармацевтическая композиция для лечения ожогов и способ ее получения
Случайный патент: Установка для выравнивания подачи твердого порошкообразного материала в горелку для концентрата печи суспензионной плавки или переработки суспензии