Способ и устройство хранения программы для цифровой производной давления
Формула / Реферат
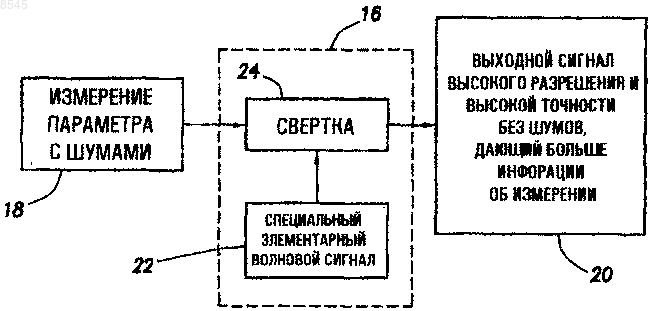
1. Способ генерирования выходного сигнала, не содержащего шумов, в ответ на входной сигнал с шумами, являющийся сигналом измерения, заключающийся в том, что осуществляют свертку входного сигнала, содержащего шумы, с элементарным волновым сигналом, генерируют выходной сигнал в ответ на этап свертки, не содержащий шумов.
2. Способ по п.1, отличающийся тем, что входной сигнал является функцией, представляющей сигнал измерения давления в скважине, который содержит шумы.
3. Способ по п.1, отличающийся тем, что выходной сигнал является производной входного сигнала, причем выходной сигнал не содержит шумов.
4. Способ по п.3, отличающийся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом осуществляют свертку входного сигнала с элементарным волновым сигналом с использованием уравнения
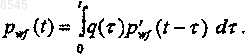
5. Способ по п.4, отличающийся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала.
6. Способ по п.5, отличающийся тем, что производную элементарного волнового сигнала формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой.
7. Способ по п.3, отличающийся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом осуществляют свертку входного сигнала с элементарным волновым сигналом с использованием уравнения
8. Способ по п.7, отличающийся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала.
9. Способ по п.8, отличающийся тем, что производную элементарного волнового сигнала формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой.
10. Способ по п.1, отличающийся тем, что дополнительно осуществляют свертку выходного сигнала с элементарным волновым сигналом, генерируют дополнительный выходной сигнал в ответ на этап дополнительной свертки, при этом дополнительный выходной сигнал не содержит шумов.
11. Способ по п.10, отличающийся тем, что выходной сигнал является первой производной входного сигнала, причем выходной сигнал не содержит шумов.
12. Способ по п.11, отличающийся тем, что дополнительный выходной сигнал является второй производной входного сигнала, причем дополнительный выходной сигнал не содержит шумов.
13. Способ по п.12, отличающийся тем, что на этапе осуществления свертки входного сигнала с элементарным волновым сигналом и на этапе дополнительной свертки выходного сигнала с элементарным волновым сигналом используют уравнение
14. Способ по п.13, отличающийся тем, что элементарный волновой сигнал формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой.
15. Способ по п.12, отличающийся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом и этапе дополнительной свертки выходного сигнала с элементарным волновым сигналом используют уравнение
16. Способ по п.15, отличающийся тем, что элементарный волновой сигнал формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой.
17. Способ по п.1, отличающийся тем, что входной сигнал является частной функцией, содержащей набор из выборок цифровых данных, представляющих сигналы измерения давления в скважине, которые включают в себя шумы.
18. Способ по п.17, отличающийся тем, что выходной сигнал является производной частной функции, причем производная частной функции не содержит шумов.
19. Способ по п.18, отличающийся тем, что на этапе свертки цифрового входного сигнала с элементарным волновым сигналом осуществляют свертку входного сигнала с элементарным волновым сигналом с использованием уравнения
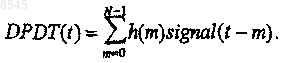
20. Способ по п.19, отличающийся тем, что элементарный волновой сигнал является производнойэлементарного волнового сигнала.
21. Способ по п.20, отличающийся тем, что производную элементарного волнового сигнала формируют из ограниченного по полосе частот преобразованного сигнала идеального дифференцирующего устройства, при этом преобразованный сигнал с ограниченной полосой частот имеет расчетное значение частоты отсечки ограниченной полосы частот.
22. Способ по п.21, отличающийся тем, что расчетное значение частоты отсечки ограниченной полосы частот выбирают в качестве значения, выше которого шумы являются основной составляющей полного сигнала.
23. Способ по п.20, отличающийся тем, что вычисляют один или несколько коэффициентов элементарного волнового сигнала с использованием способа Чебышева, используя алгоритм замен Ремеза.
24. Устройство хранения программы, считываемой машиной, содержащей программу из команд, выполняемых машиной, для осуществления этапов способа генерирования выходного сигнала, не содержащего шумов, в ответ на входной сигнал, являющийся сигналом измерения, который содержит шумы, в указанном способе осуществляют свертку входного сигнала, содержащего шумы, с элементарным волновым сигналом, генерируют выходной сигнал в ответ на этап свертки, не содержащий шумов.
25. Устройство по п.24, отличающееся тем, что упомянутый входной сигнал является функцией, представляющей сигнал измерения давления в скважине, который содержит шумы.
26. Устройство по п.24, отличающееся тем, что выходной сигнал является производной входного сигнала, причем выходной сигнал не содержит шумов.
27. Устройство по п.26, отличающееся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом используется уравнение
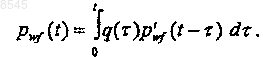
28. Устройство по п.27, отличающееся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала.
29. Устройство по п.28, отличающееся тем, что производную элементарного волнового сигнала формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой.
30. Устройство по п.26, отличающееся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом используется уравнение
31. Устройство по п.30, отличающееся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала.
32. Устройство по п.31, отличающееся тем, что производную элементарного волнового сигнала формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой.
33. Устройство по п.24, отличающееся тем, что дополнительно осуществляют свертку выходного сигнала с элементарным волновым сигналом, генерируют дополнительный выходной сигнал в ответ на этап дополнительной свертки, причем дополнительный выходной сигнал не содержит шумов.
34. Устройство по п.33, отличающееся тем, что выходной сигнал является первой производной входного сигнала, причем выходной сигнал не содержит шумов.
35. Устройство по п.34, отличающееся тем, что дополнительный выходной сигнал является второй производной входного сигнала, при этом дополнительный выходной сигнал не содержит шумов.
36. Устройство по п.35, отличающееся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом и на этапе дополнительной свертки выходного сигнрыр с элементарным волновым сигналом используют уравнение
37. Устройство по п.36, отличающееся тем, что элементарный волновой сигнал формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой.
38. Устройство по п.35, отличающееся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом и на этапе дополнительной свертки выходного сигнала с элементарным волновым сигналом используют уравнение
39. Устройство по п.38, отличающееся тем, что элементарный волновой сигнал формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой.
40. Устройство по п.24, отличающееся тем, что упомянутый входной сигнал является частной функцией, содержащей набор из выборок цифровых данных, представляющих сигналы измерения давления в скважине, которое включает в себя шумы.
41. Устройство по п.40, отличающееся тем, что выходной сигнал является производной частной функции, причем производная частной функции не содержит шумов.
42. Устройство по п.41, отличающееся тем, что на этапе свертки цифрового входного сигнала с элементарным волновым сигналом осуществляется свертка входного сигнала с элементарным волновым сигналом с использованием уравнения
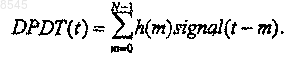
43. Устройство по п.42, отличающееся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала.
44. Устройство по п.43, отличающееся тем, что производная элементарного сигнала формируется из ограниченного по полосе частот преобразованного сигнала идеального дифференцирующего устройства, при этом преобразованный сигнал с ограниченной полосой частот имеет расчетное значение частоты отсечки ограниченной полосы частот.
45. Устройство по п.44, отличающееся тем, что расчетное значение частоты отсечки ограниченной полосы частот выбрано в качестве значения, выше которого шумы являются основной составляющей полного сигнала.
46. Устройство по п.43, отличающееся тем, что один или несколько коэффициентов элементарного волнового сигнала вычисляется с использованием способа Чебышева, используя алгоритм замен Ремеза.
47. Способ генерирования выходного сигнала, не содержащего шумов, в ответ на входной сигнал с шумами, являющийся сигналом измерения, заключающийся в том, что осуществляют свертку входного сигнала, содержащего шумы, с элементарным волновым сигналом, генерируют выходной сигнал в ответ на этап свертки, при этом выходной сигнал представляет производную входного сигнала и не содержит шумов.
48. Устройство хранения программы, считываемой машиной, содержащей программу из команд, выполняемых машиной, для осуществления этапов способа генерирования выходного сигнала, не содержащего шумов, в ответ на входной сигнал с шумами, являющийся сигналом измерения, заключающийся в том, что осуществляют свертку входного сигнала, включающего в себя шумы, с элементарным волновым сигналом, генерируют выходной сигнал в ответ на этап свертки, причем выходной сигнал представляет производную входного сигнала и не содержит шумов.
Текст
008545 Область техники, к которой относится изобретение Настоящее изобретение относится к программному обеспечению цифровой производной давления,которое хранится в компьютерной системе и предназначено для приема результата или функции измерения, содержащей "шум", например результата измерения давления в нефтяной или газовой скважине, для осуществления свертки функции измерения с элементарным волновым (импульсным) сигналом и для формирования выходного сигнала, имеющего высокую разрешающую способность и высокую точность,в котором практически отсутствуют "шумы" и который позволяет пользователю интерпретировать выходной сигнал высокого разрешения и высокой точности, чтобы получить большее количество информации об измерении. Если функция измерения представляет собой измерение давления в нефтяном или газовом резервуаре, функцию измерения давления, содержащую "шумы", свертывают с производной элементарного волнового сигнала, тем самым, формируя производную функции измерения давления,имеющую намного более высокую разрешающую способность или разрешение, которая практически не имеет "шумов". Отсутствие "шумов" в производной функции измерения давления с более высоким разрешением, которое сформировано сверткой, позволяет интерпретировать производную функции измерения давления и получать большее количество информации об измерении давления и резервуаре. Предшествующий уровень техники Использование данных испытания (рабочих параметров) скважины для определения характеристик резервуара в последнем десятилетии привело к значительному прогрессу. Существенный прогресс при использовании математических способов позволяет обеспечить аналитическое решение сложных задач о потоках резервуара, которые ранее решались только посредством численных способов. Значительный вклад в данную область техники внесли работы Ozkan и Raghavan1-3, в которых преобразование Лапласа и методы истоков и стоков были систематизированы, чтобы вычислять распределения давления для различных сложных скважин и резервуаров. Использование преобразования Лапласа позволяет учитывать природные трещины (разломы)4, изменяемую норму добычи 5 (хранилища скважины) и смешанный продукт 6 эффективным образом. При объединении с алгоритмом Stehfest7 численного инвертирования решений в пространстве Лапласа во временную область получают прямой подход с точки зрения программной реализации к разработке эффективных и расширяемых библиотек аналитических решений для уравнения диффузии. Для ситуаций, в которых аналитические процедуры являются ограниченными (например, сложная геометрия, многофазный поток) можно использовать недавно разработанное программное обеспечение, специально предназначенное, чтобы в интерактивном режиме моделировать динамические данные испытания скважины для переходного режима, используя способы конечных разностей (например, испытание скважин GeoQuest WellTest 200). Достижения, полученные при измерении динамических данных неустановившегося давления для переходного режима, или неустановившегося давления, дополнили эти новые способы решения, т.к. обеспечили устойчивость и разрешающую способность, необходимые, чтобы воспринимать сложности скважинной/резервуарной системы, которые, возможно, в противном случае были бы незамеченными. В настоящее время возможно измерять давление с разрешающей способностью 0,001 фунт на кв.дюйм(PSI) с 10-секундным взятием выборок, или дискретизацией, и с устойчивостью (уходом параметров) менее чем три фунта на кв.дюйм/год.8. Интерпретация и измерение данных испытания скважины, за некоторыми недавними исключениями, были усовершенствованы по отдельности. Примечательное исключение составляют два исследования, представленные в работах Veneruso, et al.9,10. В первой работе показано, как ошибки в измерении давления влияют на анализ результатов испытаний скважины, использующий подход анализа передаточной функции. Влияния измерительных средств, например уход параметров и разрешающей способности,включены в аналитическое моделирование испытаний скважины, чтобы оптимизировать технические характеристики осуществления испытаний с эффективными по затратам приборами. Во второй работе обсуждаются ключевые способы сбора данных и передачи данных в дополнение к предоставлению хорошего краткого обзора электронных процессов, относящихся к выполнению измерений давления, скорости потока (или расхода) и температуры. В данном описании раскрыто дальнейшее сокращение разделения между достижениями в интерпретации результатов испытаний скважины и достижениями в технологии измерений с учетом указанных выше достижений. Конкретно, используются строгие математические модели цифровой обработки сигналов, чтобы объединить характеристики процесса измерений в ходе испытаний скважины с имеющимся знанием физики резервуара и усовершенствовать способ определения производной давления для диагностирования и интерпретации динамических данных неустановившегося давления. Термин "производная" означает дифференцирование по времени, представленное на абсциссе соответствующего графика в логарифмическом масштабе; в общем случае, это следует рассматривать в виде функции суперпозиции по времени. Наиболее существенным достижением в интерпретации результатов испытания скважины в прошлом десятилетии стало использование производной давления, как описано в работах Bourdet et al.,11-14 в качестве базового инструмента для диагностирования поведения скважины и резервуара. Оно обеспечивает основу для современной методологии 15 интерпретации результатов испытания скважины и является-1 008545 общепринятой и необходимой функциональной возможностью для множества программных обеспечений, предназначенных для интерпретации результатов испытания скважины, используемых в настоящее время. Во многих ситуациях, однако, производная измеренных данных не является интерпретируемой или, хуже, является неверно интерпретируемой аналитиком вследствие различных артефактов процесса измерения и дифференцирования, в совокупности называемых "шумами". В статье 16 утверждается, что"главным недостатком производной давления является то, что необходимо создавать данные производных посредством численного дифференцирования измеренных данных давления. Результирующие данные производной давления часто имеют шумы и трудны для интерпретации. Несмотря на то, что использовались различные способы "сглаживания", чтобы уменьшать шумы, было некоторое опасение, что процедуры сглаживания могут изменять основные свойства данных". Это мнение признает большинство инженеров, связанных с интерпретацией данных испытания скважины. Были использованы различные алгоритмы, при попытке устранить или уменьшить неизбежные шумы, связанные с численным дифференцированием измеренных данных. Например, в работе Bourdet etal.14 рассматривается полиномиальное приближение данных, или приближение многочленом, и взятие аналитической производной многочлена. Эта процедура, кроме того, что является громоздкой, изменяет форму исходных данных. Вторая приведенная процедура состоит в вычислении третьей производной данных и последующем интегрировании дважды. Этот способ имеет тенденцию давать ложные колебания при поздних временах (близких к концу) и в течение бесконечного радиального потока. В настоящее время принятой практикой является использование способов прошлых столетий, разработанных Ньютоном и Стирлингом, для интерполирования таблиц данных (левосторонней, правосторонней или центральной разности, обычно с использованием трех точек, или трехточечной разности). С точки зрения частотной области это, по всей вероятности, фильтры верхних частот и полосовые фильтры, которые чрезмерно усиливают шумы высоких частот и искажают "истинную" кривую dp/dt. Данные затем обычно сглаживают посредством выбора точек, используемых в вычислении, на достаточном расстоянии от рассматриваемой точки. Это расстояние, заданное как L в ссылке 14, выражают в терминах соответствующей временной функции. Идею сглаживания производной некоторые подвергают сомнению вследствие субъективного выбора L. Если L выбрано слишком большим, то динамические особенности фактического сигнала будут искажены. Тем не менее, судя по общепринятому использованию этого способа, в программном обеспечении для испытания скважины, он стал наиболее популярным. В работе Akima17 предлагается немного отличающийся подход, в соответствии с которым используют наклон рассматриваемой точки и двух точек с каждой стороны. Многочлен третьей степени, представляющий часть кривой между парой заданных точек, определяют в соответствии с координатами и углами наклона в двух точках. Затем вычисляют производную многочлена. Независимо от используемого способа численного дифференцирования и независимо от приемов,используемых для уменьшения разброса в результирующих данных производной, для анализа часто оставляют данные, не являющиеся полностью репрезентативными для скважинной/резервуарной системы,которую следует идентифицировать. В данном описании представлен новый способ дифференцирования данных давления при испытании скважины, названный способом цифровой (дискретной) производной давления (СЦПД). СЦПД формирует наиболее точную и репрезентативную кривую dp/dt путем использования физики резервуара и физики измерительных средств. Способ является эффективным и может быть использован либо для данных в реальном масштабе времени, либо для записанных данных. Не требуется осуществлять модификацию измерительных технических средств. Кроме того, могут быть предусмотрены границы погрешностей и механизмы управления качеством, указывающие окончание переходного процесса (т.е. испытание отношения сигнал-шум), что позволяет оптимально использовать объем памяти записывающего устройства (регистратора). Могут использоваться дополнительные способы цифровой обработки (ЦОС, DSP) сигналов, например, избыточная дискретизация, чтобы дополнительно повысить качество СЦПД. СЦПД формируется посредством свертки выборок измеренного давления со специальным элементарным волновым сигналом. Этот элементарный волновой сигнал формируется на основании характеристики одиночной выборки (отклика на одиночную выборку) ограниченного по полосе частот, оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой(КИХ, FIR). СЦПД основан на строгой математической основе цифровой обработки (ЦОС, DSP) сигналов, физике резервуара и характеристиках системы измерения давления. Краткое описание сущности изобретения Технической задачей настоящего изобретения является устранение вышеупомянутых ограничений,связанных с интерпретацией полученного на основании измерения сигнала, включающего в себя шумы,посредством свертки этого сигнала с элементарным волновым сигналом, и формирования выходного сигнала, не содержащего шумов. Поставленная задача согласно первому аспекту настоящего изобретения решена путем создания способа, который реагирует на входной сигнал измерения с шумами, для генерирования выходного сигнала измерения без шумов, способ заключается в осуществлении свертки входного сигнала с элементарным волновым сигналом, и генерирования выходного сигнала в ответ на свертку, при этом формируемый-2 008545 выходной сигнал не содержит шумов. Другим аспектом изобретения является создание устройства хранения программы, считываемой машиной, предназначенного для реализации способа генерирования выходного сигнала, представляющего измерение, который не содержит шумов, в ответ на входной сигнал, представляющий измерение, которое содержит шумы, причем способ включают в себя осуществление свертки входного сигнала с элементарным волновым сигналом, и генерирование выходного сигнала в ответ на свертку, причем выходной сигнал не содержит шумов. Следующим аспектом настоящего изобретения является создание способа, в котором осуществляют обработку входного сигнала с шумами, для генерирования выходного сигнала, представляющего измерение, не содержащего шумов, способ содержит свертку входного сигнала, включающего шумы, с элементарным волновым сигналом, и генерирование выходного сигнала в ответ на свертку, выходной сигнал представляет производную входного сигнала, выходной сигнал не содержит шумов. Еще одним аспектом настоящего изобретения является создание считываемого машиной устройства хранения программы, содержащей команды, выполняемые машиной, чтобы выполнить этапы способа,в котором из измеренного входного сигнала с шумами генерируют выходной сигнал, не содержащий шумов, способ содержит следующие этапы: осуществление свертки входного сигнала, включающего в себя шумы, с элементарным волновым сигналом; генерирование выходного сигнала в ответ на свертку,выходной сигнал представляет производную входного сигнала и не содержит шумов. Подробное описание и конкретные примеры представляют предпочтительный вариант осуществления настоящего изобретения и даются только в качестве иллюстрации, поскольку различные изменения и модификации в пределах существа и объема изобретения станут очевидными специалисту в данной области техники из рассмотрения нижеследующего подробного описания. Краткое описание чертежей В дальнейшем настоящее изобретение поясняется подробным описанием предпочтительного варианта осуществления со ссылкой на сопроводительные чертежи, на которых фиг. 1 изображает блок-схему вычислительной системы, которая содержит "программное обеспечение цифровой производной давления" для выполнения "способа цифровой производной давления"(СЦПД) согласно изобретению; фиг. 2 и 3 - блок-схему блока свертки функции измерения, включающей в себя шумы, с элементарным волновым сигналом, для генерирования выходного сигнала, имеющего высокое разрешение и высокую точность, не содержащего шумов, и формирования большего количества информации об измерении,при этом выходной сигнал высокого разрешения и высокой точности представляет производную первого порядка функции измерения, если измеряемым параметром является давление в нефтяном или газовом резервуаре согласно изобретению; фиг. 4 - блок-схему блока сверток по фиг. 2 и 3 для генерирования производной второго порядка для конкретной измеряемой функции, значительное количество информации определяют на основании производной второго порядка частной функции благодаря отсутствию шумов согласно изобретению; фиг. 5 - схему функции передачи давления измерительным средством согласно изобретению; фиг. 6 - диаграммы наложения спектров согласно изобретению; фиг. 7 - диаграмму частотной характеристики идеального дифференцирующего устройства; фиг. 8 - диаграмму сравнения производной Ньютона и идеальной производной; фиг. 9 - диаграмму выборки для известных дифференцирующих устройств; фиг. 10 - диаграмму сравнения производной Стирлинга и идеальной производной; фиг. 11 - диаграмму коэффициентного элементарного волнового сигнала на основании алгоритма замен (переменных) Ремеза; фиг. 12 - диаграмму частотной характеристики коэффициентного элементарного волнового сигнала(сигнала для определения коэффициентов); фиг. 13 - диаграмму спектральной плотности мощности, вычисленной для типичных моделей резервуара согласно изобретению; фиг. 14 - диаграмму входного сигнала и конечно-разностной производной согласно изобретению; фиг. 15 - диаграмму сравнения спектров сигнала и сигнала + шумы согласно изобретению; Фиг. 16 - диаграмму сравнения конечно-разностной производной и СЦПД, согласно изобретению; фиг. 17 - диаграмму данных давления с логарифмической выборкой согласно изобретению; фиг. 18 - диаграмму равномерно и логарифмически разнесенных коэффициентов Ремеза согласно изобретению; фиг. 19 - диаграмму наклона (крутизны) давления для обычных режимов потока согласно изобретению; фиг. 20 - диаграмму кривых для 20log(delta) в зависимости от частоты для N=4, 8, 16, 32 и 64 согласно изобретению; фиг. 21 - диаграмму кривых для 20log(delta) в зависимости от частоты для N=5, 9, 17, 33 и 65 согласно изобретению; фиг. 22 - диаграммы элементарных волновых сигналов для трех различных длин фильтра согласно-3 008545 изобретению; фиг. 23 - диаграммы частотной характеристики для трех коэффициентных элементарных волновых сигналов согласно изобретению; фиг. 24 - диаграммы характеристик СЦПД для трех различных длин фильтра согласно изобретению; фиг. 25 - диаграмму определения fc для отношения единичного сигнала к шуму согласно изобретению; фиг. 26 - диаграмму СЦПД для fc=0,10 согласно изобретению; фиг. 27 - диаграмму СЦПД для fc=0,05 согласно изобретению; фиг. 28 - диаграмму СЦПД для fc=0,025 согласно изобретению; фиг. 29 - диаграмму СЦПД с аналитической и конечно-разностной производной согласно изобретению; фиг. 30 - диаграммы в двойном логарифмическом масштабе для дельта-приращения давления и производной для примера 1 согласно изобретению; фиг. 31 - диаграмму в логарифмическом масштабе для дельта-давления и производной для примера 1 согласно изобретению; фиг. 32 - диаграмму спектральной плотности мощности для примера 1 согласно изобретению; фиг. 33 - диаграмму СЦПД для примера 1 согласно изобретению; фиг. 34 - диаграмму в двойном логарифмическом масштабе дельта-давления и производной для примера 2 согласно изобретению; фиг. 35 - диаграмму в логарифмическом масштабе дельта-давления и производной для примера 2 согласно изобретению; фиг. 36 - диаграмму спектральной плотности мощности для примера 2 согласно изобретению; фиг. 37 - диаграмму СЦПД для примера 2 согласно изобретению; фиг. 38 - диаграмму сравнения СЦПД с обычной производной, L=0,09 согласно изобретению; фиг. 39 - диаграмму сравнения различных сглаживающих значений L согласно изобретению; фиг. 40 - схему окна ввода параметров СЦПД согласно изобретению. Описание предпочтительного варианта осуществления На фиг. 1 представлена вычислительная система 5 или рабочая станция, или персональный компьютер. Вычислительная система 5 содержит процессор 10, соединенный с системной шиной, запоминающее устройство 12, соединенное с системной шиной, и записывающее устройство или устройство 14 вывода на экран, соединенное с системной шиной. Запоминающее устройство 12 является устройством хранения программы или машиночитаемым носителем, который хранит программу, озаглавленную "Программное обеспечение цифровой производной давления" 16. Программное обеспечение 16 цифровой производной давления загружено в запоминающее устройство 12 вычислительной системы из отдельного устройства хранения программ, например из постоянного запоминающего устройства на компакт-диске (ПЗУ-КД,CD-ROM), где записано программное обеспечение 16. Вычислительная система 5 принимает входные данные, представляющие измерение 18 с шумами. Измерения 18 содержат "шумы" и не интерпретируются. Когда процессор 10 выполняет программу 16 получения цифровой производной давления, то записывающее устройство или устройство 14 вывода на экран будет отображать выходной сигнал 20 высокого разрешения и высокой точности без шумов. Поскольку "шумы" отсутствуют, выходной сигнал 20 без шумов может быть интерпретирован заказчиком. Вычислительная система 5 может быть персональным компьютером (ПК, PC), рабочей станцией или универсальной ЭВМ. Примеры возможных рабочих станций включают в себя рабочую станцию Silicon Graphics Indigo 2, или рабочую станцию Sun SPARC, или рабочую станцию Sun ULTRA, или рабочую станцию Sun BLADE. Запоминающее устройство 12 является машиночитаемым носителем или устройством хранения программ, считываемым процессором 10. Процессор 10 может быть, например, микропроцессором, микроконтроллером, или процессором рабочей станции, или универсальной ЭВМ. Запоминающее устройство 12, которое хранит программу 16 цифровой производной давления, может быть накопителем на жестких дисках, постоянным запоминающим устройством (ПЗУ, ROM), запоминающим устройством на компакт-диске (CD-ROM), динамическим ОЗУ (DRAM) или другим оперативным запоминающим устройством (ОЗУ, RAM), флэш-памятью, магнитным запоминающим устройством, оптическим запоминающим устройством, регистрами (регистрирующим прибором) или другим энергозависимым и/или энергонезависимым запоминающим устройством. На фиг. 2 представлена блок-схема для "измерения параметра с шумами" 18. Измерение 18 с шумами представляет первую функцию. Специальный элементарный волновой сигнал 22 представляет вторую функцию. Специальный элементарный волновой сигнал 22 в этом описании будет описан ниже. Первая функция, представляющая измерение 18 с шумами, свернута в свертку 24 со второй функцией,представляющей специальный элементарный волновой сигнал 22. Свертка 24 описана в разделе 2.5 описания, выполняется в соответствии с уравнениями (16) или (17), представленными ниже. В результате свертки 24 генерируют выходной сигнал 20 высокого разрешения и высокой точности без шумов, который дает большее количество информации об измерении 18, вследствие отсутствия шумов. Хотя, вклю-4 008545 чавшие в себя шумы, данные измерения 18 воспроизводили данные, не интерпретируемые заказчиком,выходной сигнал 20 высокого разрешения и высокой точности без шумов может быть интерпретирован заказчиком, что описано ниже. Давление в скважине 26 (фиг. 3) может быть измерено. Если давление в скважине 26 измерено, генерируют частную функцию 18', представляющую измерение давления в нефтяной или газовой скважине, с шумами. Однако вследствие наличия шумов, частная функция 18' не может быть интерпретирована заказчиком. Тем не менее, частную функцию 18', представляющую измерение давления в нефтяной или газовой скважине, с шумами свертывают с производной 28 элементарного волнового сигнала (описана ниже) в свертку 24. Производную 28 элементарного волнового сигнала образуют на основании характеристики одиночной выборки ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. Т.е. производную 28 элементарного волнового сигнала формируют, используя ограниченное по полосе частот преобразование, соответствующее идеальному дифференцирующему устройству (cos(n/n), как описано в разделе 2.8). Коэффициенты элементарного волнового сигнала вычисляют с использованием способа Чебышева, используя алгоритм замен Ремеза. Первичными входными данными для алгоритма являются длина N фильтра и частота fc отсечки, которая является частотой, выше которой шумы являются основной составляющей полного сигнала. Для иллюстрации произвольно выбрана длина фильтра 60, хотя N может быть вычислено с использованием эмпирических формул. Свертка 24 (фиг. 3) представлена уравнениями (16) и (17) ниже. В результате свертки 24 генерируют имеющую намного более высокое разрешение производную 20 частной функции без шумов. Поскольку производная 20 частной функции не содержит шумов, то производная 20 частной функции, генерируемая в соответствии со сверткой 24, может быть интерпретирована заказчиком на этапе 30. На фиг. 4 представлена блок-схема, позволяющая осуществлять измерение, имеющее шумы, например, измерение давления с шумами в нефтяном или газовом резервуаре. Вследствие наличия шумов такое измерение не может быть интерпретировано заказчиком. Частная функция 18', представляющая выходной сигнал на основании некоторого измерения с шумами, такого как измерение давления в нефтяной или газовой скважине, свертывают с функцией 32 элементарного волнового сигнала в первую свертку 24 а. Когда частная функция 18' свернута с функцией 32 элементарного волнового сигнала в первую свертку 24 а, генерируют первый выходной сигнал, представляющий первую производную 20 а частной функции без шумов. Однако первая производная 20 а функции подвергается второй свертке с функцией 32 элементарного волнового сигнала во вторую свертку 24b. В результате формируют второй выходной сигнал, представляющий вторую производную 20b частной функции без шумов. Поскольку второй выходной сигнал не содержит каких-либо "шумов", как отмечено на этапе 34, получают информацию об измерении. Более подробное описание операций, представленных на фиг. 1, 2, 3 и 4, будет представлено ниже. Значительные объемы времени и денег были потрачены на научные исследования и разработку средств для измерения давления, имеющих высокое разрешение, включающих в себя измерение давления (например, в нефтяной или газовой скважине в резервуаре) и генерирование электронных выходных сигналов высокого разрешения и высокой точности, представляющих давление, выходные сигналы имеют точность или разрешающую способность до второго и третьего десятичного разряда. Эти электронные выходные сигналы высокого разрешения и высокой точности представлены как измерение 18 на фиг. 1, 2, 3 и 4. Когда появлялась необходимость использования измеренного давления, чтобы интерпретировать и дать предложения о том, как усовершенствовать скважину заказчика, и по производительности резервуара, информация, относящаяся к измеренному давлению, не могла быть использована, т.е. выходные сигналы высокого разрешения и высокой точности, имеющие разрешающую способность до второго и третьего десятичного разряда, не могли использоваться, вследствие наличия шумов в выходном сигнале давления. Т.е., с одной стороны, были затрачены средства на разработку измерительных средств высокого разрешения и высокой точности, а с другой стороны, полученные выходные сигналы высокого разрешения и высокой точности, имеющие разрешающую способность до второго и третьего десятичного разряда, не использовались, вследствие наличия шумов в выходном сигнале давления. В заявленном изобретении две технологии были объединены: (1) технология разработки измерительных средств для измерения давления, имеющих высокое разрешение и высокую точность, для использования в скважине, обеспечивающих обработку сигналов для выходных сигналов от измерителей, и(2) технология исследований и разработки резервуаров и практическое применение данных, полученных от этих измерителей. Таким образом, физика измерителей была объединена с физикой резервуаров. В результате в соответствии с настоящим изобретением был разработан алгоритм, в дальнейшем называемый программное обеспечение 16 цифровой производной давления, в котором, прежде чем отбрасывать и отвергать выходные сигналы высокого разрешения и высокой точности, имеющие разрешающую способность до второго и третьего десятичного разряда, содержащие шумы в выходном сигнале давления,эти выходные сигналы используют для дополнительной интерпретации резервуара. Программное обес-5 008545 печение 16 цифровой производной давления согласно настоящему изобретению не отвергает выходные сигналы давления высокого разрешения и высокой точности, имеющие точность или разрешающую способность до второго и третьего десятичного разряда, генерируемые измерителями давления, вследствие наличия шумов в выходном сигнале давления. Вместо этого программное обеспечение 16 цифровой производной давления согласно настоящему изобретению использует шумы на выходном сигнале давления,связанные с выходными сигналами давления высокого разрешения и высокой точности для интерпретации данных резервуара, поскольку на основании этих "шумов" может быть получено значительное количество информации. Программное обеспечение 16 цифровой производной давления согласно изобретению использует математические способы обработки сигналов, чтобы анализировать сигнал давления, выводимый от измерителей, программное обеспечение 16 цифровой производной давления согласно настоящему изобретению содержит "специальный способ" анализа шумов в выходном сигнале давления, связанных с выходными сигналами давления высокого разрешения и высокой точности, имеющими точность или разрешающую способность до второго и третьего десятичного разряда, чтобы получать более точную информацию о резервуаре. На фиг. 1-4, 37 и 38 выходные сигналы давления высокого разрешения и высокой точности, генерируемые измерителями давления, содержат много данных, имеющих разброс (т.е. "шум"), и в результате сигналы ранее нельзя было интерпретировать вследствие шумов в выходном сигнале давления. Однако программное обеспечение 16 цифровой производной давления согласно настоящему изобретению обеспечивает прием сигналов высокого разрешения и высокой точности, при этом ранее не интерпретируемые сигналы давления, содержащие шумы и имеющие точность или разрешающую способность до второго и третьего десятичного разряда (фиг. 37), можно обработать с помощью программы 16 обработки цифровой производной давления, т.е. согласно настоящему изобретению будет осуществляться "специальный способ" генерирования интерпретируемых, высокого разрешения и высокой точности выходных сигналов давления (фиг. 1-4), пример которых показан на фиг. 38. Интерпретируемые, высокого разрешения и высокой точности выходные сигналы давления, генерируемые по программе 16 цифровой производной давления, являются интерпретируемыми вследствие сглаженности кривой (фиг. 38). Сглаженность кривой означает, что выходной сигнал высокого разрешения и высокой точности не содержит шумов, и позволяет заказчику получать информацию, в большей степени относящуюся к существу вопроса. Сигналы давления, генерируемые измерителями (фиг. 37), не имеют какой-либо сглаженности кривой,что указывает на наличие шумов для сигналов давления, т.е. это сигналы давления, не интерпретируемые заказчиком."Специальный способ", осуществляемый на практике программой 16 цифровой производной давления согласно настоящему изобретению, обеспечивает вычисление производной давления, которое включает нижеследующие этапы. На фиг. 1-4 и 11 первым этапом "специального способа" является этап обработки сигнала, который включает создание специальной функции 22, 28 и 32 элементарного волнового сигнала. Функцию 22, 28 и 32 элементарного волнового сигнала создают в ответ на данные о резервуаре, например, минимальную и максимальную проницаемость резервуара, минимальную и максимальную длину для испытания скважины резервуара и другие общие рекомендации, имеющие отношение к резервуару. Если эти общие рекомендации, имеющие отношение к характеристикам резервуара, известны, вычисляют функцию 22, 28 и 32 элементарного волнового сигнала. Пример типичного элементарного волнового сигнала показан на фиг. 11. Данные, которые используют для создания функции 22, 28 и 32 элементарного волнового сигнала, раскрыты в таблице "Создание линейного фазового цифрового фильтра с конечной импульсной характеристикой (FIR), алгоритм замен Ремеза, длина фильтра дифференцирующего устройства равна 60,импульсная характеристика". Функция 22, 28 и 32 элементарного волнового сигнала является простой функцией, поскольку она является приближенно синусоидальной по характеру. Вторым этапом "специального способа" является этап 24, 24 а и 24b свертки. Уравнение свертки раскрыто в настоящем описании в виде уравнения (16) во временной области и в виде уравнения (17) в пространстве Лапласа. Свертка 24 двух функций временной области в пространстве Лапласа является весьма простой и предпочтительной, поскольку такая свертка требует простого умножения двух функций временной области. Функцию 22, 28, 32 элементарного волнового сигнала свертывают на этапе 24,24 а и 24b свертки с измерением 18 (включающем любые сопутствующие шумы), используя или уравнение (16), или уравнение (17). Если измерение 18 является откликом давления резервуара, то этап 24, 24 а,24b свертки для "специального способа" включает в себя этап осуществления свертки функции 22, 28, 32 элементарного волнового сигнала со второй функцией 18', представляющей отклик давления резервуара,включающий в себя любые сопутствующие шумы. Таким образом, формируют выходной сигнал 20 (фиг. 3), который не содержит сопровождающих шумов и который представляет функцию 18', являющуюся производной второй функции, представляющей отклик давления резервуара. Например, в фонтанирующей нефтяной или газовой скважине измеритель давления высокого разрешения и высокой точности используется для определения давления в скважине. Т.е. измеритель давления высокого разрешения и высокой точности используют, чтобы определять реакцию резервуара на-6 008545 изменение скорости потока. Измеряя эту реакцию, можно определить значительное количество информации о резервуаре, например, размер резервуара, сколько флюида находится в резервуаре, проницаемость резервуара, границы и другие важные параметры резервуара. Генерирование функции 22, 28, 32 элементарного волнового сигнала используется в электромеханике, теплопередаче и при диффузии лекарственного средства в кровотоке. Если программное обеспечение 16 цифровой производной давления настоящего изобретения осуществляет на практике "специальный способ", то функцию 22, 28, 32 элементарного волнового сигнала,сформированную в ответ на информацию о резервуаре, свертывают в свертку 24 и 24 а и 24b со второй функцией 18', представляющей отклик давления резервуара, включающий в себя шумы, чтобы генерировать и получать большее количество информации о резервуаре от измерителей давления, а именно, генерировать производную 20 второй функции 18', представляющей отклик давления резервуара. Однако"специальный способ", осуществляемый на практике программным обеспечением 16 цифровой производной давления согласно настоящему изобретению, также может использоваться для получения большего количества информации о других параметрах, отличных от отклика давления резервуара. Т.е. "специальный способ", осуществляемый на практике программным обеспечением 16 цифровой производной давления согласно настоящему изобретению, также может включать в себя свертку другой функции элементарного волнового сигнала с другой функцией, представляющей любое другое измерение, для получения большего количества информации о других параметрах, включенных в состав измерения или представляющих упомянутое измерение. Например, "специальный способ" может быть осуществлен на практике программным обеспечением 16 цифровой производной давления при определении сейсмических параметров. Т.е. в связи с деятельностью в сейсмической сфере "специальный способ" согласно настоящему изобретению будет включать в себя свертку 24 еще одной функции элементарного волнового сигнала, которая была сформирована при знании сейсмического отклика формации Земли, с еще одной функцией, представляющей сейсмическое измерение для получения большего количества информации о сейсмическом измерении, например, получить большее количество информации об отклике формации, когда источник взрывной или акустической энергии распространяет звуковые или акустические волны в формации Земли. Для большей конкретности, в связи с деятельностью в сейсмической сфере"специальный способ", осуществляемый на практике программным обеспечением 16 цифровой производной давления согласно настоящему изобретению, будет включать в себя свертку 24 функции элементарного волнового сигнала, созданной для измерения сейсмических волн или звука с сейсмическим измерением, включающим в себя шумы, чтобы генерировать, в конечном счете, выходную функцию, не содержащую шумов, которая даст возможность определить большее количество информации об отклике формации на звуковые или акустические волны, распространяющиеся в формации Земли. Следовательно "специальный способ", осуществляемый на практике программным обеспечением 16 цифровой производной давления согласно настоящему изобретению, включает в себя осуществление свертки специального элементарного волнового сигнала 22 с сигналом (фиг. 2), который представляет функцию, которая представляет измерение 18, включающее в себя шумы. Измерение 18 может быть любым сигналом, хотя в предпочтительном варианте осуществления (фиг. 3) измерение 18 является измерением давления в нефтяной или газовой скважине для нефтяного или газового резервуара, который содержит сопровождающие шумы. В предпочтительном варианте осуществления (фиг. 3) функция элементарного волнового сигнала является производной 28 элементарного волнового сигнала. При интерпретации давления используется производная давления, поскольку на основании производной может быть получена более точная информация. Если "специальный способ" осуществлен на практике программным обеспечением 16 цифровой производной давления согласно настоящему изобретению, вышеупомянутая производная 28 функция элементарного волнового сигнала по фиг. 3 является свернутой в свертку 24 в одном из вышеупомянутых уравнений (16) или (17) свертки с частной функцией 18', представляющей измерение давления в нефтяной или газовой скважине. В ответ на это, генерируют производную 20 этой частной функции без шумов. В результате "специальный способ", осуществленный на практике программным обеспечением 16 цифровой производной давления согласно изобретению, содержит свертку 24 производной 28 элементарного волнового сигнала с частной функцией 18' (и напоминание, что требуется производная этой частной функции), чтобы таким образом генерировать результат, который представляет намного более высокого разрешения производную 20 этой частной функции 18' без шумов. Этот результат можно интерпретировать, как отмечено на этапе 30 (фиг. 3), поскольку он не содержит "шумов". Следовательно, результат можно интерпретировать и передавать заказчику. Итак, когда измеряют давление, генерируют сигнал, который включает в себя "шумы". Этот сигнал, содержащий "шумы", свертывают в свертку 24,24 а, 24b с функцией 22, 28, 32 элементарного волнового сигнала и результат свертки 24, 24 а, 24b является гораздо более точной и намного более высокого разрешения производной 20 этого сигнала, которая не содержит шумов. Существенное отсутствие шумов от намного более высокого разрешения производной 20 этого сигнала означает, что намного более высокого разрешения производная 20 этого сигнала, может быть интерпретирована заказчиком. Пример гораздо более точной и намного более высокого разрешения производной 20 сигнала, которая не содержит шумов, представлен на фиг. 38.-7 008545 Следовательно, хотя обработка сигналов ранее осуществлялась отдельно от измерения, предложенный "специальный способ", осуществляемый на практике программным обеспечением 16 цифровой производной давления (фиг. 1), представляет собой комбинацию из обработки сигналов и измерения, причем измерение дополнительно включает в себя измерение давления. На фиг. 4 вторая производная давления, измеренного в нефтяной или газовой скважине, может выдавать даже большее количество информации о резервуаре. Однако вторая производная давления ранее не упоминалась в литературе, поскольку в функции второй производной содержатся "подавляющие шумы". В соответствии с еще одним аспектом настоящего изобретения "специальный способ", осуществляемый на практике программным обеспечением 16 цифровой производной давления согласно настоящему изобретению, теперь может быть расширен следующим образом. Применяют свертку дважды (фиг. 4), т.е. вначале осуществляют свертку частной функции 18' (фиг. 4), представляющей выходной сигнал на основании некоторого измерения (например, выходной сигнал измерителя давления, измеряющего давление в нефтяной или газовой скважине), с функцией 32 элементарного волнового сигнала первый раз, чтобы генерировать первый выходной сигнал, представляющий первую производную 20 а частной функции 18', а затем осуществляют свертку первого выходного сигнала, представляющего первую производную 20 а частной функции 18' с функцией 32 элементарного волнового сигнала второй раз, чтобы генерировать второй выходной сигнал, представляющий вторую производную 20b частной функции 18'. Вместо применения свертки к верхней кривой на фиг. 28, применяют свертку к нижней кривой на фиг. 28, которая представляет первую производную. На фиг. 4 для частной функции 18', представляющей давление от измерителя давления, осуществляющего измерения давления в нефтяном или газовом резервуаре, информация о резервуаре может быть получена на основании второй производной 20b частной функции 18', поскольку вторая производная 20b частной функции 18' не содержит вышеупомянутых "подавляющих шумов". Это весьма положительный результат, который получен посредством использования"специального способа", осуществляемого на практике программным обеспечением 16 цифровой производной давления согласно настоящему изобретению. Ниже раскрыты другие варианты способа и устройства СЦПД и устройства хранения программы согласно настоящему изобретению. Способ и устройство СЦПД могут генерировать временную или пространственную производную,не содержащую шумов, в других отраслях техники в дополнение к добыче нефти. Например, способ и устройство можно использовать в системах измерения и управления, когда необходимо знать скорость изменения, производную, или наклон (крутизну) измеренного параметра или входного сигнала относительно времени, относительно расстояния, или относительно другого параметра или переменной. СЦПД может применяться во всех случаях, где требуется математическая производная(ые) для набора данных или входного сигнала, и где требуется, чтобы выходные данные не содержали шумов. Кроме того, источником шумов могут быть погрешность измерения, ограничения чувствительного элемента или измерительного преобразователя (датчика), связанные с ним аппаратные средства или программное обеспечение обработки сигналов; другими словами, шумы могут быть либо внутренними, либо внешними для самого источника входных данных. Любые шумы, сопровождающие входной сигнал, или шумы, внесенные связанными аппаратными средствами или программным обеспечением обработки сигнала, обычно усилены традиционными способами получения производных, тем самым, нарушая выходные данные требуемой производной. Поскольку способ и устройство СЦПД согласно изобретению являются эффективными при формировании выходных данных, не содержащих шумов, они могут быть использованы в разных приложениях для значительного улучшения рабочей характеристики по сравнению с другими способами. Кроме того, способ эффективен всякий раз, когда требуемая программа алгоритма СЦПД и связанные с ним аппаратные средства обработки могут быть встроены или реализованы в пределах ресурсов запоминающих устройств, вычислительных и аппаратных средств обработки данных, которые содержит исходная система(т.е. везде, где могут быть использованы схемы по фиг. 1-4 для конкретного проекта). Для иллюстрации широкой области возможных применений, и их преимущества, несколько примеров приведены ниже. Примеры типа 1. В примерах типа 1 СЦПД формирует скорость и/или ускорение на основании измерений линейных данных, или координат, содержащих шумы для применения СЦПД однократно для скорости (фиг. 3) и для применения СЦПД дважды для ускорения (фиг .4). 1.1). Скорость каротажного кабеля в скважине, скорость намотанного шланга, индикатор скорости трубопровода и других трубопроводов, спускаемых в скважину/поднимаемых из скважины. СЦПД использует определение местоположения на основании дискретных отметок на кабеле, трубопроводе или трубе, соответственно, или от промежуточного ролика. Отметки могут быть сделаны любым физически чувствительным средством, т.е. механическим, электромагнитным или звуковым. Вторая производная СЦПД является входным сигналом на привод намотки кабеля или привод насосно-компрессорного трубопровода, чтобы ограничивать максимальное ускорение, а следовательно, максимальное напряжение на кабеле или трубопроводе. Преимущество: точное измерение и плавное управление скоростью намоточного барабана. Это уменьшает напряжение и вероятность повреждения кабеля или труб. 1.2). Подъемные устройства: СЦПД обеспечивает индикаторы скорости, использующие отметки-8 008545 дискретных позиций или измерения расстояний вдоль стены или кабеля, как в примере 1. Вторая производная СЦПД служит входным сигналом на контроллер привода подъемника, чтобы гарантировать безопасный плавный подъем, и свести к минимуму напряжения на оборудовании. 1.3). Воздушный летательный аппарат или самолет: СЦПД использует полученные глобальной системой (GPS) навигации и местоопределения данные координат, чтобы генерировать скорости в направлениях х, у или z. Преимущества: существенное сокращение ошибки скорости, что особенно необходимо при работе автопилота и в течение полуавтоматического или автоматизированного приземления. 1.4). Самолет: СЦПД использует полученные GPS данные, чтобы генерировать скорости подъема или подходящие скорости на основании полученных GPS данных координат. Преимущества: результатом является пассивная система, поскольку она требует только приема сигнала GPS и его обработку, но не требует никаких радиофизических или других электромагнитных излучений, таким образом, сводя к минимуму помехи передачи и перегруженность эфира, и для выполнения операций-невидимок. Она не требует внешних измерений давления (т.е. никаких трубок Пито). Она является независимой от пространственного положения самолета. 1.5). Самолет: СЦПД использует полученные радиолокационной станцией наземные данные высоты, чтобы генерировать скорость подъема/подходящую скорость, как упомянуто выше. 1.6). Предотвращение столкновения самолета: СЦПД использует данные радиолокационной станции для генерирования скорости столкновения с землей или с другим самолетом или преградами. Аварийная и управляющая система самолета будут использовать эту информацию в качестве входных данных, чтобы определить оптимальную стратегию предотвращения столкновения. 1.7). Управление транспортными потоками самолетов и предотвращение столкновения: местоположение каждого самолета, определенное системой GPS, может быть передано на наземную систему управления транспортными потоками самолетов, которая непосредственно использует СЦПД, чтобы определить вектор скорости каждого самолета и его скорость изменения высоты (полета). Результаты не содержат шумов, следовательно, они будут иметь более высокую точность и достоверность. Результаты в свою очередь могут быть использованы для вычислений предотвращения столкновения. 1.8). Предотвращение столкновения надповерхностного транспортного средства, т.е. автомобилей,автобусов, грузовиков, поездов, судов и т.д.: СЦПД использует либо радиолокационные, либо гидроакустические данные для генерирования скорости столкновения с другими транспортными средствами или преградами. 1.9). Подповерхностные транспортные средства (т.е. подводные лодки, дистанционнопилотируемые летательные аппараты (ДПЛА, RPV), торпеды и т.д.): СЦПД использует полученные гидроакустической станцией данные местоположения для генерирования скорости столкновения с другими транспортными средствами или преградами. 1.10). Станочные системы: СЦПД выдает сигнал индикатору скорости на основании определения координат, чтобы плавно управлять операцией резания и улучшения допустимого отклонения и чистовой обработки, а также сведения к минимуму потерь. 1.11). Автоматизированная сборка: СЦПД обеспечивает плавное измерение скорости и ускорения на основании данных позиционирования, имеющих шумы. При использовании в системе управления с обратной связью это минимизирует наведенные ускорением напряжения на деталях, таким образом,уменьшая риск поломки деталей и износа станка. Примеры типа 2. В примерах типа 2 СЦПД формирует угловую скорость и/или угловое ускорение на основании измерений угловых координат, содержащих шумы. Применение СЦПД однократно для угловой скорости (фиг. 3) и применения СЦПД дважды для углового ускорения (фиг. 4). При заданных, содержащих шумы данных угловых координат СЦПД формирует угловую скорость,не содержащую шумов. СЦПД формирует угловое ускорение, если применяется дважды. 2.1). Управление креном самолета и ракеты, углом наклона, курсом полета: СЦПД формирует не содержащие шумов вычисления угловой скорости самолета при заданных значениях измерений угловых координат от установленных внутри датчиков, таких как гироскопы, или внешних определений угловых координат самолета, таких как оптический датчик горизонта или оптическое средство астроориентации. Второе применение СЦПД генерирует информацию углового ускорения (фиг. 4) для систем управления вращением. Примеры типа 3. Автоматические системы управления. В автоматических системах или системах управления с обратной связью любая специфическая схема может рассматриваться в виде подмножества или специального варианта осуществления архитектуры общей схемы системы управления, называемой пропорционально-интегрально-дифференциальным регулятором (ПИД). При этом "дифференциальный" или "производный" относится к производной входного сигнала рассогласования (см. ссылку 61). Эта производная или ускорение рассогласования может обеспечить полезное демпфирование системы управления с обратной связью. Это может обеспечивать управление с опережением, которое позволяет минимизировать выходной сигнал. Однако в практическом варианте осуществления любые шумы в сигнале рассогласования, или возмущения, или ошибки в самой системе управления представляют серьезные проблемы для достижения преимуществ от регулирования по производной или по скорости. Типичная-9 008545 производная имеет характеристики фильтра верхних частот, который имеет тенденцию распространять, а иногда усиливать шумы и возмущения во всей системе. Применение способа и устройства СЦПД в этих системах позволяет улучшить рабочую характеристику при минимальных затратах. 3.1). Системы управления технологическими процессами: для регулирования температуры, давления жидкости или газа, скорости потока, или фазового регулирования. 3.2). Регулирование уровня жидкости. 3.3). Отопление, вентиляция и кондиционирование воздуха (HVAC): отопление, вентиляция и кондиционирование воздуха для системы управления печью и системы охлаждения. 3.4). Системы управления электропитанием: для регулирования напряжения, тока или частоты генератора. 3.5). Системы слежения радиолокационных станций, гидролокационных станций или телескопов. 3.6). Контроллер яркости для источников света или систем вывода данных на экран. 3.7). Системы наведения ракет, основанные на GPS преимущество в отсутствии электромагнитных излучений. 3.8). Системы управления для успокоителя волновой качки судов - использование скорости изменения (производной) гироскопической ориентации при уменьшении ошибок вследствие ухода гироскопа. 3.9). Робототехника: для управления движением и для систем датчика слежения и стабилизации. Примеры типа 4. Пространственные производные. 4.1). В проектах в геодезии и гражданском строительстве, где требуется наклон ландшафта или конкретного пути, но входная информация состоит из дискретных измерений положения, которые включают в себя шумы (т.е. ошибки). 4.2). Проектирование и анализ электромагнитных систем: в электромагнитном поле отображение пространственной производной указывает контуры электростатического поля. Способ СЦПД применяется с функцией времени, заменяемой пространственной переменной (т.е. координатами х, у или z относительно опорной системы координат). 4.3). Моделирование теплообмена и термодинамическое моделирование: это математическое моделирование требует вычисления скорости изменения температур в пространстве и во времени. СЦПД может минимизировать влияние шумов в смысле вычислительных ошибок. 4.4). Прогнозирование погоды: СЦПД может улучшать анализ штормов, а также моделирование и имитацию синоптических ситуаций, поскольку они используют пространственные производные температуры и давления по времени и пространственному местоположению (см. ссылку 62). Подробное описание предпочтительного варианта осуществления изобретения 2. Теоретические соображения. Ниже приведены основные элементы цифровой обработки сигналов, необходимые при разработке способа цифровой производной давления (СЦПД). Более полное раскрытие приведено в ссылках 18-38. 2.1. Касательно частотной области. Большинство специалистов по обработке сигналов согласятся с тем, что нигде не раскрыты основополагающие преимущества обработки данных в частотной области над временной областью. Однако следует обратить внимание на частотную зависимость данных. Важно отметить, что в каждом домене содержится одинаковая информация, можно просто дать более информативную оценку интерпретируемых данных. С этой точки зрения, частотная область является аналогичной области Лапласа; специалистам более известно связанное интегральное преобразование давления. Несколько понятий, таких как разрешающая способность, повторяемость, отношение сигнал-шум и систематическая погрешность, могут быть легче визуализированы в частотной области, чем во временной области. Тогда как имеется ряд преимуществ рассмотрения данных неустановившегося давления в частотной области, наиболее важным является возможность определения отношения сигнал-шум; зная, что выше некоторой граничной частоты будут наблюдаться только шумы (т.е. нерезервуарные явления). В нижеследующих разделах обсуждаются понятия, касающиеся рассмотрения измеренных данных давления в частотной области, что предпочтительнее, чем во временной области. 2.2. Выборки давления и z-преобразование. Для последовательности из n измерений давления в равномерно разнесенные (равноотстоящие) интервалы времени t могут быть записаны в виде при этом временами выборок являются Пусть интервал t является постоянным, тогда z-преобразование для последовательности р[n] в уравнении (1) определяется в виде суммы где z является комплексной переменной. Отношение, заданное правой частью уравнения (3), иногда называют прямым z-преобразованием, поскольку оно преобразует сигнал р(n), соответствующий времен- 10008545 ной области, в его представление P[z] в комплексной плоскости. Z-преобразование играет важную роль при анализе дискретных сигналов. Оно играет такую же роль при анализе дискретных функций, какую преобразование Лапласа и Фурье играют при анализе непрерывных функций. Т.е. оно значительно упрощает анализ и создание анализа дискретных сигналов посредством преобразования конечноразностного уравнения в алгебраическое уравнение. Функции р[n] и P[z] образуют пару z-преобразования, обозначаемую в виде Можно рассмотреть, например, одну выборочную последовательность или дельта-последовательность Тогда из определения по уравнению (4) z-преобразованием для одиночной выборки является Другой важной функцией является дельта-последовательность со сдвигом во времени Ее z-преобразование следует из уравнения (7) и определение дается в соответствии с уравнением (3) в видеz-преобразованием одного выборочного значения p(n-k) давления, измеренного в момент времени (n-k)t,является С математической точки зрения z-преобразование является просто альтернативным представлением сигнала. Это подробно проиллюстрировано в вышеупомянутом примере (уравнения 5-9), в котором коэффициентом z-n в заданном преобразовании является значение сигнала в момент времени n. Другими словами, показатель степени для z содержит временную информацию, необходимую, чтобы идентифицировать выборочные значения сигнала. Во многих случаях можно выразить сумму конечного или бесконечного ряда для z-преобразования в аналитическом виде. В таких случаях z-преобразование предлагает компактное альтернативное представление сигнала, описано ниже. 2.3. Цифровая передаточная функция. Если входными данными х[n] и выходными данными y[n] являются последовательности цифровой(дискретной) системы, и они являются связанными согласно линейному разностному уравнению, которое имеет постоянные коэффициенты, то может быть использована 18 нижеследующая запись Используя понятия из предыдущего раздела, можно взять z-преобразование для обеих частей уравнения (10) (пренебрегая начальными условиями), чтобы получить Цифровую передаточную функцию тогда определяют в виде Следовательно, выходные данные являются произведением входных данных, которые умножены на цифровую передаточную функцию, т.е. В качестве альтернативы, передаточная функция может быть вычислена как z-преобразование для реакции или отклика системы на одно импульсное возмущение. Подход передаточной функции используется во многих дисциплинах, особенно относящихся к электромеханическим системам и системам обработки сигналов. Методика передаточной функции, примененная к измерению давления при испытании скважин, раскрыта в Veneruso et al.9 Эта методика является мощным инструментальным средством, которое математически описывает процесс измерения испытания скважины; т.е. оно связывает сигнал отклика на выходе измерителя с его входным давлением и,возможно, температурой. Зная эти связи, специалист может более точно проектировать испытания скважины на основании ожидаемого отклика резервуара и известных характеристиках измерителя, таких как уход параметров, разрешающая способность, влияние температуры и т.д. Схема того, как передаточная функция используется при создании и анализе кривых восстановления давления, показана на фиг. 5. Понятие передаточной функции позволяет вычислять и надлежаще интерпретировать ошибки измерения,- 11008545 внесенные в данные неустановившегося давления. Учет этих ошибок сводит к минимуму риск ложной интерпретации ошибок измерения в качестве свойств резервуара. 2.4. Теорема дискретизации. Для каждого интервала дискретизации t существует характеристическая частота fN, называемая частотой Найквиста. Частота Найквиста связана с интервалом дискретизации следующим простым соотношением Если непрерывная функция p(t), которая дискретизирована в интервале At, ограничена частотами,меньшими по абсолютному значению, чем fN, то функцию p(t) можно полностью представить посредством ее выборочных значений. Это имеет замечательные последствия, особенно в областях сжатия данных и систем сбора данных скважинного записывающего устройства, поскольку можно представлять непрерывный сигнал посредством намного меньшего набора разнесенных выборочных значений. Надлежащее разнесение связано с частотным спектром сигнала и конкретно с частотой Найквиста. С другой стороны, если сигнал не ограничен частотами ниже частоты Найквиста, оказывается, что спектральная информация, которая находится вне частотного диапазона -fNffN, является свернутой обратно в этот диапазон и избирательно изменяет спектральное содержание в пределах этого диапазона. Это явление называется наложением спектров при дискретизации. Любая частотная составляющая вне диапазона частоты Найквиста (-fNffN) является наложенной на этот диапазон в соответствии с недостаточной частотой дискретизации. Наложение спектров проиллюстрировано на фиг. 6. Наложения спектров (фиг. 6). Немного более ясное пояснение теоремы дискретизации, взятое из Proakas и Manolakis18, изложено ниже. Если самая высокая частота, содержащаяся в аналоговом сигнале x(t), является fmax=B, и сигнал дискретизирован с частотой fs2fmax=2B, то x(t) может быть точно восстановлен на основании его выборочных дискретных значений, используя интерполирующую функцию. Частота дискретизации fN=2B=2fmax называется частотой Найквиста. Т.е. частота Найквиста является пределом дискретизации, ниже которого первоначальный сигнал не может быть однозначно восстановлен на основании выборок. 2.5. Свертка. Понятие свертки является самым основным и для цифровой обработки сигналов, и при испытании скважины. Что-либо столь основное обязано иметь несколько определений, и это справедливо для свертки. Возможно, самым легким способом определения свертки является определение сначала ее математического "родственника" - корреляции. Корреляция является мерой того, насколько два сигнала или измерения имеют сходство между собой, или в качестве альтернативы мерой величины, до которой один сигнал может рассматриваться в качестве линейной функции другого. Свертка является корреляцией с одним из сигналов, обратным по направлению и сдвинутым на требуемое количество выборок. В дискретной форме операция свертки может быть выражена следующим образом: Уравнение (15) часто упоминается как суммирование суперпозиций. Для непрерывных сигналов суммирование заменяют интегрированием. В анализе испытания скважины, например, представляет интерес выполнение свертки давления и скорости потока где q является глубинной или забойной скоростью потока;p'wf является производной гидродинамического забойного давления при постоянной скорости;pwf(t) является гидродинамическим забойным давлением с учтенным изменением скорости. В данном исследовании будет использоваться уравнение (15), если упоминается свертка. Свертка имеет много свойств, она является коммутативной, ассоциативной и дистрибутивной. Наиболее важным свойством для рассматриваемых целей является то, что две функции (или сигналы) могут быть свернуты в пространстве преобразования (Фурье-, Лапласа- и z-преобразования) посредством простого умножения. Т.е. для случая функций Много других полезных свойств свертки могут быть найдены в работе Churchill39. 2.6. Цифровые фильтры. Фильтрацией является процесс, посредством которого спектр частот сигнала может быть изменен,может приобрести новую форму (восстановлен), или можно управлять в соответствии с некоторым требуемым техническим условием. Это может повлечь за собой усиление или ослабление (затухание) диапазона частотных составляющих, подавление или выделение одной конкретной частотной составляющей и т.д. Цифровой фильтр является фактически цифровой системой, которая может использоваться, чтобы- 12008545 фильтровать дискретные сигналы. Цифровой фильтр может быть реализован либо аппаратными средствами системы, либо в виде программного компонента. Фильтры также будут реализованы в виде программного обеспечения, хотя, как указано ниже, не запрещено использовать алгоритм СЦПД в программно-аппаратном средстве запоминающего измерителя. Цифровые фильтры могут быть разделены и подразделены на многие категории. Будет обсужден только специальный класс фильтров, используемых в СЦПД - "причинно-следственный" фильтр с конечной импульсной характеристикой (КИХ). Фильтр КИХ, вследствие способа его осуществления, часто называют нерекурсивным фильтром или фильтром свертки. На основании представления данной операции во временной области, фильтр КИХ иногда называют фильтром скользящего среднего. Длительность(или длина последовательности) импульсной характеристики этих фильтров является по определению конечной. Следовательно, выходной сигнал может быть записан в виде конечной суммы свертки где x(n-m) является входными данными,h(m) является импульсной характеристикой длины N (последовательностью из N откликов). Передаточная функция фильтра КИХ задается как z-преобразование для h(m) в виде Частотную характеристику фильтра находят просто подстановкой z=ej, что дает гдеявляется частотой в радианах в секунду. Строго говоря, показателем степени должен быть jtm,при этом t является интервалом времени между интервалами шкалы целого для m, т.е. интервалом дискретизации. Предполагается, что t является постоянным для всех (далее в разделе 3.1 это ограничение будет снято). Частотав радианах в секунду также может быть выражена в герцах (периодов в секунду,Гц, f). Эти величины связаны Основной задачей создания фильтра КИХ является определение оптимального значения N, числа одночленов h(m), и значений h(m), чтобы достичь требуемого воздействия на входной сигнал. Требуемым воздействием является получение идеальной производной входного сигнала - давление в зависимости от времени. 2.7. Традиционные алгебраические дифференцирующие устройства. С точки зрения передаточной функции дифференцирующее устройство является системой, выходным сигналом которой является взятая по времени производная ее входного сигнала, например, если входной функцией является тогда выходным сигналом является Этот простой пример в дополнение к обеспечению удобного входа в частотную область обеспечивает новое понимание наряду с некоторыми мощными аналитическими средствами. Например, передаточная функция идеального дифференцирующего устройства по фиг. 7 имеет частотную характеристику,которая является линейно пропорциональной частоте и имеет постоянный фазовый сдвиг 90. Ниже описаны традиционные дифференцирующие устройства, использующие такой же подход; т.е. рассмотрение линейности абсолютного значения для частотной характеристики. Частотная характеристика идеального дифференцирующего устройства (фиг. 7). Обычным способом вычисления численных производных является способ Ньютона с использованием двух точек, заданный в соответствии с Задача этого способа ясно показана на фиг. 8 - это фильтр верхних частот. Точки на фиг. 8 были вычислены посредством нахождения n-точечной амплитудно-частотной характеристики H(ejw), цифрового фильтра, определяемого в соответствии с разностным уравнением (24). Фильтр аппроксимирует идеальное дифференцирующее устройство только на очень низких частотах, ниже 0,2 от частоты Найквиста. На более высоких частотах его поведение приближается к усилителю с коэффициентом усиления два. Такое поведение можно объяснить со ссылкой на фиг. 9. На низких частотах (относительно частоты Найквиста) точки А и В выборки находятся близко друг к другу, следовательно, их разность близко аппроксимирует производную синусоиды. Чтобы увидеть это математически, пусть при этом t является бесконечно малым. Следовательно, На высоких частотах (близко к частоте Найквиста), точки дискретизации имеют более широкое разнесение, например, точки С и D. Их разность приблизительно вдвое больше амплитуды синусоиды. Поэтому выходной сигнал имеет коэффициент усиления до двух. Математически имеем Следовательно, Дискретизация для традиционных дифференцирующих устройств (фиг. 9). Другой широко известный способ численного вычисления производных (численного дифференцирования) задается в соответствии с формулой Стирлинга для центральной разности Этот способ аппроксимирует идеальное дифференцирующее устройство только на очень низких частотах, как в способе Ньютона. Амплитудно-частотная характеристика для формулы Стирлинга центральной разности представлена на фиг. 10. Точки дискретизации для этого способа заданы точками С и Е на фиг. 9. Сравнения производных Стирлинга и идеальных (фиг. 10). Чтобы подвести итог, тогда как способ Ньютона двухточечной разности является лучшим соответствием для идеального дифференцирующего устройства (фиг. 8), формула Стирлинга центральной разности является очень полезной, если желательно затухание высоких частот. 2.8. Идеальное цифровое дифференцирующее устройство. Как упомянуто выше, идеальное дифференцирующее устройство имеет частотную характеристику,которая является линейно пропорциональной входной частоте. Подобным образом идеальное цифровое дифференцирующее устройство определяют как такое, которое имеет частотную характеристику Характеристикой одиночной выборки, соответствующей Н, является Характеристика одиночной выборки является антисимметричной, т.е. h(n)=-h(-n). Следовательно,h(0)=0. Идеальным цифровым дифференцирующим устройством является просто фильтр длины N со значениями h(n), являющимися коэффициентами фильтра. Известны многочисленные способы вычисления этих коэффициентов, описание не приводится, что раскрыто в ссылках 18, 19 и 20. Способ создания фильтра, используемый в данном изобретении, сформулирован в виде задачи аппроксимации Чебышева. Данный подход является оптимальным способом создания в том смысле, что взвешенная погрешность аппроксимации между требуемой частотной характеристикой и фактической частотной характеристикой равномерно рассеяна по диапазону частот. Способ аппроксимации Чебышева наиболее точен, но не обязательно наиболее эффективен в терминах требуемого времени центрального процессора (ЦПУ, CPU). Есть более простые способы, такие как способ 18 взвешивания и способы 18,19 частотной дискретизации. Эти способы относительно просты, однако, они имеют недостатки, если применяются общим образом. В данном изобретении способ Чебышева был выбран, прежде всего, за его точность. Способ аппроксимации Чебышева для создания идеального дифференциального фильтра включает в себя решение системы линейных уравнений вида где L является числом экстремальных частот n; параметры ck иопределяют посредством решения системы уравнений, используя способ, известный как алгоритм 40 замен (переменных) Ремеза. Входными данными для этого алгоритма являются проектные характеристики фильтра: длина фильтра N, требуемая полоса частот (частота отсечки fc) и максимально допустимая относительная погрешностьаппроксимации. Значение частоты отсечки может быть определено непосредственно данными давления, как поясняется в разделе 2.10. На фиг. 11 показан алгоритм замен Ремеза, изложенный в работе Parks и McClellan41, и осуществленный в программном обеспечении, описанном в разделе 3.6. Пример создания дифференцирующего устройства, использующего этот алгоритм, приведен ниже. При этом длина фильтра составляет 60, частота отсечки составляет 0,1, и максимальная (полоса задержки) частота равна 0,15. Коэффициенты показаны графически на фиг. 11. Частотная характеристика для коэффициента элементарного волнового сигнала показана на фиг. 8. Абсолютная величина пропорциональна частоте до тех пор, пока не достигнута частота отсечки fc=0,1. Конечная импульсная характеристика (КИХ) Создание цифрового фильтра с линейной фазовой характеристикой Алгоритм замен ремеза Дифференцирующее устройство Длина фильтра =60 Импульсная характеристика Коэффициент элементарного волнового сигнала на основании алгоритма замен Ремеза (фиг. 11). Частотная характеристика коэффициентного элементарного волнового сигнала по фиг. 11 представлена на фиг. 12. 2.9. Автокорреляция. Корреляция, как отмечено выше, является просто мерой подобия. Корреляцию сигнала, например,x(t) с самим собой называют автокорреляцией. Функция автокорреляции, несмотря на то, что не используется непосредственно в этой работе, представлена кратко для последующего описания спектральной плотности мощности. Функция автокорреляции Rx является мерой подобия между x(t) и его задержкой x(t+). Например, если Rx является большим положительным числом, то х имеет строгое сходство с x(t+). Сле- 15008545 довательно, изменения в x(t) будут отражены в пропорциональных изменениях в x(t+). Если RX имеет большое отрицательное значение, это подразумевает, что изменения в х обратно пропорциональны изменениям для x(t+). Наконец, Rx, имеющее значение нуль, означает, что х и x(t+) имеют, в среднем, очень немного общего. Имеется другая, менее очевидная интерпретация корреляции. Если для некоторого t, Rx является большим, х имеет тенденцию повторять себя каждые t секунд (или выборок). Т.е. х будет иметь периодическое поведение с частотой 1/t Гц. Следовательно, имеется связь между функцией автокорреляции и частотной областью. 2.10. Спектральная плотность мощности. Представление в частотной области частоты для функции автокорреляции называют спектральной плотностью (СПМ, PSD) мощности или спектром мощности. Спектр мощности сигнала x(t) является мерой энергии или мощности, содержащейся в x(t), на каждой частоте. Анализ спектра мощности сигнала можно использовать, чтобы определить местоположения частоты, в которых находятся энергия, или сигнал, или шум. Спектральная плотность мощности использована, чтобы определить, на какой частоте сигнал резервуара становится незначащим по сравнению с полным измеренным сигналом. Более точно,спектральная плотность мощности будет задавать частоту отсечки, требуемую алгоритмом замен Ремеза. Частота отсечки является, возможно, наиболее важным фактором в создании фильтра элементарного волнового сигнала и по этой причине можно обосновать способ вычисления, используемый в данном описании для вычисления спектральной плотности мощности. Спектральная плотность мощности может быть вычислена множеством различных способов. Простые способы включают в себя (1) вычисление быстрого преобразования (БПФ, FFT) Фурье для автокорреляции сигнала и (2) умножение БПФ на комплексно сопряженное значение сигнала. Основные ссылки по спектральной оценке включают: Bartlett42, Blackman и Tukey43, Grenander и Rosenblatt44 и Hannan45. Более современные ссылки: Jenkins и Watts46 и Koopmarms47 или Press, et al.48 Проблема вычисления спектральной плотности мощности состоит в том, что это не имеет определенного способа. Чтобы вычислить СПМ аналитически, требуется большее количество информации от сигнала, чем обычно доступно. Поэтому большинство способов использует теорию оценок и эмпирические предпосылки, получаемые на основании практического опыта. Наиболее современные (компьютеризированные) способы вычисления СПМ используют график спектральной функции, или периодограмму. Периодограмма является просто оценкой спектра плотности мощности, оцениваемой с использованием упомянутой выше методики, соответствующей вычислению преобразования Фурье для оценки автокорреляции Rx. Математически периодограмму IN определяют в виде В целом, оценка периодограммы не является согласованной оценкой спектра, и ее поведение становится ошибочным по мере того, как длина N последовательности увеличивается. До некоторой степени общепринятый подход к уменьшению дисперсии оценок периодограмм состоит в том, чтобы составить среднее значение по некоторому количеству независимых оценок. Применение такого подхода к оценке спектра раскрыто в работе Bartlett42. В этом подходе последовательность данных х(n), 0nN-1 разделяют на К сегментов из М выборок каждый, так что N=KM, формируют сегменты и вычисляют К периодограмм Оценку спектра определяют в виде Сложность этого способа состоит в том, что для фиксированной длины последовательности по мере увеличения количества периодограмм уменьшается дисперсия, но М также уменьшается, и, следовательно, уменьшается разрешающая способность спектра. Таким образом, имеется компромисс между разрешающей способностью спектра (систематической ошибкой) и дисперсией оценки. Кроме того, подбор М и N обычно осуществляют посредством проб и ошибок или из предшествующих данных рассматриваемого сигнала. В работе Welch49 представлена модификация процедуры, предложенной Bartlett, которая устраняет дилемму оптимизации точности за счет разрешающей способности. Этот способ непосредственно использует БПФ и легко программируется. Этот способ использован в данной работе в программном обеспечении, описанном в разделе 3.6. Устойчивый способ по Welch использован, чтобы вычислять спектральную плотность мощности для нескольких обычных моделей резервуара. Цель состоит в том, чтобы определить чувствительность и связь, если таковая имеется, для СПМ по отношению к измеренному отклику давления при испытании- 16008545 скважины. Понятно, что использование аналитических решений предотвращает влияние шумов измерения на СПМ, и подход к этой проблеме представлен ниже. В этом разделе представляет интерес рассмотрение влияния отклика модели на СПМ. Далее в разделе 3.4 будет показано, как использовать вычисленную СПМ, чтобы обеспечить входные данные для алгоритма СЦПД. Рассматриваемыми моделями являлись:(1). Совершенная по степени вскрытия скважина, конечный радиус, без WBS - гомогенная - бесконечная;(2). Совершенная по степени вскрытия скважина, конечный радиус, без WBS - двухпористая-PSS бесконечная;(3). Совершенная по степени вскрытия скважина, конечный радиус, c/WBS - гомогенная - бесконечная;(4). Совершенная по степени вскрытия скважина, конечный радиус, c/WBS - гомогенная - замкнутый круг. Безразмерные отклики давления для каждого случая были вычислены в области Лапласа при постоянном, единичном интервале и были численно вставлены во временную область, используя алгоритм,данный в работе Stehfest7. Спектральная плотность мощности была вычислена для каждого отклика, используя способ Welch. Результаты представлены на фиг. 13. По анализу диаграмм на фиг. 13 можно вывести два заключения. Первым является то, что СПМ в целом весьма нечувствителен к поведению скважины/резервуара. Это хорошо, поскольку редко известно поведение системы заранее. Знание, что СПМ будет иметь тот же самый характер независимо от модели скважины/резервуара, позволяют уверенно отличать сигнал резервуара от шумов. Вторым заключением является то, что более значительная часть энергии (или мощности) содержится в диапазоне весьма низкой частоты. Это согласуется с интуицией. Ожидают, что резервуар должен иметь более низкую частотную характеристику, чем шумы в системе, вследствие, например, вибрации измерителя. На основании фиг. 13 можно осторожно вывести заключение, что вне нормированной частоты 0,4 в полном сигнале будут, наиболее вероятно, преобладать шумы. 3. Практические соображения. До сих пор были рассмотрены только идеальные ситуации данных, дискретизированных с постоянным интервалом или равномерно, для аналитических функций с регулярным поведением. Сложной задачей, на которую направлены нижеследующие разделы, является применение предварительно обсужденных понятий к реальным ситуациям неравномерно дискретизированных измерений давления, к данным,которые многократно содержат артефакты сбоев измерителей, фазового поведения, изменяющейся скорости потока и т.д. Подчеркивается важность отделения этих физических воздействий от более тонких неточностей, свойственных процессу измерения, таких как недостаточное разрешение, наложение спектров, эффект передачи, явления отбрасывания, цифровые шумы, эффект дифференцирования и т.д. 3.1. Вычисление СЦПД. Прежде, чем приблизиться к практическим задачам, с которыми сталкиваются при применении СЦПД к данным испытания скважины, будет подведен итог для вычислительной процедуры, используя простой пример синусоидальной волны со случайным (белым) шумом, добавленным для иллюстративных целей. Входная функция задается в виде где t = от 0 до 300 с и функция rand формирует случайные числа между 0 и 1, всякий раз повторно порождаемые с текущим значением t. Диаграмма уравнения (46) вместе с конечно-разностной производной представлена ниже на фиг. 14 (производная была сдвинута вертикально, чтобы согласовать общий масштаб). Входной сигнал и конечно-разностная производная (фиг. 14). Этапами вычисления цифровой производной давления являются нижеследующие. 1. Создают элементарный волновой сигнал, используя ограниченное по полосе частот преобразование, соответствующее идеальному дифференцирующему устройству (т.е. cos(n)/n), как описано в разделе 2.8. Коэффициенты элементарного волнового сигнала вычисляют с использованием способа Чебышева, используя алгоритм замен Ремеза. Первичными входными данными для алгоритма являются длина N фильтра, и частота fc отсечки, выше которой шумы являются основной составляющей полного сигнала. Для иллюстрации произвольно выбрана длина фильтра 60, хотя значение N может быть вычислено с использованием эмпирической формулы. 2. Определяют частоту отсечки, вычисляя спектральную плотность мощности сигнала и выбирая частоту, на которой энергия сигнала становится минимальной. В этом примере, поскольку известно, что истинным сигналом является синусоидальный сигнал, можно точно выбрать этот минимум, отмечая частоту, в которой спектр истинного сигнала отклоняется для сигнала с шумами. Сравнение спектра сигнала показано на фиг. 15. Частотой отсечки является fc=0,055. 3. Используя эти значения в качестве входных данных, результирующие коэффициенты h(m) свертывают с входным сигналом по каждой выборке в момент времени t, чтобы сформировать цифровую- 17008545 производную d(signal)/d(t) Результирующая СЦПД показана на фиг. 16. Сравнение спектров сигнала и сигнала + шумы (фиг. 15). Сравнение конечно-разностной производной с СЦПД (фиг. 16). 3.2. Вопросы дискретизации данных. В литературе по ЦОС в неявной форме полагают, что сигнал был дискретизирован при постоянном и единичном интервале. До сих пор подобным образом рассматривался только упрощенный сценарий, в котором давление измеряют в постоянном и единичном интервале выборки по оси времени. При испытании скважины такая идеализированная частота дискретизации встречается редко. Во многих случаях сложные измерители давления осуществляют выборку значений на основании изменения давления между двумя возможными временными показателями. В других случаях данные могут быть дискретизированными с постоянным интервалом, с постоянной частотой, только должны быть прорежены впоследствии на стадии интерпретации или обработки. Необходимо также рассмотреть ситуацию, в которой последовательные точки данных пропущены вследствие отказа измерителя. Чтобы полностью обобщить алгоритм СЦПД, необходимо рассмотреть разнообразные возможные неоднородные схемы дискретизации. Исчерпывающий литературный поиск дает несколько подходов к вычислению спектральной плотности мощности для неравномерно дискретизированных данных. Способ, используемый в данном описании, взят из работы Press et al48. Для дополнительного, менее строгого способа можно использовать работу Childers37. В работе Press, et al. в основном видоизменено более раннее решение, данное в работеLomb51 и расширенное в работе Scargle52. Способ Lomb"a оценивает данные только в моменты времени ti,которые являются измеряемыми. Пусть, например, имеются N точек данных hi=h(ti), i=1, , N. Среднее и дисперсию данных находят, соответственно, согласно формулам и Нормированная периодограмма согласно Lomb определена в соответствии с Постояннаяявляется сдвигом, который делает PN полностью независимым от сдвига всех из ti на любую постоянную. Как только нормированная периодограмма PN вычислена, может использоваться алгоритм согласно Welch точно так же, как в разделе 2.10, чтобы оценить спектральную плотность мощности. Но осуществление способа Lomb/Welch является прямым, алгоритм является намного более медленным, чем алгоритм для равномерно разнесенных данных. Вычисление СЦПД для неравномерно дискретизированных данных. В случае постоянной, но неединичной частоты дискретизации, вычисленная СЦПД может быть просто нормирована относительно временного интервала. Т.е. В случае неоднородного интервала дискретизации решение не является таким прямым. Одним довольно очевидным решением является просто интерполирование заданной временной совокупности по сетке постоянных интервалов и продолжение с использованием уравнения (52). Эта методика имеет несколько недостатков, не последним из которых является создание точек ложных данных. Кроме того,непосредственно интерполирование независимо от способа вносит ошибку, которая будет увеличена после дифференцирования. Решение, которого добивались первоначально, было следующим: вычислить коэффициенты элементарного волнового сигнала обычным образом, используя алгоритм замен Ремеза, как описано в разделе 2.8. Набор результирующих коэффициентов затем может быть уточнен соответствующей простой периодической функцией. Результирующая функция может использоваться, чтобы вычислить коэффициенты, требуемые при соответствующем разнесении, совместимом с разнесением измеренных данных. В качестве примера, можно рассмотреть измерение давления на фиг. 17. Данные давления с логарифмической выборкой (фиг. 17).- 18008545 Точки логарифмически распределены во времени, что является обычным при сборе данных давления в переходном режиме при заданном логарифмическом поведении процесса диффузии давления. Кроме того, аналитические решения уравнения диффузии, которое также должно быть дифференцировано для согласования типов кривых, обычно вычисляют по логарифмической временной сетке. В данном примере величины давления были вычислены с использованием уравнения (42) по логарифмической временной сетке из 50 точек на цикл (интервал времени). Коэффициенты Ремеза, следующие из этого временного распределения, показаны на фиг. 18. Равномерно и логарифмически разнесенные коэффициенты Ремеза (фиг. 18). Эта методика изящна с точки зрения обработки сигналов и дает надежные результаты, если данные не являются слишком неравномерно дискретизированными; т.е. если нет больших расхождениий между выборками. Однако этот подход требует, чтобы новый набор из N коэффициентов был вычислен для каждой точки давления p(i), используя N/2 предыдущих точек и (N/2)-1 последующих точек в качестве входных данных для уравнения многочлена. Результатом является то, что алгоритм требует слишком много времени для диалоговой интерпретации. Для общего случая было найдено, что простое расширение уравнения (52) посредством использования подходящих разностей времен дает очень точные результаты Этот подход легче трактуется с точки зрения осуществления, является гораздо более эффективным,и применим независимо от схемы осуществления выборки данных. Этот подход будет использован при вычислении примеров в разделе 3.5. 3.3. Объединение различных функций времени. Первоначально, производной давления согласно работе Bourdet et al. являлась просто dp/dt. Это самая простая из производных для выполнения, и она математически удовлетворительна, посколькуdp/dt появляется непосредственно в уравнении диффузии для неустановившегося потока. Логарифмическое решение уравнения диффузии предлагает взятие производной dp/dln(t) или (dp/dt)(t). Эта модификация имеет преимущество формирования распознаваемого, отличительного наклона графика при вычерчивании по логарифмической сетке. В последнее время популярно (судя по широкому использованию в коммерческом программном обеспечении) дифференцировать по характеристической временной функции для рассматриваемого неустановившегося потока. Например, более легко визуально идентифицировать нулевой наклон, чем наклон, скажем, одной четвертой. Чтобы идентифицировать билинейный поток в наборе данных для трещиноватой скважины, можно взять производную dp/dt0,25 для формирования горизонтального направления в режиме билинейного потока. Точно так же производные dp/dt0,5 иdp/dt-0,5 сформируют направления нулевого наклона для линейного и сферического потоков, соответственно. Любой другой режим потока, представляющий интерес для рассмотрения, может быть различим посредством взятия подходящей производной функции. Общие режимы потока и характеристики их характеристических производных показаны ниже на фиг. 19. Общие режимы потока (фиг. 19). Последней временной функцией, которую необходимо рассмотреть, и возможно наиболее важной,является функция суперпозиции времени. Это временное преобразование учитывает влияние периодов потока, предшествующих анализируемым, и применимо для ситуаций, в которых поведение резервуара является постоянным от одного переходного режима до следующего, т.е. линейных систем. В большинстве ситуаций, с которыми сталкиваются при испытании скважин, строго придерживаются ограничения линейности. Примером нелинейной ситуации является последовательность нагнетания-спада при испытании нагнетательной скважины. Очевидно, фронт закачиваемого флюида не будет постоянным во время нагнетания, и таким образом использование методики суперпозиции для анализа с переменной скоростью не будет действительным. Однако было показано 53, что нелинейность, являющаяся следствием перемещения фронта от одного периода к следующему, является достаточно слабой, так что можно использовать обычные методики анализа (суперпозиция). С точки зрения интерпретации, необходимо включить функцию суперпозиции в состав СЦПД, чтобы обеспечить анализ с переменной скоростью обычным образом, чтобы все ситуации могли быть обработаны. Это должно быть выполнено таким способом, в котором используются принятые методики суперпозиционного анализа, уже имеющиеся в программном обеспечении анализа испытания скважины. На основании принципа суперпозиции 54 для t=t-tn и заданной последовательности из n этапов изменений в поверхностной скорости потока, qj=(qj+1-qj), для j=1, , n, при q0=0, забойное давление задается в соответствии с При этом элемент log означает, что t является достаточно длительным, чтобы увидеть бесконечный действующий радиальный поток. Взятие производной по функции суперпозиции времени (заданной правой частью уравнения (54 имеет преимущество включения в процедуру анализа предыдущих изме- 19008545 нений потока во времени и подтверждено практикой в анализе 15 испытания скважины. Чтобы вычислить параметры, используют нормированную функцию суперпозиции, заданную в виде Можно включать временные функции dp/dln(t), dp/dt0,25, dp/dt0,5 и т.д., используя простые методики. Для радиального потока (dp/dln(t цифровая производная давления (dp/dt) умножается на t. Для линейного потока (dp/dt0,5) имеем dp/dt2t и для билинейного потока (dp/dt0,25), dp/dt4t3/4. Точно так же сферическая производная становится dp/dt-2t3/2. Чтобы включить функцию суперпозиции времени в способ цифровой производной давления, используют цепное правило и вычисляют(dp/dt)/(dNSF/dt). Это может быть сделано либо численно, посредством вычисления функции суперпозиции времени как обычно и численного вычисления производной, либо посредством вычисления заранее функции (dNSF/dt), задаваемой в соответствии с уравнением Предлагается использовать последнее. Эта процедура также применяется для других временных преобразований, таких как псевдовременные функции, заданные согласно Agarwal и al.55, и эквивалентные понятию настройки. 3.4. Анализ чувствительности. Важными параметрами цифрового дифференцирующего устройства является его длина N, его полосовая частота fc отсечки и результирующая погрешностьаппроксимации (приближенная по отношению к идеальной производной). Взаимосвязи между этими тремя параметрами показаны параметрически ниже на фиг. 16 и 17. Погрешность в децибелах в зависимости от частоты отсечки, с N в качестве zпараметра показана на фиг. 16 для четного N и на фиг. 17 для нечетного N. В основном показано, что сопоставимые по длине дифференцирующие устройства с четным N являются всегда лучшими в том смысле, что максимальная погрешность аппроксимации меньше. Важным практическим соображением при выборе N (фиг. 20, 21) является неизбежная задержка N/2 в операции свертки, как задано уравнением (15). Необходимо ожидать N/2 выборок давления прежде,чем можно вычислять первую точку производной. Кроме того, в уравнении (15) имеется ограничение остановки вычисления производной в N/2 точках перед последней выборкой давления. Оптимальным выбором для N является, следовательно, наименьшее значение, для которого может быть получена приемлемая погрешность аппроксимации. Эмпирическая формула для прогнозирования N в терминах приемлемой погрешности дана в работе Herrmann и al.64 в виде и Чтобы продемонстрировать чувствительность характеристики производной к значению N, используется алгоритм Ремеза, чтобы генерировать коэффициенты для трех элементарных волновых сигналов с длинами N=10, 30 и 60. В алгоритме Ремеза была использована частота отсечки fc=0,1. На фиг. 22 представлены три элементарных волновых сигнала, на фиг. 23 проиллюстрированы частотные характеристики, вычисленные с использованием уравнения (12). Очевидно, что более длинный фильтр сформирует более точное идеальное дифференцирующее устройство, поскольку элементарный волновой сигналN=60 имеет самую сглаженную частотную характеристику от 0 до fc. Как ожидалось, абсолютное значение пропорционально частоте. Кроме того, более длинные элементарные сигналы имеют более сглаженное поведение, следуя частоте (f=0,15) полосы пропускания. Коэффициенты элементарных волновых сигналов для трех различных длин фильтра (фиг. 22). Частотные характеристики для трех коэффициентов элементарных волновых сигналов (фиг. 23). На фиг. 24 представлены характеристики производной, вычисленные с использованием элементарных волновых сигналов, описанных выше. Отклик давления в скважине по степени вскрытия, в бесконечном двухпористом резервуаре был вычислен с использованием уравнений (42) и (43). Сплошная линия представляет производную, вычисленную аналитически в области Лапласа, при этом имеется очень небольшое различие между вариантами для N=30 и N=60. Практически, это почти незначащее различие вряд ли оправдает использование фильтра длиной 60 (или более длинного) при заданной задержке N/2- 20008545 при вычислении точек производных. Характеристики СЦПД для трех различных длин фильтров (фиг. 24). Чувствительность частоты fc отсечки. Частота отсечки может быть такой, выше которой является доступным только сигнал нерезервуара (шумы). Из раздела 2.10 видно, что частота fc является независимой для всех практических целей рассматриваемой модели резервуара. Однако ожидается, что частота отсечки будет зависеть от качества измеренных данных. Например, если бы качество было низким, например, отношение сигнала к шуму равно единице, ожидалось бы, что fc должна быть низкой для того,чтобы фильтровать значительный вклад шумов. С другой стороны, для очень высоких отношений сигнала к шуму можно выбирать fc высокой, чтобы насколько возможно сохранить сигнал резервуара. Если известно отношение сигнала к шуму для измерения давления, можно найти оптимальное значение fc алгоритмически следующим образом: 1. Вычислить спектральную плотность мощности, как описано в разделе 2.10. 2. Интегрировать область под кривой СПМ от частоты 0 до частоты Найквиста. 3. Частота, на которой интегральная область равна отношению сигнала к шуму, является значением частоты отсечки. Это проиллюстрировано на фиг. 25 для отношения сигнала к шуму, равному единице. На относительной частоте 0,245 затененная область равна половине полной области под кривой. Другими словами,поскольку полный отклик (сигнал плюс шумы) представлен под кривой СПМ, и вклады сигнала и шумов являются равными (отношение сигнала к шуму - единица), частотой отсечки между сигналом и шумами является fc=0,245. Определение fc для единичного отношения сигнал-шум (фиг. 25). Чтобы проиллюстрировать чувствительность fc, используют пример скважины конечного радиуса по степени вскрытия для гомогенного резервуара двухпористого. Вычисляется безразмерный отклик давления и добавляется два процента случайного (белого) шума Сигнал и аналитическая производная представлены в виде диаграммы на фиг. 26 наряду с СЦПД,вычисленной при частоте fc отсечки, равной 0,10. Аналитическая производная была вычислена с использованием фактического значения без шумов, чтобы представлять идеальный отклик. СЦПД соответствует аналитической производной довольно хорошо, кроме области перехода от трещинного потока до полного потока системы. На фиг. 27 представлена СЦПД при fc=0,05. При этом СЦПД согласуется намного более близко с аналитической производной в целом, но имеет ошибку на фазе перехода. В заключение вычисляется СЦПД при fc=0,025. Результат, показанный на фиг. 28, согласуется очень хорошо с аналитической производной. Значение fc в этом диапазоне было ожидаемым, поскольку отношение сигнал-шум было довольно высоким. В заключение сравнивают результат обычного вычисления dp/dt, использующий центральную разность и 3 точки, с аналитической производной. Это сравнение показано на фиг. 29. Производная была вычислена, не используя сглаживания (L=0). Преимущество использования СЦПД является очевидным. Следует обратить внимание на важность использования одинакового алгоритма дифференцирования для измеренных данных и для аналитического решения при интерпретации данных переходного режима. Тогда как аналитическая производная может быть вычислена просто и эффективно с использованием теории преобразования Лапласа, согласованность между вычислениями измеренной и модельной производной является обязательной. 3.5. Примеры. Ниже показана эффективность СЦПД на двух примерных наборах данных. Первый пример на фиг. 30 представляет перепад давления для газовой скважины в Мексиканском заливе. Производная была вычислена, используя обычный способ центральных разностей по трем точкам, с нулевым сглаживанием. Параллельные, единичного наклона линии означают, что измеряемые давления изменяются в приращениях меньших, чем разрешающая способность измерителя давления. Чтобы лучше проиллюстрировать это поведение, диаграмма в логарифмическом масштабе показана на фиг. 31. При этом, поскольку также можно показывать отрицательные значения, измерение ниже разрешающей способности измерителя является более очевидным. Для каждой выборки фактическое значение давления является либо одним разрядом выше, либо одним разрядом ниже того, что измеритель может измерить. Статистически, если взято достаточное количество выборок, примерно половина измеренных значений будет слишком высокой,и половина будет слишком низкой. Это явление часто проходит незамеченным практически и, хуже, является часто причиной некорректных интерпретаций, например, можно ложно интерпретировать эти значения в качестве границы резервуара. Диаграмма в двойном логарифмическом масштабе дельта-давления и производной для примера 1(фиг. 30). Диаграмма в логарифмическом масштабе дельта-давления и производной для примера 1 (фиг. 31). Чтобы вычислить СЦПД для этого примера, сначала следует исследовать спектральную плотность- 21008545 мощности, представленную на фиг. 32. Более значительная часть энергии сигнала находится ниже частоты на 0,05 от частоты Найквиста, т.е. отношение сигнала к шуму является очень малым. При fc=0,05 и заданном по умолчанию значении 60 для длины фильтра, получают производную, показанную на фиг. 33. СЦПД, хотя и показывает некоторую неустойчивость в конце переходного режима, несомненно,лучше, чем обычный подход. Имеются также отрицательные значения в СЦПД, вследствие уменьшения изменения давления. Этот пример является хорошей иллюстрацией того, что мало что можно сделать,если исходное отношение сигнала к шуму является очень малым. Это часто имеет место в резервуарах с очень высокой проницаемостью или в ситуациях, когда был использован неточный измеритель. Спектральная плотность мощности для примера 1 показана на фиг. 32. СЦПД иллюстрируется для примера 1 на фиг. 33. Вторым примером является период нарастания, состоящий примерно из трехчасовых данных. Изменение давления и обычная производная давления показаны на фиг. 34. Производная была вычислена с использованием нулевого сглаживания. Вновь, видны параллельные, единичного наклона линии. Как в первом примере, это лучше иллюстрируется на диаграмме в логарифмическом масштабе на фиг. 35. В этом примере в отличие от предыдущего изменение давления увеличивается в течение полного переходного режима на поддающейся оценке скорости. Если не использовался измеритель с очень низкой разрешающей способностью, производная с шумами могла быть результатом других факторов,включая непосредственно процесс дифференцирования. При этом вычисляют СЦПД с использованием фильтра более короткой длины (N=40) и с большей частотой отсечки (fc=0,12). Это значение fc было получено при исследовании спектральной плотности мощности, показанной на фиг. 36. На нормированной частоте примерно 0,12 энергия сигнала давления уменьшается к тому значению, которое выступает в качестве минимального уровня шума (собственных шумов). Результирующая производная показана на фиг. 37. СЦПД в этом примере позволяет анализировать поведение резервуара и оценивать свойства резервуара на основании горизонтальной части производной. Спектральная плотность мощности для примера 2 показана на фиг. 36. СЦПД для примера 2 показана на фиг. 37. В приведенных примерах сравнивалась "сглаженная" производная СЦПД с обычной производной,не использующей сглаживание. Правомерным вопросом в этом пункте является, какое значение сглаживания L требует обычный способ, использующий центральную разность и три точки, чтобы сформировать кривые производной с таким же качеством, как СЦПД. Ответ зависит и от частоты дискретизации, и частотного спектра измеренного давления. Сравнение СЦПД с обычной производной L=0,09 показано на фиг. 38. При интерпретации данных с шумами с использованием обычных способов используют максимальную величину сглаживания, например Lmax без изменения фактического сигнала резервуара. Традиционно это осуществлялось вслепую, значение Lmax было неизвестно. Согласно изобретению становится возможным определять количество Lmax посредством выполнения сравнений центрально-разностных производных с СЦПД, вычисленных с использованием частоты отсечки между сигналом резервуара и сигналом нерезервуара. На фиг. 38 представлен СЦПД (как вычислено выше) центрально-разностной производной с использованием трех точек и параметра L сглаживания, соответствующего 0,09. Две кривые производных перекрывают друг друга очень близко, что означает, что это максимальное значение L,которое может быть использовано без изменения самого сигнала резервуара. Это является главным отличительным признаком изобретения, т.е. теперь можно определить значение прежде субъективного выбора оптимального значения сглаживания Lmax. Чтобы проиллюстрировать опасность "пересглаживания",на фиг. 39 показан результат для нескольких различных значений L. 3.6. Программная реализация. Способы, описанные в предыдущих разделах, были осуществлены на языке ФОРТРАН (FORTRAN) и включены в приложение для Microsoft Windows. Это приложение использовалось, чтобы вычислить примеры, приведенные в предыдущем разделе. Алгоритмы вычисления спектральной плотности мощности и дискретной свертки выполнены в виде динамически подсоединяемых библиотек (DLL). Преимущество этого состоит в том, что пользовательский интерфейс остается независимым, давая возможность переноса между различными операционными системами (например, Windows, Windows NT, AIX,Unix). Интерфейс с пользовательским приложением показан ниже. Факультативная возможность СЦПД может просто быть добавлена к любым имеющимся способам производной в программном обеспечении анализа испытания скважины (т.е. способам конечных разностей с двумя точками, с тремя точками, правых, центральных и левых). Входными данными для вычисления, как указано выше, являются длина N фильтра, и частота fc отсечки. Длина фильтра может быть либо введена пользователем, либо вычислена с использованием эмпирических формул, заданных в соответствии с уравнением (57). Значение fc может быть вручную введено или графически выбрано из диаграммы кривой спектральной плотности мощности. Для ситуаций, в которых идеальное значение fc не является очевидным, является доступным режим чувствительности. При этом пользователь может вводить до пяти значений fc, и СЦПД будет вычислен для каждого из значений. Идеальное значение может быть определено затем визуально. Эта возможность- 22008545 также полезна для сравнения СЦПД с обычными сглаженными производными, как указано выше в разделе 3.5. Дополнительный подход для определения оптимального значения частоты отсечки также был реализован программно, но в данный момент остается экспериментальным. Ожидается, что этот подход ограничит и минимальное, и максимальное значение fc на основании полученного знания теории кривых восстановления давления. Методика использует неявное, но мощное понятие обработки сигналов, известное как неравенство 59 Бернштайна. Это малоизвестное отношение может быть сформулировано следующим образом. Если сигнал p(t) имеет верхнюю границу М, по его абсолютной величине на рассматриваемом временном интервале, т.е. если и если сигнал также ограничен по полосе частот до , т.е. если р=0 для , то ограниченный по абсолютному значению сигнал производной задается согласно Следует обратить внимание, что если можно оценивать максимальные значения p'(t) и p(t), то можно решить уравнения (63) и (64) для . Этот предел полосы частот может использоваться, чтобы определить более низкую границу частоты дискретизации измерителя давления в секунду, т.е. fsam/ и границы частоты отсечки, т.е. fsamfc/2. Например, на основании нарастания давления в переходном режиме экстраполированное давление р обеспечивает границу максимального абсолютного давления. Следовательно Теперь необходимо определить максимально возможное значение производной давления р'(t). При этом р'(t) является производной по времени: либо по t, либо по t. Ожидается, что максимум производной должен произойти рано в переходном режиме, когда градиенты давления внутри и непосредственно рядом со скважиной имеют свои самые высокие значения. Т.е. ожидается, что оценки резервуара скважины и верхнего слоя должны быть принципиальными параметрами при оценке максимальной производной давления. Это совместимо с процессом диффузии, т.е. что частота изменения давления уменьшается монотонно. Можно использовать оценки этих определяющих параметров, чтобы, в свою очередь,оценивать максимальное значение р'(t). В качестве альтернативы, можно просто вычислять производную один раз с использованием обычного способа центральной разности по трем точкам (или любого другого способа), чтобы достичь приближенного максимального значения для входных данных уравнения (65). В программной реализации данный способ осуществлен итерационно, при каждой итерации вычисляют СЦПД, используя текущую оценку fc. Максимальное значение СЦПД используется в качестве входных данных, чтобы вычислять следующее значение fc и следующую СЦПД. Вычисление, требуемое для вычисления СЦПД, примерно эквивалентно традиционным конечноразностным способам; вычисление спектральной плотности мощности и автоматическое определение fc являются только немного более дорогостоящими. Суть данного раздела состоит в том, чтобы обратить внимание, что СЦПД может быть легко реализован в имеющемся программном обеспечении испытания скважины. На фиг. 40 иллюстрируется окно ввода параметров СЦПД. 4. Выводы. В данном описании был представлен новый способ вычисления производной для динамических данных неустановившегося давления. Способ объединяет несколько фундаментальных понятий из литературы по обработке сигналов с полученным знанием системы измерения, чтобы разделить собранные данные испытания скважины на поведение резервуара и нерезервуара. Результатом является более надежная кривая производной, которая дает аналитику более высокую степень достоверности при диагностировании поведения резервуара и идентификации режимов потока для оценки параметров. Предоставленные примеры продемонстрировали эффективность нового способа. Кроме того, СЦПД имеет следующие преимущества: СЦПД обеспечивает физическое ощущение (понимание) степени сглаживания производной; в отличие от субъективного подхода, используемого в настоящее время в традиционных алгоритмах производных; СЦПД поддается автоматическому согласованию прототипа кривой, в частности способов, основанных на распознавании образов, вследствие уменьшенного разброса точек производных; СЦПД может использоваться либо в реальном масштабе времени, по мере сбора данных, либо в микропрограммном обеспечении регистрирующих измерителей. В последнем случае, СЦПД может оптимизировать длительность каждого переходного процесса на основании программируемого минимального отношения сигнал-шум; дополнительные методики цифровой обработки сигналов, такие как избыточная дискретизация, могут использоваться, чтобы дополнительно улучшить значимость производной давления с использовани- 23008545 ем СЦПД; способы анализа переходных процессов, которые используют производные более высокого порядка, были разработаны, но редко использовались вследствие недостаточной устойчивости в заключительной производной. Пример дан в работе Cinco-Ley, et al.57, в которой применяют вторую производную давления 2p/t2, чтобы определить свойства резервуара, используя подход мгновенного источника. Другие попытки были осуществлены, чтобы использовать производные более высокого порядка для содействия распознаванию различных режимов 58 потоков; рассматривая данные кривых восстановления давления в частотной области и зная физические пределы частотной характеристики резервуара, можно устанавливать пределы, по которым точки данных могут рассматриваться откликом резервуара и теми, которые могут рассматриваться шумом. Эти пределы могут быть представлены на диаграмме в двойном логарифмическом масштабе в качестве доверительных интервалов, чтобы содействовать идентификации режимов потока и улучшить процесс оценки параметров, используя и прямые способы, и автоматические способы согласования прототипа кривой. Размерности параметров, упомянутых в описанииCD - безразмерный коэффициент хранилища скважины,fc - частота отсечки, радиан/секунду или Гц,fmax - максимальная частота, радиан/секунду или Гц,fN - частота Найквиста, радиан/секунду или Гц,f(s) - функция двухпористости,H(z) - цифровая передаточная функция,h(m) - коэффициент элементарного волнового сигнала,I0 - модифицированная функция Бесселя (Bessel) первого рода, нулевой порядок,I1 - модифицированная функция Бесселя первого рода, первый порядок,IN - оценка периодограммы,j - мнимое число, -1,K0 - модифицированная функция Бесселя третьего рода, нулевой порядок,K1 - модифицированная функция Бесселя третьего рода, первый порядок,L - интервал дифференцирования и число экстремальных частот,N - длина фильтра,NSF - нормированная функция суперпозиции,р - давление, фунт на кв.дюйм (PSI),pD - безразмерное давление,pWf - забойное гидродинамическое скважинное давление, фунт на кв.дюйм,q - забойная скорость потока, баррель/день или (m3/день),rе - внешний радиус, футы (м),reD - безразмерный радиус, re/rw,rw - радиус скважины, футы (м),RX - функция автокорреляции ,s - переменная Лапласа,S - поверхность (общая),SF - функция суперпозиции,t - временной интервал, секунды,u - модифицированная переменная Лапласа,z - комплексная переменная, - погрешность,(n) - одиночная выборка, - коэффициент потока межпористости, - частотная переменная или отношение упругоемкости. Ссылки 1. Ozkan, E. and Raghavan, R. "New Solutions for Well-Test Analysis Problems", Part I, "Analytical Considerations", SPEFE (Sept. 1991) 359-38. 2. Ozkan, E. and Raghavan, R. "New Solutions for Well-Test Analysis Problems", Part II, "AnalyticalCIMMS, Friday October 4, 2002. Будет очевидно, что это же, соответственно описываемое изобретение, может быть изменено многими способами. Такие изменения не должны рассматриваться в качестве выхода за рамки существа и объема изобретения. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ генерирования выходного сигнала, не содержащего шумов, в ответ на входной сигнал с шумами, являющийся сигналом измерения, заключающийся в том, что осуществляют свертку входного сигнала, содержащего шумы, с элементарным волновым сигналом, генерируют выходной сигнал в ответ на этап свертки, не содержащий шумов. 2. Способ по п.1, отличающийся тем, что входной сигнал является функцией, представляющей сигнал измерения давления в скважине, который содержит шумы. 3. Способ по п.1, отличающийся тем, что выходной сигнал является производной входного сигнала,причем выходной сигнал не содержит шумов. 4. Способ по п.3, отличающийся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом осуществляют свертку входного сигнала с элементарным волновым сигналом с использованием уравнения 5. Способ по п.4, отличающийся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала. 6. Способ по п.5, отличающийся тем, что производную элементарного волнового сигнала формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. 7. Способ по п.3, отличающийся тем, что на этапе свертки входного сигнала с элементарным волно- 26008545 вым сигналом осуществляют свертку входного сигнала с элементарным волновым сигналом с использованием уравнения 8. Способ по п.7, отличающийся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала. 9. Способ по п.8, отличающийся тем, что производную элементарного волнового сигнала формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. 10. Способ по п.1, отличающийся тем, что дополнительно осуществляют свертку выходного сигнала с элементарным волновым сигналом, генерируют дополнительный выходной сигнал в ответ на этап дополнительной свертки, при этом дополнительный выходной сигнал не содержит шумов. 11. Способ по п.10, отличающийся тем, что выходной сигнал является первой производной входного сигнала, причем выходной сигнал не содержит шумов. 12. Способ по п.11, отличающийся тем, что дополнительный выходной сигнал является второй производной входного сигнала, причем дополнительный выходной сигнал не содержит шумов. 13. Способ по п.12, отличающийся тем, что на этапе осуществления свертки входного сигнала с элементарным волновым сигналом и на этапе дополнительной свертки выходного сигнала с элементарным волновым сигналом используют уравнение 14. Способ по п.13, отличающийся тем, что элементарный волновой сигнал формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. 15. Способ по п.12, отличающийся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом и этапе дополнительной свертки выходного сигнала с элементарным волновым сигналом используют уравнение 16. Способ по п.15, отличающийся тем, что элементарный волновой сигнал формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. 17. Способ по п.1, отличающийся тем, что входной сигнал является частной функцией, содержащей набор из выборок цифровых данных, представляющих сигналы измерения давления в скважине, которые включают в себя шумы. 18. Способ по п.17, отличающийся тем, что выходной сигнал является производной частной функции, причем производная частной функции не содержит шумов. 19. Способ по п.18, отличающийся тем, что на этапе свертки цифрового входного сигнала с элементарным волновым сигналом осуществляют свертку входного сигнала с элементарным волновым сигналом с использованием уравнения 20. Способ по п.19, отличающийся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала. 21. Способ по п.20, отличающийся тем, что производную элементарного волнового сигнала формируют из ограниченного по полосе частот преобразованного сигнала идеального дифференцирующего устройства, при этом преобразованный сигнал с ограниченной полосой частот имеет расчетное значение частоты отсечки ограниченной полосы частот. 22. Способ по п.21, отличающийся тем, что расчетное значение частоты отсечки ограниченной полосы частот выбирают в качестве значения, выше которого шумы являются основной составляющей полного сигнала. 23. Способ по п.20, отличающийся тем, что вычисляют один или несколько коэффициентов элементарного волнового сигнала с использованием способа Чебышева, используя алгоритм замен Ремеза. 24. Устройство хранения программы, считываемой машиной, содержащей программу из команд,выполняемых машиной, для осуществления этапов способа генерирования выходного сигнала, не содержащего шумов, в ответ на входной сигнал, являющийся сигналом измерения, который содержит шумы, в указанном способе осуществляют свертку входного сигнала, содержащего шумы, с элементарным волновым сигналом, генерируют выходной сигнал в ответ на этап свертки, не содержащий шумов. 25. Устройство по п.24, отличающееся тем, что упомянутый входной сигнал является функцией,представляющей сигнал измерения давления в скважине, который содержит шумы. 26. Устройство по п.24, отличающееся тем, что выходной сигнал является производной входного сигнала, причем выходной сигнал не содержит шумов.- 27008545 27. Устройство по п.26, отличающееся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом используется уравнение 28. Устройство по п.27, отличающееся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала. 29. Устройство по п.28, отличающееся тем, что производную элементарного волнового сигнала формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. 30. Устройство по п.26, отличающееся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом используется уравнение 31. Устройство по п.30, отличающееся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала. 32. Устройство по п.31, отличающееся тем, что производную элементарного волнового сигнала формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. 33. Устройство по п.24, отличающееся тем, что дополнительно осуществляют свертку выходного сигнала с элементарным волновым сигналом, генерируют дополнительный выходной сигнал в ответ на этап дополнительной свертки, причем дополнительный выходной сигнал не содержит шумов. 34. Устройство по п.33, отличающееся тем, что выходной сигнал является первой производной входного сигнала, причем выходной сигнал не содержит шумов. 35. Устройство по п.34, отличающееся тем, что дополнительный выходной сигнал является второй производной входного сигнала, при этом дополнительный выходной сигнал не содержит шумов. 36. Устройство по п.35, отличающееся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом и на этапе дополнительной свертки выходного сигнала с элементарным волновым сигналом используют уравнение 37. Устройство по п.36, отличающееся тем, что элементарный волновой сигнал формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. 38. Устройство по п.35, отличающееся тем, что на этапе свертки входного сигнала с элементарным волновым сигналом и на этапе дополнительной свертки выходного сигнала с элементарным волновым сигналом используют уравнение 39. Устройство по п.38, отличающееся тем, что элементарный волновой сигнал формируют из одиночной выборки ответного сигнала ограниченного по полосе частот оптимального линейного фазового цифрового дифференцирующего устройства с конечной импульсной характеристикой. 40. Устройство по п.24, отличающееся тем, что упомянутый входной сигнал является частной функцией, содержащей набор из выборок цифровых данных, представляющих сигналы измерения давления в скважине, которое включает в себя шумы. 41. Устройство по п.40, отличающееся тем, что выходной сигнал является производной частной функции, причем производная частной функции не содержит шумов. 42. Устройство по п.41, отличающееся тем, что на этапе свертки цифрового входного сигнала с элементарным волновым сигналом осуществляется свертка входного сигнала с элементарным волновым сигналом с использованием уравнения 43. Устройство по п.42, отличающееся тем, что элементарный волновой сигнал является производной элементарного волнового сигнала. 44. Устройство по п.43, отличающееся тем, что производная элементарного сигнала формируется из ограниченного по полосе частот преобразованного сигнала идеального дифференцирующего устройства,при этом преобразованный сигнал с ограниченной полосой частот имеет расчетное значение частоты отсечки ограниченной полосы частот. 45. Устройство по п.44, отличающееся тем, что расчетное значение частоты отсечки ограниченной полосы частот выбрано в качестве значения, выше которого шумы являются основной составляющей полного сигнала.- 28008545 46. Устройство по п.43, отличающееся тем, что один или несколько коэффициентов элементарного волнового сигнала вычисляется с использованием способа Чебышева, используя алгоритм замен Ремеза. 47. Способ генерирования выходного сигнала, не содержащего шумов, в ответ на входной сигнал с шумами, являющийся сигналом измерения, заключающийся в том, что осуществляют свертку входного сигнала, содержащего шумы, с элементарным волновым сигналом, генерируют выходной сигнал в ответ на этап свертки, при этом выходной сигнал представляет производную входного сигнала и не содержит шумов. 48. Устройство хранения программы, считываемой машиной, содержащей программу из команд,выполняемых машиной, для осуществления этапов способа генерирования выходного сигнала, не содержащего шумов, в ответ на входной сигнал с шумами, являющийся сигналом измерения, заключающийся в том, что осуществляют свертку входного сигнала, включающего в себя шумы, с элементарным волновым сигналом, генерируют выходной сигнал в ответ на этап свертки, причем выходной сигнал представляет производную входного сигнала и не содержит шумов.
МПК / Метки
МПК: G06F 17/10, E21B 47/06, G01V 1/36
Метки: программы, способ, давления, хранения, производной, устройство, цифровой
Код ссылки
<a href="https://eas.patents.su/30-8545-sposob-i-ustrojjstvo-hraneniya-programmy-dlya-cifrovojj-proizvodnojj-davleniya.html" rel="bookmark" title="База патентов Евразийского Союза">Способ и устройство хранения программы для цифровой производной давления</a>
Способ и устройство получения и хранения личного цифрового сертификата и способ защищенного обмена цифровой информацией
Номер патента: 8186
Опубликовано: 27.04.2007
Авторы: Щербаков Андрей Юрьевич, Домашев Алексей Владимирович, Сотский Сергей Вячеславович, Дуйков Евгений Александрович
МПК: H04L 9/16, G06Q 30/00, H04L 9/30...
Метки: цифрового, получения, информацией, личного, защищенного, устройство, цифровой, сертификата, обмена, способ, хранения
Формула / Реферат:
1. Способ получения и хранения личного цифрового сертификата, заключающийся в том, что цифровой сертификат, содержащий электронную цифровую подпись, от уполномоченного органа передают в запоминающее устройство для долговременного хранения; личный закрытый ключ из генератора случайных чисел передают в запоминающее устройство для долговременного хранения; личный закрытый ключ, хранимый в запоминающем устройстве для долговременного хранения,...
Способ и устройство передачи цифровой информации
Номер патента: 8528
Опубликовано: 29.06.2007
Авторы: Дуйков Евгений Александрович, Сотский Сергей Вячеславович, Домашев Алексей Владимирович, Щербаков Андрей Юрьевич
МПК: G02F 2/00, G02F 1/00, H04B 10/10...
Метки: способ, информации, устройство, цифровой, передачи
Формула / Реферат:
1. Способ передачи цифровой информации, предусматривающий: (а) модуляцию потока электромагнитных волн, заключающуюся в том, что от источника электромагнитных волн создают поток электромагнитных волн, по меньшей мере часть которого направляют на прозрачную в диапазоне упомянутых электромагнитных волн матрицу-передатчик, способную изменять по меньшей мере на части своей поверхности свои свойства проницаемости в зависимости от содержания подаваемой...
Способ и устройство для цифровой обработки текстильного материала
Номер патента: 8332
Опубликовано: 27.04.2007
Автор: Краамер Йоханнес Антониус
МПК: B41J 11/00, D06B 11/00
Метки: материала, обработки, способ, цифровой, текстильного, устройство
Формула / Реферат:
1. Способ цифровой обработки субстрата, в частности текстильного изделия, при использовании обрабатывающего устройства, содержащего несколько сопел для нанесения одного или более веществ на текстильный материал, и конвейер для транспортировки текстильного материала мимо сопел, при этом сопла расположены по порядку в несколько последовательно размещенных рядов, продолжающихся поперечно направлению транспортировки текстильного изделия,...
Датчик давления и способ изготовления датчика давления
Номер патента: 4582
Опубликовано: 24.06.2004
Авторы: Хегнер Франк, Флегель Карл, Росскопф Бернд, Банхольцер Карл-Хайнц
МПК: G01L 9/00
Метки: способ, датчик, давления, датчика, изготовления
Формула / Реферат:
1. Датчик давления, содержащий основание (1, 23, 25), соединенную с основанием (1, 23, 25), образуя измерительную камеру (3, 29, 31), мембрану (5, 27), которая при работе испытывает зависимое от измеряемого давления (p, p1-p2) отклонение, образованную обращенной к мембране стороной основания (1, 23, 25) постель мембраны, на которую нанесен по меньшей мере один электрод (7, 33, 67), который вместе с нанесенным на мембрану (5, 27) ответным...
Способ и устройство для повторного разгона транспортного средства, оборудованного воздушными компрессорами высокого давления.
Номер патента: 834
Опубликовано: 24.04.2000
Авторы: Негр Сирил, Негр Ги
МПК: F02B 75/10, B60T 1/10
Метки: устройство, воздушными, средства, высокого, компрессорами, оборудованного, разгона, способ, транспортного, повторного, давления
Формула / Реферат:
1. Способ повторного разгона транспортного средства, оборудованного двигателем, не выделяющим вредные выбросы, или двигателем с контролируемыми вредными выбросами, содержащим отдельную камеру сгорания (2), в которую вводят при работе с воздухом определенное количество добавочного сжатого и не образующего вредных выбросов газа, поступающего из главной внешней емкости (23), в которой этот сжатый газ находится под высоким давлением и по существу...
Предыдущий патент: Игровой автомат и игровая система
Следующий патент: Вкладыш доильного стакана и доильный стакан
Случайный патент: Ингибирующие mtp арилпиперидины или пиперазины, замещенные 5-членными гетероциклами