Устройство, способ и система для улучшения моделирования коллектора с использованием мультипликативной предварительной обработки шварца с наложением для адаптивных неявных линейных систем
Формула / Реферат
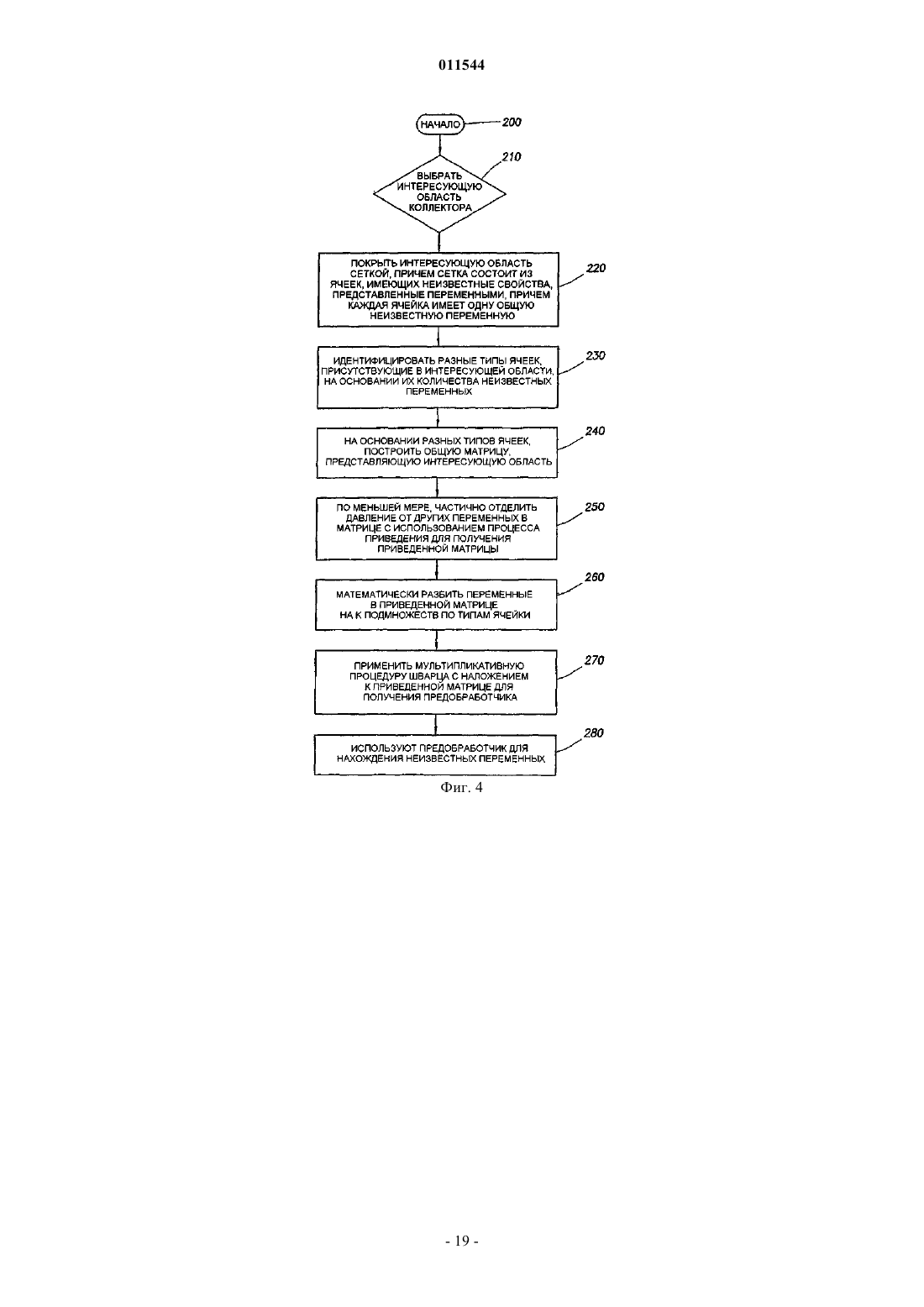
1. Способ осуществления моделирования коллектора, содержащий этапы, на которых:
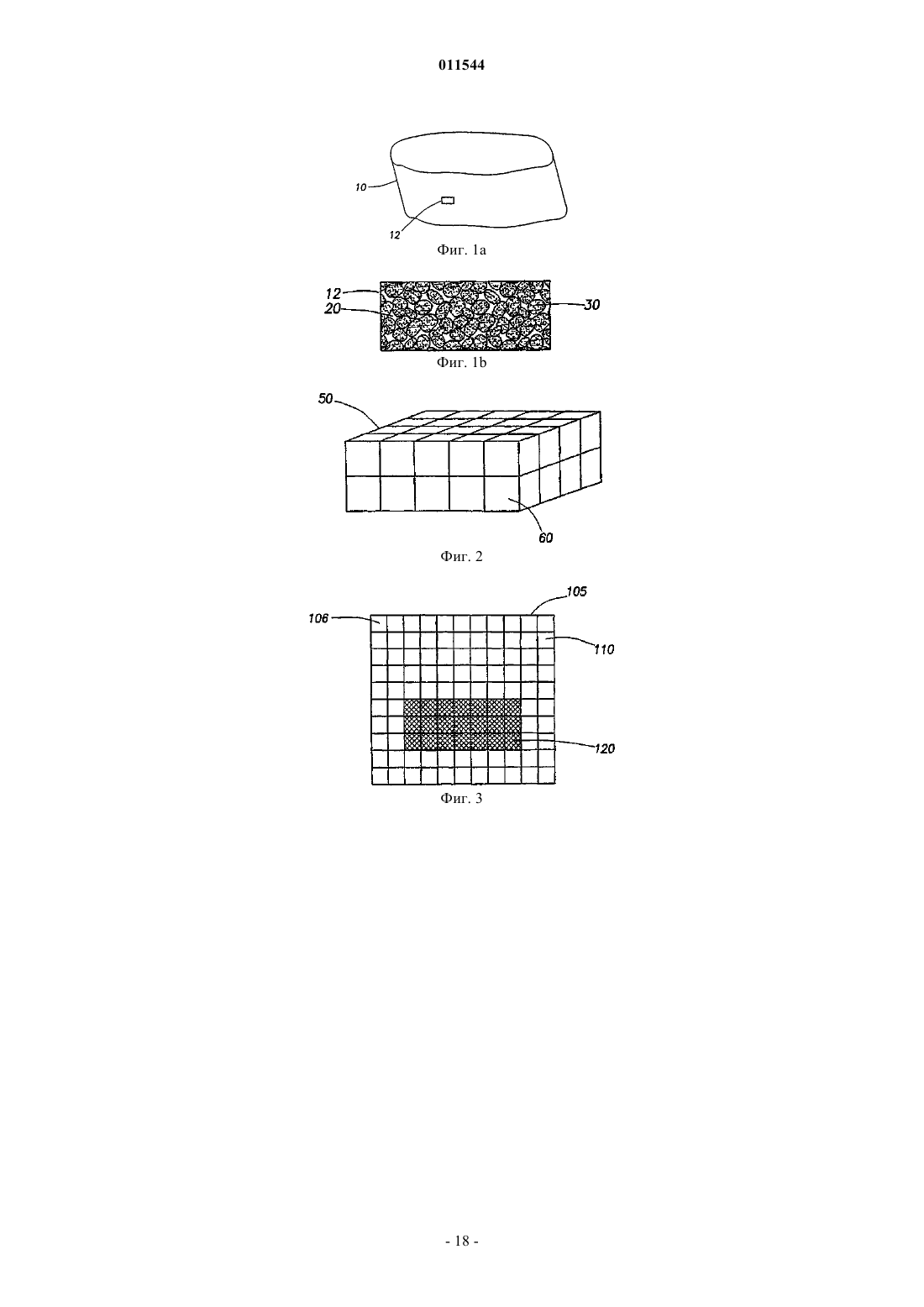
a) строят модель коллектора интересующей области путем наложения сетки на интересующую область, причем сетка содержит один или несколько типов ячеек, причем типы ячеек различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной,
b) идентифицируют разные типы ячеек для сетки,
c) строят общую матрицу для модели коллектора на основании разных типов ячеек,
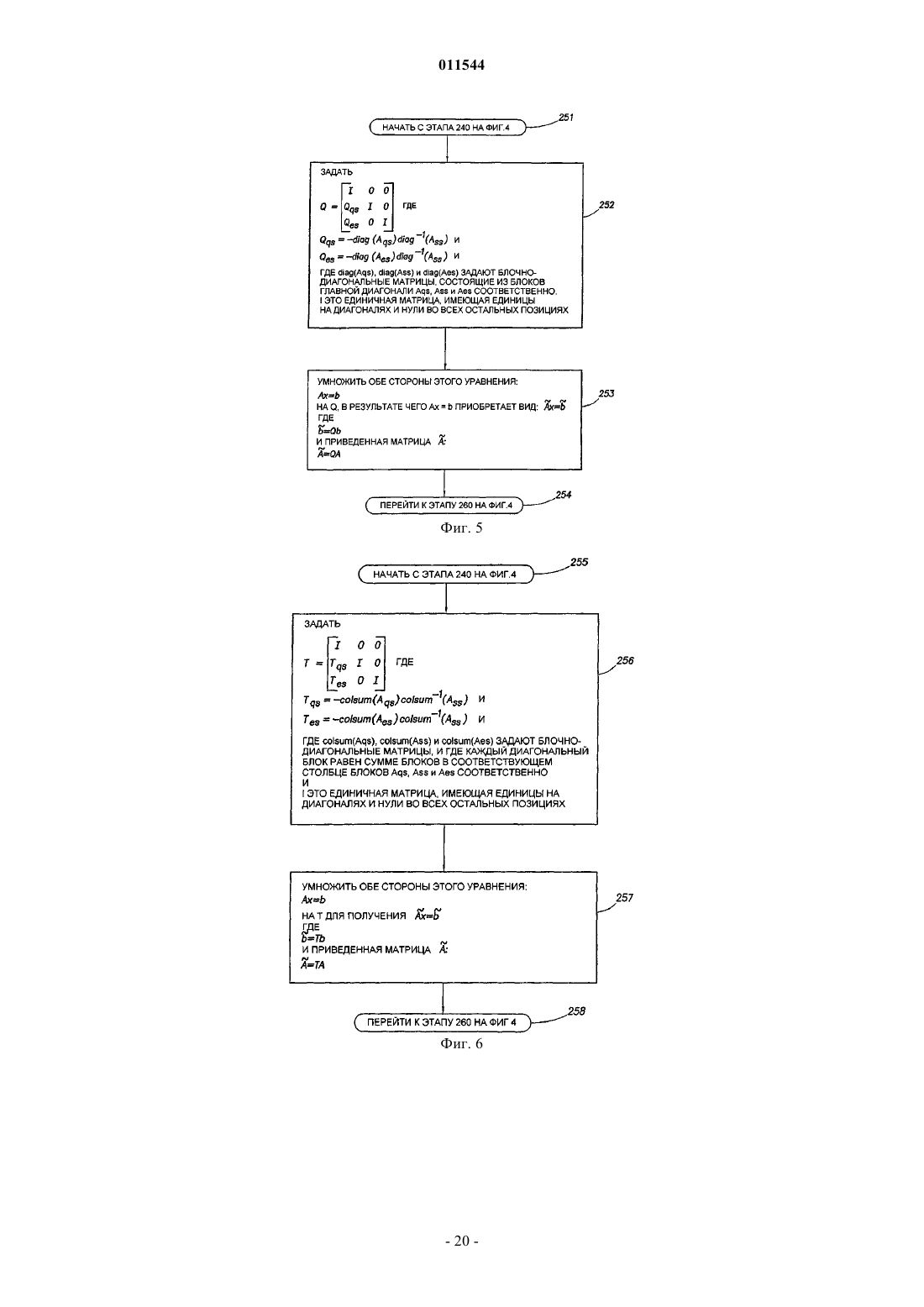
d) по меньшей мере, частично отделяют общую переменную от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,
e) математически разбивают переменные в приведенной матрице на k подмножеств по типам ячейки, и
f) применяют мультипликативную процедуру Шварца с наложением к приведенной матрице для получения предобработчика,
g) находят неизвестные переменные с использованием предобработчика, полученного на этапе (f), и
h) повышают выход флюида в интересующей области с использованием моделирования коллектора.
2. Способ по п.1, в котором на этапе построения (b) получают структурированные сетки.
3. Способ по п.1, в котором на этапе построения (b) получают неструктурированные сетки.
4. Способ по п.1, в котором общей переменной является давление.
5. Способ по п.1, в котором общей переменной является температура.
6. Способ по п.1, в котором общую матрицу, построенную на этапе построения (с), записывают в блочном виде, на основании количества типов ячеек в интересующей области.
7. Способ по п.6, в котором существует тип ячейки с одной переменной и общей матрице [[А]] требуется одна строка блоков и один столбец блоков.
8. Способ по п.6, в котором для каждой ячейки с одной переменной, общей матрице [[А]] требуется одна строка блоков и один столбец блоков и для каждой ячейки с множественными переменными с одним столбцом блоков общей матрице [[А]] требуется две дополнительных строки блоков и два дополнительных столбца блоков.
9. Способ по п.1, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием квази-IMPES приведения.
10. Способ по п.1, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием истинного IMPES приведения.
11. Способ по п.1, в котором на этапе (е) математического разбиения переменных в приведенной матрице дополнительно:
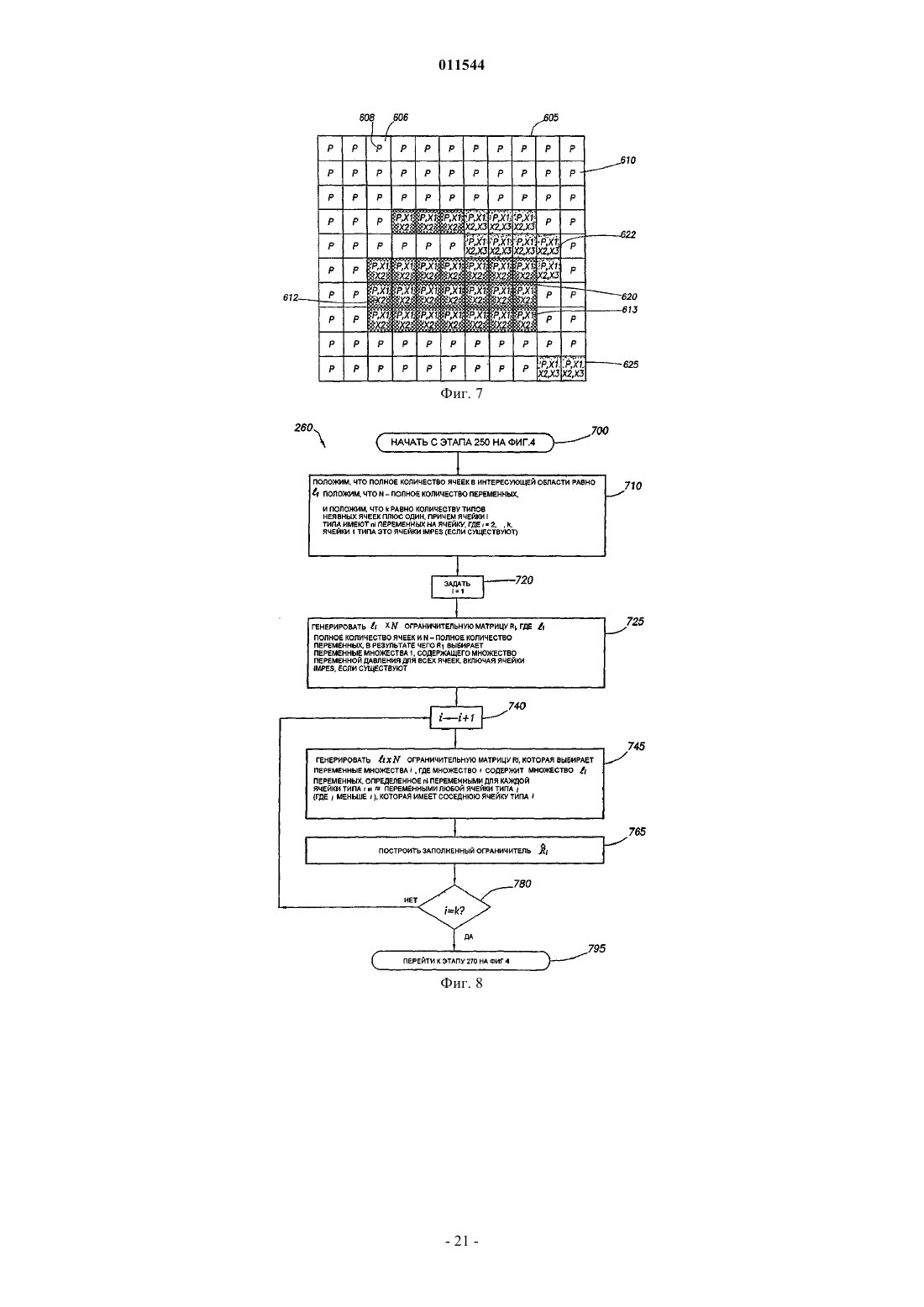
(е)(1) задают полное количество ячеек в интересующей области равным li, задают N равным полному количеству переменных, задают k равным количеству типов неявных ячеек плюс один, причем ячейки i типа имеют ni переменных на ячейку, где i = 1, 2, ..., k, причем ячейки 1 типа являются ячейками IMPES, если существуют,
(е)(2) задают i равным единице,
(е)(3) генерируют li_N ограничительную матрицу Ri, где li - полное количество ячеек и N - полное количество переменных, в результате чего R1 выбирает переменные Множества 1,
(е)(4) задают i равным i плюс один,
(е)(5) генерируют li_N ограничительную матрицу Ri, которая выбирает переменные Множества i,
(е)(6) определяют заполненный ограничитель,
(е)(7) если i не равно k, повторяют этапы (е)(4)-(е)(6), пока i не станет равным k.
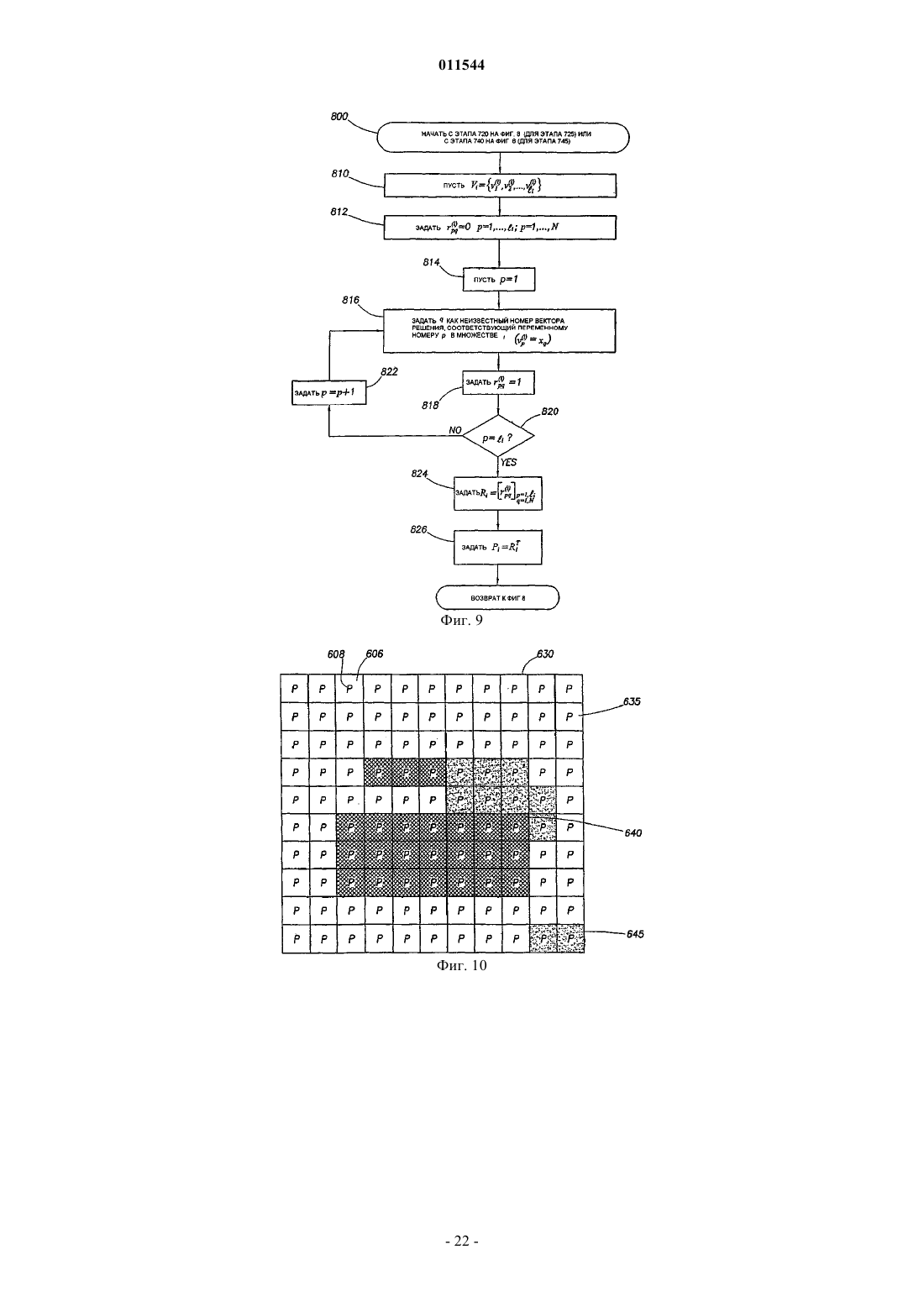
12. Способ по п.11, в котором на этапе (е)(6) определения заполненного ограничителя дополнительно
(е)(6)(i) задают ![]()
(е)(6) (ii) задают rpq(i) равным нулю, p в диапазоне значений 1, ..., li; и q в диапазоне значений 1, ..., N,
(е)(6) (iii) задают p равным 1,
(е)(6) (iv) задают q как неизвестный номер вектора решения, соответствующий переменному номеру р в Множестве i (vp(i)=xq),
(е)(6) (v) задают rpq(i) равным единице,
(е)(6) (vi) определяют, равно ли p величине li, и если нет, задают р равным p + 1 и возвращаются к этапу (е)(6)(iv), а если p равно li, задают Ri равной
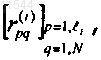
и
(е)(6) (vii) задают Pi равной RiT.
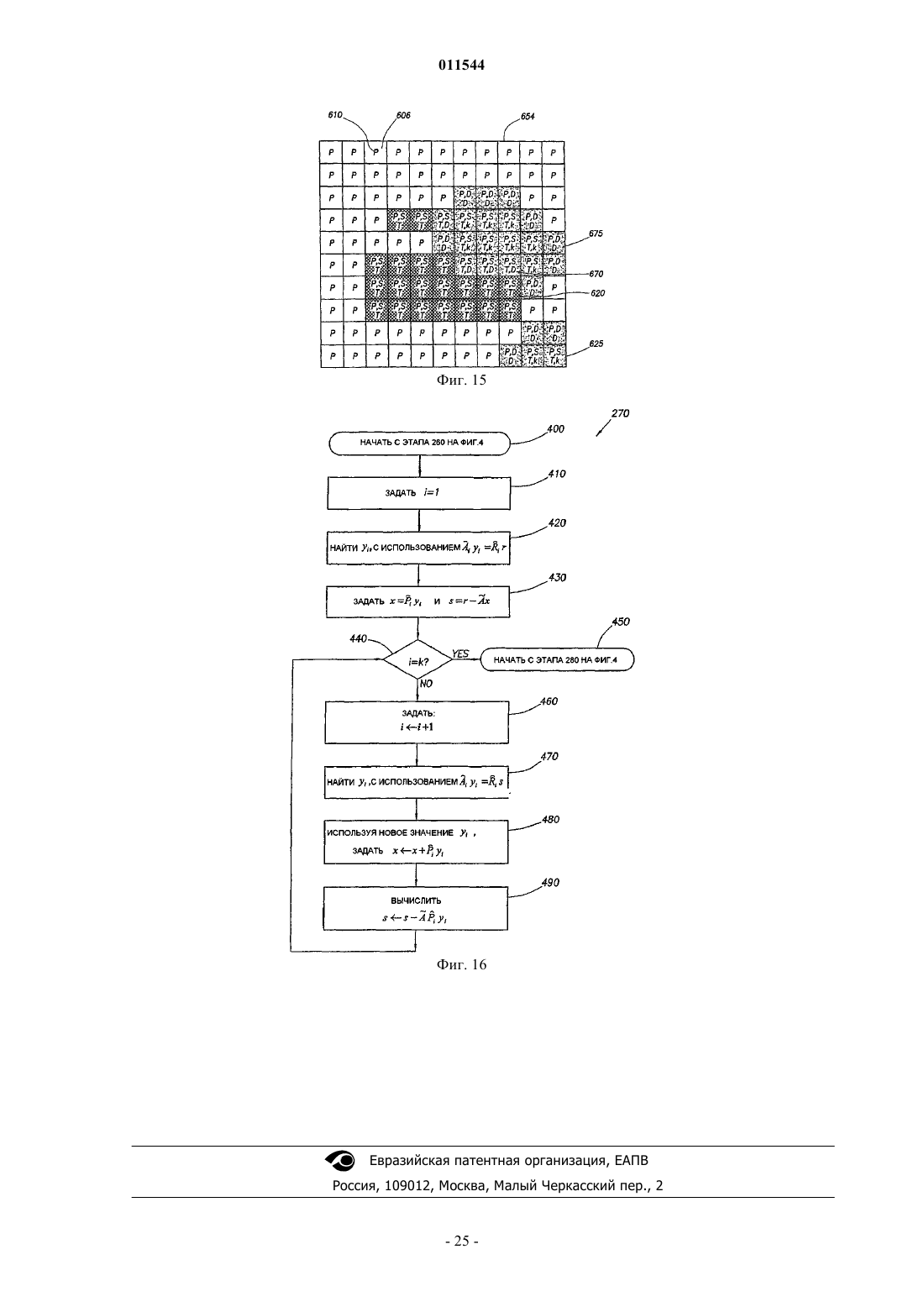
13. Способ по п.1, где на этапе (f) применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно:
(f)(1) задают i равным единице,
(f)(2) находят давления y во всех ячейках, с использованием уравнения ![]()
(f)(3) задают приближенное решение x равным ![]() и задают s равным
и задают s равным ![]()
(f)(4) определяют, равно ли i величине k, и если нет,
(f)(4) (i) задают i равным i плюс 1,
(f)(4) (ii) находят yi с использованием ![]()
(f)(4) (iii) используя новое значение yi, вычисляют новое значение x, равное x плюс ![]()
(f)(4) (iv) вычисляют новое значение s, равное s минус произведение ![]() и
и
(f)(4) (v) возвращаются к этапу определения (f) (4), пока i не станет равным k.
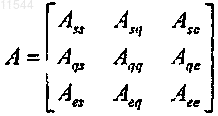
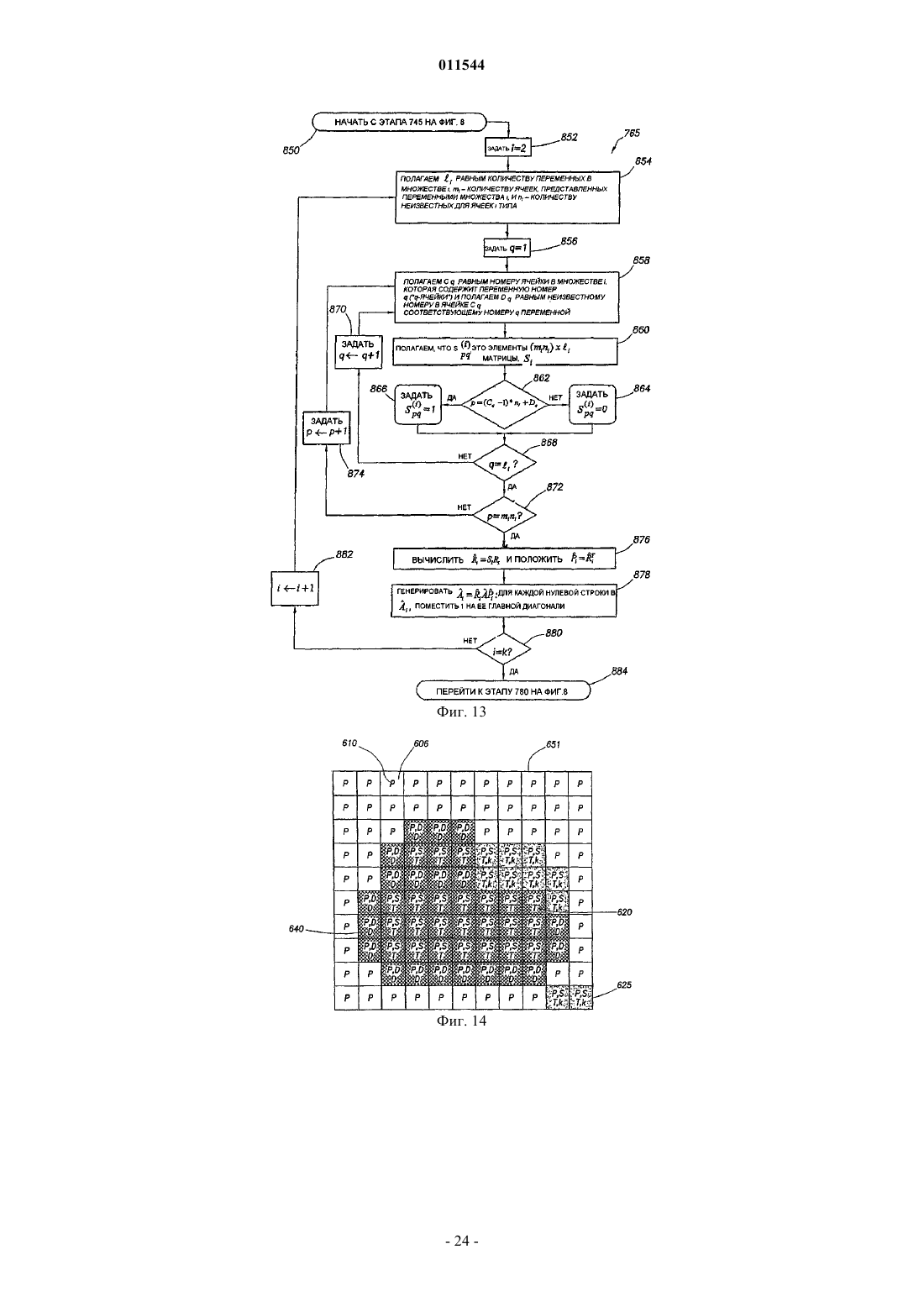
14. Способ по п.1, в котором существует k-1 разных типов ячеек с m>1 и на этапе (е) математического разбиения переменных в приведенной матрице дополнительно:
(е)(1) для каждой ячейки типа mi>1, i=1 ... k-1 формируют подсистему, содержащую ячейки типа mi и их соседи другого типа, причем каждая подсистема имеет постоянный размер блока,
(е)(2) для соседей типа n>mi выбирают m общих переменных при построении подсистем, и
(е) (3) для n<m, выбирают все n переменных и заполняют систему m-n фиктивными переменными.
15. Способ по п.1, в котором общей переменной является давление, и в котором общую матрицу, построенную на этапе построения (с), записывают в блочном виде, на основании количества типов ячеек в интересующей области.
16. Способ по п.15, в котором для каждой ячейки с одной переменной, общей матрице [[А]] требуется одна строка блоков и один столбец блоков, и для каждой ячейки с множественными переменными с одним столбцом блоков общей матрице [[А]] требуется две дополнительных строки блоков и два дополнительных столбца блоков.
17. Способ по п.16, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием истинного IMPES приведения.
18. Способ по п.16, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием квази-IMPES приведения.
19. Способ осуществления моделирования коллектора, с использованием модели коллектора интересующей области, причем на интересующую область наложена сетка, причем сетка интересующей области содержит один или несколько типов ячеек, причем типы ячеек различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной, содержащий этапы, на которых:
a) идентифицируют разные типы ячеек для сетки,
b) строят общую матрицу для модели коллектора на основании разных типов ячеек,
c) по меньшей мере, частично отделяют общую переменную от других неизвестных переменных в матрицх ё использованием процесса приведения для получения приведенной матрицы,
d) математически разбивают переменные в приведенной матрице на k подмножеств по типам ячейки, при этом дополнительно:
(d)(1) задают полное количество ячеек в интересующей области равным li, задают N равным полному количеству переменных, задают k равным количеству типов неявных ячеек плюс один, причем ячейки i типа имеют ni переменных на ячейку, где i = 2, ..., k, причем ячейки 1 типа являются ячейками IMPES, если существуют;
(d)(2) задают i равным единице,
(d)(3) генерируют li_N ограничительную матрицу Ri, где li - полное количество ячеек и N - полное количество переменных, в результате чего R1 выбирает переменные Множества 1,
(d)(4) задают i равным i плюс один,
(d)(5) генерируют li_N ограничительную матрицу Ri, которая выбирает переменные Множества i,
(d)(6) определяют заполненный ограничитель ![]()
(d)(7) если i не равно k, повторяют этапы (е)(4)-(е)(6), пока i не станет равным k,
e) применяют мультипликативную процедуру Шварца с наложением к приведенной матрице для получения предобработчика, и
f) находят неизвестные переменные с использованием предобработчика, полученного на этапе (e), и
g) повышают выход флюида в интересующей области с использованием моделирования коллектора.
20. Способ по п.19, в котором на этапе (d)(6) определения заполненного ограничителя дополнительно:
(d)(6) (i) задают
![]()
(d)(6) (ii) задают rpq(i) равным нулю, p в диапазоне значений 1, .. . ., li, и q в диапазоне значений 1, ..., N,
(d)(6) (iii) задают p равным 1,
(d)(6) (iv) задают q как неизвестный номер вектора решения, соответствующий переменному номеру p в Множестве i (vp(i)=xq),
(d)(6) (v) задают rpq(i) равным единице,
(d)(6) (vi) определяют, равно ли p величине li, и если нет, задают p равным p+1 и возвращаются к этапу (е)(6) (iv), а если p равно li, задают Ri равной
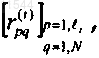
и
(d)(6) (vii) задают Pi равной RiT.
21. Способ по п.20, в котором на этапе (е) применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно:
(е)(1) задают i равным единице,
(е)(2) находят давления y во всех ячейках, с использованием уравнения ![]()
(е)(3) задают приближенное решение х равным ![]() и задают s равным
и задают s равным ![]()
(е)(4) определяют, равно ли i величине k, и если нет,
(е)(4) (i) задают i равным i плюс 1,
(е)(4) (ii) находят yi с использованием ![]()
(е)(4) (iii) используя новое значение yi, вычисляют новое значение x, равное х плюс ![]()
(е)(4) (iv) вычисляют новое значение si, равное s минус произведение ![]() и
и
(е)(4) (v) возвращаются к этапу определения (f)(4), пока i не станет равным k.
22. Способ по п.19, в котором общей переменной является давление.
23. Способ по п.19, в котором общей переменной является температура.
24. Способ по п.19, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием квази-IMPES приведения.
25. Способ по п.19, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием истинного IMPES приведения.
26. Устройство хранения программ, читаемое машиной, материально реализующее программу, состоящую из команд, выполняемых машиной для осуществления этапов способа осуществления моделирования коллектора с использованием модели коллектора, в которой на интересующую область наложена сетка, причем сетка интересующей области содержит один или несколько типов ячеек, причем типы ячеек различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной, способ содержит этапы, на которых:
a) идентифицируют разные типы ячеек для сетки,
b) строят общую матрицу для модели коллектора на основании разных типов ячеек,
c) по меньшей мере, частично отделяют общую переменную от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,
d) математически разбивают переменные в приведенной матрице на k подмножеств по типам ячейки,
e) применяют мультипликативную процедуру Шварца с наложением к приведенной матрице для получения предобработчика, и
f) используют предобработчик для нахождения неизвестных переменных.
27. Устройство хранения программ по п.26, в котором сетка является структурированной.
28. Устройство хранения программ по п.26, в котором сетка является неструктурированной.
29. Устройство хранения программ по п.26, в котором общей переменной является давление.
30. Устройство хранения программ по п.26, в котором общей переменной является температура.
31. Устройство хранения программ по п.26, в котором общую матрицу, построенную на этапе построения (b), записывают в блочном виде на основании количества типов ячеек в интересующей области.
32. Устройство хранения программ по п.26, в котором существует тип ячейки с одной переменной, и общей матрице [[А]] требуется одна строка блоков и один столбец блоков.
33. Устройство хранения программ по п.32 для каждой ячейки с одной переменной, общей матрице [[А]] требуется одна строка блоков и один столбец блоков, и для каждой ячейки с множественными переменными с одним столбцом блоков общей матрице [[А]] требуется две дополнительных строки блоков и два дополнительных столбца блоков.
34. Устройство хранения программ по п.26, в котором этап (с), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием квази-IMPES приведения.
35. Устройство хранения программ по п.26, в котором этап (с), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием истинного IMPES приведения.
36. Устройство хранения программ по п. 26, в котором на этапе (d) математического разбиения переменных в приведенной матрице дополнительно:
(d)(1) задают полное количество ячеек в интересующей области равным li, задают N равным полному количеству переменных, задают k равным количеству типов неявных ячеек плюс один, причем ячейки i типа имеют ni переменных на ячейку, где i = 2, ...., k, причем ячейки 1 типа являются ячейками IMPES, если существуют,
(d)(2) задают i равным единице,
(d)(3) генерируют li_N ограничительную матрицу Ri, где li - полное количество ячеек и N - полное количество переменных, в результате чего R1 выбирает переменные Множества 1,
(d)(4) задают i равным i плюс один,
(d)(5) генерируют li_N ограничительную матрицу Ri, которая выбирает переменные Множества i,
(d)(6) определяют заполненный ограничитель ![]() и
и
(d)(7) если i не равно k, повторяют этапы (е)(4)-(е)(6), пока i не станет равным k.
37. Устройсттю хранения программ по п.26, в котором на этапе (е) применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно
(е)(1) задают i равным единице,
(е)(2) находят давления y во всех ячейках, с использованием уравнения ![]()
(е)(3) задают приближенное решение x равным ![]() и задают s равным
и задают s равным ![]()
(е)(4) определяют, равно ли i величине k, и если нет,
(е)(4) (i) задают i равным i плюс 1,
(е)(4) (ii) находят yi с использованием ![]()
(е)(4) (iii) используя новое значение yi, вычисляют новое значение х, равное х плюс ![]()
(е)(4) (iv) вычисляют новое значение s, равное s минус произведение ![]() и
и
(е)(4) (v) возвращаются к этапу определения (f) (4), пока i не станет равным k.
38. Устройство моделирования, реагирующее на входные данные, приспособленное для решения системы нелинейных уравнений, которые представляют конкретную сущность, причем устройство моделирования генерирует множество результатов моделирования при решении системы нелинейных уравнений, причем множество результатов моделирования включает в себя один или несколько параметров, характеризующих конкретную сущность, в котором на представление сущности наложена сетка, причем сетка представления сущности содержит один или несколько типов ячеек, причем типы ячеек различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной, содержащее:
a) первое средство для идентификации разных типов ячеек для сетки,
b) второе средство для построения общей матрицы для модели коллектора на основании разных типов ячеек,
c) третье средство для, по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,
d) четвертое средство для математического разбиения переменных в приведенной матрице на k подмножеств по типам ячейки,
e) пятое средство для применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика, и
f) шестое средство для использования предобработчика для нахождения неизвестных переменных.
39. Устройство моделирования по п.38, в котором сетка является структурированной.
40. Устройство моделирования по п.38, в котором сетка является неструктурированной.
41. Устройство моделирования по п.38, в котором общей переменной является давление.
42. Устройство моделирования по п.38, в котором общая матрица, построенная вторым средством (b), записана в блочном виде, на основании количества типов ячеек в интересующей области.
43. Устройство моделирования по п.42, в котором существуеттип ячейки с одной переменной, и общей матрице [[А]] требуется одна строка блоков и один столбец блоков.
44. Устройство моделирования по п.43 для каждой ячейки с одной переменной, общей матрице [[А]] требуется одна строка блоков и один столбец блоков и для каждой ячейки с множественными переменными с одним столбцом блоков общей матрице [[А]] требуется две дополнительных строки блоков и два дополнительных столбца блоков.
45. Устройство моделирования по п.38, в котором третье средство (с), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице включает в себя средство для использования квази-IMPES приведения.
46. Устройство моделирования по п.38, в котором третье средство (с), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице включает в себя средство для использования истинного IMPES приведения.
47. Устройство моделирования по п.38, в котором четвертое средство (d) для математического разбиения переменных в приведенной матрице дополнительно содержит:
(d)(1) средство для задания полного количества ячеек в интересующей области равным li, задания N равным полному количеству переменных, задания k равным количеству типов неявных ячеек плюс один, причем ячейки i типа имеют ni переменных на ячейку, где i = 2, ..., k, причем ячейки 1 типа являются ячейками IMPES, если существуют,
(d)(2) средство для задания i равным единице,
(d)(3) средство для генерации li_N ограничительной матрицы Ri, где li - полное количество ячеек и N - полное количество переменных, в результате чего R1 выбирает переменные Множества 1;
(d)(4) средство для задания i равным i плюс один,
(d)(5) средство для генерации li_N ограничительной матрицы Ri, которая выбирает переменные Множества i,
(d)(6) средство для определения заполненного ограничителя ![]() и
и
(d)(7) средство для, если i не равно k, повторения этапов (е)(4)-(е)(6), пока i не станет равным k.
48. Устройство моделирования по п.38, в котором пятое средство (е) для применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно содержит:
(е)(1) средство для задания i равным единице,
(е)(2) средство для нахождения давлений у во всех ячейках, с использованием уравнения ![]()
(е)(3) средство для задания приближенного решения х равным ![]() и задания s равным
и задания s равным ![]()
(е)(4) средство для определения, равно ли i величине k, и если нет,
(е)(4) (i) средство для задания i равным i плюс 1,
(е)(4) (ii) средство для нахождения yi с использованием ![]()
(е)(4) (iii) средство для использования нового значения yi, вычисления нового значения х, равного х плюс ![]()
(е)(4) (iv) средство для вычисления нового значения s, равного s минус произведение ![]() и
и
(е)(4) (v) средство для возвращения к этапу определения (f)(4), пока i не станет равным k.
49. Устройство, реагирующее на множество входных данных для отображения сеточного представления геологического пласта, содержащее совокупность ячеек сетки и совокупность результатов моделирования, связанную, соответственно, с совокупностью ячеек, причем типы ячеек сетки различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной, содержащее
a) первое средство для идентификации разных типов ячеек для сетки, в котором сетка является неструктурированной,
b) второе средство для построения общей матрицы для модели коллектора на основании разных типов ячеек,
c) третье средство для, по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,
d) четвертое средство для математического разбиения переменных в приведенной матрице на k подмножеств по типам ячейки,
e) пятое средство для применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика, и
f) шестое средство для использования предобработчика для нахождения неизвестных переменных.
50. Устройство по п.49, в котором общей переменной является давление, и в котором четвертое средство (d) для математического разбиения переменных в приведенной матрице дополнительно содержит:
(d)(1) средство фыя задания полного количества ячеек в интересующей области равным li, задания N равным полному количеству переменных, задания k равным количеству типов неявных ячеек плюс один, причем ячейки i типа имеют ni переменных на ячейку, где i = 2, ..., k причем ячейки 1 типа являются ячейками IMPES, если существуют,
(d)(2) средство для задания i равным единице,
(d)(3) средство для генерации li_N ограничительной матрицы Ri, где li - полное количество ячеек и N - полное количество переменных, в результате чего R1 выбирает переменные Множества 1,
(d)(4) средство для задания i равным i плюс один,
(d)(5) средство для генерации li_N ограничительной матрицы Ri, которая выбирает переменные Множества i,
(d)(6) средство для определения заполненного ограничителя ![]() и
и
(d)(7) средство для, если i не равно k, повторения этапов (е)(4)-(е)(6), пока i не станет равным k.
51. Устройство по п.50, в котором пятое средство (е) для применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно содержит:
(е)(1) средство для задания i равным единице,
(е)(2) средство для нахождения давлений у во всех ячейках, с использованием уравнения ![]()
(е)(3) средство для задания приближенного решения х равным ![]() и задания s равным
и задания s равным ![]()
(е)(4) средство для определения, равно ли i величине k, и если нет,
(е)(4) (i) средство для задания i равным i плюс 1,
(е)(4) (ii) средство для нахождения yi с использованием ![]()
(е)(4) (iii) средство для использования нового значения yi, вычисления нового значения х, равного х плюс ![]()
(е)(4) (iv) средство для вычисления нового значения s, равного s минус произведение ![]() и
и
(е)(4) (v) средство для возвращения к этапу определения (f) (4), пока i не станет равным k.
Текст
011544 Область техники, к которой относится изобретение Данное изобретение относится к устройствам, способам и системам, используемым при моделировании коллектора. В частности, изобретение предусматривает способы, устройства и системы для более эффективного и экономичного моделирования потока флюидов в коллекторах с использованием мультипликативного метода Шварца с наложением для предварительной обработки адаптивных неявных линейных систем. Уровень техники Моделирование коллектора часто требует численного решения уравнений, описывающих физику сложного поведения многокомпонентного, многофазного потока флюидов в естественных поровых средах в коллекторе и других типов потока флюидов, где угодно в эксплуатационной системе. Определяющие уравнения, обычно используемые для описания потока флюидов, основаны на гипотезе термодинамического равновесия и законах сохранения массы, импульса и энергии, что описано в Aziz K. и SettariA., Petroleum Reservoir Simulation, Elsevier Applied Science Publishers, Лондон, 1979. Сложность физики,которая определяет поток флюидов в коллекторе, приводит к системам взаимосвязанных нелинейных уравнений в частных производных, которые не поддаются решению традиционными аналитическими методами. В результате, необходимы методы численного решения. Были разработаны различные математические модели, формулы, дискретные методы и стратегии решения, связанные с сеткой, наложенной на интересующую область коллектора. Подробное рассмотрение задач моделирования коллектора и уравнений, связанных с этими задачами, можно найти, например,в опубликованной патентной заявке РСТ ExxonMobil, международный номер публикации WO 01/40937,включенной сюда посредством ссылки, и в патенте США 6662146 В 1 ("патент '146"), включенном сюда посредством ссылки. Моделирование коллектора можно использовать для прогнозирования темпов добычи из коллекторов и можно использовать для определения соответствующих улучшений, например замены оборудования или бурения дополнительных скважин, которые можно реализовать для повышения отдачи. Сетка, наложенная на интересующую область в модели коллектора, может быть структурированной или неструктурированной. Такие сетки состоят из ячеек, причем каждая ячейка имеет одно или несколько неизвестных свойств, но все ячейки в сетке имеют одну общую неизвестную переменную, обычно давление. Другие неизвестные свойства могут включать в себя, но без ограничения, свойства флюидов,например водонасыщенность или температуру, или "свойства породы", например проницаемость или пористость и пр. Ячейка, рассматриваемая как имеющая только одну неизвестную переменную (обычно давление), именуется здесь "ячейкой с одной переменной" или "ячейкой IMPES", а ячейка с более чем одной неизвестной именуется здесь "ячейкой с множественными переменными" или "неявной ячейкой". Наиболее популярными подходами к решению нелинейных уравнений в дискретной форме являются системы FIM (полностью неявный метод) и IMPES (неявная переменная давления, явные переменные насыщенности), описанные в работе Peaceman, D., Fundamentals of Reservoir Simulation, опубликованнойElsevier Лондон, 1977, и Aziz K. и Settari A.: Petroleum Reservoir Simulation, Elsevier Applied Science Publishers, Лондон, 1979. существует большое количество конкретных построений FIM и IMPES, описанных в работе Coats, K.H.: "A Note on IMPES and Some IMPES-Based Simulation Models", SPEJ(5)3, (сентябрь 2000), стр. 245, включенной сюда посредством ссылки. Полностью неявный метод (FIM) предусматривает, что все переменные и коэффициенты, зависящие от этих переменных, обрабатываются неявно. В системе FIM все ячейки имеют фиксированное количество неизвестных, больше одной неизвестной, обозначенное здесь буквой "m". В результате, FIM является безусловно устойчивой, благодаря чему теоретически можно брать любой размер временного шага. Для каждого временного шага нужно решать взаимосвязанную систему нелинейных алгебраических уравнений с множественными степенями свободы (неявными переменными) на ячейку. Наиболее общим методом решения этих нелинейных систем уравнений является схема Ньютона-Рафсона, которая представляет собой метод итераций, где приближенное решение нелинейной системы получается посредством итерационного процесса линеаризации, решения и обновления линейной системы. Метод Ньютона-Рафсона предусматривает, что для f(x)=0, можно найти решение с использованием итерации: Из данной начальной точки для уравнения х = g(x) итерация xn+1=g(xn) будет сходиться к корню "а",если Моделирование в системе FIM требует большого объема вычислений. Линейная система уравнений с множественными неявными переменными на ячейку образуется при каждой итерации НыотонаРафсона. Эффективность построителя модели коллектора зависит, в большой степени, от способности решать эти линейные системы уравнений устойчиво и эффективно с вычислительной точки зрения. Согласно методу IMPES, только одна переменная, обычно давление, обрабатывается неявно. Все остальные переменные, включая, но без ограничения, переменные насыщенности и состава, обрабатываются в явном виде. Кроме того, переменные, связанные с потоком (проводимость), и капиллярное давление также обрабатываются в явном виде. Для каждой ячейки уравнения сохранения объединяют для-1 011544 получения уравнения давления. Эти уравнения образуют линейную систему взаимосвязанных уравнений, которую можно решить относительно неявной переменной, обычно давления. Получив давление,значения насыщенности и капиллярного давления обновляют в явном виде. Обработка в явном виде насыщенности (а также проводимости и капиллярного давления) приводит к условной устойчивости. Иными словами, максимально допустимый временной шаг в значительной степени зависит от характеристик задачи, например максимально допустимой пропускной способности и/или изменения насыщенности,для любой ячейки. Когда размер временного шага не является чрезмерно ограничительным, методIMPES чрезвычайно полезен. Дело в том, что линейная система уравнений имеет одну неявную переменную, обычно давление, на ячейку. Однако, в большинстве практических случаев, ограничения устойчивости, связанные с методом IMPES, приводят к непрактично малым временным шагам. Адаптивный неявный метод (AIM) был разработан для объединения большого размера временного шага FIM с низкой вычислительной нагрузкой IMPES. См. работу Thomas, G.W. и Thurnau, D.H, "Reservoir Simulation Using an Adaptive Implicit Method", SPEJ (октябрь, 1983), стр. 759 ("Томас и Турнау"),включенную сюда посредством ссылки. В системе AIM, ячейки сетки могут иметь переменное число неизвестных. Метод AIM основан на том наблюдении, что, в большинстве случаев, для конкретного временного шага лишь малая доля из полного количества ячеек в модели требует FIM-обработки, и что для подавляющего большинства ячеек пригодна более простая обработка IMPES. В системе AIM, построитель модели коллектора адаптивно и автоматически выбирает надлежащий уровень неявности переменных (например, давления, насыщенности) для каждой ячейки. (См. Томас и Турнау.) Строгий анализ устойчивости можно использовать для установления равновесия между размером временного шага и конечной долей ячеек, имеющих FIM-обработку. См. работу Coats, K.Н. "IMPES Stability: Selection of StableTimesteps", SPEJ (июнь 2003), стр. 181-187, включенную сюда посредством ссылки, однако компьютерное решение систем AIM может оказаться трудным и неэффективным ввиду переменного числа неизвестных на ячейку. В патенте '146 Уотса описана недавняя попытка решения этой задачи. Согласно патенту '146:"способ осуществления моделирования коллектора путем решения матричного уравнения, полученного смешанным неявно-IMPES методом (MUM). Уравнение MUM получается из ньютоновой итерации переменной неявной модели коллектора. Переменная неявная модель коллектора содержит совокупность ячеек, включающую в себя неявные ячейки и ячейки IMPES. Уравнение MUM включает в себя скалярное уравнение IMPES для каждой ячейки IMPES и систему неявных уравнений для каждой неявной ячейки."(Патент '146 в ст. 8, стр. 8-16) Патент '146 представляет "способ решения неявного линейного уравнения" в виде где А - известная матрица, С - известный вектор, и х - неизвестный вектор (патент '146, ст. 9, строки 62-66.) В патенте '146 раскрыты по меньшей мере три подхода к решению уравнения, полученного смешанным неявно-IMPES методом. Первый называется "первый метод линейного решателя", который включает в себя этапы:"1. Строят глобальное матричное уравнение давления IMPES из матричного уравнения, полученного смешанным неявно-IMPES методом. 2. Вычисляют коэффициенты для уравнений насыщенности (1.2.30) в неявных ячейках. 3. Решают глобальное матричное уравнение давления IMPES дляединого промежуточного давления в каждой ячейке в коллекторе и вычисляют изменения давления на основании промежуточных давленийи давленийпреобладающих в начале итерации. 4. Обновляют остатки неявного уравнения в неявных ячейках на основании изменений давления[этап 3] 5. В неявных ячейках получают улучшенные значения насыщенностииз уравнения насыщенности выведенных с использованием ограничения сохранения полной скорости между ячейками. 6. Обновляют остатки неявного уравнения в неявных ячейках и в полосе ячеек IMPES, которые находятся в потоковой связи с неявными ячейками, на основании решений относительно насыщенности,полученных на этапе 5. 7. Определяют выполнение условия сходимости" (Патент '146 от ст. 22, строка 59 по ст. 23, строка 28). См. также фиг. 6 А патента '146 и связанное с ней описание. Практик повторяет этапы 2-6, пока не будет выполнено условие сходимости (Патент 446 ст. 23 стр. 26-28). Второй способ патента '146 предусматривает следующие этапы: 1. Строят глобальное матричное уравнение давления IMPES из матричного уравнения, полученного смешанным неявно-IMPES методом. 2. Решают глобальное матричное уравнение давления IMPES относительно промежуточных давленийт.е. единого промежуточного давления в каждой ячейке в коллекторе и вычисляют изменения дав-2 011544 ленияна основании промежуточных давленийи давленийпреобладающих в начале итерации. 3. Вычисляют остатки неявного уравнения в неявных ячейках на основании изменений давления,вычисленных на этапе 2. 4. В неявных ячейках получают улучшенные значения насыщенностии вторые промежуточные давления,осуществляя одну или несколько итераций с помощью выбранного предобработчика 5. Обновляют остатки неявного уравнения в неявных ячейках и в полосе ячеек IMPES, которые находятся в потоковой связи с неявными ячейками, на основании улучшенных значений насыщенности и вторых промежуточных давлений, полученных на этапе 4. 6. Определяют выполнение условия сходимости.(Патент '146 ст. 24, строки 19-52.) См. также фиг. 6 В патента '146 и связанное с ней описание. Практик повторяет этапы 2-6, пока не будет выполнено условие сходимости. (Патент '146 ст. 24, строки 5152.) Третий способ патента '146 "эффективно требует неструктурированного решателя неявного уравнения." Этапы 1-3 и 6 третьего способа патента '146 такие же, как во втором способе. Этапы 4 ("4.sup.II) и 5("5.sup.II") третьего способа таковы: 4. Находят значения насыщенности S.sub.j.sup.n+2/3 и давления P.sub.j.sup.n+2/3 в неявных ячейках,одновременно поддерживая фиксированные давления в окружающей полосе (ячеек IMPES), равные значениям,определенным при определении давления методом IMPES. Любой метод можно использовать для генерации решений для значений насыщенностии давления , но он должен быть пригоден для неструктурированной формы неявных уравнений для ячеек. 5. Обновляют остатки в полосе ячеек IMPES. Поскольку неявные уравнения решены, их остатки будут удовлетворять критериям сходимости (Патент '146 ст. 25, строки 40-57). См. также фиг. 6 С патента'146 и связанное с ней описание. Однако современные подходы к решению этой задачи страдают существенными недостатками. Например, общеизвестно, что матрицы моделирования коллектора можно приближенно факторизовать наилучшим образом, если упорядочить их по ячейкам. Это значит, что все операции на этапе факторизации и предварительной обработки осуществляются как операции с субматрицами. Эти субматрицы имеют относительно малые размеры. Для матриц FIM с m неизвестными на блок, все эти субматричные блоки имеют порядок mm. Таким образом, для оптимальной эффективности короткие программные циклы для осуществления этих операций над блоками mm можно развертывать, для значительного увеличения общей скорости матричного решения. В отличие от субматричных блоков mm в системе FIM,этот подход развертки для систем AIM невозможно эффективно реализовать вследствие изменяющихся размеров субматричных блоков. В патенте '146 не раскрывается техника эффективной развертки для систем FIM или AIM. Кроме того, методы без пространственного наложения могут приводить к медленной сходимости. Такие методы требуют значительных вычислительных ресурсов, что повышает стоимость и снижает эффективность. В патенте '146 не раскрывается пространственное наложение. Настоящее изобретение предусматривает использование глобального матричного решения давления совместно с эффективной разверткой циклов, включающей в себя пространственное наложение, при осуществлении приближенной факторизации подсистемы с множественными переменными, в качестве предварительной обработки для систем AIM. Сущность изобретения В связи с вышеозначенными проблемами задачей настоящего изобретения является обеспечение способов, устройств и систем для более эффективного и экономичного моделирования потока флюидов в коллекторах с одновременным устранением или минимизации влияния вышеописанных проблем и ограничений. Другие задачи, признаки и преимущества настоящего изобретения очевидны специалистам в данной области техники из фигур, нижеследующего описания и формулы изобретения. Краткое описание чертежей Фиг. 1 а - представление коллектора. Фиг. 1b - детальный вид сечения коллектора, показанного на фиг. 1 а. Фиг. 2 - представление интересующей области в коллекторе, на которую наложена сетка, согласно предпочтительному варианту осуществления настоящего изобретения. Фиг. 3 - упрощенный, двухмерный вид интересующей области в коллекторе, на которую наложена сетка, согласно предпочтительному варианту осуществления настоящего изобретения. Фиг. 4 - логическая блок-схема предпочтительного варианта осуществления настоящего изобретения. Фиг. 5 - логическая блок-схема предпочтительного варианта осуществления этапа 250 на фиг. 4,применительно к квази-IMPES приведению. Фиг. 6 - логическая блок-схема альтернативного предпочтительного варианта осуществления этапа 250 на фиг. 4, применительно к истинному IMPES приведению.-3 011544 Фиг. 7 - представление интересующей области согласно предпочтительному варианту осуществления настоящего изобретения. Фиг. 8 - логическая блок-схема предпочтительного варианта осуществления настоящего изобретения для этапа построения k подмножеств (этап 260 на фиг. 4). Фиг. 9 - логическая блок-схема предпочтительного варианта осуществления этапа 745 на фиг. 8. Фиг. 10 - результат выбора ограничительного оператора Ri с использованием предпочтительного варианта осуществления настоящего изобретения и примера интересующей области, показанного на фиг. 7. Фиг. 11 - результат выбора ограничительного оператора Ri с использованием предпочтительного варианта осуществления настоящего изобретения и примера интересующей области, показанного на фиг. 7, где i равно двум. Фиг. 12 - результат выбора ограничительного оператора Ri с использованием предпочтительного варианта осуществления настоящего изобретения и примера, показанного на фиг. 7, где i равно трем. Фиг. 13 - логическая блок-схема детализированного варианта предпочтительного варианта осуществления этапа 770 на фиг. 8, который является этапом построения заполненного ограничителя Фиг. 14 - результат заполненного ограничителя но двум. применительно к примеру на фиг. 11, где i рав Фиг. 15 - результат 654 заполненного ограничителя применительно к примеру на фиг. 12, где i равно трем. Фиг. 16 - логическая блок-схема предпочтительного варианта осуществления этапа 270 на фиг. 4,изображающая использование k-блочного мультипликативного алгоритма Шварца с наложением для создания предобработчика. Подробное описание чертежей Нижеследующее подробное описание предпочтительных вариантов осуществления и других вариантов осуществления изобретения приведено со ссылкой на прилагаемые чертежи. Следует понимать,что специалисты в данной области техники могут предложить другие варианты осуществления и произвести изменения, не выходящие за рамки объема изобретения. Следующие термины определены ниже для пояснения и используются для описания чертежей и вариантов осуществления изобретения:"Ячейка IMPES": ячейка, имеющая только одну неизвестную переменную (обычно давление). Также именуется "ячейкой с одной переменной"."Неявная ячейка": ячейка, имеющая более одной неизвестной переменной. Также именуется "ячейкой с множественными переменными"."Ячейка с множественными переменными": ячейка, имеющая более одной неизвестной переменной. Также именуется "неявной ячейкой"."Ячейка с одной переменной": ячейка, обрабатываемая, как если бы она имела только одну неизвестную переменную (обычно давление). Также именуется "ячейкой IMPES". Для удобства описание разбито на разделы. Раздел 1 включает в себя общее описание предпочтительных вариантов осуществления настоящего изобретения. Раздел 2 - это описание построения k подмножеств согласно предпочтительному варианту осуществления настоящего изобретения. В разделе 3 рассматривается предварительная обработка согласно предпочтительному варианту осуществления настоящего изобретения. В разделе 4 рассматривается эффективная развертка циклов do согласно предпочтительному варианту осуществления настоящего изобретения. Раздел 5 содержит рассмотрение анализа ошибок. Раздел 1: Общее описание На фиг. 1 а показано представление коллектора 10 с сечением 12, которое показано на детальном(двухмерном) виде на фиг. 1b. Коллектор 10 (ниже водного зеркала) обычно содержит флюид 20, например нефть, газ, воду или смесь двух или трех из этих веществ, заполняющий поровые пространства между поровыми средами 30 (например, песчаником или известняком), которые составляют породу коллектора. На фиг. 2 показан трехмерный вид наложения сетки на интересующую область в коллекторе (не показана на фиг. 2) согласно предпочтительному варианту осуществления изобретения. (Конечно, "наложение сетки на интересующую область" означает наложение сетки на модель интересующей области,обычно хранящуюся на компьютерно-считываемых носителях, а не наложение физической сетки того или иного вида фона в интересующей области в самой земле.) Интересующая область 50 разбивается на ячейки 60. Хотя на фиг. 2 показана структурированная сетка, разбиение согласно настоящему изобретению может быть структурированным или неструктурированным. Коммерческие прикладные программы для разбиения интересующих областей, например GOCAD, FLOGRID и PETREL, общедоступны. На фиг. 3 показан упрощенный, двухмерный вид интересующей области 105 в коллекторе, разби-4 011544 том на ячейки, например ячейки 106, согласно предпочтительному варианту осуществления настоящего изобретения. В примере на фиг. 3 показаны разные типы ячеек, обозначенные разными штриховками. Каждая ячейка имеет одно или несколько неизвестных свойств, представленных переменными. Разные типы ячеек различаются количеством переменных, представляющих неизвестные свойства, которым обладают разные ячейки. Могут существовать неявные ячейки, имеющие более одной неизвестной переменной, и ячейки IMPES, которые, если присутствуют, имеют одну неизвестную переменную. В примере, показанном на фиг. 3, ячейки без штриховки ("ячейки IMPES" 110) имеют одно неизвестное свойство,представленное одной переменной, и ячейки с плотной штриховкой ("ячейки 2 типа" 120) имеют три неизвестных свойства, представленные тремя переменными. Одной общей неизвестной переменной обычно является давление, но может быть и какая-либо другая переменная. Ячейки 1 типа, если существуют, являются ячейками IMPES. Типы ячеек с множественными переменными здесь последовательно пронумерованы, начиная с двух, на основании их количества неизвестных переменных, причем ячейки 2 типа имеют наименьшее количество неизвестных переменных свыше одной, ячейки 3 типа имеют следующее в порядке возрастания количество неизвестных переменных, и т.д. в порядке возрастания количества неизвестных переменных. Хотя обычно имеется одна или несколько ячеек, имеющих только одну неизвестную переменную (ячейки IMPES), ячейки с только одной неизвестной переменной не обязаны присутствовать в сетке для практического осуществления настоящего изобретения. На фиг. 4 показана логическая блок-схема предпочтительного варианта осуществления настоящего изобретения. После начала 200, интересующая область в коллекторе выбирается 210 для моделирования. На интересующую область накладывается 220 сетка, состоящая из ячеек, имеющих неизвестные свойства, представленные переменными, причем каждая ячейка имеет одну общую неизвестную переменную. Обычно, как указано на этапе 220 на фиг. 4, общей неизвестной переменной является давление. Сетка может быть структурированной или неструктурированной. Разные типы ячеек, присутствующие в интересующей области, идентифицируются 230 на основании их количества неизвестных переменных. Согласно фиг. 4, строится 240 матрица, представляющая интересующую область на основании разных типов ячеек. В примере на фиг. 3, где в интересующей области 105 существует два типа ячеек, ячейки 1 типа 110, имеющие одну неизвестную переменную, и ячейки 2 типа 120, имеющие три неизвестные переменные, матрица A AIM будет записана в виде 33 блоков следующим образом: где s обозначает переменные, не связанные с давлением, в ячейках 2 типа 120, q обозначает давления в ячейках 2 типа 120 и е обозначает давления в ячейках 1 типа 110. Все переменные упорядочены по ячейкам, согласно вышеупомянутому разбиению матрицы. Для ячейки с одной переменной матрице А требуется одна строка блоков и один столбец блоков. Однако для каждой ячейки с множественными переменными матрице А требуется две дополнительных строки блоков и два дополнительных столбца блоков. В примере на фиг. 3, где имеется два типа ячеек,только один из которых является типом ячеек с множественными переменными, матрице А требуется,как описано выше, один столбец блоков и одна строка блоков для ячейки с одной переменной (ячейки 1 типа 110) и требуется две дополнительных строки блоков и два дополнительных столбца блоков для единственного типа ячеек с множественными переменными (ячейки 2 типа 120), всего три столбца блоков и три строки блоков. При наличии, например, трех типов ячеек, один из которых является 1 типом ячейки и остальные являются типами ячеек с множественными переменными, матрица А имела бы пять строк блоков и пять столбцов блоков. Следующее уравнение используется для нахождения неизвестных переменных, обозначенных x: где x - блочный вектор переменных, представляющих неизвестные свойства ячеек, и b - блочный вектор известных величин. Это то же самое уравнение, что и вышеприведенное Ур. 2 (согласно патенту'146), только "С" в Ур. 2 заменено буквой "b." Форма, приведенная в Ур. 4 выбрана потому, что она согласуется с другими документами и трудами авторов настоящего изобретения, но эти два уравнения идентичны. В Ур. 4 блочный вектор x и блочный вектор b имеют одинаковую длину. Длина блочного вектора x и блочного вектора b равна полному количеству ячеек в интересующей области. В примере,показанном на фиг. 3, где интересующая область 105 имеет десять ячеек в высоту и одиннадцать ячеек в ширину, длина обоих векторов x и b равна ста десяти, т.е. полному количеству ячеек. Согласно фиг. 4, следующий этап решения Ур. 4 состоит в, по меньшей мере, частичном отделении 250 давления от других переменных в матрице с использованием процесса приведения для получения приведенной матрицы. (Согласно вариантам осуществления, где общей неизвестной переменной является величина, отличная от давления, на этом этапе от других переменных будет, по меньшей мере, частично отделяться эта переменная (не давление. Известно много процессов приведения, которые можно-5 011544 использовать для отделения давления от других переменных согласно настоящему изобретению. Некоторые процессы приведения в ряде случаев могут оказаться предпочтительнее других. Два процесса приведения, которые можно использовать, это квази-IMPES приведение и истинное IMPES приведение, которые оба подробно описаны ниже. Истинное IMPES приведение обычно обеспечивает более симметричную матрицу давления, чем квази-IMPES. Квази-IMPES хорошо работает, если симметрия не очень важна для метода предварительной обработки. Однако некоторые методы предварительной обработки,например алгебраический многосеточный (AMG) метод предварительной обработки, эффективнее для симметричных и почти симметричных матриц, чем для несимметричных матриц. Соответственно, истинное IMPES будет предпочтительнее, например, когда для нахождения давления используется методAMG. При моделировании коллектора приведение IMPES широко используется для приближенного отделения давления от других переменных. В работе Wallis, J.R., Kendall, R.P. и Little, Т.Е.: "Constrained Residual Acceleration of Conjugate Residual Methods", SPE 13536, представленной на Симпозиуме SPE по моделированию коллектора, Хьюстон, Техас, фев. 10-13, 1985 (Wallis и др. 1985"), включенный сюда посредством ссылки, авторы используют алгебраическую процедуру в методе под названием "CPR." Метод CPR, описанный в упомянутой статье, применяется к линейным системам, связанным с FIM. Эта алгебраическая процедура именуется здесь "квази-IMPES приведением". На фиг. 5 показана логическая блок-схема предпочтительного варианта осуществления аспекта настоящего изобретения, реализующего квази-IMPES приведение. Квази-IMPES приведение описывается следующей матрицей масштабирования Q, где Q задается 252 в виде: и где и где diag(Aqs), diag(Ass) и diag(Aes) задают блочно-диагональные матрицы, состоящие из блоков главной диагонали Aqs, Ass и Aes соответственно. I это единичная матрица, имеющая единицы на диагоналях и нули во всех остальных позициях. Согласно фиг. 5, обе стороны Ур. 4, Ах = b, умножаются 253 на Q, в результате чего Ax = b приобретает вид: Приведенная матрица вычисляется как произведение матрицы масштабирования Q и матрицы А: и Истинное IMPES приведение это еще один процесс приведения, который можно осуществлять согласно настоящему изобретению. Предпочтительный вариант осуществления настоящего изобретения с использованием истинного IMPES приведения показан на фиг. 6. Истинное IMPES приведение рассмотрено в работе Stone, H.L. и Garder, Jr., A.O.: "Analysis of Gas-Cap or Dissolved-Gas Drive Reservoirs",AIME (1961), т. 222, включенной сюда посредством ссылки. Можно вычислить матрицу масштабирования истинного IMPES (обозначенную здесь Т). Согласно фиг. 6, после начала 255, Т задается 256 следующим образом: где colsum(Aqs), colsum(Ass) и colsum(Aes) задают блочно-диатональные матрицы, и где каждый диагональный блок равен сумме блоков в соответствующем столбце блоков Aqsr Ass и Aes соответственно. Согласно фиг. 6, обе стороны Ур. 4, Ах = b, умножаются 257 на Т для получения Ур. 8-6 011544 где и приведенная матрица А: Кроме того, на этапе 250 на фиг. 4 можно использовать другие типы приведения. Согласно фиг. 4, множество всех неизвестных переменных сетки разбивается 260 на некоторое количество подмножеств. Пусть k - количество типов неявных ячеек плюс один, причем "один" представляет глобальное множество, обычно с одной общей неизвестной переменной, обычно давлением. Напомним, что неявные ячейки - это ячейки, имеющие более одной неизвестной переменной. k подмножеств могут пересекаться. Раздел 2 содержит описание предпочтительного варианта осуществления этапа 260 на фиг. 4 для построения k подмножеств. Предобработчики применяются к уравнениям для облегчения их решения. Для построения предобработчика для Ур. 8 применяется (этап 280 на фиг. 4) мультипликативная процедура Шварца с наложением, которая может принимать различные формы. Это подробно описано в разделе 3. Раздел 2. Разбиение интересующей области на k подмножеств На фиг. 7 показана интересующая область 605, имеющая ячейки 1 типа с одной неизвестной переменной, ячейки 2 типа с тремя неизвестными переменными и ячейки 3 типа с четырьмя неизвестными переменными. В примере на фиг. 7 существует три разных типа ячеек; в результате, k равно трем, где k количество типов неявных ячеек плюс один. Напомним, что неявный тип ячейки - это тип ячейки с более чем одной неизвестной переменной на ячейку. Неизвестные переменные для ячеек обозначаются буквами, расположенными в соответствующих ячейках 606. В примере на фиг. 7 неизвестная переменная давления, в общем случае, обозначена Р, и неизвестные переменные, не связанные с давлением, например значения насыщенности, состава, температуры, в общем случае, обозначены X1, Х 2, , Хn. В примере на фиг. 7 ячейки 1 типа 610 обозначены только Р 608; ячейки 2 типа 620 (т.е. с тремя неизвестными переменными, с шаблоном 25% штриховки) обозначены Р, X1 612 (для нефтенасыщенности) и Х 2 613 (для водонасыщенности), и ячейки 3 типа 625 (т.е. с четырьмя неизвестными переменными, с шаблоном точечной штриховки на фиг. 7) обозначены Р, X1, Х 2 и Х 3 622 (для температуры). На фиг. 8 показана логическая блок-схема предпочтительного варианта осуществления настоящего изобретения для этапа построения k подмножеств (этап 260 на фиг. 4). Начиная 700 с этапа 250 на фиг. 4 положим 710, что полное количество ячеек в интересующей области равно l1, положим, что Nполное количество переменных, и положим, что k равно количеству типов неявных ячеек плюс один. Ячейки i типа имеют ni переменных на ячейку, где i = 2, . , k. Ячейки 1 типа - это ячейки IMPES (если существуют). В примере, показанном на фиг. 7, l1 равно 110, N равно 188 и k равно 3. Положим 720, что i равно 1. Генерируем 725 ограничительную матрицу R1, которая выбирает Множество 1, содержащее множество переменной давления (или, в других вариантах осуществления, какой-либо другой общей неизвестной переменной, если это не давление) для всех имеющихся ячеек, включая ячейки IMPES, если существуют. Это позволяет выбирать все ячейки в интересующей области. Чтобы это работало правильно, общая неизвестная переменная (в этом примере давление) должна находиться в первой позиции в каждой ячейке. Если общая неизвестная переменная находится в другой позиции, алгоритм придется соответственно изменить. На фиг. 9 А показан детализированный вариант этапа 725 (для i равного единице) и этапа 745 (для i большего единицы), представленных на фиг. 8. Начиная 800 с этапа 720 на фиг. 8, для этапа 725 (или с этапа 740 на фиг. 8, для этапа 745). Положим 810: Задаем 812 rpq(i) равным нулю, р в диапазоне значений 1 li; и q в диапазоне значений 1, , N. Полагаем 814 р равным 1. Задаем 816 q как неизвестный номер вектора решения, соответствующий переменному номеру р в Множестве i (vp(1) = xq). Задаем 818 rpq(i) равным единице. Определяем 820, равно ли р величине li. Если нет, задаем 822 р равным р + 1 и возвращаемся к этапу 816. Если р равно li, задаем 824 Ri равной Задаем 826 Pi равной RiT и возвращаемся к фиг. 8 (к этапу 740, если использовать фиг. 9 для этапа 725, или к этапу 765, если использовать фиг. 9 для этапа 745). На фиг. 10 показан результат выбора ограничительного оператора R1 с использованием примера,показанного на фиг. 7. Использование ограничительного оператора R1 в этом примере дает Множество 1 630, где давление является единственной неизвестной переменной. Выбирается каждая ячейка 606, в которой давление 608 является неизвестной переменной, будь то ячейка 635 только с одной неизвестной переменной или ячейка 640, 645 с более чем одной неизвестной. Согласно фиг. 8, задаем 740 i равным i плюс один. Генерируем 745 liN ограничительную матрицуRi, которая выбирает переменные Множества i, где Множество i содержит множество li переменных, определенное hi переменными для каждой ячейки типа i и nj переменными любой ячейки типа j (где j меньше i), которая имеет соседнюю ячейку типа i, совместно с ней использующую более чем одну точку. На фиг. 9 изображена подробная логическая блок-схема для предпочтительного варианта осуществления этапа 745 на фиг. 8. Ячейки j типа, имеющие соседей типа i, называются здесь "соседними ячейками". Переменные упорядочиваются по ячейкам. На фиг. 11 показан результат 650 выбора ограничительного оператора R1 с использованием примера, показанного на фиг. 7, где i равно двум. На фиг. 11, как и на фиг. 7, ячейки 1 типа, например 610, обозначены только Р; ячейки 2 типа, например 620, (т.е. с тремя неизвестными переменными) обозначены посредством Р, X1 и Х 2, и ячейки 3 типа 625 (т.е. с четырьмя неизвестными переменными) обозначены посредством Р, X1, Х 2 и Х 3. Поскольку i равно двум, выбираются ячейки 2 типа, например 620. Кроме того, выбираются соседние ячейки, которые являются ячейками типа j, где j меньше i, и которые граничат с ячейками 2 типа в более чем одной точке. В этом случае ячейки j типа представляют собой ячейки 1 типа, которые граничат с ячейками 2 типа в более чем одной точке, например 640. Все R2 выбранных ячеек показаны с 25% шаблоном, независимо от их количества переменных. Аналогично, на фиг. 12 показан результат 652 выбора ограничительного оператора Ri с использованием примера, показанного на фиг. 7, где i равно трем. На фиг. 12, как и на фиг. 7, ячейки 1 типа 610 обозначены только Р, ячейки 2 типа, например 620, обозначены посредством Р, X1 и Х 2, и ячейки 3 типа,например 625, обозначены посредством Р, X1, Х 2 и Х 3. Выбираются все ячейки 3 типа. Ячейки, соседствующие с ячейками 3 типа, будучи ячейками j типа, где j меньше i, например 670, 675, также выбираются. Все R3 выбранных ячеек показаны с точечным шаблоном, независимо от их количества переменных. Согласно фиг. 8, после выбора ячеек i типа и их соответствующих соседних ячеек j типа следующий этап состоит в добавлении надлежащего количества фиктивных переменных в соседние ячейки, путем построения 765 заполненного ограничителя Детализированный вариант этапа 770 показан на фиг. 13 и рассмотрен ниже. Согласно фиг. 8, если 780 i не равно k, то возвращаемся к этапу 740. Если i равно k, то переходим 795 к этапу 270 на фиг. 4. Хотя, согласно фиг. 8, начальное значение i равно единице на этапе 720 и далее i увеличивается в этом примере (см. этап 740) до тех пор, пока i не станет равным к (см. этап 780), методология этих этапов(т.е. порядок выбора значения i для генерации соответствующих ограничительных матриц) независима от порядка. В других вариантах осуществления можно начинать с i, равного k, и далее уменьшать i, покаi не достигнет единицы, или переходить к выбору i в любом другом порядке. На фиг. 13 показан детализированный вариант предпочтительного варианта осуществления этапа 770 на фиг. 8, который представляет собой этап построения заполненного ограничителя Заполненный ограничитель, при необходимости, добавляет фиктивные переменные в выбранные соседние ячейки. Вспомним из этапа 826 на фиг. 9, что Pi равна RiT, где RiT получена транспонированиемRi. Начиная 850 с этапа 745 на фиг. 8, задаем 852 i равным двум. Полагаем 854 li равным количеству переменных в Множестве i, mi - количеству ячеек, представленных переменными Множества i, и hi - количеству неизвестных для ячеек i типа. Полагаем 856 q равным единице. Полагаем 858 Cq равным номеру ячейки в Множестве i, которая содержит переменную номер q ("q-ячейки"), и полагаем Dq равным неизвестному номеру в ячейке Cq, соответствующему номеру q переменной. Полагаем 860, что spq(i) - это элементы (mini)li матрицы, Si. Определяем 862 равно ли р величине: (Cq - 1)ni+ Dq. Если нет, то задаем 864spq(i) равным нулю. Если да, то задаем 866 spq(i) равным единице. Определяем 868, равно ли q величине li. Если q не равно li, задаем 870 q равным q плюс 1 и возвращаемся к этапу 858. Если q равно li, то определяем 872, равно ли р величине mini. Если р не равно mini, задаем р равным р плюс один и возвращаемся к как произведение Si и Ri и полагаем этапу 858. Если р равно mini, то вычисляем 876 понированной матрице Генерируем 878 заполненную матрицу Шварца: равной транс задаем число, отличное от нуля,и для каждой нулевой строки (строки со всеми нулями) в(1) на ее главной диагонали. Матрица Di представляет эти диагональные элементы, добавленные во избежание сингулярности вследствие добавления фиктивных уравнений и переменных. Определяем 880,равно ли i величине k. Если i не равно k, задаем 882 i равным i плюс один и возвращаемся к этапу 854. Если i равно k, то переходим к этапу 780 на фиг. 8. Напомним, что общая переменная (обычно давление) предпочтительно всегда находится в первой позиции в каждой ячейке; если она не находится в первой позиции, то в алгоритмы может потребоваться внести соответствующие изменения. На фиг. 14 показан результат 651 заполненного ограничителя применительно к фиг. 11, при i равном двум. На фиг. 14, как и на фиг. 11 и фиг. 7, ячейки 1 типа, например 610, обозначены только Р, ячейки 2 типа, например 620, (т.е. с тремя неизвестными переменными) обозначены посредством Р, X1 и Х 2,-8 011544 и ячейки 3 типа 625 (т.е. с четырьмя неизвестными переменными) обозначены Р, X1, Х 2 и Х 3. Посколькуi равно двум, ячейки 2 типа, например 620, выбраны на фиг. 11, совместно с соседними ячейками, например 640, которые являются ячейками j типа, где j меньше i, и которые граничат с ячейками 2 типа в более чем одной точке. Как и на фиг. 11, все R2 выбранных ячеек показаны с 25% шаблоном, независимо от их количества переменных. Теперь, согласно фиг. 14, фиктивные ячейки, обозначенные символом D,добавлены к соседним ячейкам, которые были выбраны, например 640, в результате чего выбранные соседние ячейки имеют такое же количество переменных, как выбранные ячейки 2 типа, т.е. с тремя переменными. На фиг. 15 показан результат 654 заполненного ограничителя применительно к фиг. 12, при i равном трем. На фиг. 15, как и на фиг. 12 и фиг. 7, ячейки 1 типа 610 обозначены только Р, ячейки 2 типа,например 620, обозначены посредством Р, X1 и Х 2, и ячейки 3 типа, например 625, обозначены посредством Р, X1, Х 2 и Х 3. Поскольку i равно трем, все ячейки 3 типа выбраны на фиг. 12 совместно с ячейками, соседствующими с ячейками 3 типа, которые являются ячейками j типа, где j меньше i, и которые граничат с ячейками 3 типа в более чем одной точке. Поскольку i равно трем для фиг. 12, j равно одному или двум, поэтому выбираются ячейки 1 и 2 типов, соседствующие с ячейками 3 типа, например ячейка 2 типа 670 и ячейка 1 типа 675. Как и на фиг. 12, все R3 выбранных ячеек показаны с точечным шаблоном,независимо от их количества переменных. Теперь, согласно фиг. 15, фиктивные ячейки, обозначенные символом D, добавлены к соседним ячейкам, которые были выбраны, например 670, 675, в результате чего выбранные соседние ячейки имеют такое же количество переменных, как выбранные ячейки 3 типа,т.е. с четырьмя переменными. Раздел 3: Предварительная обработка Раздел 3, вариант 1: использование мультипликативного алгоритма Шварца с наложением На фиг. 16 показана логическая блок-схема предпочтительного варианта осуществления этапа 270,представленного на фиг. 4, применительно к использованию нашего мультипликативного алгоритма Шварца с наложением для создания предобработчика. Остаточный вектор можно представить в виде Где- самый последний вектор приближенного решения. Пусть М-1 - матрица, приближенно обратная Предварительно обработанный остаток используется для улучшения приближения х: Это тот же самый х, что и в Ур. 4, но усилия здесь направлены на получение приближенных решений для x. Временная переменная s используется для поддержки промежуточных остатков, и yi это промежуточное решение для всех неизвестных переменных в подпространстве Vi. Использование мультипликативной предварительной обработки Шварца с наложением можно задать следующими этапами. Согласно фиг. 16, начинаем 400 с этапа 260 на фиг. 4. На начальном этапе задаем 410 i равным единице. Находим 420 давления у во всех ячейках, с использованием уравнения и задаем 430 приближенное решение х равным: и задаем 430 Определяем 440, равно ли i величине k. Если i равно k, то переходим 450 к этапу 280 на фиг. 4. Если Используя новое значение yi, вычисляем 480 новое значение x равное x плюс Затем вычисляем 490 новое значение s в виде: Возвращаемся к этапу 440, повторяем этапы 440-480, пока i не станет равным k. Затем переходим 450 к этапу 280 на фиг. 4. Раздел 3, вариант 2: использование мультипликативного алгоритма Шварца с наложением с неточными локальными решениями В практических применениях уравнения 20 и 22 можно заменять неточными локальными решениями. Примеры включают в себя, но без ограничения, блок ILU(K), вложенную факторизацию, линейно решение Гаусса-Зейделя или предварительно обработанное итерационное решение с использованием методов ускорения, например GMRES или ORTHOMIN. См. Y. Saad и М. Н. Schultz.: "GMRES: a generalized minimal residual algorithm for solving nonsymmetric linear systems", SIAM Journal on Scientific and Statistical Computing, 7, стр. 856-869, 1986; Vinsome, "P.K.W: "Orthomin, an Iterative Method for Solving SparseSets of Simultaneous Linear Equations", SPE 5729, представленную на четвертом симпозиуме по числен-9 011544 ному моделированию отдачи коллектора сообщества инженеров-нефтяников AIME, находящемся в ЛосАнджелесе, Калифорния, фев. 19-20, 1976, все включенные посредством ссылки. Раздел 4. Эффективная развертка В предпочтительных вариантах осуществления изобретения эффективность повышается с использованием методов эффективной развертки цикла. ЗаполненнаяAIM субматрица разлагается на фиксированные неявные nini субматричные блоки. факторизуется или приближенно факторизуется с использованием операций с Таким образом субматрицами с фиксированным размером блока. Кроме того, на этапе решения или приближенного реприменяются операции с субматрицами с фиксированным разшения с использованием множителей мером блока. Эти операции с субматрицами осуществляются с высокой эффективностью благодаря развертке внутренних циклов do (т.е. полной записи кода вместо использования циклов do), связанных с размером блока ni. Введение фиктивных переменных и уравнений приводит к тому, что факторизованные матрицы имеют субматричные блоки фиксированного размера и делает развертку практичной для предварительной обработки AIM. Метод развертки особенно полезен при реализации этапов 420 и 470 на фиг. 16, которые являются наиболее вычислительно-сложными этапами на фиг. 16. Этот метод развертки цикла также можно использовать на других этапах изобретения, чтобы также повысить эффективность. Например, группируя по этим группам, можно создать субматричные блоки, котовсе ячейки одного типа и затем разлагая рые, в свою очередь, можно разложить на малые субматричные блоки фиксированного размера. Эффективное использованием этих подблоков на этапе умножения матрицы на вектор на этапе 490 на фиг. 16 предусматривает развертку циклов, длина которых связана с малыми размерами этих подблоков. Для программной реализации AIM, субматрицаi = 2, , k разлагается на фиксированные неявные nini субматричные блоки, которые используются во всех факторизациях или приближенных факторизациях и на этапах предварительной обработки Шварца. Эти операции с субматрицами могут выполняться с высокой эффективностью благодаря развертке внутренних циклов, связанных с размером блока ni. Раздел 5: Анализ ошибок Ниже приведен анализ ошибок метода, использующий мультипликативный алгоритм Шварца без наложения, аналогичный тому, который можно использовать согласно патенту 146. Ур. 8 можно записать в виде: Следующая система со вспомогательной матрицей А эквивалентна исходной системе: Эту вспомогательную матрицу А можно приближенно факторизовать в виде: Как показано ниже, применение такого метода приводит к замедлению сходимости и, в большинст- 10011544 ве случаев, занимает больше компьютерного времени, чем использование настоящего изобретения. Теперь опишем анализ ошибок мультипликативного метода Шварца с наложением согласно предпочтительному варианту осуществления настоящего изобретения. разлагается в виде 44 блока: где Ass и Aqq те же самые, что в Ур. 3. Блок Aee в Ур. 3, в свою очередь, делится на две части: явные ячейки, имеющие по меньшей мере одну неявную соседнюю ячейку (Abb), и не имеющие неявных соседей (Aii). Для двухблочного мультипликативного метода Шварца с наложением определим операторы пролонгации R1 и R2 в виде: где Is, Iq, Ib и Ii - единичные конформные матрицы для разбиения Следующая система со вспомогательной матрицей А эквивалентна исходной системе: Эту вспомогательную матрицу можно приближенно факторизовать в виде: где и матрица ошибки имеет вид: Таким образом, при наличии точного решения на обоих перекрывающихся подпространствах,единственная остаточная ошибка связана с неграничными явными ячейками при наличии явных соседей граничной ячейки. Эти ошибочные члены обычно много меньше ошибочных членов в Ур. 27. Поскольку последние ошибочные члены имеют дополнительные связи с переменными, не связанными с давлением. Заметим также, что на этапе сокращения IMPES предпринимаются попытки сократить именно эти связи давления с переменными, не связанными с давлением. Хотя вышеприведенное описание обеспечено в целях иллюстрации, объяснения и подробного описания некоторых вариантов осуществления изобретения автоматизированной инспекции дефектов микроструктуры повторяющегося массива, специалисты в данной области могут предложить модификации и адаптации описанных способов, систем и другие варианты осуществления и реализовать их без отхода от объема и сущности изобретения. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ осуществления моделирования коллектора, содержащий этапы, на которых:a) строят модель коллектора интересующей области путем наложения сетки на интересующую область, причем сетка содержит один или несколько типов ячеек, причем типы ячеек различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной,b) идентифицируют разные типы ячеек для сетки,c) строят общую матрицу для модели коллектора на основании разных типов ячеек,d) по меньшей мере, частично отделяют общую переменную от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,e) математически разбивают переменные в приведенной матрице на k подмножеств по типам ячейки, иf) применяют мультипликативную процедуру Шварца с наложением к приведенной матрице для получения предобработчика,g) находят неизвестные переменные с использованием предобработчика, полученного на этапе (f), иh) повышают выход флюида в интересующей области с использованием моделирования коллектора. 2. Способ по п.1, в котором на этапе построения (b) получают структурированные сетки. 3. Способ по п.1, в котором на этапе построения (b) получают неструктурированные сетки. 4. Способ по п.1, в котором общей переменной является давление. 5. Способ по п.1, в котором общей переменной является температура. 6. Способ по п.1, в котором общую матрицу, построенную на этапе построения (с), записывают в блочном виде, на основании количества типов ячеек в интересующей области. 7. Способ по п.6, в котором существует тип ячейки с одной переменной и общей матрице А требуется одна строка блоков и один столбец блоков. 8. Способ по п.6, в котором для каждой ячейки с одной переменной, общей матрице А требуется одна строка блоков и один столбец блоков и для каждой ячейки с множественными переменными с одним столбцом блоков общей матрице А требуется две дополнительных строки блоков и два дополнительных столбца блоков. 9. Способ по п.1, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием квази-IMPES приведения. 10. Способ по п.1, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием истинного IMPES приведения. 11. Способ по п.1, в котором на этапе (е) математического разбиения переменных в приведенной матрице дополнительно:(е)(1) задают полное количество ячеек в интересующей области равным li, задают N равным полному количеству переменных, задают k равным количеству типов неявных ячеек плюс один, причем ячейкиi типа имеют ni переменных на ячейку, где i = 1, 2, , k, причем ячейки 1 типа являются ячейками IMPES,если существуют,(е)(2) задают i равным единице,- 12011544(е)(3) генерируют liN ограничительную матрицу Ri, где li - полное количество ячеек и N - полное количество переменных, в результате чего R1 выбирает переменные Множества 1,(е)(4) задают i равным i плюс один,(е)(5) генерируют liN ограничительную матрицу Ri, которая выбирает переменные Множества i,(е)(6) определяют заполненный ограничитель,(е)(7) если i не равно k, повторяют этапы (е)(4)-(е)(6), пока i не станет равным k. 12. Способ по п.11, в котором на этапе (е)(6) определения заполненного ограничителя дополнительно(е)(6) (ii) задают rpq(i) равным нулю, p в диапазоне значений 1, , li; и q в диапазоне значений 1, , N,(е)(6) (iii) задают p равным 1,(е)(6) (iv) задают q как неизвестный номер вектора решения, соответствующий переменному номеру р в Множестве i (vp(i)=xq),(е)(6) (v) задают rpq(i) равным единице,(е)(6) (vi) определяют, равно ли p величине li, и если нет, задают р равным p + 1 и возвращаются к этапу (е)(6)(iv), а если p равно li, задают Ri равной(е)(6) (vii) задают Pi равной RiT. 13. Способ по п.1, где на этапе (f) применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно:(f)(3) задают приближенное решение x равным(f)(4) (iii) используя новое значение yi, вычисляют новое значение x, равное x плюс и(f)(4) (iv) вычисляют новое значение s, равное s минус произведение(f)(4) (v) возвращаются к этапу определения (f) (4), пока i не станет равным k. 14. Способ по п.1, в котором существует k-1 разных типов ячеек с m1 и на этапе (е) математического разбиения переменных в приведенной матрице дополнительно:(е)(1) для каждой ячейки типа mi1, i=1k-1 формируют подсистему, содержащую ячейки типа mi и их соседи другого типа, причем каждая подсистема имеет постоянный размер блока,(е)(2) для соседей типа nmi выбирают m общих переменных при построении подсистем, и(е) (3) для nm, выбирают все n переменных и заполняют систему m-n фиктивными переменными. 15. Способ по п.1, в котором общей переменной является давление, и в котором общую матрицу,построенную на этапе построения (с), записывают в блочном виде, на основании количества типов ячеек в интересующей области. 16. Способ по п.15, в котором для каждой ячейки с одной переменной, общей матрице А требуется одна строка блоков и один столбец блоков, и для каждой ячейки с множественными переменными с одним столбцом блоков общей матрице А требуется две дополнительных строки блоков и два дополнительных столбца блоков. 17. Способ по п.16, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием истинного IMPES приведения. 18. Способ по п.16, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием квази-IMPES приведения. 19. Способ осуществления моделирования коллектора, с использованием модели коллектора интересующей области, причем на интересующую область наложена сетка, причем сетка интересующей области содержит один или несколько типов ячеек, причем типы ячеек различаются количеством неизвест- 13011544 ных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной, содержащий этапы, на которых:a) идентифицируют разные типы ячеек для сетки,b) строят общую матрицу для модели коллектора на основании разных типов ячеек,c) по меньшей мере, частично отделяют общую переменную от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,d) математически разбивают переменные в приведенной матрице на k подмножеств по типам ячейки, при этом дополнительно:(d)(1) задают полное количество ячеек в интересующей области равным li, задают N равным полному количеству переменных, задают k равным количеству типов неявных ячеек плюс один, причем ячейкиi типа имеют ni переменных на ячейку, где i = 2, , k, причем ячейки 1 типа являются ячейками IMPES,если существуют;(d)(2) задают i равным единице,(d)(3) генерируют liN ограничительную матрицу Ri, где li - полное количество ячеек и N - полное количество переменных, в результате чего R1 выбирает переменные Множества 1,(d)(4) задают i равным i плюс один,(d)(5) генерируют liN ограничительную матрицу Ri, которая выбирает переменные Множества i,(d)(6) определяют заполненный ограничитель(d)(7) если i не равно k, повторяют этапы (е)(4)-(е)(6), пока i не станет равным k,e) применяют мультипликативную процедуру Шварца с наложением к приведенной матрице для получения предобработчика, иf) находят неизвестные переменные с использованием предобработчика, полученного на этапе (e), иg) повышают выход флюида в интересующей области с использованием моделирования коллектора. 20. Способ по п.19, в котором на этапе (d)(6) определения заполненного ограничителя дополнительно:(d)(6) (ii) задают rpq(i) равным нулю, p в диапазоне значений 1,. ., li, и q в диапазоне значений 1, , N,(d)(6) (iii) задают p равным 1,(d)(6) (iv) задают q как неизвестный номер вектора решения, соответствующий переменному номеру p в Множестве i (vp(i)=xq),(d)(6) (v) задают rpq(i) равным единице,(d)(6) (vi) определяют, равно ли p величине li, и если нет, задают p равным p+1 и возвращаются к этапу (е)(6) (iv), а если p равно li, задают Ri равной(d)(6) (vii) задают Pi равной RiT. 21. Способ по п.20, в котором на этапе (е) применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно:(е)(3) задают приближенное решение х равным(е)(4) (iii) используя новое значение yi, вычисляют новое значение x, равное х плюс и(е)(4) (iv) вычисляют новое значение si, равное s минус произведение(е)(4) (v) возвращаются к этапу определения (f)(4), пока i не станет равным k. 22. Способ по п.19, в котором общей переменной является давление. 23. Способ по п.19, в котором общей переменной является температура. 24. Способ по п.19, в котором этап (d), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием квази-IMPES приведения. 25. Способ по п.19, в котором этап (d), по меньшей мере, частичного отделения общей переменной- 14011544 от других неизвестных переменных в матрице осуществляют с использованием истинного IMPES приведения. 26. Устройство хранения программ, читаемое машиной, материально реализующее программу, состоящую из команд, выполняемых машиной для осуществления этапов способа осуществления моделирования коллектора с использованием модели коллектора, в которой на интересующую область наложена сетка, причем сетка интересующей области содержит один или несколько типов ячеек, причем типы ячеек различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной, способ содержит этапы, на которых:a) идентифицируют разные типы ячеек для сетки,b) строят общую матрицу для модели коллектора на основании разных типов ячеек,c) по меньшей мере, частично отделяют общую переменную от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,d) математически разбивают переменные в приведенной матрице на k подмножеств по типам ячейки,e) применяют мультипликативную процедуру Шварца с наложением к приведенной матрице для получения предобработчика, иf) используют предобработчик для нахождения неизвестных переменных. 27. Устройство хранения программ по п.26, в котором сетка является структурированной. 28. Устройство хранения программ по п.26, в котором сетка является неструктурированной. 29. Устройство хранения программ по п.26, в котором общей переменной является давление. 30. Устройство хранения программ по п.26, в котором общей переменной является температура. 31. Устройство хранения программ по п.26, в котором общую матрицу, построенную на этапе построения (b), записывают в блочном виде на основании количества типов ячеек в интересующей области. 32. Устройство хранения программ по п.26, в котором существует тип ячейки с одной переменной,и общей матрице А требуется одна строка блоков и один столбец блоков. 33. Устройство хранения программ по п.32 для каждой ячейки с одной переменной, общей матрице А требуется одна строка блоков и один столбец блоков, и для каждой ячейки с множественными переменными с одним столбцом блоков общей матрице А требуется две дополнительных строки блоков и два дополнительных столбца блоков. 34. Устройство хранения программ по п.26, в котором этап (с), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием квази-IMPES приведения. 35. Устройство хранения программ по п.26, в котором этап (с), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице осуществляют с использованием истинного IMPES приведения. 36. Устройство хранения программ по п. 26, в котором на этапе (d) математического разбиения переменных в приведенной матрице дополнительно:(d)(1) задают полное количество ячеек в интересующей области равным li, задают N равным полному количеству переменных, задают k равным количеству типов неявных ячеек плюс один, причем ячейкиi типа имеют ni переменных на ячейку, где i = 2, , k, причем ячейки 1 типа являются ячейками IMPES,если существуют,(d)(2) задают i равным единице,(d)(3) генерируют liN ограничительную матрицу Ri, где li - полное количество ячеек и N - полное количество переменных, в результате чего R1 выбирает переменные Множества 1,(d)(4) задают i равным i плюс один,(d)(5) генерируют liN ограничительную матрицу Ri, которая выбирает переменные Множества i,(d)(6) определяют заполненный ограничитель и(d)(7) если i не равно k, повторяют этапы (е)(4)-(е)(6), пока i не станет равным k. 37. Устройство хранения программ по п.26, в котором на этапе (е) применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно(е)(3) задают приближенное решение x равным(е)(4) (iii) используя новое значение yi, вычисляют новое значение х, равное х плюс и(е)(4) (iv) вычисляют новое значение s, равное s минус произведение(е)(4) (v) возвращаются к этапу определения (f) (4), пока i не станет равным k. 38. Устройство моделирования, реагирующее на входные данные, приспособленное для решения системы нелинейных уравнений, которые представляют конкретную сущность, причем устройство моделирования генерирует множество результатов моделирования при решении системы нелинейных уравнений, причем множество результатов моделирования включает в себя один или несколько параметров,характеризующих конкретную сущность, в котором на представление сущности наложена сетка, причем сетка представления сущности содержит один или несколько типов ячеек, причем типы ячеек различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной, содержащее:a) первое средство для идентификации разных типов ячеек для сетки,b) второе средство для построения общей матрицы для модели коллектора на основании разных типов ячеек,c) третье средство для, по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,d) четвертое средство для математического разбиения переменных в приведенной матрице на k подмножеств по типам ячейки,e) пятое средство для применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика, иf) шестое средство для использования предобработчика для нахождения неизвестных переменных. 39. Устройство моделирования по п.38, в котором сетка является структурированной. 40. Устройство моделирования по п.38, в котором сетка является неструктурированной. 41. Устройство моделирования по п.38, в котором общей переменной является давление. 42. Устройство моделирования по п.38, в котором общая матрица, построенная вторым средством(b), записана в блочном виде, на основании количества типов ячеек в интересующей области. 43. Устройство моделирования по п.42, в котором существует тип ячейки с одной переменной, и общей матрице А требуется одна строка блоков и один столбец блоков. 44. Устройство моделирования по п.43 для каждой ячейки с одной переменной, общей матрице А требуется одна строка блоков и один столбец блоков и для каждой ячейки с множественными переменными с одним столбцом блоков общей матрице А требуется две дополнительных строки блоков и два дополнительных столбца блоков. 45. Устройство моделирования по п.38, в котором третье средство (с), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице включает в себя средство для использования квази-IMPES приведения. 46. Устройство моделирования по п.38, в котором третье средство (с), по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице включает в себя средство для использования истинного IMPES приведения. 47. Устройство моделирования по п.38, в котором четвертое средство (d) для математического разбиения переменных в приведенной матрице дополнительно содержит:(d)(1) средство для задания полного количества ячеек в интересующей области равным li, задания N равным полному количеству переменных, задания k равным количеству типов неявных ячеек плюс один,причем ячейки i типа имеют ni переменных на ячейку, где i = 2, , k, причем ячейки 1 типа являются ячейками IMPES, если существуют,(d)(2) средство для задания i равным единице,(d)(3) средство для генерации liN ограничительной матрицы Ri, где li - полное количество ячеек иN - полное количество переменных, в результате чего R1 выбирает переменные Множества 1;(d)(4) средство для задания i равным i плюс один,(d)(5) средство для генерации liN ограничительной матрицы Ri, которая выбирает переменные Множества i,(d)(6) средство для определения заполненного ограничителя и(d)(7) средство для, если i не равно k, повторения этапов (е)(4)-(е)(6), пока i не станет равным k. 48. Устройство моделирования по п.38, в котором пятое средство (е) для применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно содержит:(е)(1) средство для задания i равным единице,(е)(2) средство для нахождения давлений у во всех ячейках, с использованием уравнения(е)(3) средство для задания приближенного решения х равным(е)(4) средство для определения, равно ли i величине k, и если нет,(е)(4) (i) средство для задания i равным i плюс 1,(е)(4) (ii) средство для нахождения yi с использованием(е)(4) (iii) средство для использования нового значения yi, вычисления нового значения х, равного х плюс и(е)(4) (iv) средство для вычисления нового значения s, равного s минус произведение(е)(4) (v) средство для возвращения к этапу определения (f)(4), пока i не станет равным k. 49. Устройство, реагирующее на множество входных данных для отображения сеточного представления геологического пласта, содержащее совокупность ячеек сетки и совокупность результатов моделирования, связанную, соответственно, с совокупностью ячеек, причем типы ячеек сетки различаются количеством неизвестных переменных, представляющих свойства ячеек, но каждая ячейка имеет общую переменную в качестве неизвестной переменной, содержащееa) первое средство для идентификации разных типов ячеек для сетки, в котором сетка является неструктурированной,b) второе средство для построения общей матрицы для модели коллектора на основании разных типов ячеек,c) третье средство для, по меньшей мере, частичного отделения общей переменной от других неизвестных переменных в матрице с использованием процесса приведения для получения приведенной матрицы,d) четвертое средство для математического разбиения переменных в приведенной матрице на k подмножеств по типам ячейки,e) пятое средство для применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика, иf) шестое средство для использования предобработчика для нахождения неизвестных переменных. 50. Устройство по п.49, в котором общей переменной является давление, и в котором четвертое средство (d) для математического разбиения переменных в приведенной матрице дополнительно содержит:(d)(1) средство для задания полного количества ячеек в интересующей области равным li, задания N равным полному количеству переменных, задания k равным количеству типов неявных ячеек плюс один,причем ячейки i типа имеют ni переменных на ячейку, где i = 2, , k причем ячейки 1 типа являются ячейками IMPES, если существуют,(d)(2) средство для задания i равным единице,(d)(3) средство для генерации liN ограничительной матрицы Ri, где li - полное количество ячеек иNполное количество переменных, в результате чего R1 выбирает переменные Множества 1,(d)(4) средство для задания i равным i плюс один,(d)(5) средство для генерации liN ограничительной матрицы Ri, которая выбирает переменные Множества i,и(d)(6) средство для определения заполненного ограничителя(d)(7) средство для, если i не равно k, повторения этапов (е)(4)-(е)(6), пока i не станет равным k. 51. Устройство по п.50, в котором пятое средство (е) для применения мультипликативной процедуры Шварца с наложением к приведенной матрице для получения предобработчика дополнительно содержит:(е)(1) средство для задания i равным единице,(е)(2) средство для нахождения давлений у во всех ячейках, с использованием уравнения(е)(3) средство для задания приближенного решения х равным(е)(4) средство для определения, равно ли i величине k, и если нет,(е)(4) (i) средство для задания i равным i плюс 1, и задания s равным(е)(4) (ii) средство для нахождения yi с использованием(е)(4) (iii) средство для использования нового значения yi, вычисления нового значения х, равного х плюс(е)(4) (iv) средство для вычисления нового значения s, равного s минус произведение(е)(4) (v) средство для возвращения к этапу определения (f) (4), пока i не станет равным k.
МПК / Метки
МПК: G06F 17/50
Метки: линейных, шварца, устройство, улучшения, моделирования, обработки, коллектора, система, систем, адаптивных, использованием, способ, предварительной, мультипликативной, наложением, неявных
Код ссылки
<a href="https://eas.patents.su/26-11544-ustrojjstvo-sposob-i-sistema-dlya-uluchsheniya-modelirovaniya-kollektora-s-ispolzovaniem-multiplikativnojj-predvaritelnojj-obrabotki-shvarca-s-nalozheniem-dlya-adaptivnyh-neyavnyh.html" rel="bookmark" title="База патентов Евразийского Союза">Устройство, способ и система для улучшения моделирования коллектора с использованием мультипликативной предварительной обработки шварца с наложением для адаптивных неявных линейных систем</a>
Предыдущий патент: Способ измерения перемещения объекта
Следующий патент: Способ управления системой лифтов и система лифтов