Многомасштабный способ конечных объёмов для использования при моделировании подземного течения

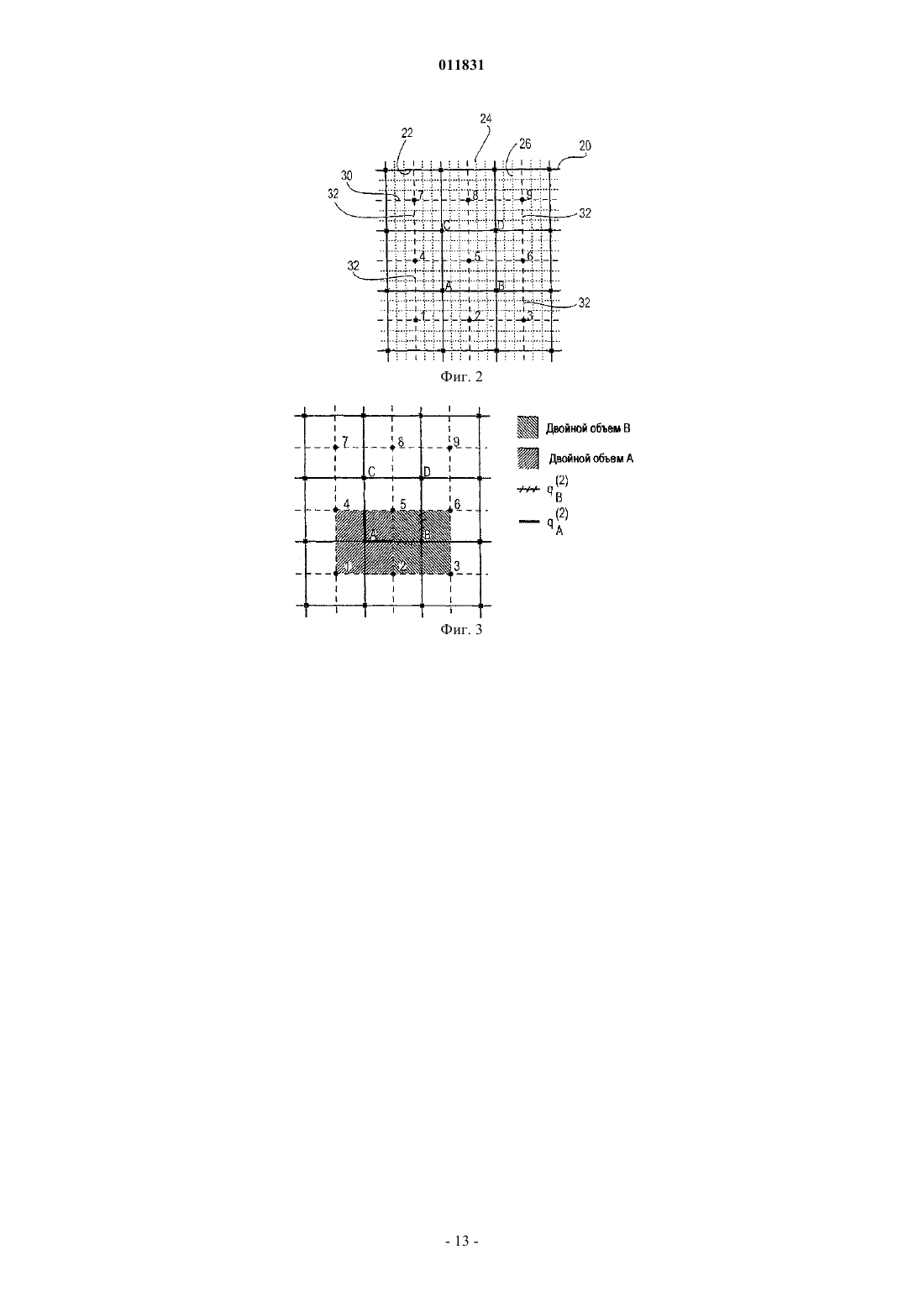
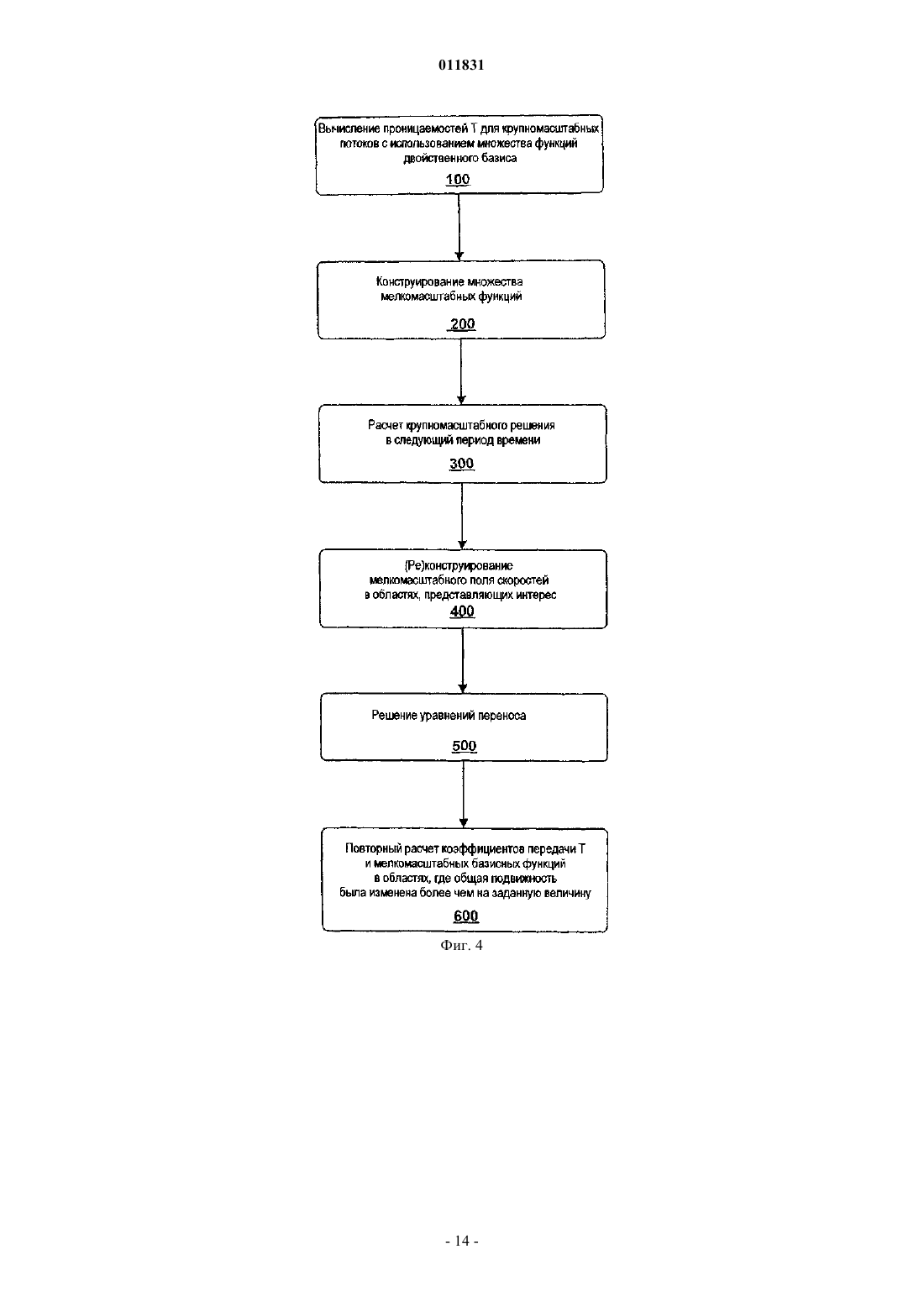
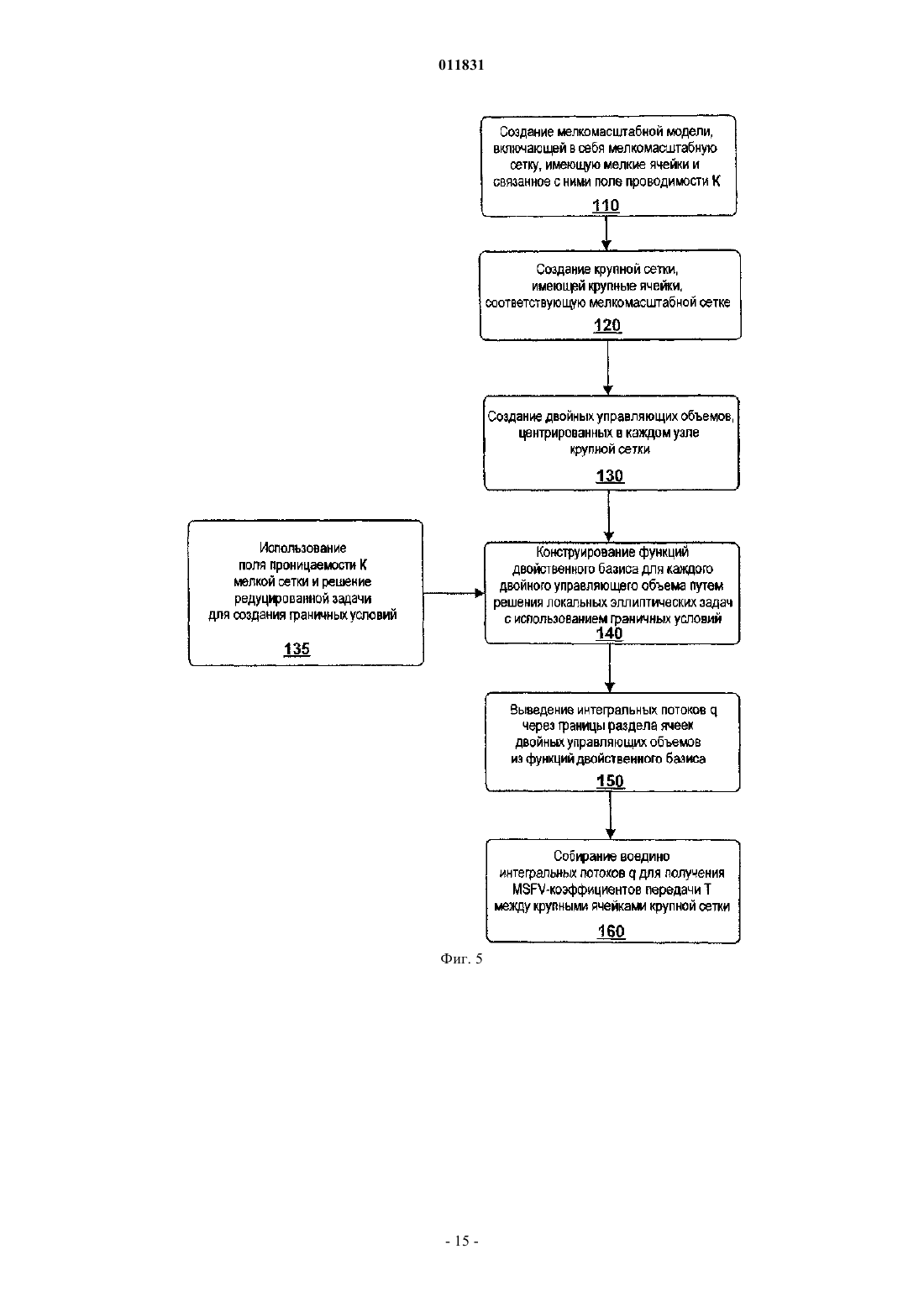
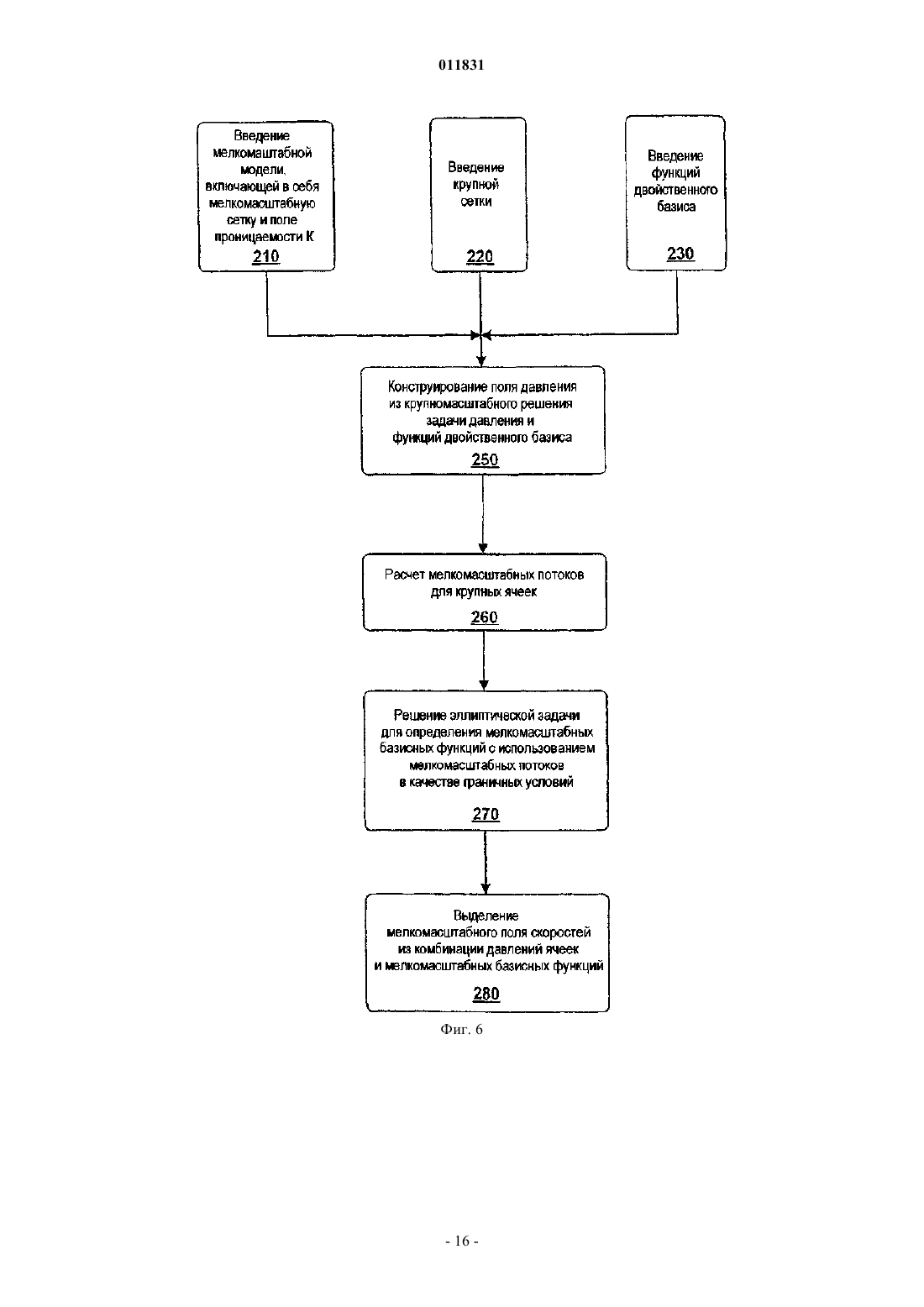
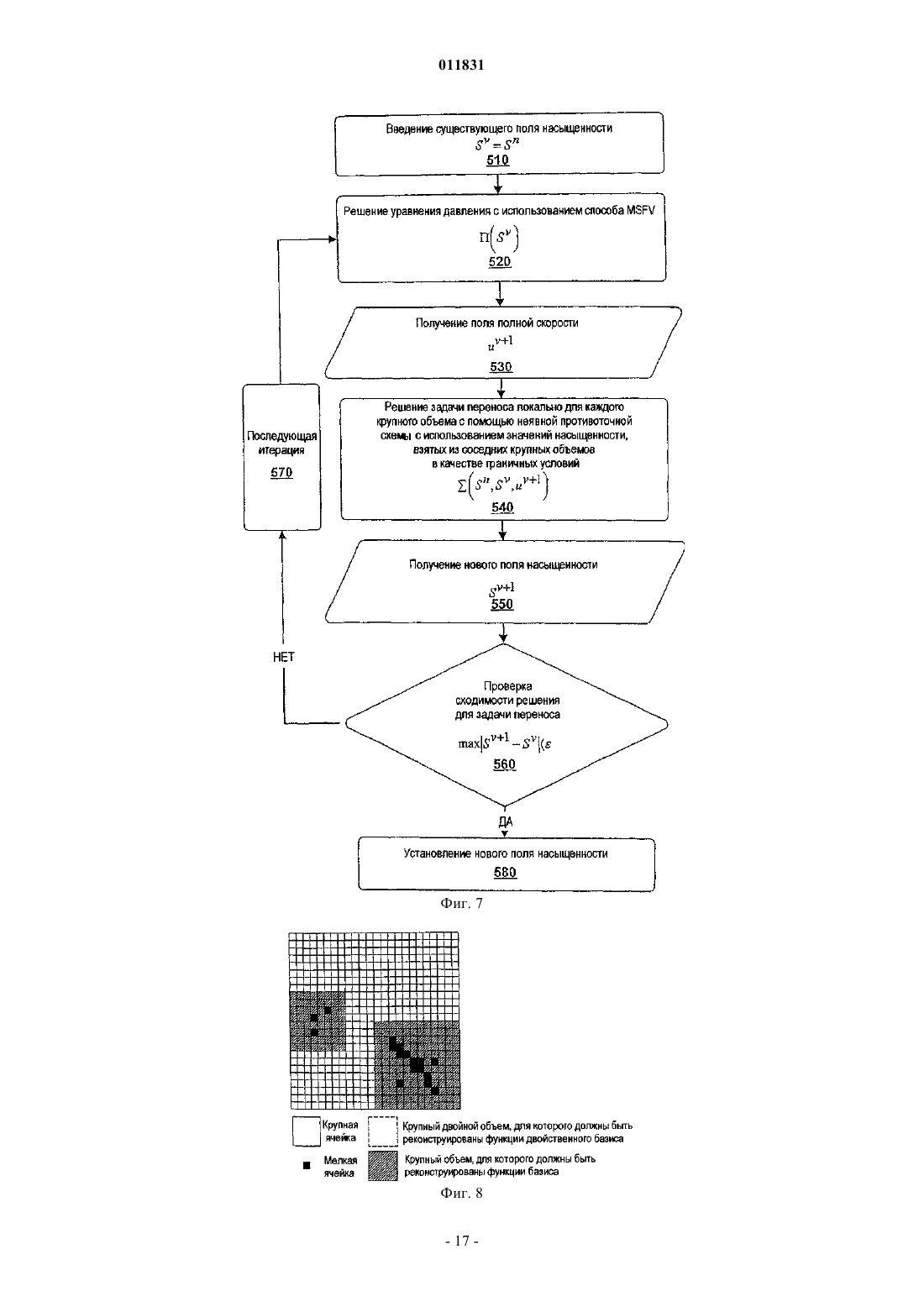
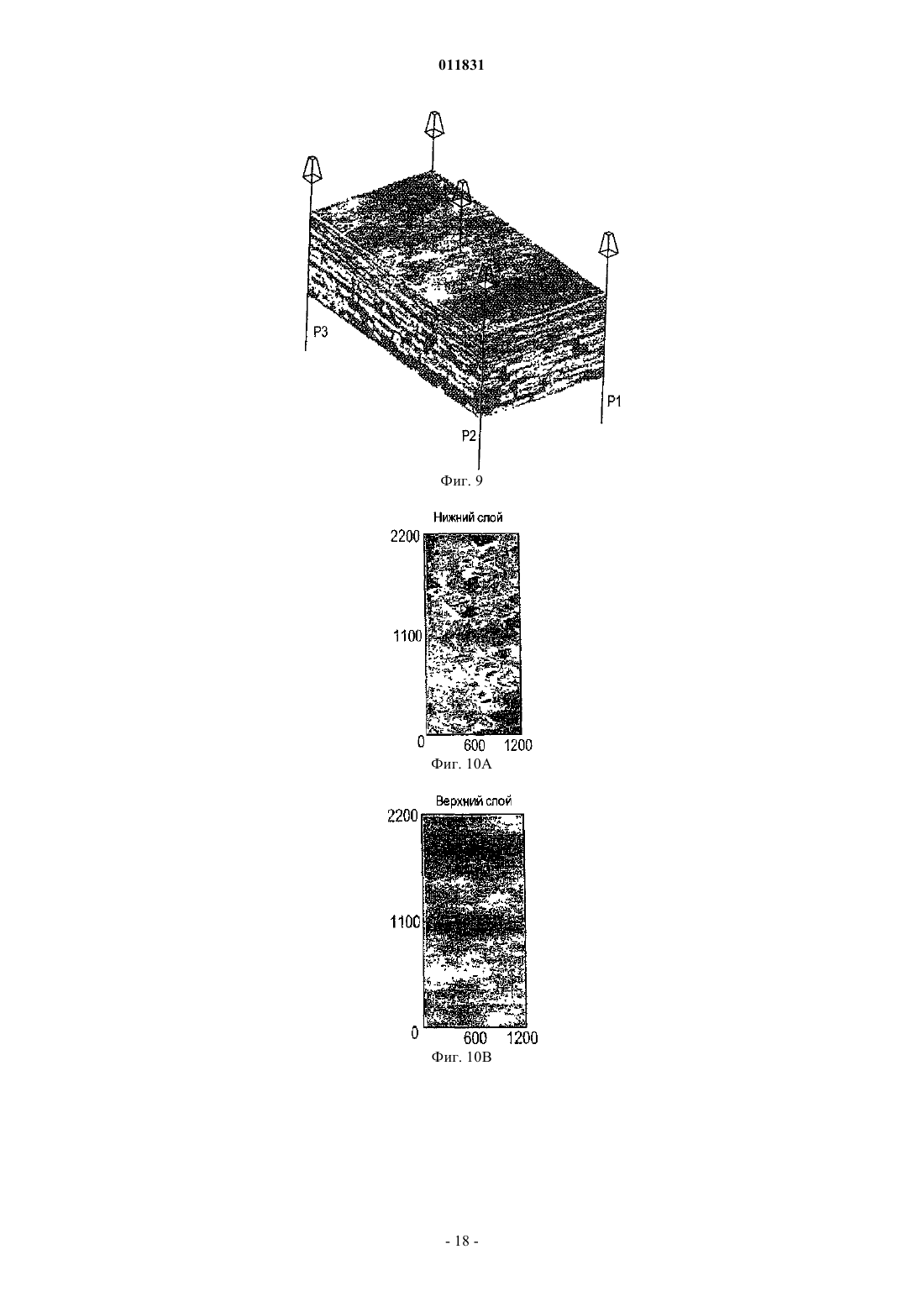
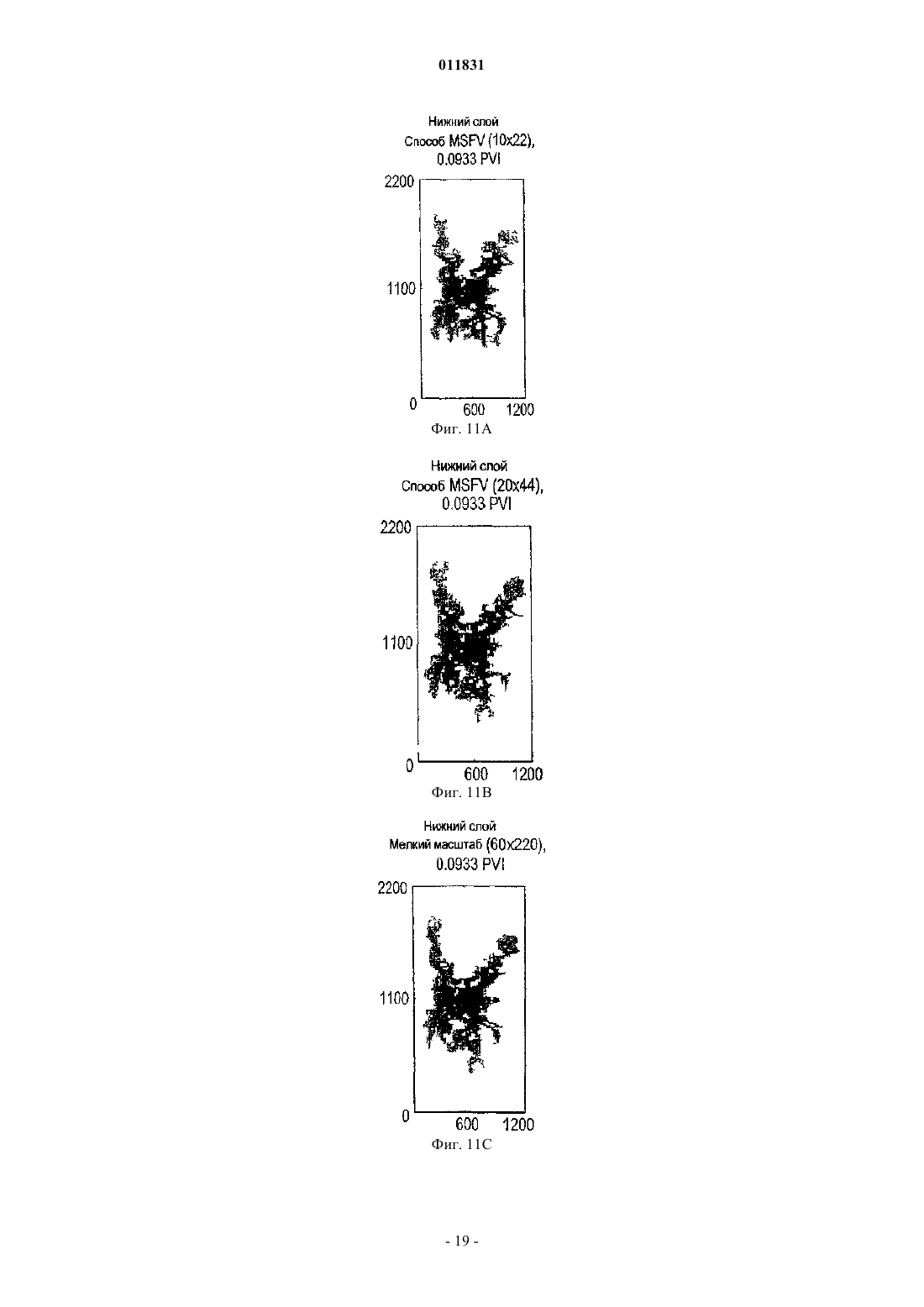
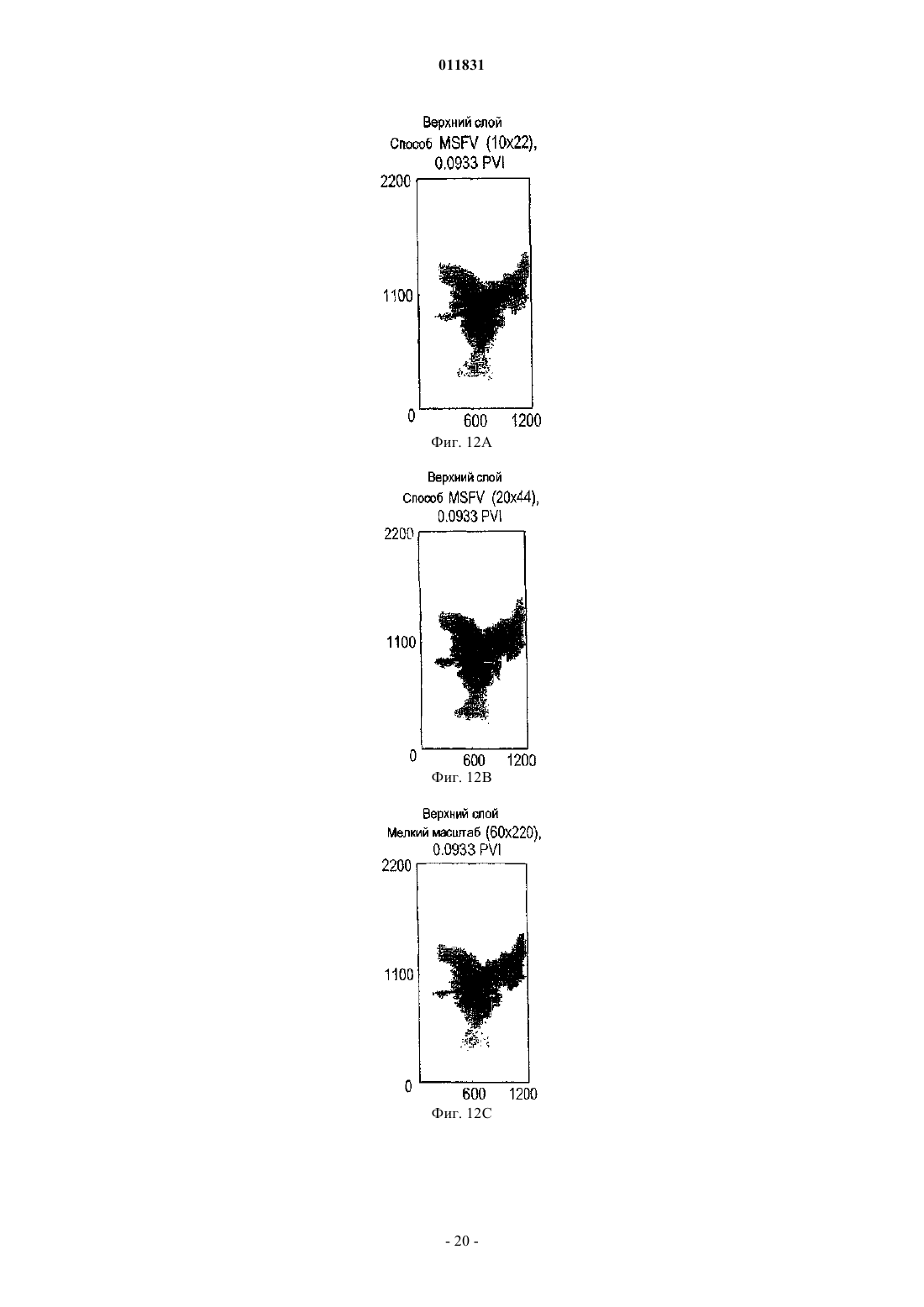
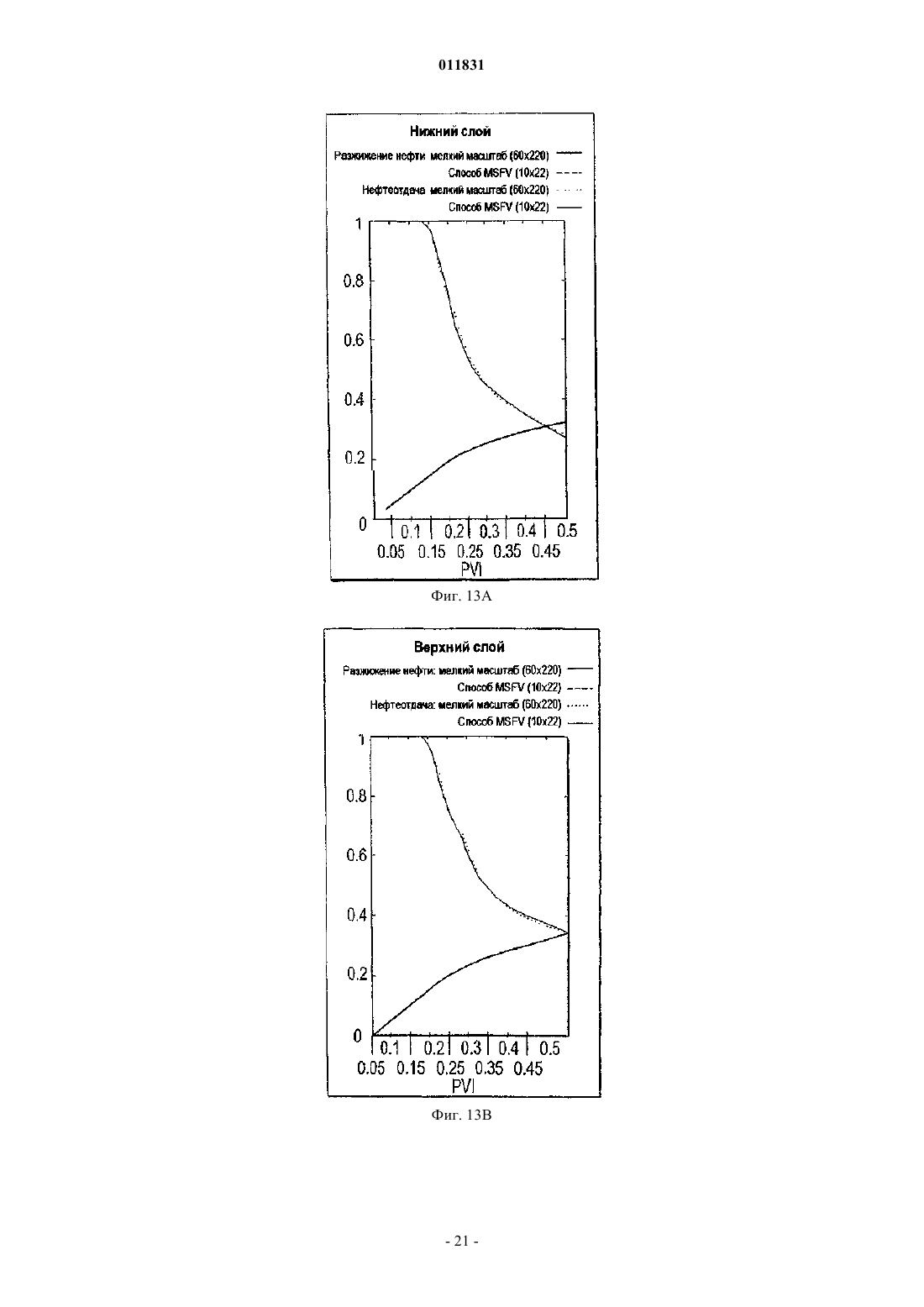
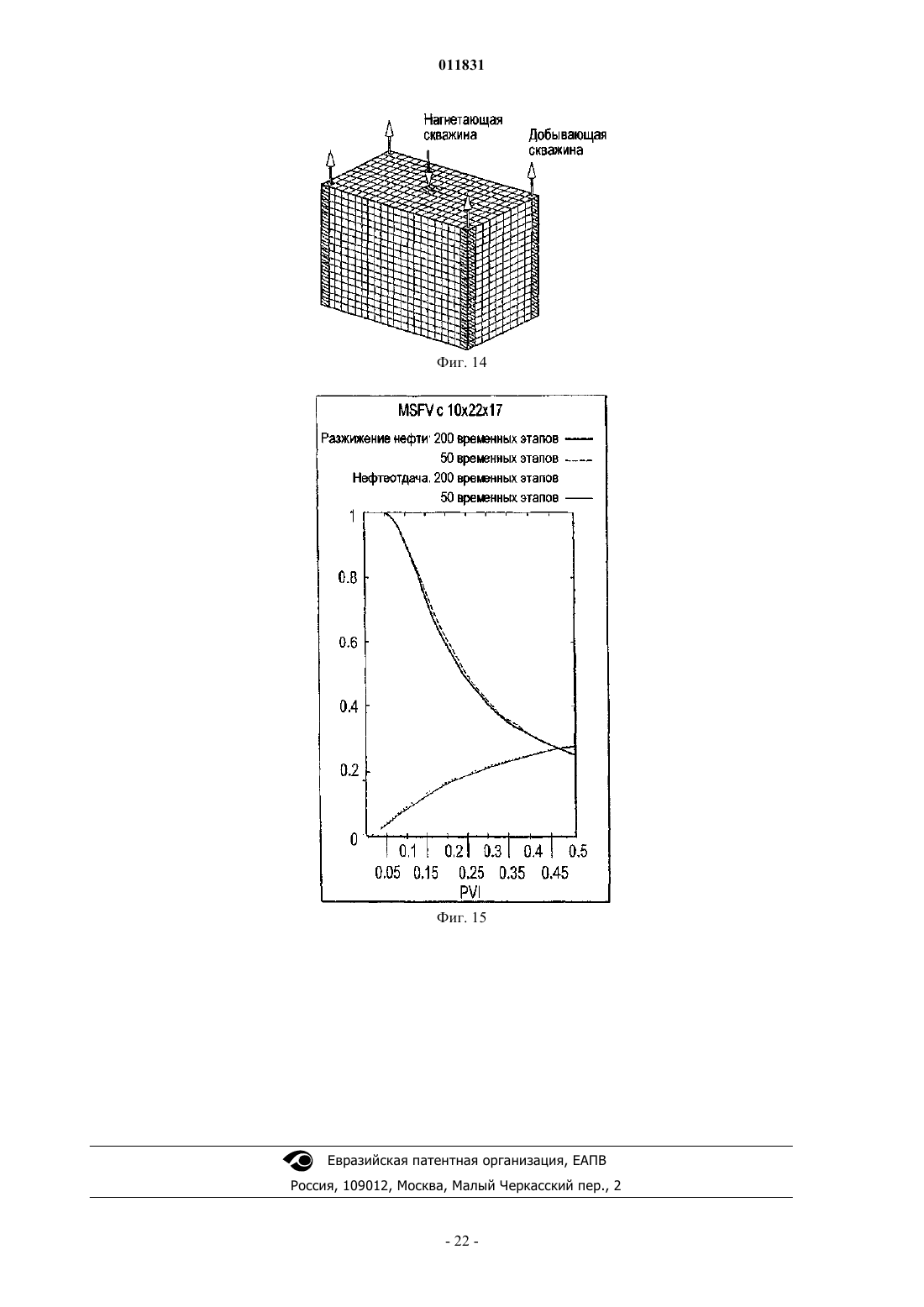
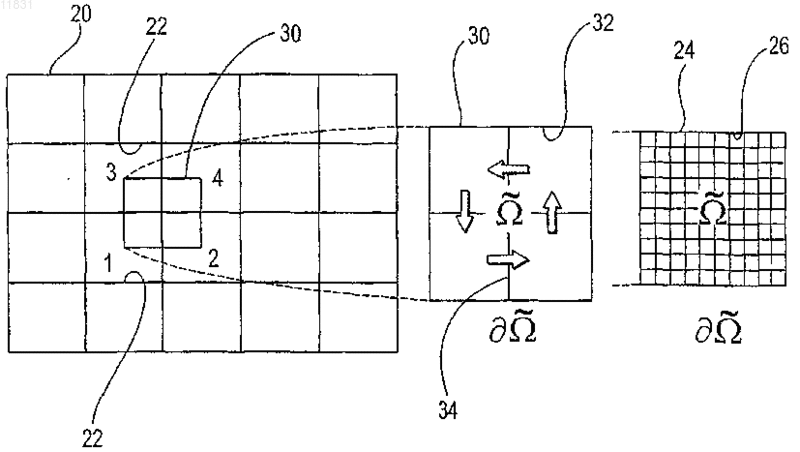
011831 Родственные заявки Заявка на данное изобретение представляет собой частично продолженную заявку для находящейся в процессе одновременного рассмотрения американской патентной заявки с серийным номером 10/383908, имеющей название Многомасштабный способ конечных объемов для использования при моделировании подземного течения, поданной 6 марта 2003 г., а также представляет собой частично продолженную заявку для находящейся в процессе одновременного рассмотрения заявки, имеющей название Многомасштабный способ конечных объемов для использования при моделировании подземного течения, поданной 22 сентября 2004 г., которая представляет собой продолжение находящейся в процессе одновременного рассмотрения американской патентной заявки с серийным номером 10/383908,имеющей название Многомасштабный способ конечных объемов для использования при моделировании подземного течения, поданной 6 марта 2003 г. Область техники, к которой относится изобретение Настоящее изобретение относится главным образом к симуляторам подземного пластового резервуара, а конкретнее, к таким симуляторам, в которых используется многомасштабная физика для моделирования потока в подземном пластовом резервуаре. Уровень техники изобретения Уровень детализации, подходящий для описания пластового резервуара, часто превышает вычислительные возможности существующих симуляторов пластового резервуара. Данный разрыв в осуществлении решения обычно преодолевают путем укрупнения масштаба точного отсчета для различных величин, которые можно обрабатывать с помощью полнофункционального симулятора. При масштабировании исходную модель огрубляют, используя экономный в вычислительном отношении процесс. В поточных методах процесс основан на однофазном потоке. Затем осуществляют исследование с помощью моделирования, используя огрубленную модель. Методы масштабирования, такие как эти, оказались вполне успешными. Однако при исследовании сложных потоковых процессов с использованием огрубленных моделей, сконструированных с помощью этих упрощенных установочных параметров, невозможно получить предварительную оценку имеющихся погрешностей. Для непосредственного использования описания мелкомасштабного точного отсчета были предложены различные фундаментальные многомасштабные приближения для потока в пористых средах. В противоположность увеличению масштаба многомасштабное приближение нацелено на оригинальное решение всей проблемы. Методология масштабирования обычно основана на создании представляющего интерес разрешения по длине и по временной шкале путем максимизации локальных операций. В работах Арбогаста и др. (Т. Arbogast, Численное масштабирование частичной решетки двухфазного потока в пористых средах, Технический отчет, Техасский институт вычислительной и прикладной математики,Техасский университет в Остине, 1999, и Т. Arbogast и S.L. Bryant, Численное масштабирование частичной решетки для моделирований обводнения, SPE (Общество инженеров-нефтяников) 66375, 2001) представлен смешанный способ конечных элементов, где мелкомасштабные элементы локализованы граничными допущениями на границах крупного элемента. Затем мелкомасштабное влияние связывают с крупномасштабными эффектами с помощью численных функций Грина. Т. Хоу и Х. By (T.Y. Hou и X.H. Wu,Многомасштабный способ конечных элементов для эллиптических задач в композитных материалах и пористых средах, Journal of Computational Physics (Журнал вычислительной физики), 134:169-189, 1997) использовали приближение конечных элементов и спроектировали конкретные базисные функции, в которые введены мелкие масштабы. В свою очередь, локализацию получают с помощью граничных допущений для крупных элементов. Для снижения влияний этих граничных условий можно применять технологию передискретизации. Чен и Хоу (Z. Chen и T.Y. Hou, Смешанный способ конечных элементов для эллиптических задач с быстро изменяющимися коэффициентами, Math. Comput (Прикладная математика и вычисления), июнь, 2002) использовали эти идеи в сочетании со смешанным приближением конечных элементов. Другое приближение, разработанное Бекки и др. (R. Beckie, A.A. Aldama и E.F.Wood, Моделирование крупномасштабной динамики насыщенного потока подземных вод с использованием пространственной фильтрации, Water Resources Research (Исследование водных ресурсов), 32:12691280, 1996), основано на технологиях моделирования крупных завихрений (large eddy simulation (LES,которые обычно используют для моделирования турбулентности. Ли и др. (S.H. Lee, L.J. Durlofsky, M.F. Lough и W.H. Chen, Способ конечных разностей геологически сложных пластовых резервуаров с тензорными проницаемостями, SPEREE, с. 567-574, 1998) разработали схему конечной разности непрерывного потока (FCFD) для двумерных моделей. Ли и др. дополнительно разработали способ, предназначенный для трехмерных моделей (S.H. Lee, H. Tchelepi, P. Jenny и L. Dechant, Внедрение способа конечной разности непрерывного потока для стратиграфических, гексаэдрических масштабных сеток, Журнал SPE (Общества инженеров-нефтяников), Сентябрь, с. 269-277,2002). Дженни и др. (P. Jenny, С. Wolfsteiner, S.H. Lee и L.J. Durlofsky, Моделирование потока в геометрически сложных пластовых резервуарах с использованием гексаэдрических мультиблочных сеток,Журнал SPE, Июнь, страницы 149-157, 2002) позднее внедрили эту схему в мультиблочный симулятор.-1 011831 В свете вышеупомянутых работ по моделированию существует необходимость в способе моделирования, в котором более эффективно учитываются влияния мелких масштабов на крупную сетку. В идеале, способ может быть консервативным, а также с помощью него можно корректно обрабатывать тензорные проницаемости. Кроме того, является предпочтительным, чтобы реконструированное мелкомасштабное решение соответствовало надлежащему балансу по массе в мелком масштабе. Настоящее изобретение обеспечивает такой способ моделирования. Сущность изобретения Многомасштабный способ конечных объемов (MSFV) освоен для решения эллиптических или параболических задач, таких как задачи, пригодные для симуляторов подземных потоков. Преимущества настоящего способа MSFV состоят в том, что он хорошо вписывается в рамки способа конечных объемов, предусматривает эффективную вычислительную обработку крупномасштабных проницаемостей,пригоден для надлежащей обработки тензорных проницаемостей и является консервативным как для крупного масштаба, так и для мелкого масштаба. Настоящий способ является вычислительно эффективным по сравнению с моделированием пластового резервуара, используемым в настоящее время, и он хорошо подходит для параллельной вычислительной обработки массива. Настоящее изобретение можно применять для трехмерных неструктурированных сеток, а также для многофазного потока. Кроме того,реконструированное мелкомасштабное решение соответствует надлежащему балансу по массе для мелкого масштаба. Описано многомасштабное приближение, которое приводит к появлению эффективных проницаемостей при решении крупномасштабной задачи. Как только проницаемости были созданы, в способеMSFV появилась возможность использования схемы конечных объемов, в которой применяются многоточечные шаблоны для дискретизации потока. Приближение является консервативным и с его помощью можно корректно обрабатывать тензорные проницаемости. Этот способ легко применяют, используя существующие стандарты методов конечных объемов, и для вычисления проницаемостей, способ, с вычислительной точки зрения, является очень эффективным. При вычислении эффективных проницаемостей используют допущение замыкания. Важная характеристика настоящего многомасштабного способа состоит в том, что в нем использованы два множества функций. Первое множество функций двойственного базиса рассчитывают для конструирования проницаемостей между крупномасштабными ячейками. Второе множество локально рассчитываемых мелкомасштабных базисных функций используют для реконструирования мелкомасштабного поля скоростей из крупномасштабного решения. Это второе множество мелкомасштабных базисных функций спроектировано таким образом, чтобы реконструированное мелкомасштабное поле скоростей было полностью совместимым с проницаемостями. Кроме того, данное решение соответствует надлежащему балансу масс для мелкого масштаба. Способ MSFV можно использовать для моделирования подземного пластового резервуара. Сначала создают мелкую расчетную сетку, создающую множество мелких ячеек. Поле проницаемости и другие мелкомасштабные свойства связаны с мелкими ячейками. Затем, создают крупномасштабную сетку, которая создает множество крупных ячеек, где между крупными ячейками существуют границы раздела. Крупные ячейки в идеале являются совокупностями мелких ячеек. Двойственную крупную сетку конструируют, создавая множество двойных крупных управляющих объемов. Двойные крупные управляющие объемы в идеале также представляют собой совокупности мелких ячеек. Двойные крупные управляющие объемы окружены границами. Затем по двойным крупным управляющим объемам рассчитывают функции двойственного базиса путем решения локальных эллиптических или параболических задач предпочтительно с использованием граничных условий, полученных из решения редуцированных задач вдоль границ раздела крупных ячеек. Потоки, предпочтительно интегральные потоки, затем извлекают через границы раздела двойных крупных ячеек из функций двойственного базиса. Эти потоки компонуют для получения эффективных проницаемостей между крупными ячейками расчетной сетки крупных ячеек. Проницаемости можно использовать для расчетов крупномасштабных конечных объемов. Можно создать мелкомасштабное поле скоростей. Способ конечных объемов используют для вычисления давления в крупных ячейках, в которых между ячейками использованы проницаемости. Мелкомасштабные базисные функции рассчитывают путем решения локальных эллиптических или параболических потоковых задач для крупных ячеек и путем использования мелкомасштабных потоков через границы раздела крупных ячеек, которые извлекают из функций двойственного базиса. Наконец, мелкомасштабные базисные функции и соответствующие давления в крупных ячейках комбинируют для извлечения мелкомасштабного поля скоростей. Задачу переноса можно решать на мелкой расчетной сетке с использованием мелкомасштабного поля скоростей. В идеале, задачу переноса решают итерационно в два этапа. На первом этапе мелкомасштабное поле скоростей получают из решения уравнения давлений. На втором этапе задачу переноса решают на мелких ячейках, используя мелкомасштабное поле скоростей. Для решения задачи переноса локально на каждой крупной ячейке можно применять технологию наложения Шварца с противопоточной схемой неявного решения.-2 011831 Решение, которое можно рассчитать на крупных ячейках при возрастающем времени и свойствах,таких как коэффициент передачи, можно создать для мелких ячеек при возрастающем времени. Затем,если заданные условия не установлены для всех мелких ячеек внутри двойного крупного управляющего объема, реконструируют функции двойственного базиса и мелкомасштабные базисные функции в этом двойственном крупном управляющем объеме. Краткое описание чертежей Эти и другие цели, отличительные признаки и преимущества настоящего изобретения станут лучше понятыми при рассмотрении следующего описания, находящейся на рассмотрении формулы изобретения и прилагаемых чертежей, где: фиг. 1 иллюстрирует крупную двумерную сетку крупных ячеек с наложенной на нее двойной крупной сеткой, включающей в себя двойной крупный управляющий объем и наложенную мелкую сетку,состоящую из мелких ячеек; фиг. 2 иллюстрирует крупную сетку, включающую в себя девять смежных крупных ячеек (жирные сплошные линии) с соответствующей наложенной двойной крупной сеткой (жирные пунктирные линии),включающую в себя двойные крупные управляющие объемы и наложенную мелкую сетку (тонкие точечные пунктирные линии) мелких ячеек; фиг. 3 показывает вклады потоков qA(2) и qB(2), вызванные давлением в конкретной крупной ячейке 2; фиг. 4 представляет собой блок-схему, описывающую все этапы, используемые в предпочтительном варианте воплощения моделирования пластового резервуара, в котором использован многомасштабный способ конечных объемов (MSFV), созданный в соответствии с данным изобретением; фиг. 5 представляет собой блок-схему, дополнительно детализирующую этапы, используемые для определения проницаемостей Т между крупными ячейками; Фиг. 6 представляет собой блок-схему, дополнительно описывающую этапы, используемые для проектирования множества мелкомасштабных базисных функций и для получения мелкомасштабного поля скоростей; фиг. 7 представляет собой блок-схему, описывающую связь между давлением и уравнениями насыщенности, в которых использована схема неявного решения и в которыхипредставляют собой операторы, используемые для обновления полной скорости и насыщенности соответственно, в ходе одного этапа времени; фиг. 8 представляет собой иллюстрацию использования адаптационной схемы для селективного обновления базисных функций; фиг. 9 представляет собой иллюстрацию поля проницаемости, связанного с задачей 10 SPE; фиг. 10 А, В представляют собой иллюстрации поля проницаемости верхнего слоя и нижнего слоя ячеек из задачи 10 SPE; фиг. 11 А, В представляют собой иллюстрации полей насыщенности слоев ячеек, созданных с использованием способа MSFV, а фиг. 11 С представляет собой иллюстрацию поля насыщенности, рассчитанного с помощью стандартного мелкомасштабного симулятора пластового резервуара; фиг. 12 А, В представляют собой иллюстрации полей насыщенности нижних слоев ячеек, созданных с использованием способа MSFV, а фиг. 12 С представляет собой иллюстрацию поля насыщенности, рассчитанного с помощью стандартного мелкомасштабного симулятора пластового резервуара; фиг. 13 А, В представляют собой графики разжижения нефти и регенерации нефти; фиг. 14 представляет собой иллюстрацию трехмерного контрольного примера, имеющего сетку 102217 ячеек сетки и включающего в себя нагнетающие и добывающие скважины; и фиг. 15 представляет собой кривые разжижения нефти и кривые нефтеотдачи. Наилучшие варианты осуществления изобретенияI. Потоковая задача. А. Однофазный поток. Поток флюида в пористых средах можно описать следующей эллиптической задачей: где р - давление;- коэффициент подвижности (проницаемость K, деленная на вязкость флюида );- объем или имитируемая область под поверхностью земли. Характеристика источника f представляет собой скважины, а в случае сжатия - производные по времени. Неоднородность по проницаемости - это определяющий фактор при определении поведения потока в естественных пористых породах. Неоднородность по проницаемости K обычно представлена в виде сложной многомасштабной функции пространства. Более того, проницаемость K имеет тенденцию к тому, чтобы представлять собой высокодискретный полный тензор. Для решения задач пространственных корреляционных структур и ввода переменной для проницаемости требуется очень подробное описание пластового резервуара.-3 011831 Скорость потока флюида u связана с полем давления через закон Дарси На границе объемауказан поток q=u, где- граничный единичный вектор нормали, направленный наружу. Уравнения (1) и (2) описывают несжимаемый поток в пористой среде. Эти уравнения применяют как для однофазных, так и для многофазных потоков при соответствующих интерпретациях коэффициента подвижностии скорости u. Данная эллиптическая задача является простым, к тому же характерным описанием типа систем, которые можно эффективно рассчитывать с помощью симулятора подземного потока. Более того, пригодность данного предельного случая несжимаемого потока для расчета обеспечивает возможность обработки сжимаемых систем в качестве подмножества. В. Двухфазный поток. Поток двух несжимаемых фаз в гетерогенной области можно математически описать следующими формулами:kr0,w - относительные проницаемости (которые представляют собой функции S0,w);q0,w - характеристики источников, которые характеризуют скважины. Предполагается, что капиллярное давление и плотность системы незначительны. Эквивалентно,систему (3) можно описать как по объемус а общую подвижность можно описать как где kj=krj/j для j0,w. Уравнение (4) известно как уравнение давления, а уравнение (5) - как гиперболическое уравнение переноса. И в этом случае уравнения (4) и (5) представляют собой характерное описание типа систем, которые подлежат эффективному обсчету с помощью симулятора подземного потока. Такие симуляторы потоков, а также технологии, используемые для моделирования потока, хорошо известны специалистам в данной области техники и описаны в таких публикациях, как Моделирование нефтяного пласта, K. Aziz и A. Settari, Stanford Bookstore Custom Publishing, 1999.II. Многомасштабный способ конечных объемов (MSFV). А. Способ MSFV для однофазного потока. 1. Способ конечных объемов. Далее будет описан способ конечных объемов при центрированной ячейке. Для решения задачи,описываемой уравнением (1), общий объем или объемразделяют на меньшие объемы Решение конечных объемов, таким образом, удовлетворяет уравнению для каждого управляющего объема нормали границы объема ,где- единичный вектор нормали границы объема, направленный наружу. Задача состоит в поиске достаточно хорошего приближения для при в объемах области . ОбУравнение (9) является линейной комбинацией величин давленияk щее количество объемов составляет n, a T означает коэффициент передачи между объемами. По определению, потоки из уравнения (9) являются непрерывными в направлении через границы разделов объемов, и в итоге способ конечных объемов является консервативным. 2. Построение эффективных коэффициентов передачи. Способ MSFV приводит к созданию многоточечных шаблонов для крупномасштабных потоков. Для следующего описания используют ортогональную двумерную сетку 20 из ячеек 22 сетки, как показано на фиг. 1. Наложенная мелкомасштабная сетка 24 из ячеек 26 мелкомасштабной сетки содержит информацию K о мелкомасштабной проницаемости. Для вычисления коэффициентов передачи Т между крупными 22 ячейками сетки используют двойственную 30 крупную сетку из двойных крупных 32 управляющих объемов. Управляющий объем 32 двойной сетки 30, , создают путем соединения средних точек четырех смежных ячеек 22 крупной сетки. Для соотнесения потоков через границы раздела 34 ячеек крупной сетки, которые находятся внутри конкретного управляющего объема 32, или , с давлениями в четырех смежных ячейках 22 крупной сетки локальную эллиптичев конечных объемах скую задачу в предпочтительном варианте воплощения задают следующим образом: Для специалистов в данной области техники должно быть понятно, что способ легко можно приспособить для использования в локальной параболической задаче. должны быть указаны граничные условия Дирихле или Для эллиптической задачи на границе Неймана. В идеале, наложенные граничные условия должны быть приближенными к настоящим условиям потока, которым подвергается подобласть в общей системе. Эти граничные условия могут зависеть от времени и от потока. Поскольку подобласть встроена во всю систему, Wallstrom и др. (Т.С. Wallstrom,T.Y. Hou, M.A. Christie, L.J. Durlofsky и D.H. Sharp Применение новой двухфазной технологии увеличения масштаба к реальным поперечным сечениям пластовых резервуаров, SPE 51939, представленное на симпозиуме SPE по моделированию пластовых резервуаров, Хьюстон, 1999) обнаружили, что условия постоянного давления на границе подобласти способствуют переоценке вкладов потоков из проницаемых областей. Если корреляционная длина проницаемости не намного больше, чем этап сетки, вклад потока из областей с высокой проницаемостью не пропорционален номинальному коэффициенту проницаемости. Коэффициент передачи между двумя ячейками представляет собой среднее гармоническое,которое близко к наинизшей проницаемости. В результате однородные условия потока вдоль границы часто приводят к лучшим численным результатам для задачи подобласти, чем линейные или постоянные условия давления. Т. Хоу и Х. Ву (T.Y. Hou и X.H. Wu, Многомасштабный способ конечных элементов для эллиптических задач в композитных материалах и пористых средах, Журнал вычислительной физики, 134:169189, 1997) также предлагают решение редуцированной задачи для определения граничных условий для локальной задачи. Подстрочный индекс t означает компонент, параллельный границе двойного крупного 32 управ. ляющего объема, или Для уравнения (11) и для следующей части данного технического описания будет использовано эйнштейновское обозначение суммирования. Эллиптическую задачу для управляющего объема с граничными условиями уравнения (11) для можно решать с помощью любого подходящего численного способа. Для получения решения задачи, в данном предпочтительном варианте водавления, которое линейно зависит от давлений площения решаются эллиптические задачи: одна на каждое давление в центре ячейки. Например, для получения решения задачи давления в ячейке крупной сетки, имеющей узел 1 в ее центре, задают. в управляющем объеме Четыре решения обеспечивают функции двойственного базиса, а решение задачи давления в локальной эллиптической задаче в управляющем объеме представляет собой линейную комбинацию-5 011831 Следовательно, поток q через границы ячеек сетки можно записать в виде линейной комбинации где qk (k=1,4) представляют собой комбинации потоков из соответствующих функций двойственного базиса, все из которых выведены из управляющих объемов . Вычисляют эффективные коэффициенты передачи Т, которые можно использовать для моделирований конечных объемов, собирая воедино вклады потоков, в предпочтительном варианте воплощения вклады интегральных потоков через границы 34 ячеек. Следует отметить, что область может обладать любым мелкомасштабным распределением коэффициентов подвижности X. Разумеется, граничные условия, заданные уравнением (11), являются приближением, которое позволяет решать с его помощью локальные задачи. Решения с помощью способаMSFV и глобальные мелкомасштабные решения идентичны только в случае, если уравнение (11) используется для введения точного решения мелкомасштабного решения задачи давления. Тем не менее, проведенные численные эксперименты показывают, что уравнение (11) является отличным приближением для граничного условия. Хотя приближение MSFV является способом конечных объемов, оно похоже на многомасштабный способ конечных объемов Wu и Hou, кратко описанный выше. Структура их функций двойственного базиса аналогична, хотя в настоящем способе MSFV они представлены на двойной крупной сетке, а не на границе конечного элемента. Существенное различие состоит в том, что настоящий способ MSFV представляет собой способ конечных объемов с центрированными ячейками и является консервативным. С другой стороны, матрица масс в многомасштабном способе конечных элементов создана на основе вариационного принципа и не обеспечивает локального сохранения. В следующем разделе показана важность мелкомасштабного поля скоростей, которое является консервативным. 3. Реконструирование консервативного мелкомасштабного поля скоростей. Потоки через границы 34 крупных ячеек можно точно рассчитывать с помощью многомасштабных коэффициентов проницаемостей T. В некоторых случаях представляет интерес точное отображение мелкомасштабных скоростей u (например, прогнозирование распределения растворенного вещества, транспортируемого флюидом). Для использования функций двойственного базиса уравнения (12) можно воспользоваться приближением движения прямо и вперед. Однако далее реконструированное мелкомасштабное поле скоростей является в основном дискретным на границах ячеек двойной сетки 30. Поэтому в дивергентном поле могут возникнуть крупные погрешности, а локальный баланс масс нарушается. Следует отметить, что требование сохранения массы всегда удовлетворяется для раствора, для которого используется настоящий способ MSFV. Далее будет описано построение второго множества локальных мелкомасштабных базисных функций , которое полностью соответствует потокам q через границы ячеек, заданные функциями двойственного базиса . Это второе множество мелкомасштабных базисных функцийпозволяет реконструировать консервативное мелкомасштабное поле скоростей. На фиг. 2 показана крупная сетка 20 с девятью смежными ячейками 22 сетки и соответствующая двойная сетка 30 двойных крупных управляющих объемов 32 или . В целях индексирования эти конкретные ячейки и соответствующие двойные объемы далее следует пометить цифрами 1-9 и буквами A-D в их соответствующих центрах. Также показана наложенная мелкая 24 сетка, состоящая из элементов 26 крупной сетки. Крупная сетка, имеющая девять смежных крупных ячеек 1-9, показана жирными сплошными линиями. Соответствующая двойная сетка 30 двойных крупных управляющих объемов A-D обозначена жирными пунктирными линиями. Наложенная мелкая 24 сетка, состоящая из ячеек 26 мелкой сетки, показана в виде тонких точечных пунктирных линий. Для объяснения реконструирования мелкомасштабного поля скоростей был рассмотрен баланс масс в центре ячейки 5 сетки. Решение крупномасштабной задачи давления, наряду с функциями двойственного базиса , обеспечивает мелкомасштабные потоки q через границы крупной ячейки 5. Для получения надлежащего отображения мелкомасштабного поля скоростей в крупной ячейке 5(i) мелкомасштабные потоки через границу крупной ячейки 5 должны быть согласованы, a (ii) дивергенция мелкомасштабного поля скоростей в крупном объеме должна удовлетворять уравнению- ячейка 5 крупной сетки. Мелкомасштабный поток q через границу ячейки 5 сетки зависит от решения крупномасштабной задачи давления в ячейках 1-9 сетки. Поэтому мелкомасштабное поле скоростей в крупной ячейке 5 сетки можно выразить в виде суперпозиции мелкомасштабных базисных функций i (i=1,9). С помощью фиг. 3, на которой изображены необходимые двойные крупные управляющие объемы, будут описаны где-6 011831 построение необходимых мелкомасштабных двойных крупных управляющих объемов и построение мелкого масштаба при построении мелкомасштабных базисных функций i. Каждое давление в крупной ячейке вносит вклад в мелкомасштабный поток q. Например, положим вклад давления в ячейке 2 в поток q в ячейке 5 сетки равным q(2). Следует отметить, что q(2) состоит из вкладов qA(2) и qB(2), происходящих из функций двойственного базиса, связанных, соответственно, с узлом 2 объема А и объема В. Для вычисления мелкомасштабной базисной функции i, связанной с давлением в крупной ячейке i, устанавливают, а поле давления создают согласно следующему уравнению: Мелкомасштабные потоки q рассчитывают из поля давления. Эти потоки обеспечивают надлежащие граничные условия для расчета мелкомасштабной базисной функции i. Для решения эллиптической задачи с граничными условиями, описанными выше, должна быть обеспечена растворимость. Это достигается уравнением которое представляет собой характеристику равномерно распределенного источника в. Наконец, решение эллиптической задачи (16) и (17) представляет собой мелкомасштабную базисную функцию i для крупной ячейки 5, связанной с давлением в объеме i. Крупномасштабное поле скоростей выводят из суперпозиции Для несжимаемого потока в данном поле скоростей дивергенция отсутствует везде. Расчет мелкомасштабных базисных функций i требует решения девяти малых эллиптических задач, которые характеризуются тем же размером, что и задачи для вычислений коэффициента передачи. Следует отметить,что этот этап является этапом подготовительной обработки и должен быть сделан только один раз. Кроме того, построение мелкомасштабных базисных функций i является независимым и поэтому хорошо подходит для параллельного вычисления. Реконструирование мелкомасштабного поля скоростей представляет собой простую суперпозицию, и в идеале ее выполняют только в областях, представляющих интерес. В качестве альтернативы консервативное мелкомасштабное поле скоростей можно также конструировать непосредственно на месте. Данное конструирование можно осуществлять следующим образом:(i) рассчитывать мелкомасштабные потоки через границы крупных ячеек, используя функции двойственного базиса с давлениями для крупных ячеек;(ii) решать уравнение для давления по каждой из крупных ячеек, используя мелкомасштабные потоки, рассчитанные на шаге (i) в качестве граничных условий для получения мелкомасштабных давлений;(iii) рассчитывать мелкомасштабное поле скоростей из закона Дарси с использованием мелкомасштабных давлений, полученных на шаге (ii) с наложением мелкомасштабной проницаемости. Для системы с большой опорной поверхностью можно осуществлять решение уравнения давления на этапе (ii), например, путем повышенной дискретизации вокруг крупной ячейки.III. Реализация способа MSFV. Фиг. 4 представляет собой блок-схему, подводящую итоги шагам, используемым в предпочтительных вариантах воплощения при имитировании пластового резервуара с использованием алгоритмаMSFV согласно данному изобретению. Алгоритм MSFV состоит из шести главных этапов:A. Расчет коэффициентов передачи Т для крупномасштабных потоков (этап 100).B. Конструирование мелкомасштабных базисных функций (этап 200).C. Расчет крупномасштабного решения при новом временном уровне (этап 300).D. Реконструирование мелкомасштабного поля скоростей в областях, представляющих интересE. Решение уравнений переноса (этап 500).F. Пересчет коэффициентов передачи, а также мелкомасштабных базисных функций в областях, где общая подвижность изменилась более чем на заданную величину (этап 600). Этапы A-D описывают двухмасштабное приближение. Данную методологию можно применять рекурсивно с последующими уровнями укрупнения. В случаях крайне высокого разрешения данное многоуровневое решение должно приводить к масштабируемым решениям. Части Е и F отвечают за перенос, а подвижность изменяется из-за изменяющихся фаз и будет более подробно описана ниже.-7 011831 А. Расчет коэффициентов передачи для крупномасштабных потоков - этап 100. Расчеты коэффициента передачи можно сделать в автономном модуле (Т-модуле), и они хорошо подходят для параллельного расчета. Коэффициенты передачи Т можно вписывать в файл для использования в любом симуляторе конечного объема, который может функционировать на основе способа многоточечной дискретизации. Обращаясь теперь к фиг. 5, рассмотрим блок-схему, которая описывает индивидуальные этапы,предпринимаемые для расчета коэффициентов передачи Т для крупномасштабной модели. Сначала создают мелкомасштабную сетку, обладающую мелкими ячейками с соответствующим полем проницаемости K (этап 110). Затем создают крупную сетку, обладающую крупными ячейками, соответствующими мелкомасштабной сетке (этап 120). Мелкие и крупные сетки затем преобразуют в коэффициент передачи или Т-модуль. Создают двойные крупные управляющие объемы (этап 130), один на каждый узел крупной сетки. Для каждого крупного двойного управляющего объема создают функции двойственного базиса или крупномасштабные базисные функции CS (этап 140) путем решения локальных эллиптических задач(уравнение (10 для каждого объема . Используют данную локальную эллиптическую задачу, как описано в разделе II.А.2 выше, и поле проницаемости K, связанное с мелкой сеткой, а при решении эллиптической задачи используют граничные условия, соответствующие уравнению (11) (этап 135). В случае, если мелкие и крупные сетки несовместимы (например, если используются неструктурированные сетки), можно применять дискретизацию с повышенной частотой. Наконец, интегральные крупномасштабные потоки q через границы крупных ячеек выводят (этап 150) из функций двойственного базиса . Эти интегральные крупномасштабные базисные потоки q затем объединяют (этап 160) для получения MSFV-коэффициентов передачи Т между ячейками крупной сетки. Расчет коэффициентов передачи Т можно рассматривать в качестве процедуры увеличения масштаба. Т.е. созданные крупномасштабные решения задачи давления проектируют для принятия во внимание,в некоторой степени, мелкомасштабного описания проницаемости K в исходной мелкомасштабной модели сетки. Таким образом, часть А - этап 100 - вычисление коэффициентов передачи предпочтительно представляет собой отдельный этап предварительной обработки, используемый для укрупнения исходной мелкомасштабной модели до размера, поддающегося управлению в стандартном симуляторе пластового резервуара. Эти коэффициенты передачи Т можно вписать в файл для дальнейшего использования. В симуляторе конечного объема, который может функционировать на основе способа многоточечной дискретизации, можно затем использовать эти коэффициенты передачи Т. В. Построение мелкомасштабной базисной функции и мелкомасштабного поля скоростей - этап 200. Фиг. 6 представляет собой блок-схему, описывающую этапы, используемые для конструирования мелкомасштабных базисных функций , которые можно выделить в отдельный модуль мелкомасштабных базисных функций . Эти мелкомасштабные базисные функцииможно затем использовать для создания мелкомасштабного поля скоростей. Этот модуль необходим только в случае, если он представляет интерес для реконструирования мелкомасштабного поля скоростей из крупномасштабного решения задачи давления. Как описано выше в разделе II.A.3, при использовании исходных функций двойственного базиса для реконструирования мелкомасштабного поля скоростей может произойти крупная ошибка баланса масс. Здесь описаны этапы для вычисления мелкомасштабных базисных функций ,которые можно использовать для реконструирования консервативного мелкомасштабного поля скоростей. Данная процедура (этап 200) фиг. 4 следует описанию, приведенному в разделе II.А.3, и должна быть осуществлена только один раз, в начале моделирования, и она хорошо подходит для параллельного вычисления. Мелкомасштабную сетку (этап 210) с ее соответствующим полем проницаемости K, крупную сетку(этап 230) превращают в мелкомасштабную базисную функцию . Поле давления создают из крупномасштабного решения задачи давления и функций двойственного базиса (этап 250). Затем проводят расчет мелкомасштабных потоков для крупных ячеек (этап 260). Для определения мелкомасштабных базисных функций (этап 270) для каждого рабочего объема решают эллиптические задачи, используя мелкомасштабные потоки в качестве граничных условий. Мелкомасштабное поле скоростей можно затем вычислять из суперпозиций давлений ячейки и мелкомасштабных базисных функций. Результаты можно затем выводить из модуля. В качестве альтернативы мелкомасштабное поле скоростей можно вычислять непосредственно на месте, как было описано выше в разделе II.A.3. Во многих случаях мелкомасштабное поле скоростей необходимо реконструировать только в некоторых областях, как будет более подробно описано ниже. Поэтому для сохранения памяти и времени вычисления можно подумать над непосредственным расчетом мелкомасштабных базисных функций , которые после их расчета можно использовать многократно.C. Расчет крупномасштабного решения в новое время - этап 300. Этап 300 можно осуществлять путем любого виртуального многоточечного шаблонного способа конечных объемов с помощью использования MSFV-коэффициентов передачи Т для вычисления потоков. В эти крупные потоки эффективно вводят крупномасштабные характеристики решения без разрешения в мелком масштабе.D. Реконструирование мелкомасштабного поля скоростей - этап 400. Этап 400 является прямым. Реконструирование мелкомасштабного поля скоростей в областях,представляющих интерес, достигают путем наложения мелкомасштабной базисной функции, как показано на фиг. 6. В качестве альтернативы мелкомасштабное поле скоростей можно непосредственно вычислять из функций i, как описано в разделе II.А.3, этап В. Разумеется, можно разрабатывать много вариантов способа MSFV. Он может быть очень эффективным; однако такое конструирование проницаемостей Т и мелкомасштабных функцийможно осуществлять в виде модулей, отделенных от модулятора. Е. Решение уравнений давления и уравнений переноса. 1. Алгоритм численного решения - решение в явном виде. Многофазные задачи о потоках можно решать в две стадии. Сначала общее поле скоростей получают из решения уравнения (4) давлений, а затем решают гиперболическое уравнение (5) переноса. Для решения уравнения давлений используют способ MSFV, который был описан выше. Отличие от однофазного потока состоит в том, что в данном случае термин подвижностьотражает общую подвижность в обеих фазах, и, кроме того, полученное поле скоростей и представляет собой полную скорость в области. Реконструированное мелкомасштабное поле скоростей u затем используют для решения уравнения переноса для мелкой сетки. Значения k0,w берут из направления вверх по потоку; интегрирование по времени можно получать, используя обратную схему Эйлера. Следует отметить, что обычно функции двойственного базиса и мелкомасштабные базисные функции необходимо вычислять заново на каждом временном этапе из-за изменений в поле насыщенности (подвижности). 2. Алгоритм численного решения - неявная связь. В предпочтительном варианте воплощения данного изобретения в способе MSFV использован алгоритм с неявными вычислениями. Многофазную потоковую задачу решают итерационно в две стадии. Рассмотрим фиг. 7 для диаграммы по данному методу, иллюстрирующий связь между давлением и уравнениями насыщенности. Сначала на каждом шаге по методу Ньютона устанавливают поле насыщенности S либо путем исходного ввода, либо через итерацию (этап 510). Затем решают уравнение давления (уравнение (19, этап 520, используя технологии MSFV, описанные выше, для получения (этап 530) полного поля скоростей. Затем решают уравнение переноса (уравнение (20, этап 540, для тонкой сетки с использованием реконструированного мелкомасштабного поля скоростей u. В данном решении применена технология наложения Шварца, т.е. проблему переноса решают локально для каждого крупного объема с неявной противопоточной схемой, где для граничных условий используют значения насыщенности из соседних крупных объемов при предыдущем уровне итерации. После схождения схемы наложения Шварца (этапы 550, 560) для гиперболической системы данный способ становится очень эффективным - новое распределение насыщенности определяет новое общее поле подвижности для задачи давления из следующей итерации Ньютона. Следует отметить, что, как правило, некоторые из базисных функций приходится пересчитывать при каждой итерации. Верхние индексы n иозначают, соответственно, предыдущее время и уровни итерации. Насыщение представлено S, общее поле скоростей - u, вычисление скорости - оператором , а вычисление насыщенности - . Новое поле давления p+1 получают решением из которого рассчитывают новое поле скоростей u+1. Новое поле насыщенности S+1 получают решением уравненияF. Повторный расчет коэффициентов передачи и мелкомасштабных базисных функций - адаптивная схема/ Наиболее ценная часть алгоритма MSFV для многофазного потока состоит в реконструировании. крупномасштабных и мелкомасштабных базисных функций Поэтому для получения повышенной эффективности является желательным осуществлять повторный расчет базисных функций только тогда, когда это абсолютно необходимо. Для усовершенствования этих базисных функций можно использовать адаптивную схему. В предпочтительном образцовом варианте воплощения, если условие не выполняется (надстрочные индексы n и n-1 означают два предыдущих временных этапа, a- заданное значение) для всех мелких ячеек внутри крупного объема, то функции двойственного базиса, которые управляют объемом, следует реконструировать. Следует отметить, что условие (23) истинно, если А изменяется на величину, которая больше 1/(1+) и меньше 1+. Иллюстрация данной схемы показана на фиг. 8, где крупные и мелкие ячейки сетки вычерчены, соответственно, тонкими и жирными линиями. Черные квадраты представляют мелкие ячейки, в которых условие (23) не выполняется. Квадраты с жирными пунктирными линиями представляют собой управляющие объемы, для которых функции двойственного базиса следует реконструировать. Заштрихованные области представляют крупные ячейки, для которых мелкомасштабные базисные функции следует обновить. В схематичном двумерном примере из фиг. 8 должны быть реконструированы только 20 из 196 всюду определенных базисных функций и 117 из 324 всюду определенных мелкомасштабных базисных функций. Конечно, эти величины сильно зависят от заданного порогового значения . Обычно меньшее пороговое значение вызывают более мелкие объемы и, в результате, необходимость в пересчете большего количества базисных функций на каждом временном этапе. Для широкого разнообразия контрольных случаев было обнаружено, что принятиеравным 0,2 приводит к незначительным изменениям в полученных результатах.IV. Численные результаты. Данный способ MSFV в сочетании со схемой неявной связи, показанной на фиг. 7, был протестирован на двухфазный поток (0/w10) в жесткой трехмерной модели с более 140000 мелких клеток. Было продемонстрировано, что многомасштабные результаты отлично согласуются с мелкомасштабным решением. Более того, способ MSFV оказался приблизительно в 27 раз более эффективным, чем стандартный симулятор нефтяного пластового резервуара Чиарса. Однако во многих случаях эффективность вычислений оказалась спорной из-за ограничений по величине временного этапа, присущего для схемIMPES. Данную проблему можно решить применением полностью неявного способа MSFV, который был описан в предыдущем разделе. Здесь численные исследования показывают следующее.(1) Результаты, полученные с помощью неявного способа MSFV, отлично согласуются с мелкомасштабными результатами.(2) Результаты, полученные с помощью неявного способа MSFV, не очень чувствительны к выбору крупной сетки.(3) Неявный способ MSFV для двухфазного потока компенсирует ограничения по величине временного этапа, и поэтому можно применять очень большие временные этапы.(4) Результаты, полученные с помощью неявного способа MSFV, являются в значительной степени интенсивными для величины временного этапа.(5) Неявный способ MSFV является очень эффективным. Для мелкомасштабного прогона сравнения был использован стандартный симулятор нефтяного пластового резервуара Чиарса. Эффективность как неявного способа MSFV, так и мелкомасштабного симулятора пластового резервуара зависит от выбора различных установок параметров, которые не были полностью оптимизированы. А. Контрольный пример. Были использованы исследования точности и эффективности полностью неявного алгоритмаMSFV, двумерные и трехмерные контрольные примеры с равномерно размещенными ортогональными сетками размером 6022060 и 22085. Трехмерная сетка и поле проницаемости были теми же самыми,что и для контрольного примера SPE 10, который рассматривают как крайне трудный для симуляторов пластового резервуара. Тогда как данный трехмерный контрольный пример используют для оценки эффективности вычислений, двумерный контрольный пример, который состоит из верхнего и нижнего слоев, служит для исследования точности способа MSFV. Фиг. 9 иллюстрирует трехмерный контрольный пример, заданный полем проницаемости задачи SPE 10. Более темные области означают более низкую проницаемость. Нагнетающую скважину помещают в центр поля, а четыре добывающие скважины - по углам. Эти расположения скважин используют для всех последующих исследований. Резервуар исходно заполняют нефтью, а /w=10 и kr0,w=S20,w. В. Двухмерное моделирование верхнего и нижнего слоев. В симуляторе MSFV использована недостающая в других методах усовершенствованная модель скважины. Т.е. скважины моделируют, задавая полные скорости для каждого перфорированного крупного объема. Поэтому для придания точности сравнениям между результатами MSFV и мелкомасштабными результатами (симулятор резервуара Чиарса) каждый мелкомасштабный объем внутри каждого перфорированного крупного объема представляет собой скважину при эксплуатации симулятора резервуара Чиарса. Для крупных трехмерных моделей это создает технические проблемы, поскольку симулятор пластового резервуара Чиарса не спроектирован для управления произвольно большим количеством отдель- 10011831 ных скважин. По этой причине было решено сделать точную оценку в двумерной модели, т.е. в верхнем и нижнем слоях трехмерной модели. Эти два слоя, для которых поля проницаемости показаны на фиг. 10 А и 10 В, являются репрезентативными для двух характеристически различных областей общей модели. Моделирования MSFV были осуществлены с помощью равномерно расположенных крупных сеток 1022 и 2044. Результаты были сопоставимы с мелкомасштабным решением для сетки 60220. Как и в полном трехмерном контрольном примере, четыре добывающие скважины установлены по углам, которые распределены по площади 610 мелкомасштабных ячеек. Нагнетающие скважины расположены в центрах областей и распределены по площади 1212 мелкомасштабных ячеек. Темпы работы скважин были одинаковыми для всех мелкомасштабных объемов (положительными для добывающих объемов и отрицательными для нагнетающих объемов). На фиг. 11 А-С и 12 А-С показаны поля проницаемости, соответственно, верхнего и нижнего слоев. Черные пятна означают зоны низкой проницаемости. Эти два слоя представляют две характеристически различные области общей трехмерной модели. На фиг. 11 А-С и 12 А-С показаны рассчитанные поля насыщенности после 0,0933 PVI (закачанный объем пор), соответственно, для верхнего и нижнего слоев. Тогда как на фиг. 11 С и 12 С показаны мелкомасштабные контрольные решения, на фиг. 11 А и 11 В и 12 А и 12 В показаны результаты MSFV для крупных сеток, соответственно, 1022 и 2044. Для обоих слоев можно наблюдать, что была достигнута отличная сходимость результатов и что многомасштабный способ вряд ли является чувствительным к выбору крупной сетки. Более качественное сравнение показано на фиг. 13 А и 13 В, где изображены мелкомасштабные и многомасштабные кривые разжижения нефти и нефтеотдачи. Принимая во внимание сложность этих тестовых задач и тот факт, что в целях сравнения используют два независимо друг от друга введенных в эксплуатацию симулятора, эту сходимость можно считать достаточно хорошей. В последующих исследованиях будет продемонстрировано, что для модели с 1122000 ячейками способ MSFV является существенно более эффективным, чем мелкомасштабные моделирования, а результаты остаются точными для очень больших этапов времени. С. Трехмерные моделирования. Тогда как двумерные исследования присущи исследованию точности неявного способа MSFV,крупные и сложные трехмерные вычисления требуются для оценки выразительной оценки эффективности. Трехмерный контрольный пример был использован, как описано выше. Была использована крупная сетка 102217, показанная на фиг. 14, и было закачано 0,5 объема пор. В противоположность методуMSFV скважины для моделирований по Чиарсу были установлены в соответствии с мелким масштабом. В таблице показано время счета центрального процессора и требуемое количество временных этапов для моделирования по Чиарсу и двух запусков способа MSFV. Сопоставление эффективности способа MSFV и мелкомасштабных моделирований Поскольку в способе Чиарса использовали алгоритм управления, величина временного этапа в многомасштабных моделированиях была постоянной. Это связано с величиной и сложностью задачи, в которой для успешного моделирования по Чиарсу приходится применять значительно меньшие временные этапы. В таблице показано, что с помощью неявного способа MSFV можно рассчитывать решение приблизительно в 27 раз быстрее, чем с помощью способа Чиарса. На фиг. 15 показаны кривые разжижения нефти и кривые нефтеотдачи, полученные с помощью многомасштабных моделирований с использованием 50 и 200 временных этапов. Хорошее совпадение между результатами подтверждает, что способ является очень устойчивым, что касается величины временного этапа. Поскольку стоимость моделирования MSFV почти линейно зависит от размера задачи и поскольку двойственную и мелкомасштабную базисную функцию можно рассчитать независимо, данный способ идеально подходит для массивных параллельных вычислений и решения огромных проблем. Несмотря на то что данное изобретение было описано, исходя из его определенных предпочтительных вариантов воплощения и многие детали были изложены в целях иллюстрации, специалистам в данной области техники должно быть ясно, что изобретение может быть подвержено изменениям и что некоторые другие детали, описанные в нем, могут значительно разниться, без отступления от основных принципов изобретения.- 11011831 ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Многомасштабный способ конечных объемов для использования при моделировании подземного пластового резервуара, содержащий этапы, на которых:(a) создают мелкую сетку, задающую множество мелких ячеек и имеющую поле проницаемости,связанное с мелкими ячейками;(b) создают крупную сетку, задающую множество крупных ячеек, имеющих границы раздела между крупными ячейками, причем крупные ячейки представляют собой совокупности мелких ячеек;(c) создают двойные крупные сетки, задающие множество двойных крупных управляющих объемов, причем двойные крупные управляющие объемы представляют собой совокупности мелких ячеек и имеют границы, ограничивающие двойные крупные управляющие объемы;(d) рассчитывают функции двойственного базиса по двойным крупным управляющим объемам путем решения локальных эллиптических или параболических задач;(e) выводят потоки через границы раздела крупных ячеек посредством функций двойственного базиса;(f) собирают воедино потоки для вычисления эффективных коэффициентов передачи между крупными ячейками;(g) рассчитывают давление в крупных ячейках с помощью способа конечных объемов и используя эффективные коэффициенты передачи между крупными ячейками и(h) рассчитывают мелкомасштабное поле скоростей. 2. Способ по п.1, в котором мелкомасштабное поле скоростей рассчитывают непосредственно на месте. 3. Способ по п.2, в котором этап расчета мелкомасштабного поля скоростей непосредственно на месте включает в себя этапы, на которых:(i) рассчитывают мелкомасштабные потоки через границы раздела крупных ячеек с использованием функций двойственного базиса с давлениями в крупных ячейках;(ii) решают уравнения давления для каждой из крупных ячеек с использованием мелкомасштабных потоков, рассчитанных при выполнении этапа (i) в качестве граничных условий для получения мелкомасштабных давлений и(iii) рассчитывают мелкомасштабное поле скоростей из закона Дарси с использованием мелкомасштабного давления, полученного при выполнении этапа (ii). 4. Способ по п.3, в котором решение уравнения давления на этапе (ii) для получения мелкомасштабных давлений выполняют для системы с большой опорной поверхностью. 5. Способ по п.4, в котором решение уравнения давления на этапе (ii) можно выполнять путем передискретизации вокруг крупных ячеек. 6. Способ по п.3, в котором решение уравнения давления на этапе (ii) можно выполнять путем передискретизации вокруг крупных ячеек.