Способ и компьютерный носитель информации для анализа характеристик подземной формации
Формула / Реферат
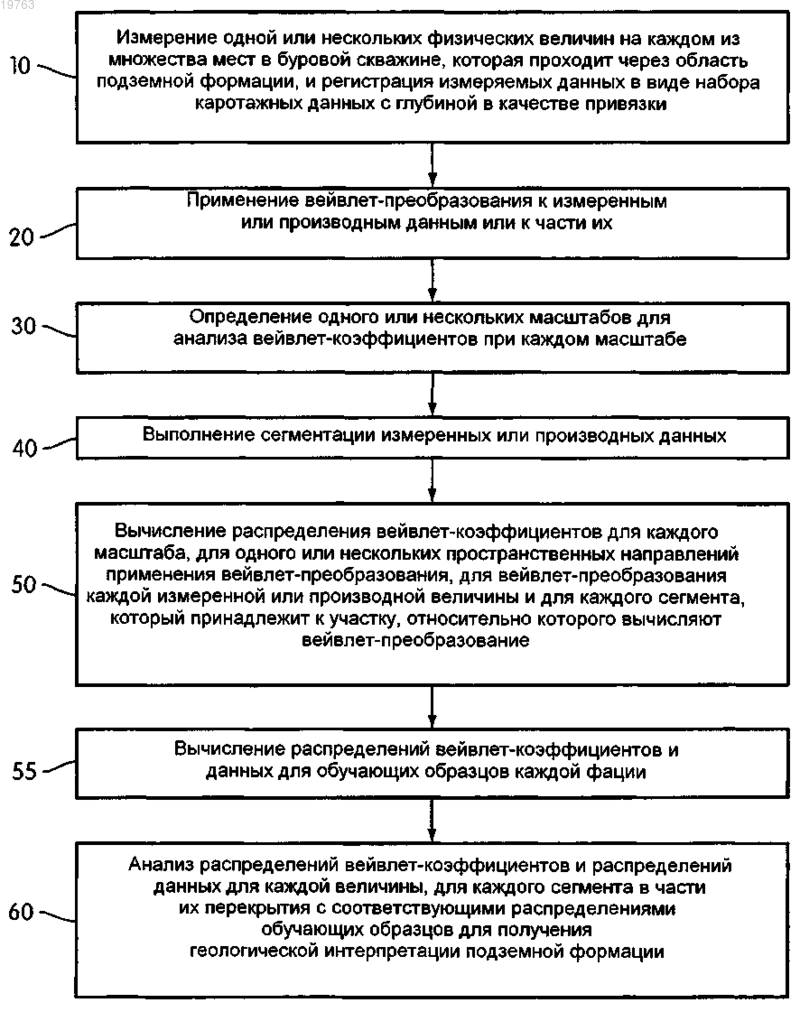
1. Реализуемый с помощью компьютера способ анализа характеристик подземной формации, содержащий этапы, на которых
применяют посредством процессора компьютера вейвлет-преобразование к измеренным данным или к производным данным, полученным на основании измеренных данных, или к части их, при этом измеренные данные получены измерением по меньшей мере одного физического параметра на каждом из множества мест в буровой скважине, которая проходит через область подземной формации;
выбирают один или несколько масштабов для анализа вейвлет-коэффициентов при каждом масштабе;
выполняют сегментацию измеренных или производных данных;
вычисляют посредством процессора компьютера распределение вейвлет-коэффициентов для каждого масштаба для одного или нескольких пространственных направлений применения вейвлет-преобразования, для вейвлет-преобразования измеренных или производных данных и для каждого сегмента, который принадлежит к участку, относительно которого было вычислено вейвлет-преобразование;
для каждого сегмента анализируют распределение измеренных или производных данных и распределение вейвлет-коэффициентов для каждого масштаба в части их перекрытия с соответствующими распределениями обучающих образцов, чтобы получить геологическую интерпретацию подземной формации.
2. Способ по п.1, в котором обучающие образцы являются представляющими фации, идентифицируемые геологом.
3. Способ по п.1, в котором один или несколько масштабов являются сравнимыми с масштабами длины изменений характеристик измеренных данных.
4. Способ по п.1, дополнительно содержащий повторение выполнения сегментации, вычисление распределения данных и вейвлет-коэффициентов и анализ распределения итерационным методом до удовлетворения заданному условию.
5. Способ по п.1, в котором вейвлет-преобразование применяют к каждой трассе измерений от многотрассового измерительного прибора и распределение вейвлет-коэффициентов вычисляют, собирая вейвлет-коэффициенты из всех трасс.
6. Способ по п.1, в котором измеренные данные или производные данные повторно корректируют после применения вейвлет-преобразования.
7. Способ по п.1, в котором сегментацию данных выполняют, разделяя скважинные каротажные данные на интервалы, по существу, равной длины, которые могут перекрываться на заданной фиксированной длине.
8. Способ по п.1, в котором анализ включает в себя для каждого сегмента и каждого масштаба определение фации, указанной распределением вейвлет-коэффициентов для сегмента и масштаба, в качестве фации, представленной обучающими образцами, чье соответствующее распределение вейвлет-коэффициентов наиболее близко соответствует вычисленному распределению вейвлет-коэффициентов в сегменте.
9. Способ по п.8, в котором соответствие между вычисленным распределением вейвлет-коэффициентов и распределением вейвлет-коэффициентов одного из обучающих образцов основано на мере подобия с использованием статистики хи-квадрат.
10. Способ по п.8, в котором анализ дополнительно включает в себя, для каждого сегмента, определение фаций, указанных распределением измеренных или вычисленных данных в качестве фаций, представленных обучающими образцами, чьи соответствующие распределения данных наиболее близко соответствуют распределению измеренных или производных данных.
11. Способ по п.10, в котором соответствие распределения измеренных или производных данных и распределение данных обучающих образцов основаны на мере подобия с использованием статистики хи-квадрат.
12. Способ по п.1, в котором вейвлет-преобразование применяют к каждой трассе многотрассовых данных, а анализ включает в себя группирование многотрассовых данных в группы трасс, которые измеряют в пространственной близости друг к другу вокруг буровой скважины, и для каждого масштаба, каждого сегмента и каждой группы трасс определение фации, указанной распределением вейвлет-коэффициентов для масштаба, сегмента и группы трасс, в качестве фации, представленной обучающими образцами, чье соответствующее распределение вейвлет-коэффициентов при этом масштабе наиболее близко соответствует распределению вейвлет-коэффициентов измеренных или производных данных для данного масштаба, данного сегмента и данной группы трасс, при этом указанные фации из каждой группы распределений трасс из данных и вейвлет-коэффициентов для каждого масштаба для данного сегмента сравнивают, чтобы предположить, что их изменчивость вокруг буровой скважины означает фацию разрывного типа, и если их изменчивость означает фацию разрывного типа, фацию, указанную распределением вейвлет-коэффициентов из всех трасс в сегменте, определяют как разрывную фацию.
13. Способ по п.1, в котором анализ включает в себя выполнение конечной идентификации фации для каждого сегмента путем использования правил, которые точно определяют конечную фацию для сегмента на основании фации, указанной распределением вейвлет-коэффициентов, на основании фации, указанной распределениями измеренных или производных данных или обоих, в котором распределения вейвлет-коэффициентов и распределения измеренных или производных данных вычисляют для сегмента в целом или для групп трасс в этом сегменте.
14. Способ по п.13, в котором правила включают в себя различение множества классов, каждый из которых включает в себя по меньшей мере одну фацию, при этом каждая фация приписана к одному или нескольким классам на основании фаций, указанных распределениями вейвлет-коэффициентов для сегментов при различных масштабах и распределением измеренных или производных данных или обоих.
15. Способ по п.14, в котором правила включают в себя первое определение одного первичного свойства в качестве измеренного или вычисленного свойства, чье распределение само идентифицирует каждую фацию из большого набора или поднабора фаций обучающих образцов.
16. Способ по п.15, в котором правила включают в себя конечную идентификацию фаций для заданного сегмента в качестве фаций, указанных распределением сегмента первичного свойства, если указанная фация принадлежит большому набору или поднабору фаций, идентифицируемых одним первым распределением свойства.
17. Способ по п.16, в котором правила включают в себя идентификацию масштаба wj из масштабов, используемых при вычислении вейвлет-преобразования, который является наиболее близким к масштабу cj характеристической длины (где j=1, 2, …, n) пространственной изменчивости данных из обучающих образцов, где n является количеством фаций, которые не идентифицируются одним распределением первичного свойства.
18. Способ по п.17, в котором правила включают в себя определении фации k2 для данного сегмента на основании (а) фации k1, указанной первичным распределением признака этого сегмента, и (b) фаций k2j (для каждого j=1, …, n), указанных соответствующим распределением вейвлет-коэффициентов в масштабе wj, если (i) фация k2 может идентифицироваться упорядоченной парой указанных фаций (k1, k2j), и (ii) фация k1 не принадлежит к большому набору или поднабору фаций, идентифицируемых этим одним распределением первичного свойства.
19. Способ по п.18, в котором правила включают в себя определение конечной фации этого сегмента посредством определения, какая фация наиболее связана с имеющей ту же упорядоченную тройку идентифицированной фацией, как и указанная упорядоченная тройка сегмента фаций (k1, k2j, k3k), указанных (а) распределением первичного свойства, (b) распределением соответствующих вейвлет-коэффициентов в масштабе длины wj, (с) распределением вейвлет-коэффициентов в другом масштабе длины wk соответственно, если фация не является идентифицируемой посредством (i) распределения одного первичного свойства или посредством (ii) упорядоченной пары указанных фаций (k1, k2j) при любом из масштабов wj.
20. Способ по п.1, в котором вейвлет-преобразование представляет собой ортогональное вейвлет-преобразование.
21. Способ по п.20, в котором вейвлет-преобразование представляет собой вейвлет Добеши второго порядка.
22. Способ по п.1, в котором измеряемая физическая величина представляет собой электрический сигнал, а характеристика является удельным сопротивлением или импедансом подземной формации.
23. Способ по п.1, в котором измеряемая физическая величина представляет собой сигнал гамма-излучения, а характеристика является естественным гамма-излучением подземной формации.
24. Компьютерный носитель информации, имеющий выполняемые машиной команды, при этом команды выполняются машиной для осуществления способа анализа характеристик подземной формации, этот способ содержит
применение вейвлет-преобразования к измеренным данным или к производным данным, полученным на основании измеренных данных, или к части их, при этом измеренные данные получены измерением по меньшей мере одного физического параметра на каждом из множества мест в буровой скважине, которая проходит через область подземной формации;
выбор одного или нескольких масштабов для анализа вейвлет-коэффициентов при каждом масштабе;
выполнение сегментации измеренных или производных данных;
вычисление распределения вейвлет-коэффициентов для каждого масштаба для одного или нескольких пространственных направлений применения вейвлет-преобразования, для вейвлет-преобразования измеренных или производных данных и для каждого сегмента, который принадлежит к участку, относительно которого было вычислено вейвлет-преобразование; и
для каждого сегмента анализируют распределение измеренных или производных данных и распределение вейвлет-коэффициентов для каждого масштаба в части их перекрытия с соответствующими распределениями обучающих образцов, чтобы получить геологическую интерпретацию подземной формации.
Текст
СПОСОБ И КОМПЬЮТЕРНЫЙ НОСИТЕЛЬ ИНФОРМАЦИИ ДЛЯ АНАЛИЗА ХАРАКТЕРИСТИК ПОДЗЕМНОЙ ФОРМАЦИИ В изобретении способ анализа характеристик подземной формации включает в себя применение вейвлет-преобразования к измеренным данным или к производным данным, полученным на основании измеренных данных, при этом измеренные данные получены измерением физического свойства на каждом из множества мест в буровой скважине, которая проходит через подземную формацию; выбор одного или нескольких масштабов для анализа вейвлет-коэффициентов; выполнение сегментации данных; вычисление распределения вейвлет-коэффициентов для каждого масштаба, для одного или нескольких пространственных направлений применения вейвлет-преобразования, для вейвлет-преобразования данных и для каждого сегмента, который принадлежит к участку, относительно которого вейвлет-преобразование было вычислено; и для каждого сегмента анализ распределения данных и распределения вейвлет-коэффициентов для каждого масштаба в части их перекрытия с соответствующими распределениями обучающих образцов для получения геологической интерпретации подземной формации. Область техники, к которой относится изобретение Настоящее изобретение относится к определению характеристик геологических данных, а более конкретно к автоматизированной интерпретации скважинных каротажных данных. Предшествующий уровень техники Скважинные данные собирают с помощью некоторого количества способов, включающих, например, измерения удельного сопротивления/удельной проводимости, ультразвуковые измерения, измерения ядерного магнитного резонанса и рассеяния излучения. Обычно скважинные данные анализирует человек-интерпретатор, чтобы определять характеристики подземной геологической формации, что позволяет принимать решения относительно потенциала скважины или находить информацию о характере окружающей геологической области. Скважинные данные этого вида можно использовать вместо сбора кернового материала, предназначенного для непосредственного изучения, или в дополнение к нему. Краткая сущность изобретения Согласно одному аспекту изобретения предложен способ анализа характеристик подземной формации, включающий применение вейвлет-преобразования к измеренным данным или к производным данным, полученным на основании измеренных данных, или к части их, при этом измеренные данные получены измерением по меньшей мере одного физического свойства на каждом из множества мест в буровой скважине, которая проходит через область подземной формации; выбор одного или нескольких масштабов для анализа вейвлет-коэффициентов при каждом масштабе; выполнение сегментации измеренных или производных данных; вычисление распределения вейвлет-коэффициентов для каждого масштаба, для одного или нескольких пространственных направлений применения вейвлет-преобразования, для вейвлет-преобразования измеренных или производных данных и для каждого сегмента, который принадлежит к участку, относительно которого было вычислено вейвлет-преобразование; и для каждого сегмента анализ распределения измеренных или производных данных и распределения вейвлеткоэффициентов для каждого масштаба в части их перекрытия с соответствующими распределениями обучающих образцов, чтобы получить геологическую интерпретацию подземной формации. Согласно другому аспекту изобретения предложен компьютерный носитель информации, имеющий выполняемые машиной команды, при этом команды выполняются машиной для осуществления способа анализа характеристик подземной формации, при этом способ включает вычисление распределения вейвлет-коэффициентов для каждого масштаба, для одного или нескольких пространственных направлений применения вейвлет-преобразования, для вейвлет-преобразования измеренных или производных сегментированных данных и для каждого сегмента, при этом измеренные данные получены измерением по меньшей мере одного физического свойства на каждом из множества мест в буровой скважине, которая проходит через область подземной формации, и производные данные получены на основании измеренных данных; и для каждого сегмента анализ распределения измеренных или производных данных и распределения вейвлет-коэффициентов для каждого масштаба в части их перекрытия с соответствующими распределениями обучающих образцов. Краткое описание чертежей Эти и другие аспекты, признаки и характеристики настоящего изобретения, а также способы выполнения действий, функции связанных элементов структуры, сочетания частей и экономические показатели процесса изготовления станут более понятными при рассмотрении нижеследующего описания и прилагаемой формулы изобретения с обращением к сопровождающим чертежам, которые все образуют часть этого описания, при этом одинаковыми позициями обозначены аналогичные элементы на различных чертежах. Однако следует определенно понимать, что чертежи предназначены только для иллюстрации и описания и не предполагаются определяющими пределы изобретения. Используемая в описании и формуле изобретения сингулярная форма неопределенных и определенных артиклей включает в себя множество объектов, если только из контекста ясно не следует иное. На чертежах: фиг. 1 - иллюстрация в общих чертах способа анализа характеристик подземной формации согласно осуществлению изобретения; фиг. 2 - вид примера обычного скважинного зонда; фиг. 3 а и 3b - виды сбоку и спереди соответственно участка датчиков зонда, показанного на фиг. 2; фиг. 4 - схематический вид зонда, находящегося в связи с компьютером, согласно осуществлению изобретения; фиг. 5 а - изображения диаграммы гамма-каротажа (столбец 1), интерпретированных вручную геологических фаций (столбец 2), нормированных трасс удельного сопротивления (столбец 4), границ, полученных в результате сегментации обычным алгоритмом segwave (алгоритмом сегментации каротажных данных изображений удельного сопротивления), использованным для проверки способа классификации (столбец 5), распределения удельного сопротивления (столбец 6), распределения вейвлеткоэффициентов для масштаба 1/16 фута (1,905 см) (столбцы 7-9) и для масштаба 1/8 фута (3,81 см)(столбцы 10-12) и результатов промежуточной классификации (столбцы 13-23) в зависимости от глубины в буровой скважине (столбец 3) согласно осуществлению изобретения; фиг. 5b - изображения диаграммы гамма-каротажа (столбец 1), интерпретированных вручную гео-1 019763 логических фаций (столбец 2), нормированных трасс удельного сопротивления (столбец 4), границ, полученных в результате сегментации обычным алгоритмом segwave (алгоритмом сегментации каротажных данных изображений удельного сопротивления), использованным для проверки способа классификации (столбец 5), распределения удельного сопротивления (столбец 6), распределения вейвлеткоэффициентов для масштаба 1/16 фута (1,905 см) (столбец 7) и для масштаба 1/8 фута (3,81 см) (столбец 8) и результатов промежуточной классификации (столбцы 9-19) в зависимости от глубины в буровой скважине (столбец 3) согласно осуществлению изобретения; фиг. 6 - иллюстрация способа выполнения извлечения признаков и промежуточной классификации для каждого сегмента согласно осуществлению настоящего изобретения; фиг. 7 а и 7b - иллюстрация классов для слияния признаков и конечной классификации в глубинной обстановке с семью фациями согласно осуществлению изобретения; фиг. 8 - иллюстрация способа выполнения слияния признаков и конечной классификации согласно осуществлению изобретения; фиг. 9 - иллюстрация способа слияния признаков и конечной классификации согласно осуществлению изобретения и фиг. 10 - иллюстрация способа образования правила согласно осуществлению изобретения. Подробное описание вариантов воплощения изобретения Скважинные данные анализируют, чтобы определить геологический профиль подземной формации. Скважинные данные получают, измеряя и регистрируя в буровой скважине физические величины при скважинном каротаже. Этими физическими величинами обеспечивается информация о различных текстурах материалов (фаций), которые образуют геологический профиль подземной формации. Для анализа скважинных данных обычно необходима значительная активность человека и может требоваться очень много времени. Поэтому желательно, чтобы этот анализ был, по меньшей мере, полуавтоматическим. Анализ скважинных изображений выполняют посредством основанной на диаграмме кластеризации с переменной разрешающей способностью (см. патент США 6295504, Ye and Rabiller). Помимо трудностей адекватного согласования автоматической интерпретации с интерпретацией человеком, которые вносит кластеризация, также существует большая проблема при текстурном анализе, заключающаяся в определении ограниченного количества параметров при моделировании текстур, которые позволяют адекватно различать и синтезировать визуально подобные образцы. Современные теории различения текстур включают в себя идею, заключающуюся в том, что две текстуры часто трудно различить(например, подобные), когда они создают аналогичное распределение откликов в банке (ориентационных и пространственно-частотных селективных) линейных фильтров (Heeger and Bergen, "Pyramid basedspectral histograms", Image Processing, IEEE Transactions, vol. 12, issue 6, June 2003). В аспекте изобретения, представленном ниже, при классификации фаций на основании скважинных каротажных данных используют вейвлет-преобразование скважинных каротажных сигналов, и она основана на подобии распределений коэффициентов вейвлет-преобразования сегментированных данных соответствующим распределениям обучающих образцов фаций, при этом обучающие образцы могут предоставляться экспертом и оставаться неизменными в продолжение применения. В этом способе классификацию выполняют строго в рамках распознанных экспертом фаций и трудности согласования результатов автоматической интерпретации с результатами человека-интерпретатора значительно уменьшаются. Вейвлет-преобразование представляет собой линейное преобразование, при котором выполняют свертку исходного сигнала с семейством функций или вейвлетов нулевого среднего, которые удовлетворяют известному условию допустимости (см. Stephane Mallat "A wavelet tour of signal processing", p. 82,Academic Press, 2nd Edition, 1999). Функции, принадлежащие к семейству вейвлетов, являются взаимно подобными по форме, но перемещаемыми и/или растягиваемыми во времени (или по глубине) переменными. Результат вейвлет-преобразования выражают вейвлет-коэффициентами, которые индексируют положением (в котором вейвлет центрируют) и масштабом (который характеризует ширину вейвлета). Как показано в уравнении (1), семейство вейвлетов получают на основании материнского вейвлета (t),сдвигая его на х и масштабируя его на а: После того как семейство вейвлетов выбрано, непрерывное вейвлет-преобразование функции f(t) задают в виде (см. уравнение (2: где Wf(x,a) - вейвлет-коэффициенты. В большей части применений семейств вейвлетов используют их способность эффективно аппроксимировать конкретные классы функций небольшим количеством ненулевых вейвлет-коэффициентов(см. "A wavelet tour of signal processing" на с. 241), коэффициентами небольшой величины при мельчайших масштабах, обычно соответствующих гладким частям сигнала. Наряду с другими применениями вейвлет-преобразование является полезным при определении характеристик скачкообразных изменений сигнала (через коэффициенты большой, локально максимальной величины вокруг местоположений таких изменений). В осуществлении изобретения вейвлет-преобразование, применяемое к исходному сигналу, является дискретным. Однако должно быть понятно, что непрерывное вейвлет-преобразование также можно применять к измеряемым сигналам. Дискретное вейвлет-преобразование отличается от непрерывного вейвлет-преобразования тем, что свертку выполняют не в виде интеграла, а в виде суммы по дискретным точкам х, отстоящим друг от друга в соответствии с заданным масштабом а. В осуществлении изобретения, описанном в этом патенте, сегменты данных классифицируют в соответствии с заданным подобием, строго следуя обучающим образцам фаций, предоставляемым экспертом. Таким способом трудности согласования результатов автоматической интерпретации с результатами человека-интерпретатора значительно уменьшаются. Фации, которые изучают, могут быть литофациальными сегментами размером до 1 фута (30,48 см) (если только они имеют относительно хорошо определенные, поддающиеся измерению свойства породы, которые по мнению экспертов позволяют считать их независимыми друг от друга) или более крупными депофациальными сегментами из литофациальных агрегатов. На фиг. 1 показан в целом способ анализа характеристик подземной формации согласно осуществлению изобретения. Способ начинают с действия 10, при выполнении которого измеряют одну или несколько физических величин на каждом из множества мест в буровой скважине, которая проходит через область подземной формации. Физические величины можно измерять, используя зонд, такой как показан на фиг. 2. Зонд может быть многотрассовым или многоконтактным измерительным зондом. Например, на фиг. 2 показан зонд 100, предназначенный для использования при определении характеристик буровой скважины, который включает в себя обычно удлиненный стержень 120, имеющий на одном конце некоторое количество выдвигающихся наружу элементов 140. Каждый из выдвигающихся наружу элементов 140 может включать в себя датчик 160 (показанный более подробно на фиг. 3 а и 3b) для исследования области 180 буровой скважины. Показанный датчик 160 включает в себя множество пар датчиков 200 для контроля изменения напряжения, которое возникает на участке 220 области 180, когда ток инжектируют через электроды 240 инжектора тока. Хотя датчик 160, показанный на фиг. 3 а и 3b, выполнен и приспособлен для измерения электрических характеристик скважинного материала, это сделано только с целью иллюстрации, и в различных осуществлениях настоящего изобретения можно использовать широкий ассортимент датчиков. В частности, предполагается, что можно использовать измерения удельного сопротивления, ультразвуковых или других акустических волн, комплексного электрического импеданса, коэффициента отражения или пропускания нейтронов, ядерного магнитного резонанса, изображений и/или спектрометрии. Кроме того,можно измерять эмиссию естественного гамма-излучения. В соответствии с этим датчик 160 может выбираться согласно выполняемому измерению и может включать в себя в качестве не создающего ограничений примера электрические источники и детекторы, источники излучения и детекторы и акустические преобразователи. Должно быть понятно, что может быть полезно включать в единственный зонд 100 датчики многочисленных видов и таким путем может быть полезно использовать различные сочетания. При использовании зонд 100 обычно спускают в буровую скважину, характеристики которой должны быть определены. После достижения надлежащей глубины, которая может соответствовать забою скважины, или выбранной промежуточной глубине, зонд поднимают из скважины и измерения выполняют по мере того, как зонд поднимают через материал. Во многих случаях зонд 100 имеет четыре датчика 160, так что скважину можно характеризовать в каждом из четырех направлений, которые, например, можно обозначить как 0, 90, 180 и 270. Работа зонда 100 будет описана на примере использования электрических датчиков, показанных на фиг. 3 а и 3b. Хотя в этом изобретении подробно описываются измерения удельного сопротивления, детали будут меняться в соответствии с конкретным датчиком, используемым в данной реализации. На датчике 100 получают измерения при передаче от электродов 240 электрического сигнала, который может быть постоянным током, или переменным током, или иным образом изменяющимся током I, по меньшей мере, частично в область 180 материала буровой скважины. Как должно быть понятно, глубина проникновения сигнала отчасти зависит от вида измерения. Для измерения коэффициента отражения практически не требуется глубина проникновения в материал при исследовании, тогда как для измерения удельного сопротивления необходимо, чтобы сигнал распространялся на некоторое расстояние через материал. Однако должно быть понятно, что каждая из упомянутых выше степеней проникновения находится в объеме настоящего изобретения. В особом случае измерения удельного сопротивления в буровом растворе на нефтяной основе сигнал распространяется через материал и принимается датчиками 200. Датчиками 200 измеряют изменениеV напряжения на участке 220 области 180, которое показывает характеристику (удельное сопротивление в этом случае) материала, который присутствует в характеризуемой подземной формации. В варианте осуществления удельное сопротивление R материала на участке 220 можно вычислить по формуле: где I является током, создаваемым электродами 220, и k представляет собой геометрический коэф-3 019763 фициент, который можно задать на основании геометрии электродов 240 и датчиков 220. Как должно быть понятно, эта формула зависит от относительной однородности материала в промежутке между электродами 240. По этой причине масштабный коэффициент k может быть реализован в виде динамического масштабного коэффициента, что может дать дополнительные подробности. Как показано на фиг. 4, скважинные данные, собираемые зондом, обычно сохраняют в локальном запоминающем устройстве, например в снабженных памятью приборах каротажа в процессе бурения,или передают по проводам, хотя соединение может быть беспроводным, в компьютер 250, который можно расположить, например, на буровой установке, при этом данные могут приниматься по шине 260 компьютера 250, который может быть любого подходящего типа, и сохраняться, например, в считываемом компьютером устройстве 270 хранения данных, таком как жесткий диск, оптический диск, флэшпамять, оперативная память для временного хранения или другие среды, для обработки процессором 280 компьютера 250. Как показано на фиг. 5 а-5b в столбце 4 под заголовком "Все трассы", скважинные данные могут быть преобразованы в графическую форму, в форму данных 520 изображений для отображения и/или дополнительной обработки. Графические данные можно сохранять как полноцветные данные (например,24-разрядные данные в стандарте JPEG) или как одноцветные или полутоновые данные. Данные 520 изображений из фиг. 5 а и 5b представляют трассы удельного сопротивления, полученные на каждом из множества мест в буровой скважине прибором OBMI (формирователем микроизображений при наличии бурового раствора на нефтяной основе) от Schlumberger. В столбце 3 под заголовком "Глубина в футах" на фиг. 5 а и 5b показан соответствующий участок 515 глубин (от 450 до 520 футов, от 137,6 до 158,496 м) буровой скважины, для которого получены данные 520 изображений. Эти трассы удельного сопротивления являются нормированными. Цвет придан значению удельного сопротивления, измеренного датчиком, чтобы получить картину удельного сопротивления. Данные 520 изображений включают в себя четыре полосы 521a-d, продолжающиеся вниз по столбцу 4 на фиг. 5 а и 5b. Эти четыре полосы представляют данные от четырех прижимных измерительных башмаков с датчиками, полученные с помощью зонда 100, при этом каждый прижимной измерительный башмак с датчиком обеспечивает пять трасс данных. Более темные участки данных 520 изображений представляют относительно проводящие области, а более светлые участки представляют относительно резистивные области. В обломочных породах более темные, более проводящие области можно интерпретировать как слоистые аргиллиты, тогда как более светлые, более резистивные области могут быть песчаными областями. В карбонатных породах и при смешанной литологии текстура изображений удельного сопротивления и физические величины, а не среднее удельное сопротивление, становятся более важными для различения литофаций, а также депофаций. Распределения физических свойств, измеряемых зондом 100, можно получать как функцию глубины. Например, на основании результатов измерений удельного сопротивления (например, данных 520 изображений в столбце 4 из фиг. 5 а и 5b) можно получать распределение или гистограмму удельного сопротивления как функцию глубины в буровой скважине. Распределение 530 удельного сопротивления,вычисленное на интервалах глубин 1 фут (30,48 см), показано в столбце 6 из фиг. 5 а и 5b. На этой гистограмме или распределении 530 удельного сопротивления отражена яркость изображений для четырех трасс 521a-d. Аналогичные распределения можно получить для других измеренных или вычисленных величин на интервалах глубин соответствующей протяженности. Снова обратимся к фиг. 1, где после измерения одного или нескольких физических свойств на каждом из множества мест в буровой скважине, которая проходит через область подземной формации (и при желании вычисления других производных величин на основании измеряемых данных), в способе переходят к действию 20, при выполнении которого вейвлет-преобразование применяют к измеренным или производным данным или к части их. В случае изображений удельного сопротивления вейвлетпреобразование можно применять в направлении вдоль оси буровой скважины, то есть независимо относительно каждой трассы каждой площадки 521a-d или относительно последовательности данных, образованных на основании интерполированных данных, которые лежат на кривой (или участке ее, соответствующем изображению на прижимном измерительном башмаке прибора, если прибор имеет прижимные измерительные башмаки), построенной на основании наблюдаемого из скважины изображения (то есть при наличии каждой трассы, расположенной в порядке появления в пространстве вокруг буровой скважины) в виде поперечного сечения стенки буровой скважины и плоскости напластования или другой плоскости, представляющей интерес. В случае, когда сегмент буровой скважины является идеальным цилиндром, эта кривая обычно представляет собой синусоиду. Вычисление вейвлет-преобразования вдоль двух направлений является локально подобным двумерному вейвлет-преобразованию, но направление применения, которое не находится вдоль оси буровой скважины, можно постепенно изменять,чтобы оно оставалось параллельным напластованию. В осуществлении изобретения вейвлет-преобразование представляет собой дискретное вейвлетпреобразование, хотя предполагается, что в другом осуществлении изобретения также можно применять непрерывное преобразование. Вейвлет-преобразование может быть ортогональным. Например, вейвлет Добеши второго порядка можно использовать в качестве производящей вейвлет-функции. Должно быть понятно, что в других осуществлениях изобретения можно использовать другие вейвлет-функции. При выполнении действия 30 (фиг. 1) определяют последовательность масштабов для анализа вейвлет-коэффициентов, чтобы захватить резкие изменения сигнала при различных масштабах. Например, вейвлет-коэффициенты можно получать для трех различных масштабов: первого масштаба, второго масштаба, превышающего в два раза первый масштаб, и третьего масштаба, превышающего в два раза второй масштаб. Желательно, чтобы выбираемые при выполнении действия 30 масштабы были сравнимыми с масштабами длины характеристических интрафациальных изменений измеренных данных, поскольку вейвлет-коэффициенты при таких масштабах будут наиболее близко соответствовать изменениям исходного сигнала, происходящим при этом масштабе, и поэтому будут соответствовать сигнатуре фации в такой степени, в какой эта сигнатура присутствует в измеренных данных. В осуществлении величину масштабов можно выбирать визуально при рассмотрении мелкомасштабных изменений данных 520 изображений, которые можно интерпретировать геологически (то есть без учета связанных с шумом изменений). То есть небольшие масштабы выбирают для представления доступных собственных изменчивостей фаций, которые также обусловлены разрешением анализируемых скважинных каротажных данных. Например, что касается фиг. 5 а, то примерно десять тонких слоев можно видеть на данных первой площадки от 480 до 482 футов (от 146,304 до 146,9136 м). По этой причине в осуществлении для анализа каротажных данных 520 изображений удельного сопротивления можно использовать вейвлет-коэффициенты в масштабе 1/16 фута (1,905 см) и 1/8 фута (3,81 см). Для различных подземных условий можно выбирать дополнительные и/или другие масштабы (например, 1/2 фута (15,24 см), 1/4 фута (7,62 см) и 1/32 фута(0,9525 см. Кроме того, выбор масштабов можно автоматизировать с помощью программного обеспечения или программы, которая автоматически определяет наиболее релевантные величины масштаба. Такое программное обеспечение или программа может анализировать среднее и дисперсию энергии вейвлета при каждом масштабе на основании некоторого, ранее выбранного набора масштабов на протяжении фиксированных интервалов глубины вокруг различных мест в буровой скважине. В таком случае более репрезентативными масштабами для выбора являются масштабы, при которых дисперсия энергии вейвлета в расчете на сегмент в буровой скважине не меньше средней энергии в расчете на сегмент, где, как будет рассмотрено ниже, длина сегмента соответствует разрешению данных и минимальной протяженности литофациальных единиц, подлежащих распознаванию при классификации. После выбора различных масштабов для анализа распределения вейвлет-коэффициентов в способе(фиг. 1) переходят к действию 40, при этом выполняют сегментацию измеренных или производных скважинных данных. Скважинные данные (например, данные 520 изображений) сегментируют на основании, например, однородности локальных участков. Скважинные каротажные данные, такие как данные 520 об удельном сопротивлении, сегментируют в соответствии с любым из доступных способов сегментации, признанным достаточно чувствительным для имеющихся данных, или просто путем равномерного разбиения. Сегментация может включать в себя этап перегруппировки по глубине каротажных данных(включающих в себя трассы каротажной диаграммы от многоконтактного прибора), чтобы границы геологических слоев, полученные на основании различных каротажных данных, обнаруживались на одной и той же глубине. Этот этап можно выполнять при крупном масштабе во время предварительной обработки или одновременно с сегментацией, вследствие чего перегруппировку можно изменять локально. Последний процесс является подходящим для способов локальной сегментации, но также может использоваться при повторениях способа глобальной сегментации. Информацию относительно того, где границы сегментов находятся в буровой скважине, сохраняют в виде 0 (без изменения) или 1 (граница сегмента) в одномерном массиве при наличии в достаточной степени чувствительной выборки из буровой скважины(например, через 1/4 фута (7,62 см) для глубоководных турбидитов). В осуществлении масштабный параметр сегментации можно выбирать так, чтобы сегменты были размера, подходящего для выполняемого анализа, то есть пропорционального разрешению измерений и предпочтительно не больше минимального размера литофациальных единиц, которые необходимо распознавать. Это означает, что размер сегмента должен быть достаточно большим, чтобы имелось большое количество точек данных для формирования гладкого распределения, но не слишком большим, чтобы были включены многочисленные литофациальные единицы. Например, размер сегмента от 1 до 3 футов (от 30,48 до 91,44 см) является подходящим для анализа гистограммы изображения удельного сопротивления, получаемого приборомOBMI (формирователем микроизображений при наличии бурового раствора на нефтяной основе), при наличии 40 бинов и распознавании литофациальных единиц на основании такой гистограммы. В случае измерений единственной трассы с грубым разрешением, например обнаружения естественного гаммаизлучения (столбец 1 из фиг. 5 а и 5b), размер сегмента должен быть по меньшей мере в 10 раз больше,чем разрешение измерений, при этом исключается обнаружение и распознавание тонкослойных фаций на основании только гамма-излучения. В одном осуществлении блоки больше 3 футов (91,44 см) можно дополнительно разрывать на 3 сегмента длиной 1 фут (30,48 см) с остатком не больше 3 футов (91,44 см). В дальнейшем осуществлении длина каждого сегмента по меньшей мере примерно в 30 раз больше, чем ожидаемое регулярное разнесение точек измерений в буровой скважине. В дальнейшем осуществлении сегментацию выполняют, точно определяя положения центров интервалов равной длины, которые перекрываются на заданном фиксированном отрезке (связанном с различием между разрешением измерений, умноженным на 10, и минимальной протяженностью литофациальной единицы). Это осуществление может быть предпочтительным в случае измерений с грубым разрешением, поскольку положения центров интервалов могут находиться значительно ближе, чем длина интервала, необходимая для получения гладкого распределения измеренных данных. Эти интервалы используют в способе на этапе классификации так, как если бы они были неперекрывающимися сегментами. Для тех областей буровой скважины, где обнаруживают перекрывающиеся интервалы, принадлежащие к различным фациям, процедуры сегментации и классификации повторяют, чтобы уточнить местоположения границ. Для данной пары интервалов каждая новая тройка состоит из: 1) классификации этих интервалов при их текущих положениях центров, затем 2) классификации после совместного сдвига местоположений центров перекрывающихся интервалов, в результате чего выполняется небольшой сдвиг сначала к одному концу буровой скважины, и далее 3) классификации после сдвига к другому концу буровой скважины при небольшой фиксированной длине d этапа итерации. Если сдвиг в одном направлении вызывает изменение классификации одного интервала, в то время как другая классификация является стабильной, и сдвиг в противоположном направлении не приводит к результатам, отличающимся от результатов для центрального положения интервалов, то следующая тройка итераций будет начинаться от центрального положения интервалов, сдвинутых относительно центрального положения в результате предшествующей тройки итераций на длину d этапа итерации (или его часть, если желательна высокая степень точности) в направлении этого интервала, что изменяет его фациальную принадлежность. Если оба сдвига (то есть в обоих направлениях) приводят к одинаковому количеству интервалов, изменяющих принадлежность, и если это количество равно двум или нулю (оба интервала изменяют фациальную принадлежность или не изменяют), итерационный процесс прекращают и местоположение границы для этой пары сегментов выбирают как центральную точку между местоположениями центров интервалов в их центральном положении при последней тройке итераций. В случаях, отличающихся от описанных в этом изобретении результатов для троек итераций, делают вывод, что интервалы являются слишком большими, вследствие чего несколько границ оказывают влияние на классификацию (то есть выбраны несколько границ вместо только одной, при этом результаты классификации соответствуют интервалам,центрированным посередине между этими границами), или длина этапа итерации является слишком большой, и итерационный процесс можно начать повторно при меньшей длине этапа. После нахождения стабильных границ в соответствии с этой процедурой перекрывающиеся сегменты, для которых имеются одинаковые результаты классификации, объединяют. После сегментации скважинных каротажных данных при выполнении действия 50 определяют распределение вейвлет-коэффициентов для каждого масштаба вейвлета, выбранного при выполнении действия 30, для одного или нескольких направлений применения вейвлет-преобразования и для каждого сегмента, который принадлежит к участку, для которого вычисляли вейвлет-преобразование. На фиг. 5 а в столбцах 7, 8 и 9 показаны распределения вейвлет-коэффициентов для масштаба 1/16 фута (1,905 см) и для различных размеров сегментов: 3 фута (91,4 4 см) для данных в логарифмическом масштабе (столбец 7) и 1 фут (30,48 см) (столбцы 8 и 9). В столбце 8 распределения вейвлет-коэффициентов нанесены в логарифмическом масштабе, тогда как в столбце 9 они нанесены в линейном масштабе. Столбцы 10, 11 и 12 аналогичны столбцам 7, 8 и 9 соответственно, за исключением того, что они привязаны к масштабу 1/8 фута (3,81 см). Самые разные литофации в части изменчивости измеряемых величин, использованные для классификации (например, с весьма различной текстурой изображения удельного сопротивления) имеют распределения вейвлет-коэффициентов, которые являются в значительной степени различными по форме. Например, как видно на фиг. 5 а, распределение вейвлет-коэффициентов в масштабе 1/16 фута(1,905 см) в столбце 7 имеет существенно различающиеся формы около 454,5 фута (138,5316 м) и 493,5 фута (150,4188 м). Точно так же распределение вейвлет-коэффициентов в масштабе 1/8 фута (3,81 см) в столбце 10 имеет существенно различающие формы около 454,5 фута (138,5316 м) и 493,5 фута(150,4188 м). Затем после вычисления распределения вейвлет-коэффициентов для каждого масштаба вейвлета и сегмента в способе переходят к действию 55, при выполнении которого распределения вейвлеткоэффициентов для каждого масштаба вычисляют для обучающих образцов различных выбранных известных фаций. После этого в способе переходят к действию 60, при выполнении которого распределения вейвлет-коэффициентов и распределение (распределения) скважинных данных (например, распределение 530 удельного сопротивления в столбце 6 фиг. 5 а) для каждого сегмента анализируют в части их перекрытия с соответствующими распределениями обучающих образцов (вычисленными при выполнении действия 55), чтобы получить геологическую интерпретацию подземной формации. При этом анализе получают геологическую интерпретацию подземной формации в отношении единиц, которые различаются по сигнатуре каротажной диаграммы и геологическому строению. В осуществлении изобретения действие 60 включает в себя два основных аспекта. Первый аспект состоит из этапа извлечения признака (на основании согласования всех распределений сегментов измеренных данных и их вейвлет-коэффициентов с соответствующими распределениями данных обучающих образцов) и промежуточной классификации для каждого сегмента буровой скважины. Второй аспект состоит из этапа слияния признаков и конечной классификации. В осуществлении обучающие образцы, которые рассматриваются при выполнении действия 55, находятся в том же самом массиве измеренных данных и предоставляются человеком-интерпретатором с обозначением их начальной и конечной глубин. Кроме того, обучающие образцы можно получать из ранее запомненной библиотеки. В этом последнем случае распределение вейвлет-коэффициентов для обучающих образцов можно иметь заранее. По меньшей мере один обучающий образец необходим для каждой фации. В другом осуществлении изобретения обучающие образцы находят (1) идентифицируя местоположения в измеренных данных, где находится локальный максимум или минимум вейвлеткоэффициентов в масштабе 1 или 2 фута (30,48 или 60,96 см) (или в сравнимом масштабе), абсолютное значение которого находится среди нескольких наибольших значений, вычисленных по этим данным; (2) вычисляя распределение измеренных данных или маломасштабных (например, в масштабе 1/8 фута (3,81 см) или сравнимом масштабе) вейвлет-коэффициентов для двух сегментов в масштабе 2 фута (60,96 см)(или сравнимом масштабе) возле каждого из таких местоположений (одного выше и одного ниже); (3) вычисляя перекрытия распределений для этой пары сегментов и (4) выбирая пару или меньшее количество этих сегментов с наименьшими взаимными перекрытиями распределений в качестве обучающих образцов. Чтобы выполнить этап извлечения признака из классификации, сначала вычисляют (действие 55) распределения (например, гистограммы) измеренных данных и вейвлет-коэффициенты, относящиеся к обучающим образцам. Распределения (например, гистограммы) вейвлет-коэффициентов, которые находятся в окнах очерченных обучающих образцов, вычисляют для каждого из небольшого количества отобранных масштабов вейвлетов (например, масштаба 1/16 или 1/8 фута (1,905 или 3,81 см, выбранных при выполнении действия 30, и для каждой из множества выбранных известных фаций (а также для каждого направления при использовании более утонченного способа). В осуществлении рассматривают семь обучающих образцов, представляющих известные геологические фации. В случае данных изображений коэффициенты вейвлет-преобразования для отдельных трасс данных также включают в то же самое распределение или гистограмму при условии, что их положения находятся в том же самом окне или соответствующим образом скорректированы по глубине. Одного обучающего образца длиной около 3 футов(91,44 см) из данных изображения удельного сопротивления может быть достаточно для каждой фации. Должно быть понятно, что если предоставляется большее количество обучающих образцов в расчете на фацию, одно распределение образуют в расчете на один масштаб, в расчете на фацию, добавляя реализации коэффициентов в некотором интервале величин во всех обучающих образцах для этой фации. В осуществлении из результатов этих вычислений, полученных с помощью обучающих образцов,представляющих известные геологические фации, создают три отдельные библиотеки или коллекции распределений: (1) первую библиотеку, включающую распределения вейвлет-коэффициентов для каждого из обучающих образцов (например, семи обучающих образцов) в масштабе 1/16 фута (1,905 см), (2) вторую библиотеку, включающую распределения вейвлет-коэффициентов для каждого из обучающих образцов (например, семи обучающих образцов) в масштабе 1/8 фута (3,81 см), и (3) третью библиотеку,включающую распределения скважинных данных (например, гистограммы амплитуд сигнала или гистограммы пикселов в случае изображения) для каждого из обучающих образцов (например, семи обучающих образцов). Затем эти библиотеки можно использовать для выполнения промежуточной классификации каждого из сегментов буровой скважины. На фиг. 6 показан способ выполнения извлечения признака и промежуточной классификации для каждого сегмента буровой скважины согласно осуществлению изобретения. Способ начинают с действия 610, при выполнении которого распределение вейвлет-коэффициентов для рассматриваемого свойства,для каждого из ранее выбранных репрезентативных масштабов (например, масштаба 1/16 или 1/8 фута(1,905 или 3,81 см образуют для каждого сегмента в буровой скважине. Это действие соответствует действию 50 из фиг. 1. Затем в способе переходят к действию 620, при выполнении которого вычисляют меру подобия между распределением вейвлет-коэффициентов данного образца при заданном масштабе и распределениями вейвлет-коэффициентов обучающего образца каждой фации при том же самом масштабе. Этот процесс повторяют для каждого масштаба и каждого сегмента. В осуществлении распределения вейвлет-коэффициентов измеренных или производных данных сравнивают с первой и второй библиотеками (например, при масштабе 1/16 или 1/8 фута (1,901 или 3,81 см, чтобы идентифицировать фации в первой и второй библиотеках, которые имеют распределение вейвлет-коэффициентов, наиболее близко соответствующее распределению вейвлет-коэффициентов, полученному с помощью сегментированных данных (см. действие 625). Статистику хи-квадрат можно использовать в качестве меры подобия для идентификации согласования обучающих образцов или фаций. Статистика хи-квадрат двух бинированных распределений определяется как (4),и Ri и Si представляют собой соответствующие некоторые количества первых и вторых событий распределения в i-м бине (то есть точек данных значения, принадлежащего к i-му бину),где i принимает значения целых чисел от 1 до v для индексирования тех и только тех пар бинов, где по меньшей мере одно из двух распределений имеет ненулевое количество событий, a v именуется числом степеней свободы. Размер бина выбирают так, чтобы v было намного больше 1 или количество событий в каждом бине было большим. При этих условиях функция хи-квадрат распределения, которая представляет собой неполную гамма-функцию, выражающую, что сумма квадратов v случайных нормальных переменных единичной дисперсии и нулевого среднего будет больше, чем 2, является хорошим приближением распределения 2 в уравнении (4) для случая нулевой гипотезы (то есть гипотезы, в соответствии с которой (нормированный) Ri и Si извлекают из одной и той же совокупности), а ее использование является стандартным (см. W.H. Press et al. "Numerical recipes in C", p. 621, Cambridge University Press, 1999). Небольшое значение указывает на то, что нулевая гипотеза скорее является маловероятной (то есть данные о конкретном образце и данные об обучающем образце имеют различные в виде выбросов для сегментов, показанных распределения). В столбцах 15 и 16 фиг. 5 а показана в столбце 5 (семь выбросов различного цвета в расчете на сегмент, по одному для каждой фации), для масштабов 1/16 фута (1,905 см) и 1/8 фута (3,81 см) соответственно. Столбцы 19 и 20 из фиг. 5 а аналогичны столбцам 15 и 16 соответственно с одним только различием, заключающимся в том, что обучающий образец для фации 8, присутствующей в области около 500 футов (152,4 м), был другим. показана в столбцах 11, 12, 15, 16 и 19 на фиг. 5b. Известную геологическую фацию с распределением вейвлет-коэффициентов для рассматриваемого свойства при заданном масштабе, которое наиболее близко согласовано (что определяется наибольшей хи-квадрат вероятностью при заданном числе степеней v свободы) с распределением вейвлеткоэффициентов данного сегмента при том же самом масштабе, выбирают в качестве результата промежуточной классификации сегмента на основании распределения вейвлет-коэффициентов рассматриваемого свойства при этом масштабе (см. действие 625) и эту фацию относят к фации, указанной для этого сегмента распределением вейвлет-коэффициентов рассматриваемого свойства при этом масштабе, или в качестве результата сравнения этого сегмента с распределением вейвлет-коэффициентов рассматриваемого свойства при этом масштабе. В столбце 14 фиг. 5 а показаны результаты такой промежуточной классификации для масштабов 1/8 фута (3,81 см), 1/16 фута (1,905 см) и 1/32 фута (0,9525 см), при этом код фации (пронумерованный как 0-12) является таким же, как код в столбце 2 в результате ручной интерпретации за исключением изменения масштаба на несущественный множитель 10. Столбец 18 из фиг. 5 а аналогичен столбцу 14, при этом единственное отличие заключается в обучающем образце для фации 8. Столбцы 21-23 из фиг. 5 а аналогичны столбцам 17-19 за исключением того, что сегменты больше 3 футов (91,44 см) разделены на три блока размером 1 фут (30,48 см) (с остатком). Затем после идентификации наиболее близких согласований для распределений вейвлеткоэффициентов при различных шкалах (например, с использованием первой и второй библиотек распределений) в способе переходят к действию 630, при выполнении которого вычисляют меру подобия между распределениями данных измеренного свойства буровой скважины или производной величины для данного образца (например, гистограмму амплитуд гамма-излучения или гистограмму пикселов изображения удельного сопротивления) и обучающих образцов для каждого сегмента в буровой скважине. Например, в осуществлении распределение 530 удельного сопротивления для каждого сегмента, показанное в столбце 6 из фиг. 5 а, сравнивают с распределениями удельных сопротивлений известных фаций из третьей библиотеки. Известную геологическую фацию с обучающим распределением пикселов или амплитуд из третьей библиотеки, которое наиболее близко согласуется с распределением пикселов или распределением амплитуд данного сегмента, определяют в качестве результата промежуточной классификации этого сегмента на основании распределения данных этого свойства (см. действие 635) или фаций, указанных для этого сегмента распределением данных этого свойства. Хотя меры подобия определяют с помощью хи-квадрат статистики, предполагается, что другие статистики можно использовать в других осуществлениях изобретения. В случае равномерной сегментации с неперекрывающимися интервалами дополнительные проверки могут быть выполнены для уточнения границ сегментов. Эти проверки могут включать в себя нахождение наилучших согласований для однофутовых (30,48 см) сегментов в пределах более крупных сегментов постоянной длины и сдвиг границ, если однофутовый (30,48 см) сегмент после границы согласуется с той же самой фацией, что и прилегающий, более крупный сегмент. В осуществлении извлечение признаков из распределений вейвлет-коэффициентов, выполняемых под углом к оси буровой скважины, производят аналогичным образом. После того как фации, указанные всеми рассмотренными распределениями, определены для каждого сегмента, эту информацию используют для выполнения конечного определения фации каждого сегмента. Этот процесс, который в дальнейшем может называться этапом слияния признаков, применяют для каждого сегмента в буровой скважине. Процесс слияния признаков включает в себя правила, которые точно определяют, какие фации должны идентифицироваться в качестве конечного результата для сегмента. Сегмент характеризуется определенными флагами признаков и фациями k1, k2 kn, указанными распределением признаков (измеренных свойств или вычисленных/производных величин) d1, d2 dn соответственно, где d1, d2 dn представляют собой, например, измеренные или производные скважинные данные (например, в третьей библиотеке) или коэффициенты вейвлет-преобразования различных измеренных свойств или производных величин при разных масштабах (то есть составляющих первую и вторую библиотеки) из вейвлетпреобразования, выполняемого вдоль оси буровой скважины или вдоль другого направления. Правила основаны на распознавающих классах всех фаций, которые удовлетворяют некоторому свойству класса,определяемому на основании указанных фаций k1', k2' kn' из репрезентативных образцов фаций с распределениями признаков d1, d2 dn соответственно, и на основании их флагов признаков. Флаг признака сегмента определяют для конкретного свойства (признака) p1 и он является значимым, если это свойство изменяется существенно при измерении вокруг оси буровой скважины в том же самом сегменте. В случае, когда p1 представляет данные об удельном сопротивлении от многоконтактного зонда или вейвлет-преобразование таких данных, флаг признака p1 показывает, что распределениеp1 изменяется значительно от одного измерительного башмака к другому как свидетельство того, что фации, согласованные с образцами от различных измерительных башмаков в сегменте при промежуточной классификации на основании признака p1, в соответствии с некоторым правилом являются существенно различающимися. В этой связи правило, по которому точно определяют существенно различающиеся фации, можно разработать для конкретной обстановки осадконакопления. Наличие таких различных изображений с измерительных башмаков в одном и том же сегменте до некоторой степени указывает на фации других, разрывных типов. Например, в обстановке осадконакопления в мелком море согласно изобретению один из флагов признаков вычисляют следующим образом на основании изменчивости от измерительного башмака к измерительному башмаку распределения вейвлет-коэффициентов удельного сопротивления в масштабе 1/8 фута (3,81 см), вычисленного для отдельных измерительных башмаков. Во-первых, выполняют сравнение распределения вейвлет-коэффициентов в масштабе 1/8 фута (3,81 см) для каждого измерительного башмака и распределения вейвлет-коэффициентов в масштабе 1/8 фута (3,81 см) для обучающих образцов фаций. Фация, указанная для данного измерительного башмака распределением вейвлеткоэффициентов удельного сопротивления в масштабе 1/8 фута (3,81 см) (или в результате сравнения с ним), является фацией с наилучшей мерой подобия. Кроме того, результат сравнения является строго подтвержденным, если соответствующая хи-квадрат вероятность выше, чем определенное пороговое значение, например 50%. Во-вторых, если существуют два измерительных башмака, с которых имеются строгие результаты сравнения, которые представляют собой фацию, несовместимую с существованием единственной непрерывной фации на протяжении буровой скважины согласно правилу существенно отличающейся фации, то флаг фации указывает на разрывную фацию. Существенно отличающиеся фации для условий мелкого моря представляют собой любые однородные фации, наблюдаемые на одном измерительном башмаке, и толстослойные фации на другом измерительном башмаке. Эту процедуру можно распространить на требование отсутствия строгого результата сравнения для меры не самого высокого подобия (не самого лучшего по строгости согласования), исключая слоистые и хаотические фации на измерительных башмаках, согласованных со слоистыми фациями. Свойство класса, определяемое на основании фаций при наличии репрезентативных обучающих образцов, для которых имеются результаты сравнения, k1, k2 kn, при наличии распределений признаков d1, d2 dn соответственно, и на основании флага признака p1, представляет собой такое свойство,при котором этот класс содержит все фации, которые могут иметь упорядоченный (n+1)-элементный кортеж (k1, k2 kn, р 1-флаг), принадлежащий к прямому произведению (S1S2SnSp1) из поднаборов S1 Sn, Sp1, так что k1 может принадлежать к поднабору S1 всех фаций, тогда как k2 принадлежит к поднабору S2 фаций и т.д., так что kn принадлежит к поднабору Sn фаций, и такое свойство, что флаг признака p1 указывает на поднабор фаций, то есть принадлежность к поднабору Sp1 фаций, и такое свойство, что все фации по меньшей мере в одном поднаборе входят в соответствующие результаты сравнения репрезентативных образцов для каждой из фаций в этом классе. Последняя деталь означает исключение избыточности из определения класса, так что: 1) только те фации могут быть в одном и том же классе, репрезентативные образцы которых имеют аналогичный образ с учетом фаций, указанных для них распределением определенных признаков, и 2) набор фаций, которые принадлежат к одному классу,не является объединением двух или большего количества поднаборов фаций, которые не просто удовлетворяют свойству класса, а более ограниченному свойству фаций, указанных тем же распределением признаков, которое было использовано для определения исходного класса. Репрезентативные образцы фаций означают такие образцы фаций, которые могут быть удовлетворительно описаны экспертом для представления этих фаций. Этим гарантируется, что резко отклоняющиеся значения (а также образцы,полученные путем принятия "двойственного решения"), отбрасываются, а разброс результатов сравнения, которые могут быть получены по репрезентативным образцам, является небольшим. Классом, фации которого наблюдаются только в случае описанных результатов сравнения в виде свойства класса,поддерживается способ исключающего обоснования, который описан ниже на этапе (с) слияния признаков и показан на примере обстановки глубинного слоистого осадконакопления класса С. Такой класс можно назвать классом включений. Свойство класса и знание всех фаций, которые принадлежат к этому классу, являются полезными для идентификации поднабора фаций, к которому принадлежит фация данного сегмента, если фация, указанная для этого сегмента, является согласованной со свойством этого класса. В случае класса с фациями единственного вида его компонентная фация m может идентифицироваться соответствующим свойством класса. Если соответствующее свойство класса основано на фации,указанной распределением только одного признака d, эта фация m может идентифицироваться распределением признака d. В обстановке глубинного осадконакопления, например, с семью фациями правила согласно осуществлению изобретения основаны на отбрасывании различных классов, показанных на фиг. 7 а и 7b. Правила основаны на отбрасывании следующих классов:(i) одноэлементного класса Cm, состоящего из всех фаций, которые удовлетворяют свойству, заключающемуся в том, что результат k1 сравнения их репрезентативных образцов вместе с распределением данных об удельном сопротивлении может указывать на эти конкретные фации m, то есть k1=m; эти классы обозначены как С 1, С 5, С 6, С 8 и С 11 согласно некоторому количеству соответствующих компонентных фаций, а классы С 1 и С 5 представляют собой классы включений, описанные выше;(ii) двухэлементного класса Cwc из всех фаций, которые удовлетворяют свойству, заключающемуся в том, что результаты сравнения, k1, k2 и k3, их репрезентативных образцов вместе с распределениями данных об удельном сопротивлении и распределениями коэффициентов вейвлет-преобразования удельного сопротивления в масштабе 1/8 фута (3,81 см) и в масштабе 1/16 фута (1,905 см) из данных об удельном сопротивлении соответственно могут указывать на фации 7 или 10; этот класс состоит из фаций 7 и 10 и представляет собой класс включений, описанный выше (то есть только для репрезентативных образцов этих двух фаций имеются эти результаты сравнения);(iii) одноэлементного класса Cm2 из всех фаций, для репрезентативных образцов которых могут иметься результаты k1=7 и k2=m сравнения, при этом m=6, 7, 8 или 10 соответственно для Cm2, вместе с распределением данных об удельном сопротивлении и распределением коэффициентов вейвлетпреобразования в масштабе 1/8 фута (3,81 см) соответственно; этими классами являются С 62, С 72,С 82 и С 102, названные согласно некоторому количеству соответствующих компонентных фаций, а класс С 72 представляет собой класс включений;(iv) одноэлементного класса C11-прим, состоящего из всех фаций, для репрезентативных образцов которых могут иметься результаты k1, например 7, и k2 сравнения, принадлежащие к поднабору 1, 5,11, вместе с распределением данных об удельном сопротивлении и распределением коэффициентов вейвлет-преобразования удельного сопротивления в масштабе 1/8 фута (3,81 см) соответственно; этот класс состоит из фаций 11;(v) трехэлементного класса С 3, состоящего из всех фаций, для репрезентативных образцов которых могут иметься фации k1=10, указанные распределением данных об удельном сопротивлении; этот класс состоит из фаций 10, 8 и 6;(vi) одноэлементного класса С-последний, состоящего из всех фаций, для репрезентативных образцов которых могут иметься результаты сравнения, k1=10, k2, принадлежащие к фациям 1, 5, 6 или 7, иk3, принадлежащий к фациям 1, 5 или 6, при этом k1, k2 и k3 указываются распределениями данных об удельном сопротивлении и их коэффициентами вейвлет-преобразования в масштабе 1/8 фута (3,81 см) и 1/16 фута (1,905 см) соответственно; этот класс состоит из фаций 6. В осуществлении правила точно определяют конечную идентификацию фаций, основанную на согласовании фаций, указанных для данного сегмента, со свойствами, в соответствии с которыми определяются различные классы и уменьшается количество фаций, для репрезентативных образцов которых могут иметься те же указанные фации, что и для данного сегмента. Сначала выбирают первичное свойство распределения признака d1, такого как распределение данных об удельном сопротивлении, при условии, что результаты сравнения точно определены в свойствах всех или почти всех классов и большое количество классов может идентифицироваться этим распределением. Следующим наилучшим кандидатом на такое свойство можно назвать вторичное свойство. Для каждого данного сегмента правила точно определяют конечную идентификацию фаций, которую выполняют следующим образом:(a) определяют, какие поднаборы S1 фаций k1, указанных для данного сегмента распределением d1,принадлежат ко всем поднаборам, обозначающимся в свойствах фаций, указанных распределением d1(для репрезентативных образцов), использованным для определения классов; для каждого такого поднабора S1 идентифицируют класс С 1 так, что для репрезентативных образцов их фаций могут иметься ре- 10019763 зультаты сравнения вместе с распределением признака d1, принадлежащего к S1, и при этом все фации вS1 указываются репрезентативными образцами каждой из фаций в С 1;(b) если при выполнении (а) обнаруживаются одноэлементные классы среди всех классов С 1, то: (i) если имеется одноэлементный класс, определяемый единственным свойством, так что результат сравнения репрезентативных образцов фаций с распределением d1 может принадлежать к поднабору, содержащему k1, то элемент этого класса является фацией, определяемой в качестве результата конечной классификации для этого сегмента; (ii) если одноэлементный класс с наименьшим количеством распределений, необходимых для определения свойства класса, также определяется другими признаками d2 dn, и к тому же, возможно, флагами признаков, то: 1) если другие результаты сравнения относительно этого сегмента, k2 kn, вместе с d2 dn соответственно (и флагами признаков), согласуются со свойством этого класса, то элемент этого класса представляет собой фацию, которая соответствует этому сегменту; 2) если другие результаты сравнения относительно данного сегмента согласуются с этим классом, одноэлементный класс со следующим наименьшим количеством определяющих свойства распределений рассматривают аналогичным образом; 3) если имеются несколько одноэлементных классов с тем же количеством определяющих свойства признаков, то эти классы рассматривают в некотором выбираемом порядке важности;(c) если нет одноэлементных классов среди классов С 1 фаций, которые удовлетворяют тому, что их репрезентативные образцы могут иметь результат сравнения вместе с распределением признака d1, согласованным с данным сегментом, следующие наименьшие классы рассматривают в порядке, аналогичном порядку, установленному в (b), и используют способ исключения этих фаций из класса, который принадлежит к другим классам (и сначала рассматривают классы включений), так что репрезентативные образцы фаций в этих других классах имеют результаты сравнения, которые не согласуются с этим данным сегментом;(d) когда все указанные фации и флаги признаков согласуются со свойствами репрезентативных образцов более чем одной фации, то используют правило возврата к исходному. В осуществлении правилом возврата к исходному в критерии включается выбор фации, которая дается результатом сравнения распределения первичного признака, если этим признаком выделяются эти фации, или следующего признака, выбираемого в порядке важности на этапе (b)(ii)(3);(e) если при запросе на этапе (а) в результатах классы С 1 не обнаружены, фации k2, указанные вторичным признаком d2, рассматривают тем же способом, как в случае, когда k1 было предназначено для первичного распределения, и выполняют этапы (а)-(d); итерацию (е) можно выполнять до тех пор, пока не будет обнаружена фация с результатами сравнения, согласованными с результатами относительно данного сегмента, или до тех пор, пока не будут исчерпаны все признаки, используемые для классификации при исследовании классов С 1 для выбранного признака, и в этом случае (f) используют правило возврата к исходному, в соответствии с которым сегменту приписывается фация, указанная первичным распределением признака. Если фации, указанные всеми рассмотренными распределениями (например, распределениями удельного сопротивления и вейвлет-коэффициентов при различных масштабах, полученными из первой,второй и третьей библиотек обучающих образцов), всегда были одними и теми же фациями, то не будет ничего нового для составления заключения на основании распределений вейвлет-коэффициентов, и промежуточная классификация, основанная на измеренных данных, будет конечной классификацией (если не используют несколько измеренных свойств и вычисленных величин (помимо вейвлетпреобразования. Однако в случае неоднородных фаций с резко выраженными текстурами, видимыми на изображениях удельного сопротивления или в других данных, вейвлет-коэффициентами этих данных предоставляется информация, которая часто отсутствует в распределениях измеренных данных. На фиг. 8 показано применение способа слияния признаков и конечной классификации (a-f) согласно осуществлению изобретения. В этом применении распределение первичного свойства (на этапе (а представляет собой распределение данных изображений удельного сопротивления. Как показано на фиг. 8, способ выполнения слияния признаков и конечной классификации начинают с действия 815, при этом сначала определяют, указывает ли распределение скважинных данных (например, пикселов изображения или амплитуд сигнала) на наилучшее согласование (известной геологической фации) с одной из фаций,однозначно различаемой по распределению удельного сопротивления (или в соответствии с этапом (b)(i), фаций, которые являются членами класса с фациями одного вида, при этом свойство класса основано только на распределении удельного сопротивления). Если результат этого исследования 815 является оправдывающим ожидание (да), сегмент классифицируют (действие 820) только в соответствии с распределением скважинных данных (например, распределением пикселов). Если результат этого исследования является не оправдывающим ожидание (нет), распределение скважинных данных (например, распределение пикселов) указывает на фацию 7 или 10 (на необходимость действия 835 или 850), и при последующих исследованиях также используют распределения вейвлет-коэффициентов для определения правильного класса. Поэтому в этом случае могут быть необходимы этапы (b)(ii) и (c)-(f). В способе переходят к действию 835, при этом выполняют исследование относительно того, указывает ли наилучшим образом согласованное распределение скважинных данных (например, распределе- 11019763 ние пикселов) на фацию 7. Если результат исследования 835 является оправдывающим ожидание (да),выполняют исследование относительно того, указывают ли коэффициенты вейвлет-распределения в масштабе 1/8 фута (3,81 см) на фацию 7 (действие 840). Если результат исследования 840 является оправдывающим ожидание (да), в способе переходят к действию 830, при выполнении которого фацию 7 выбирают для данного сегмента. Этот выбор иллюстрируется применением этапа (b)(ii)(1), и при этом используют свойство класса для класса С 72 на фиг. 7. Если результат исследования 840 является не оправдывающим ожидание (нет), выполняют другое исследование относительно того, указывает ли распределение вейвлет-коэффициентов в масштабе 1/8 фута (3,81 см) на однородные фации 1, 5 или 11 (действие 841). Если результат этого исследования (действие 841) является оправдывающим ожидание (да),сегмент классифицируют как фацию 11 (действие 842). Этот выбор иллюстрируется применением этапа(b)(ii)(1), и при этом используют свойство класса для класса C11-прим на фиг. 7. Если результат этого исследования является не оправдывающим ожидание (нет), сегмент классифицируют (действие 845) в соответствии с фациями, идентифицированными распределением вейвлет-коэффициентов в масштабе 1/8 фута (3,81 см). В этом случае конечная классификация приводит к результату на основании этапа(b)(ii)(1), применяемого к классу Cm2, где m равно количеству фаций, указанных вейвлеткоэффициентом k2=m в масштабе 1/8 фута (3,81 см). Если результат исследования при выполнении действия 835 является не оправдывающим ожидание(нет), в способе переходят к действию 850, при этом выполняют исследование относительно того, указывает ли распределение скважинных данных (например, распределение пикселов) на фацию 10. Это исследование не является необходимым, если только не возникает желание идентифицировать две фации из фаций, которые не различаются только по одному удельному сопротивлению, поскольку в этот момент действия остается только фация 10 в качестве возможного результата промежуточной классификации на основании распределения данных об удельном сопротивлении. Если результат исследования 850 является не оправдывающим ожидание (нет), действие можно продолжить для запроса всех классов фаций на основании фаций, указанных распределениями вейвлет-коэффициентов, чтобы найти, имеет ли какой-либо класс свойство, согласованное с результатами сравнения относительно этого сегмента, начав с другого первичного распределения, как представлено действиями (а)-(е) (например, начав с распределения вейвлет-коэффициентов масштаба 1/8 фута (3,81 см. Однако, если в случае определенных классов, имеющихся на фиг. 7 а и 7b, такой класс не находится, используют правило возврата к исходному из этапа (f) (действие 851 - правило возврата к исходному). Поэтому, если результат исследования 850 является не оправдывающим ожидание (нет), фацию, указанную измеренным распределением данных (действие 820) выбирают для классификации данного сегмента (в соответствии с правилом 851 возврата к исходному). Если результат исследования 850 является оправдывающим ожидание (да), в способе переходят к действию 855, при выполнении которого выполняют исследование относительно того, указывают ли коэффициенты вейвлет-распределения в масштабе 1/8 и 1/16 фута (3,81 и 1,905 см) на фацию 7 или 10. Если результат исследования 855 является оправдывающим ожидание (да), фацию 10 выбирают (действие 860) в качестве конечного результата. Она является результатом способа исключения на этапе (с),примененного к классу Cwc для исключения фации 7 из класса С 72. Если результат исследования 855 является не оправдывающим ожидание (нет), выполняют (действие 856) другое исследование для определения, указывают ли распределения вейвлет-коэффициентов в масштабе 1/8 фута (3,81 см) и 1/16 фута(1,905 см) на одну из фаций 1, 5, 6 или 7, а распределение вейвлет-коэффициентов в масштабе 1/16 фута(1,905 см) не указывает на фацию 7. Если результат этого исследования (действие 856) является оправдывающим ожидание (да), выбирают (действие 857) фацию 6. Она является результатом этапа (b)(ii)(1),примененного к классу С-последний. Если результат является не оправдывающим ожидание (нет), выбирают (действие 858) фацию 8. Последняя является результатом способа исключения на этапе (с), примененного к классу С 3 для исключения фации 6 из класса С-последний и фации 10 из класса Cwc. Когда необходимо более детальное различение фаций со сложной структурой, может быть желательным включение распределений коэффициентов из вейвлет-преобразования, выполненного под углом к оси буровой скважины. В этом случае слияние признаков может быть более сложным, но концептуально понятным; конечная классификация в случае гистограммы пикселов с промежуточным средним может зависеть от гистограмм вейвлет-коэффициентов и может приниматься во внимание уровень определенности (выраженный через меру подобия) на основании преобразований при нескольких углах. Если получают хорошее согласование только при одном угле (например, 5), то имеется вероятность существования фаций с направленным порядком. Если хорошее согласование получают при небольшом количестве углов, результат может быть связан с плохо упорядоченными фациями. Теперь обратимся к фиг. 9 и 10, поскольку на них более широко иллюстрируется способ слияния признаков и конечной классификации (a)-(f) и образования правил. На фиг. 9 первое действие 905 при образовании правил состоит из нахождения одного измеренного или вычисленного свойства, которое можно назвать первичным признаком, распределение которого само идентифицирует каждую фацию из большого набора или поднабора фаций, используемых для обучения. Если имеются несколько таких распределений, то одно, которое обнаруживается в свойствах большей части классов, выбирают (действие 910) в соответствии с этапом (а) слияния признаков. Следующие два действия при формировании правил являются действиями 915 и 920 из фиг. 9. При выполнении действия 915 определяют масштаб c1, с 2 cn характеристической длины пространственной изменчивости данных на основании обучающих образцов тех фаций, которые не идентифицируются только одним распределением d1 (здесь n является количеством таких фаций). При выполнении действия 920 определяют масштаб wj из масштабов, используемых при вычислении вейвлет-преобразования, который является наиболее близким к масштабу cj характеристической длины для каждого j=1, 2 n (действие 925) из масштабов длины, которые находят при выполнении действия 915. После проверки, аналогичной проверке при выполнении действия 905 из фиг. 9, находят упорядоченные пары фаций k1 и k2j, указанные для репрезентативных образцов распределением d1 и соответствующим распределением вейвлет-коэффициентов в масштабе wj соответственно (действие 925), и в способе переходят к действию 930, при выполнении которого находят идентифицируемые фации. В случае любых (k1, k2j), для которых две или три фации имеют репрезентативные образцы для этих указанных фаций, это нахождение принимают во внимание при выполнении действия 935, так что можно образовать классы с фациями двух и трех видов со свойством, заключающимся в том, что они содержат все фации вместе с репрезентативными образцами, которые могут иметь соответствующие указанные фации(k1, k2j). Эти классы могут быть полезными для способа исключения в случае отсутствия фаций, идентифицируемых упорядоченной парой, тройкой и т.д. до n-элементного кортежа указанных фаций для данного сегмента с различными распределениями признаков. Если нет фаций, идентифицируемых упорядоченной парой фаций (k1, k2), указанных для данного сегмента любыми двумя распределениями, в способе переходят к действию 940 из фиг. 9, при выполнении которого фации идентифицируют, исходя из троек, четверок и т.д. до n-элементных кортежей указанных фаций, основываясь на правилах, которые образованы при выполнении действия 940 из фиг. 9,аналогично действию 930. Это представляет собой этап (b)(ii)(2) слияния признаков. Фацию, которая обычно является связанной (и поэтому идентифицируется) при наличии определенного упорядоченного n-элементного кортежа фаций, указанных распределениями заданных измеренных или вычисленных (включая вейвлет-преобразованных) величин или указанных флагами признаков,находят по ее наиболее высокой вероятности появления по сравнению с другой фацией в результатах ручной классификации по некоторому тестовому набору репрезентативных образцов, которые имеют этот определенный упорядоченный n-элементный кортеж фаций, указанных распределениями этих заданных измеренных или вычисленных величин или флагами признаков. Кроме того, способ исключения из классов, определенных при выполнении действия 935 из фиг. 9, можно проследить в действии 945 и применить в действии 1055 из фиг. 10, и, наконец, правило возврата к исходному определяют при выполнении действия 950 и применяют при выполнении действия 1065 из фиг. 10. В способе на фиг. 10 действие 1005 состоит из точного определения фации для данного сегмента на основании фации, указанной первичным распределением свойства сегмента, если указанная фация принадлежит к большому набору или поднабору фаций, идентифицируемых этим одним распределением. В случае, когда идентифицированные и указанные фации являются одними и теми же, это соответствует этапу (b)(i) слияния признаков. Если результат исследования является оправдывающим ожидание (да),фацию, идентифицированную распределением d1, выбирают (действие 1010) в качестве конечного результата. Если результат исследования является не оправдывающим ожидание (нет), в способе переходят к действию 1020. Действие 1020 (фиг. 10) соответствует действию 930 (фиг. 9): правилами точно определяется фацияk2 для данного сегмента на основании фации k1, указанной первичным распределением признака этого сегмента, и фаций k2j (для каждого j=1 n), указанных соответствующим распределением вейвлеткоэффициентов в масштабе wj, если фация k2 может идентифицироваться упорядоченной парой указанных фаций (k1, k2j) с помощью этих распределений, а фация, указанная первичным распределением признака, не принадлежит к большому набору или поднабору фаций, идентифицируемых этим одним распределением. Действие 1020 из фиг. 10 представляет собой реализацию этапа (b)(ii)(1) слияния признаков при наличии двух распределений. Если результат исследования является оправдывающим ожидание(да), фацию, идентифицированную как k2, выбирают (действие 1025) в качестве конечного результата. Если результат исследования является не оправдывающим ожидание (нет), в способе переходят к действию 1040. При выполнении действия 1040 определяют, имеется ли единственная фация k, идентифицируемая упорядоченным m-элементным кортежем (k1, k2 km) фаций, указанных относительно данного сегмента распределением d1 и некоторыми другими распределениями признаков, при этом k1 не поддается идентификации только с помощью d1 и нет фации, идентифицируемой упорядоченной парой фаций, указанных d1 и любым другим распределением. Если результат исследования является оправдывающим ожидание (да), фацию к выбирают (действие 1045) в качестве конечного результата. Если результат исследования является не оправдывающим ожидание (нет), в способе переходят к действию 1055, при этом определяют, имеются ли результаты сравнения относительно данного сегмента, согласующиеся со свойствами классов из некоторых классов включений с фациями двух или трех типов. Если результат исследования является оправдывающим ожидание (да), способ исключения используют (действие 1060) для идентификации конечного результата. Если результат исследования является отрицательным, используют (действие 1065) правило возврата к исходному. Извлечение признаков и слияние признаков согласно осуществлению изобретения, показанные на фиг. 1, 6 и 7, были проверены на части реальных скважинных данных (520, показанных в столбце 4 на фиг. 5 а и 5b) удельного сопротивления, полученных прибором OBMI (формирователем микроизображений при наличии бурового раствора на нефтяной основе). Очень хорошие результаты были получены в этом случае. Результаты предварительной проверки показали процент результативности около 80% на 50 образцах, примерно равномерно распределенных по семи фациям, за исключением только небольшого количества образцов потока массы жидкого ила и песчаника. Правильно и неправильно идентифицированные фации охватывают все фации из этих семи, при этом крайне маловероятно, что такой процент результативности может обуславливаться случайной подборкой или подборкой сильно нарушенных одной или двух фаций. Как отмечалось выше, в столбце 1 из фиг. 5 а показана диаграмма 505 гамма-каротажа; в столбце 3 показана измеренная глубина вдоль ствола буровой скважины и в столбце 4 показаны нормированные трассы удельного сопротивления; в столбце 5 обозначены границы сегментов, полученные на основании алгоритма сегментации; в столбце 6 фиг. 5 а показано удельное сопротивление (то есть гистограмма пикселов) для каждого 1 фута (30,48 см) данных и в столбцах 7-9 показано распределение вейвлеткоэффициентов для масштаба 1/16 фута (1,905 см) для каждых 3 футов (91,44 см) данных в логарифмическом масштабе (столбец 7), каждого 1 фута (30,48 см) данных в логарифмическом масштабе (столбец 8) и каждого 1 фута (30,48 см) данных в линейном масштабе (столбец 9). В столбце 2 на фиг. 5 а показан индекс геологической фации, идентифицированной с помощью ручной интерпретации. В столбце 2 числа, использованные для обозначений фаций, являются такими же,как числа, использованные при описании примера классов, показанных на фиг. 7 а и 7b. Теперь обратимся к столбцам 13-16 фиг. 5, где в этих столбцах показаны результаты промежуточной классификации, которые получены в соответствии со способом, показанным на фиг. 6. Эти результаты определены в виде кода фации, деленного на 10, и соответствующих мер подобия, при этом в столбце 13 код фации (деленный на 10) показан для удельного сопротивления, в столбце 14 для вейвлеткоэффициентов в масштабах 1/32, 1/16 и 1/8 фута (0,9525; 1,905 и 3,81 см). В столбцах 15 и 16 показаны вероятности (Q(2,v в согласовании с масштабом 1/16 фута (1,905 см) и масштабом 1/8 фута (3,81 см) соответственно, распределений вейвлет-коэффициентов для обучающих образцов фаций. Как отмечалось выше, столбцы 17-20 из фиг. 5 а аналогичны столбцам 13-16, но отличаются тем,что обучающий образец для фации 8 является другим. Как показано на фиг. 5 а, отображенные вероятности в столбцах 19 и 20 являются такими же, как в столбцах 15 и 16 соответственно, за исключением вероятностей согласования с обучающим образцом фации 8 (например, в области ниже 500 футов (152 м) на этом чертеже). Столбцы с 21 по 23 на фиг. 5 а аналогичны столбцам 17-19 соответственно (при одинаковых обучающих образцах), за исключением того, что большие сегменты не разделены на блоки по 3 фута (0,9144 см). В отличие от столбцов 13 и 17 в столбце 21 изменение отсутствует ниже 519 футов (158,1912 м). Репрезентативные тестовые сегменты и конечные фации, определенные на этом участке каротажной диаграммы изображений на основании результатов промежуточной классификации в столбцах 13-14 на фиг. 5, показаны в таблице. Из всех сегментов, полученных обычной сегментацией, репрезентативные тестовые сегменты представляют собой только те, которые полностью находятся в пределах сегментов геологических фаций (столбец 2 на фиг. 5) и не имеют поперечных синусоидальных границ толстых слоев на изображении прибора OBMI (формирователя микроизображений при наличии бурового раствора на нефтяной основе) из столбца 4. Таким образом выполнена оценка точности классификации. В таблице также показано сравнение результатов классификации, полученных способом согласно осуществлению изобретения, и результатов классификации, полученных ручной классификацией изображений и показанных в столбце 2 фиг. 5 а и 5b. В таблице показано хорошее совпадение, около 80%, между фациями, найденными автоматизированным способом, и вручную интерпретированными фациями для сегментов образцов, представляющих интерес. Кроме того, это совпадение было обнаружено при тестировании способа на пятидесяти образцах. Распределения вейвлет-коэффициентов для масштабов 1/16 и 1/8 фута (1,905 и 3,81 см) в столбце 14 на фиг. 5 а указывают на правильный класс для сегмента [505,75-508] [154,1-154,8 м]. Кроме того, следует отметить, что при классификации в случае более крупных сегментов, таких как показанные в столбце 21 на фиг. 5 а, идентифицируется правильный класс для сегмента [513,75-516,75] [156,5-157,5 м]. Хотя изобретение было описано подробно с целью иллюстрации на основании осуществлений, считающихся в настоящее время наиболее практичными или предпочтительными, должно быть понятно, что такие подробности предназначены только для этой цели и что изобретение не ограничено раскрытыми осуществлениями, а наоборот, предполагается охватывающим модификации и эквивалентные структуры,которые находятся в пределах сущности и в объеме прилагаемой формулы изобретения. Например, если в этом изобретении осуществляется обращение к компьютеру, то он может представлять собой компьютер общего назначения, специализированный компьютер, специализированную интегральную схему(ASIC), включающую в себя выполняемые машиной команды и программируемую для выполнения способа, компьютерную установку или сеть или другое подходящее компьютерное устройство. В качестве дополнительного примера должно быть понятно, что в настоящем изобретении предполагается, что в пределах возможного один или несколько признаков из любого осуществления могут быть объединены с одним или несколькими признаками из любого другого осуществления. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Реализуемый с помощью компьютера способ анализа характеристик подземной формации, содержащий этапы, на которых применяют посредством процессора компьютера вейвлет-преобразование к измеренным данным или к производным данным, полученным на основании измеренных данных, или к части их, при этом измеренные данные получены измерением по меньшей мере одного физического параметра на каждом из множества мест в буровой скважине, которая проходит через область подземной формации; выбирают один или несколько масштабов для анализа вейвлет-коэффициентов при каждом масштабе; выполняют сегментацию измеренных или производных данных; вычисляют посредством процессора компьютера распределение вейвлет-коэффициентов для каждого масштаба для одного или нескольких пространственных направлений применения вейвлетпреобразования, для вейвлет-преобразования измеренных или производных данных и для каждого сегмента, который принадлежит к участку, относительно которого было вычислено вейвлетпреобразование; для каждого сегмента анализируют распределение измеренных или производных данных и распределение вейвлет-коэффициентов для каждого масштаба в части их перекрытия с соответствующими распределениями обучающих образцов, чтобы получить геологическую интерпретацию подземной формации. 2. Способ по п.1, в котором обучающие образцы являются представляющими фации, идентифицируемые геологом. 3. Способ по п.1, в котором один или несколько масштабов являются сравнимыми с масштабами длины изменений характеристик измеренных данных. 4. Способ по п.1, дополнительно содержащий повторение выполнения сегментации, вычисление распределения данных и вейвлет-коэффициентов и анализ распределения итерационным методом до удовлетворения заданному условию. 5. Способ по п.1, в котором вейвлет-преобразование применяют к каждой трассе измерений от многотрассового измерительного прибора и распределение вейвлет-коэффициентов вычисляют, собирая вейвлет-коэффициенты из всех трасс. 6. Способ по п.1, в котором измеренные данные или производные данные повторно корректируют после применения вейвлет-преобразования. 7. Способ по п.1, в котором сегментацию данных выполняют, разделяя скважинные каротажные данные на интервалы, по существу, равной длины, которые могут перекрываться на заданной фиксированной длине. 8. Способ по п.1, в котором анализ включает в себя для каждого сегмента и каждого масштаба определение фации, указанной распределением вейвлет-коэффициентов для сегмента и масштаба, в качестве фации, представленной обучающими образцами, чье соответствующее распределение вейвлеткоэффициентов наиболее близко соответствует вычисленному распределению вейвлет-коэффициентов в сегменте. 9. Способ по п.8, в котором соответствие между вычисленным распределением вейвлеткоэффициентов и распределением вейвлет-коэффициентов одного из обучающих образцов основано на мере подобия с использованием статистики хи-квадрат. 10. Способ по п.8, в котором анализ дополнительно включает в себя, для каждого сегмента, определение фаций, указанных распределением измеренных или вычисленных данных в качестве фаций, представленных обучающими образцами, чьи соответствующие распределения данных наиболее близко соответствуют распределению измеренных или производных данных. 11. Способ по п.10, в котором соответствие распределения измеренных или производных данных и распределение данных обучающих образцов основаны на мере подобия с использованием статистики хиквадрат. 12. Способ по п.1, в котором вейвлет-преобразование применяют к каждой трассе многотрассовых данных, а анализ включает в себя группирование многотрассовых данных в группы трасс, которые измеряют в пространственной близости друг к другу вокруг буровой скважины, и для каждого масштаба, каждого сегмента и каждой группы трасс определение фации, указанной распределением вейвлеткоэффициентов для масштаба, сегмента и группы трасс, в качестве фации, представленной обучающими образцами, чье соответствующее распределение вейвлет-коэффициентов при этом масштабе наиболее близко соответствует распределению вейвлет-коэффициентов измеренных или производных данных для данного масштаба, данного сегмента и данной группы трасс, при этом указанные фации из каждой группы распределений трасс из данных и вейвлет-коэффициентов для каждого масштаба для данного сегмента сравнивают, чтобы предположить, что их изменчивость вокруг буровой скважины означает фацию разрывного типа, и если их изменчивость означает фацию разрывного типа, фацию, указанную распределением вейвлет-коэффициентов из всех трасс в сегменте, определяют как разрывную фацию. 13. Способ по п.1, в котором анализ включает в себя выполнение конечной идентификации фации для каждого сегмента путем использования правил, которые точно определяют конечную фацию для сегмента на основании фации, указанной распределением вейвлет-коэффициентов, на основании фации,указанной распределениями измеренных или производных данных или обоих, в котором распределения вейвлет-коэффициентов и распределения измеренных или производных данных вычисляют для сегмента в целом или для групп трасс в этом сегменте. 14. Способ по п.13, в котором правила включают в себя различение множества классов, каждый из которых включает в себя по меньшей мере одну фацию, при этом каждая фация приписана к одному или нескольким классам на основании фаций, указанных распределениями вейвлет-коэффициентов для сегментов при различных масштабах и распределением измеренных или производных данных или обоих. 15. Способ по п.14, в котором правила включают в себя первое определение одного первичного свойства в качестве измеренного или вычисленного свойства, чье распределение само идентифицирует каждую фацию из большого набора или поднабора фаций обучающих образцов. 16. Способ по п.15, в котором правила включают в себя конечную идентификацию фаций для заданного сегмента в качестве фаций, указанных распределением сегмента первичного свойства, если указанная фация принадлежит большому набору или поднабору фаций, идентифицируемых одним первым распределением свойства. 17. Способ по п.16, в котором правила включают в себя идентификацию масштаба wj из масштабов,используемых при вычислении вейвлет-преобразования, который является наиболее близким к масштабуcj характеристической длины (где j=1, 2 n) пространственной изменчивости данных из обучающих образцов, где n является количеством фаций, которые не идентифицируются одним распределением первичного свойства. 18. Способ по п.17, в котором правила включают в себя определении фации k2 для данного сегмента на основании (а) фации k1, указанной первичным распределением признака этого сегмента, и (b) фаций k2j (для каждого j=1 n), указанных соответствующим распределением вейвлет-коэффициентов в масштабе wj, если (i) фация k2 может идентифицироваться упорядоченной парой указанных фаций (k1,k2j), и (ii) фация k1 не принадлежит к большому набору или поднабору фаций, идентифицируемых этим одним распределением первичного свойства. 19. Способ по п.18, в котором правила включают в себя определение конечной фации этого сегмента посредством определения, какая фация наиболее связана с имеющей ту же упорядоченную тройку идентифицированной фацией, как и указанная упорядоченная тройка сегмента фаций (k1, k2j, k3k), указанных (а) распределением первичного свойства, (b) распределением соответствующих вейвлеткоэффициентов в масштабе длины wj, (с) распределением вейвлет-коэффициентов в другом масштабе длины wk соответственно, если фация не является идентифицируемой посредством (i) распределения одного первичного свойства или посредством (ii) упорядоченной пары указанных фаций (k1, k2j) при любом из масштабов wj. 20. Способ по п.1, в котором вейвлет-преобразование представляет собой ортогональное вейвлетпреобразование. 21. Способ по п.20, в котором вейвлет-преобразование представляет собой вейвлет Добеши второго порядка. 22. Способ по п.1, в котором измеряемая физическая величина представляет собой электрический сигнал, а характеристика является удельным сопротивлением или импедансом подземной формации. 23. Способ по п.1, в котором измеряемая физическая величина представляет собой сигнал гаммаизлучения, а характеристика является естественным гамма-излучением подземной формации. 24. Компьютерный носитель информации, имеющий выполняемые машиной команды, при этом команды выполняются машиной для осуществления способа анализа характеристик подземной формации, этот способ содержит применение вейвлет-преобразования к измеренным данным или к производным данным, полученным на основании измеренных данных, или к части их, при этом измеренные данные получены измерением по меньшей мере одного физического параметра на каждом из множества мест в буровой скважине,которая проходит через область подземной формации; выбор одного или нескольких масштабов для анализа вейвлет-коэффициентов при каждом масштабе; выполнение сегментации измеренных или производных данных; вычисление распределения вейвлет-коэффициентов для каждого масштаба для одного или нескольких пространственных направлений применения вейвлет-преобразования, для вейвлет-преобразования измеренных или производных данных и для каждого сегмента, который принадлежит к участку, относительно которого было вычислено вейвлет-преобразование; и для каждого сегмента анализируют распределение измеренных или производных данных и распределение вейвлет-коэффициентов для каждого масштаба в части их перекрытия с соответствующими распределениями обучающих образцов, чтобы получить геологическую интерпретацию подземной формации. Классы для критериев слияния признаков в глубинной обстановке с семью фациями (обозначены фации 1, 5, 6, 8,10, 11) Фиг. 7 а
МПК / Метки
МПК: G01V 11/00
Метки: способ, компьютерный, носитель, характеристик, анализа, информации, формации, подземной
Код ссылки
<a href="https://eas.patents.su/22-19763-sposob-i-kompyuternyjj-nositel-informacii-dlya-analiza-harakteristik-podzemnojj-formacii.html" rel="bookmark" title="База патентов Евразийского Союза">Способ и компьютерный носитель информации для анализа характеристик подземной формации</a>
Предыдущий патент: Укупорочный элемент, препятствующий незаконному вскрытию тары
Следующий патент: Установка для извлечения ценного вещества из суспензии и способ извлечения битума из суспензии воды и нефтеносного песка
Случайный патент: Способ получения фосфатов натрия