Способ и устройство для моделирования имитатора коллектора
Формула / Реферат
1. Способ моделирования имитатора коллектора посредством решения нелинейной S-образной функции F=¦(S), которая выражает свойство S в физической системе подземного коллектора с имеющимся потоком флюида, причем S-образная функция имеет точку перегиба Sc и заранее определенное значение F, к которому сходится ¦(S), способ содержит этапы, на которых:
a) выбирают начальное значение Sn+1 как возможное решение функции ¦(S),
b) применяют итерационный метод Ньютона (Т) к функции ¦(S) в Sn для определения значения следующей итерации Sn+1,
c) определяют, располагается ли Sn+1 с противоположной стороны точки перегиба Sc относительно Sn,
d) задают Sn+1=Sl модифицированной новой оценке, если Sn+1 располагается с противоположной стороны точки перегиба ¦(S) относительно Sn+1,
e) определяют, удовлетворяет ли Sn+1 заранее определенному критерию сходимости,
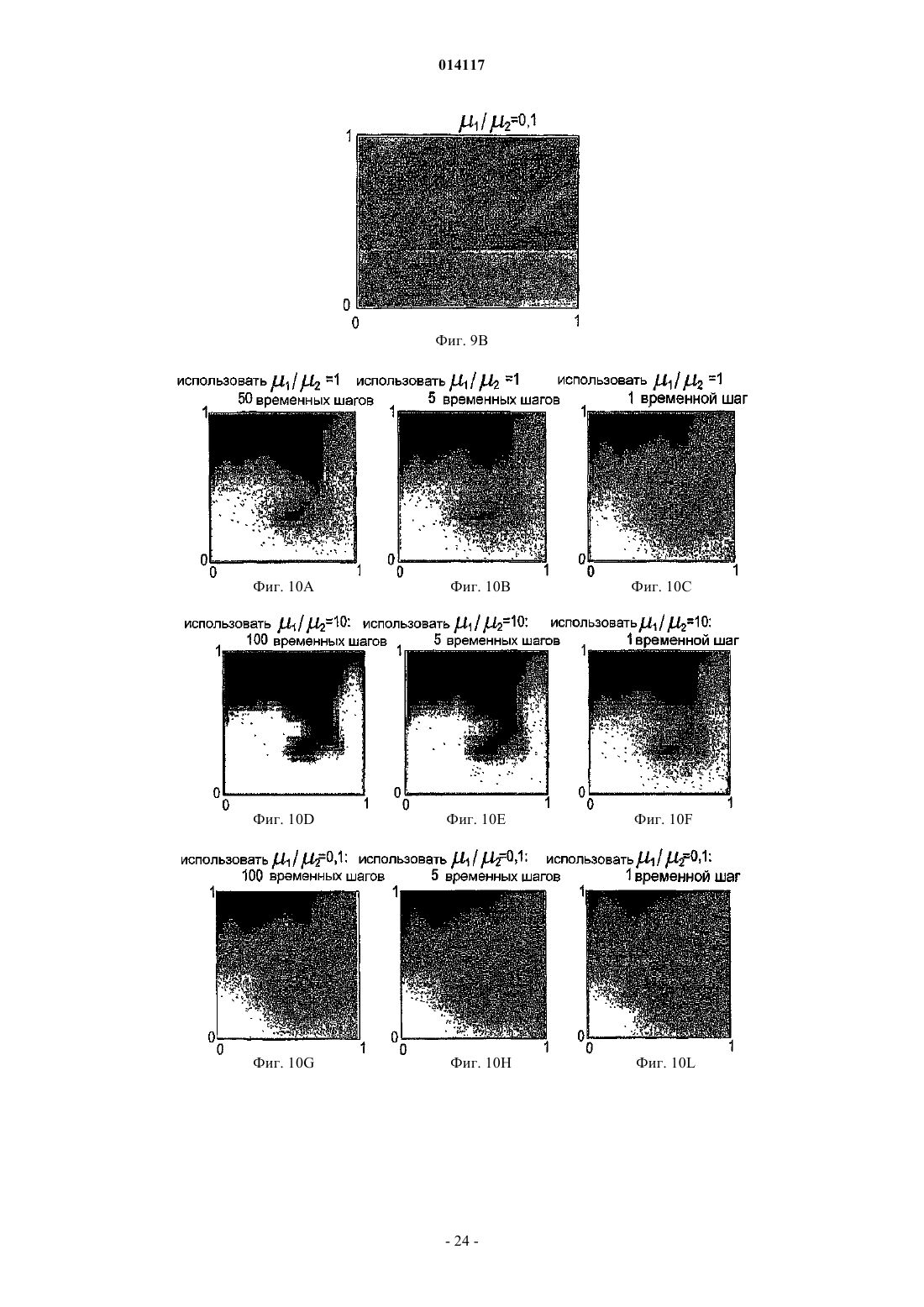
f) задают Sn=Sn+1, если Sn+1 не удовлетворяет заранее определенному критерию сходимости,
g) повторяют этапы (b)-(f), пока Sn+1 не будет удовлетворять заранее определенному критерию сходимости, и
h) выбирают Sn+1 в качестве удовлетворительного решения S для S-образной функции F=¦(S),
i) используют удовлетворительное решение S для S-образной функции ¦(S) для моделирования потока флюида в пределах подземного коллектора посредством имитатора коллектора.
2. Способ по п.1, в котором модифицированную новую оценку Sl задают как Sl=aSn+(1-a)Sn+1, где 0<a<1.
3. Способ по п.2, в котором 0,3<a<0,7.
4. Способ по п.2 или 3, в котором a=0,5.
5. Способ по п.1, в котором модифицированную новую оценку Sl задают равной Sc, точке перегиба функции ¦(S).
6. Способ по любому одному из пп.1-5, в котором S-образная функция ¦(S) является функцией фракционного потока, используемой в имитаторе коллектора для представления характеристик потока флюида в пределах подземного коллектора.
7. Способ по любому одному из пп.1-6, в котором S-образная функция ¦(S) математически согласуется с математическим выражением

где S - насыщенность первой фазы в задаче потока двух флюидов,
¦(S) - функция насыщенности S,
m1 - вязкость флюида в первой фазе и
m2- вязкость флюида во второй фазе.
8. Способ по любому одному из пп.1-7, в котором Sn+1 удовлетворяет заранее определенному критерию сходимости, если
![]()
где e - заранее определенный предел допуска.
9. Способ по любому одному из пп.1-7, в котором Sn+1 удовлетворяет заранее определенному критерию сходимости, если
![]()
где e - заранее определенный предел допуска.
10. Способ по любому одному из пп.1-7, дополнительно содержащий этап, на котором задают Sn+1 равным верхнему или нижнему пределу Sb, если Sn+1 превышает эти пределы на этапе (b).
11. Способ по любому одному из пп.1-10, в котором S-образную функцию F=¦(S) задают посредством одного из поисковой таблицы или общей аналитической функции.
12. Способ по любому одному из пп.1-11, в котором обновляют ньютоновую итерацию, если функция фракционного потока ¦(S) связана с двухфазным потоком в физической системе подземного коллектора с учетом гравитации в ячейке сетки имитатора коллектора, причем обновление отличается тем, что:
(a) проверяют направления фазных скоростей и силы тяжести в ячейке сетки,
(b) если фазные скорости сонаправлены, применяют обычный анализ устойчивости Ньютона,
(i) вычисляют направленные фракционные потоки Fh и Fn и их производные второго порядка (Fh" и Fn"),
(ii) вычисляют Cg для вертикального потока (для горизонтального потока Cg=0),
(iii) применяют предел насыщенности 0£Sn+1£1,
(vi) если Fh''(Sn+1)Fh''(Sn)<0 или Fn"(Sn+1)Fn"(Sn)<0, применяют нижнюю релаксацию для итерации насыщенности,
(c) если фазные скорости противонаправлены,
(i) вычисляют точку отражения насыщенности, Sr*,
(ii) применяют предел насыщенности, если ячейка не соседствует с границей, или соседняя ячейка не принадлежит другой области насыщенности, 0£Sn+1£Sr* или Sr*<Sn+1<1, иначе 0£Sn+1£1,
(iii) если Fh''(Sn+1)Fh''(Sn)<0 или Fn''(Sn+1)Fn''(Sn)<0, применяют нижнюю релаксацию для итерации насыщенности и
d) используют обновленную ньютоновую итерацию для моделирования двухфазного потока флюида в пределах подземного коллектора посредством имитатора коллектора.
13. Способ по любому одному из пп.1-11, в котором обновляют ньютоновую итерацию, если функция фракционного потока ¦(S) связана с трехфазным потоком физической системы подземного коллектора с учетом гравитации в ячейке сетки имитатора коллектора, причем обновление отличается тем, что:
(a) проверяют направления суммарной скорости и силы тяжести,
(b) вычисляют Cg1 и Cg2,
(c) вычисляют границы нулевого фракционного потока для фазы 1, (L1(S1,S2)) и L2(S1,S2),
(d) вычисляют начальные точки для насыщенности, (S1b1,S2b1) и (S1b2,S2b2) на L1(S1,S2) и L2(S1,S2) соответственно,
(e) проверяют знак F1* и F2*,
(f) из первоначальной оценки насыщенностей (S10 и S20) вычисляют оценку фракционного потока (F10 и F20) и детерминант матрицы Якоби,
(g) если F1*³0 и F2*³0,
(i) если первоначальная оценка насыщенностей не удовлетворяет условию положительности, берут точку на L1(S1b1,S2b1) в качестве первоначальной оценки насыщенностей,
(ii) итерируют насыщенности на основании
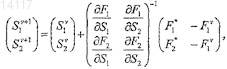
причем после каждой итерации применяется ограничение 0£Sjn+1£1;
(iii) если F1n<0 или F2n<0, задают насыщенность на L1(S1b1,S2b1);
(iv) если S1+S2>1, нормализуют насыщенность, чтобы гарантировать Si³0;
(v) если ![]() или
или ![]() вычисляют нижнюю релаксацию итерации насыщенности,
вычисляют нижнюю релаксацию итерации насыщенности,
(h) если F1*<0, F2*³0 и Det³0, задают первоначальную оценку насыщенностей в точке на L1(S1b1,S2b1);
(i) если F1*<0, F2*³0 и Det<0 или F1*<0, F2*<0 и Det<0, задают первоначальную оценку насыщенностей в точке L1(S1b2,S2b2);
(j) если F1*<0, F2*<0 и F1*<0, F2*<0, задают начальную оценку насыщенности в точке (S1b3,S2b3) и
(k) используют обновленную ньютоновую итерацию для моделирования трехфазного потока флюида в пределах подземного коллектора посредством имитатора коллектора.
14. Устройство для хранения программ, считываемое машиной, материально выполняющее программу, состоящую из команд, выполняемых машиной, для осуществления этапов способа моделирования имитатора коллектора посредством решения нелинейной S-образной функции, F=¦(S), которая выражает свойство S в физической системе подземного коллектора с имеющимся потоком флюида, причем S-образная функция имеет точку перегиба Sc и заранее определенное значение F, к которому сходится ¦(S), способ содержит этапы, на которых:
a) выбирают начальное значение Sn как возможное решение функции ¦(S),
b) применяют итерационный метод Ньютона (Т) к функции ¦(S) в Sn для определения значения следующей итерации Sn+1,
c) определяют, располагается ли Sn+1 с противоположной стороны точки перегиба Sc относительно Sn,
d) задают Sn+1=Sl модифицированной новой оценке, если Sn+1 располагается с противоположной стороны точки перегиба ¦(S) относительно Sn,
e) определяют, удовлетворяет ли Sv+1 заранее определенному критерию сходимости,
f) задают Sn=Sn+1, если Sn+1 не удовлетворяет заранее определенному критерию сходимости,
g) повторяют этапы (b)-(f), пока Sn+1 не будет удовлетворять заранее определенному критерию сходимости,
h) выбирают Sn+1в качестве удовлетворительного решения S-образной функции F=¦(S) и
i) используют удовлетворительное решение S-образной функции ¦(S) для моделирования потока флюида в пределах подземного коллектора посредством машины.
Текст
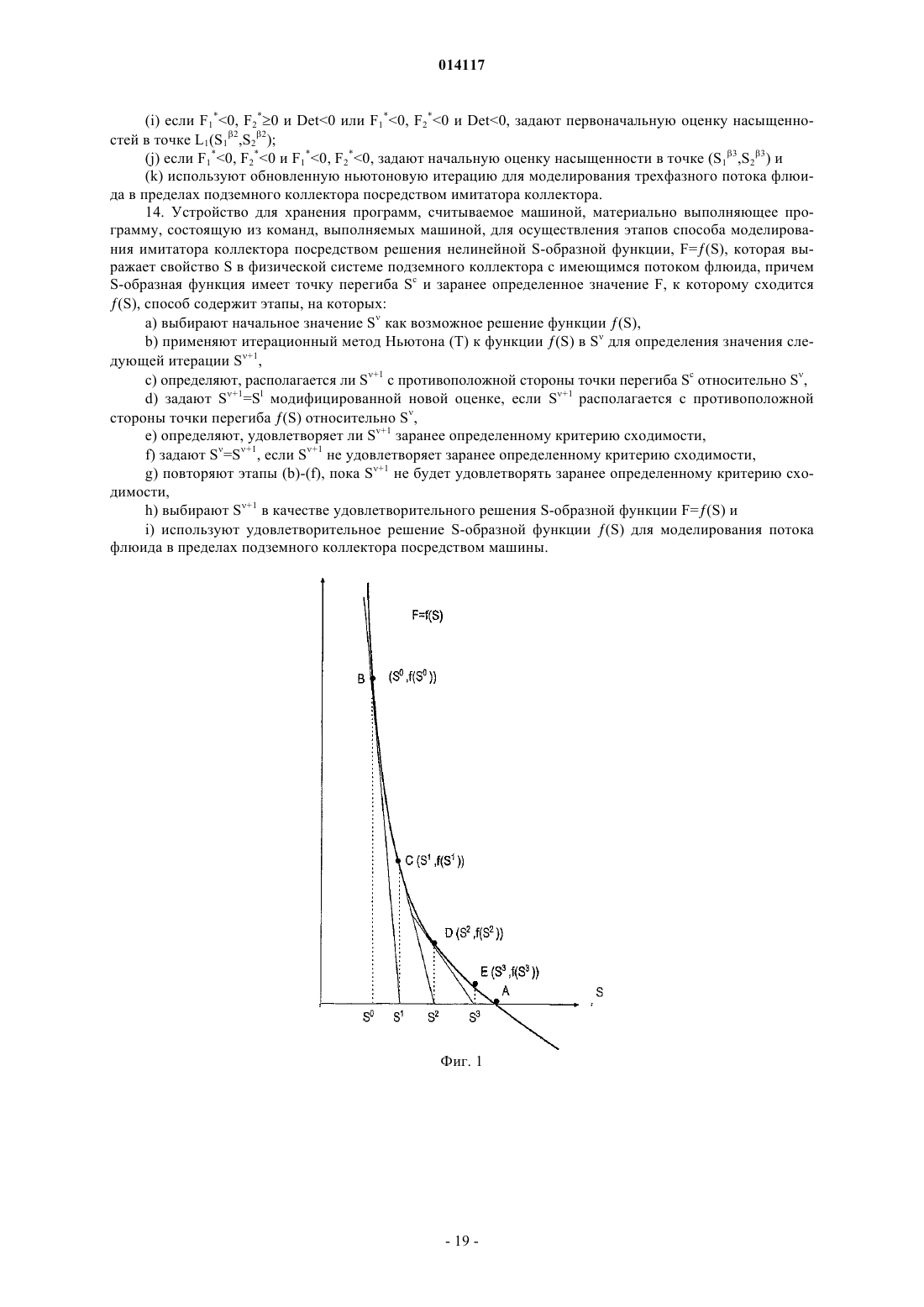
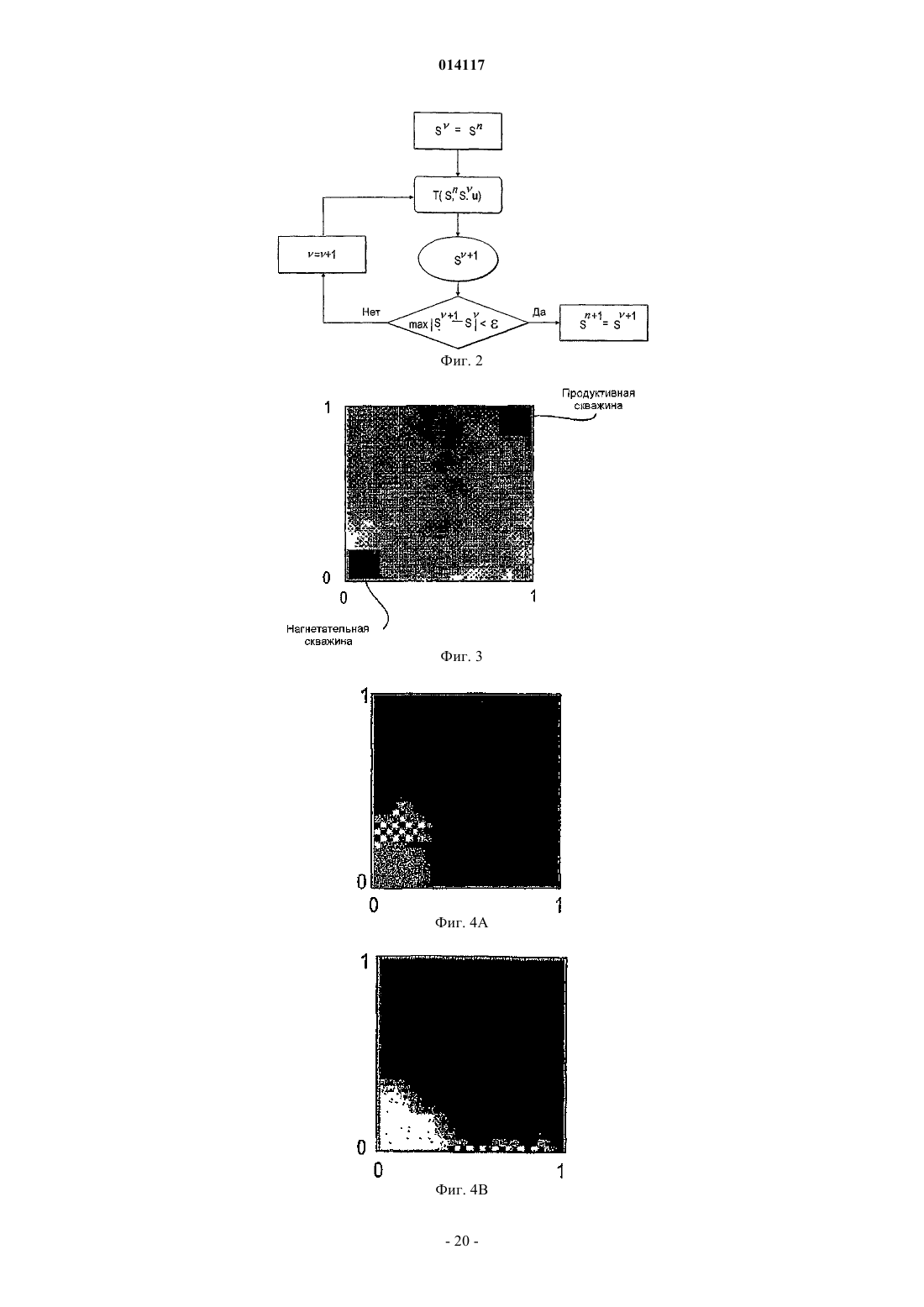
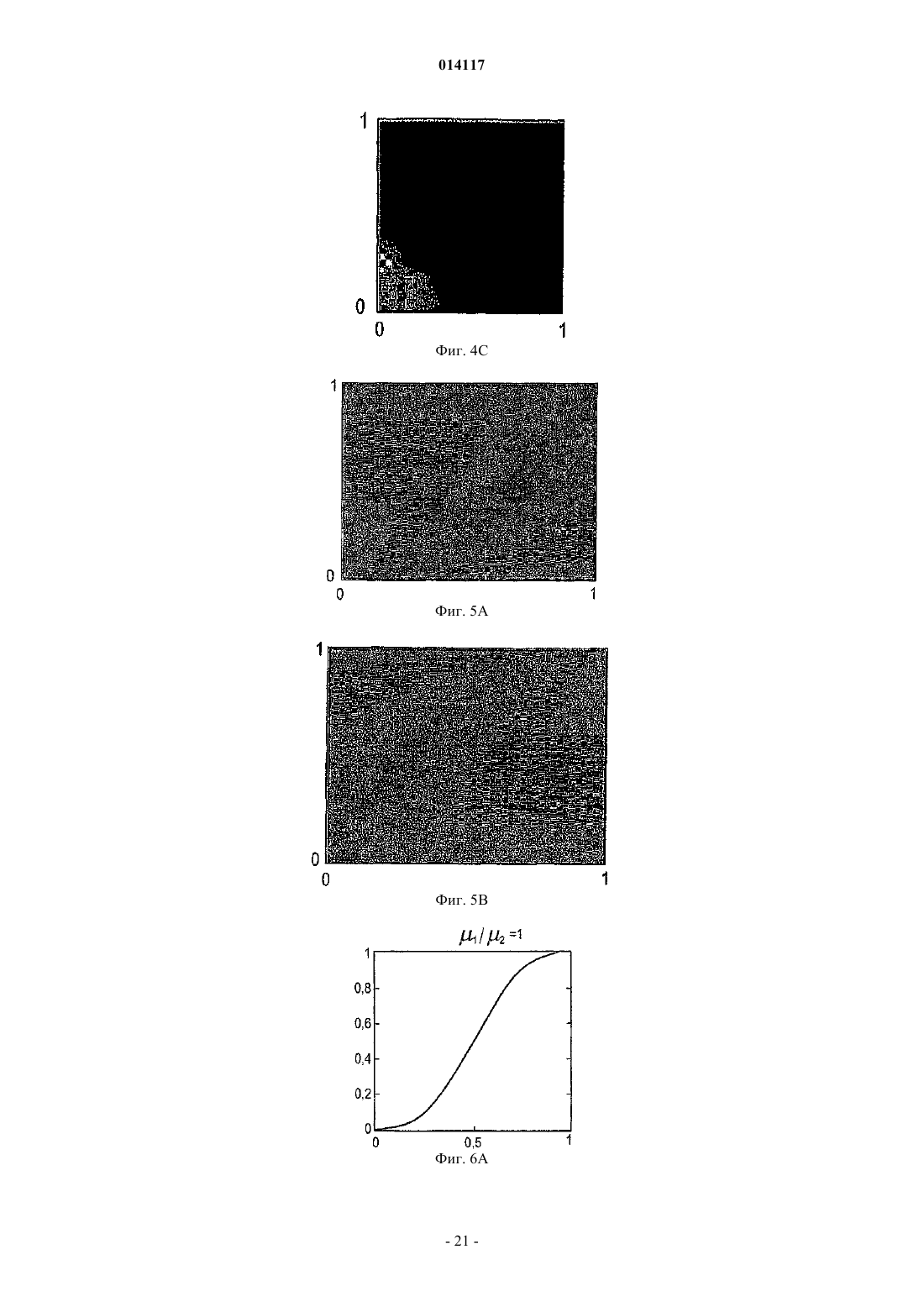
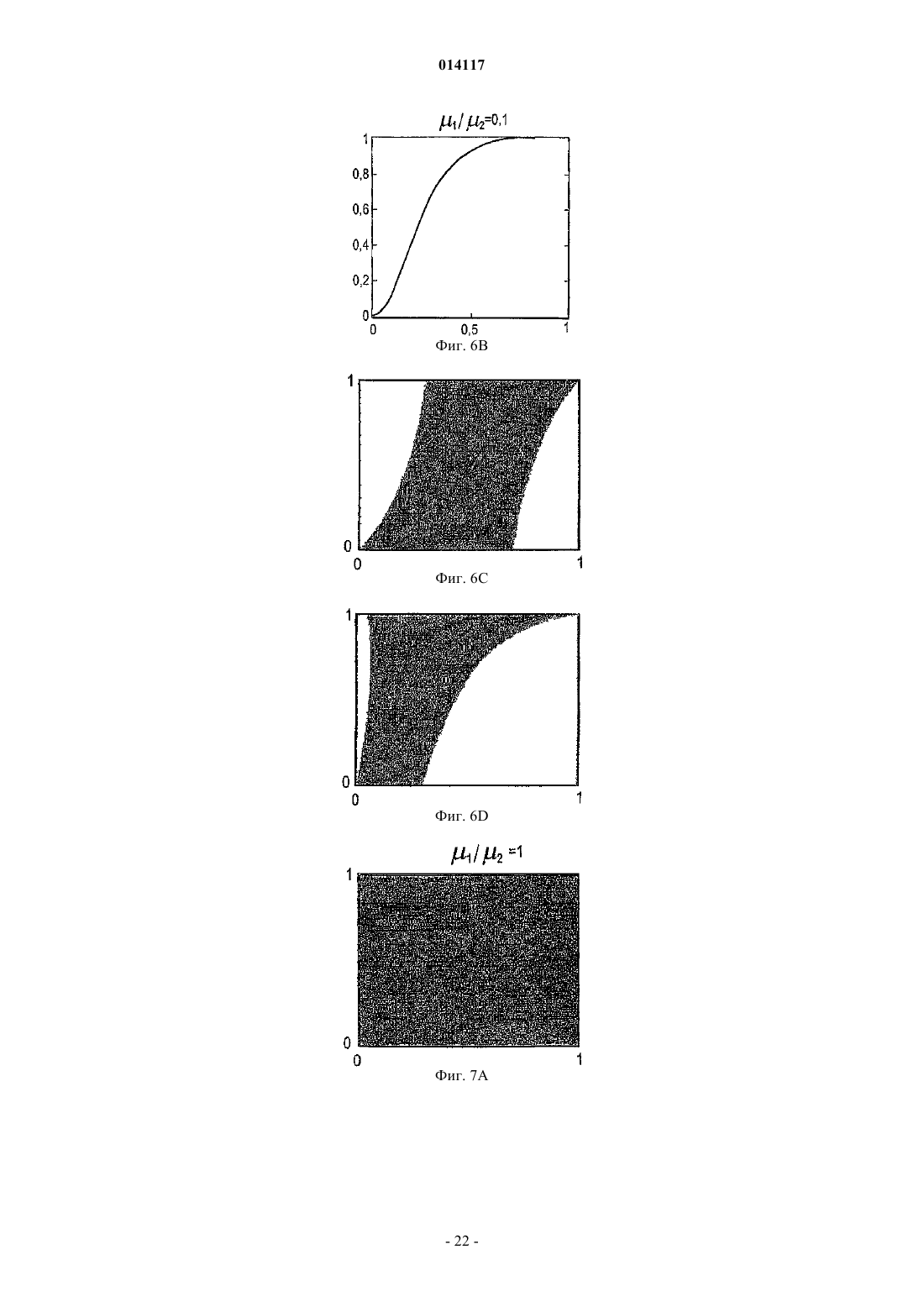
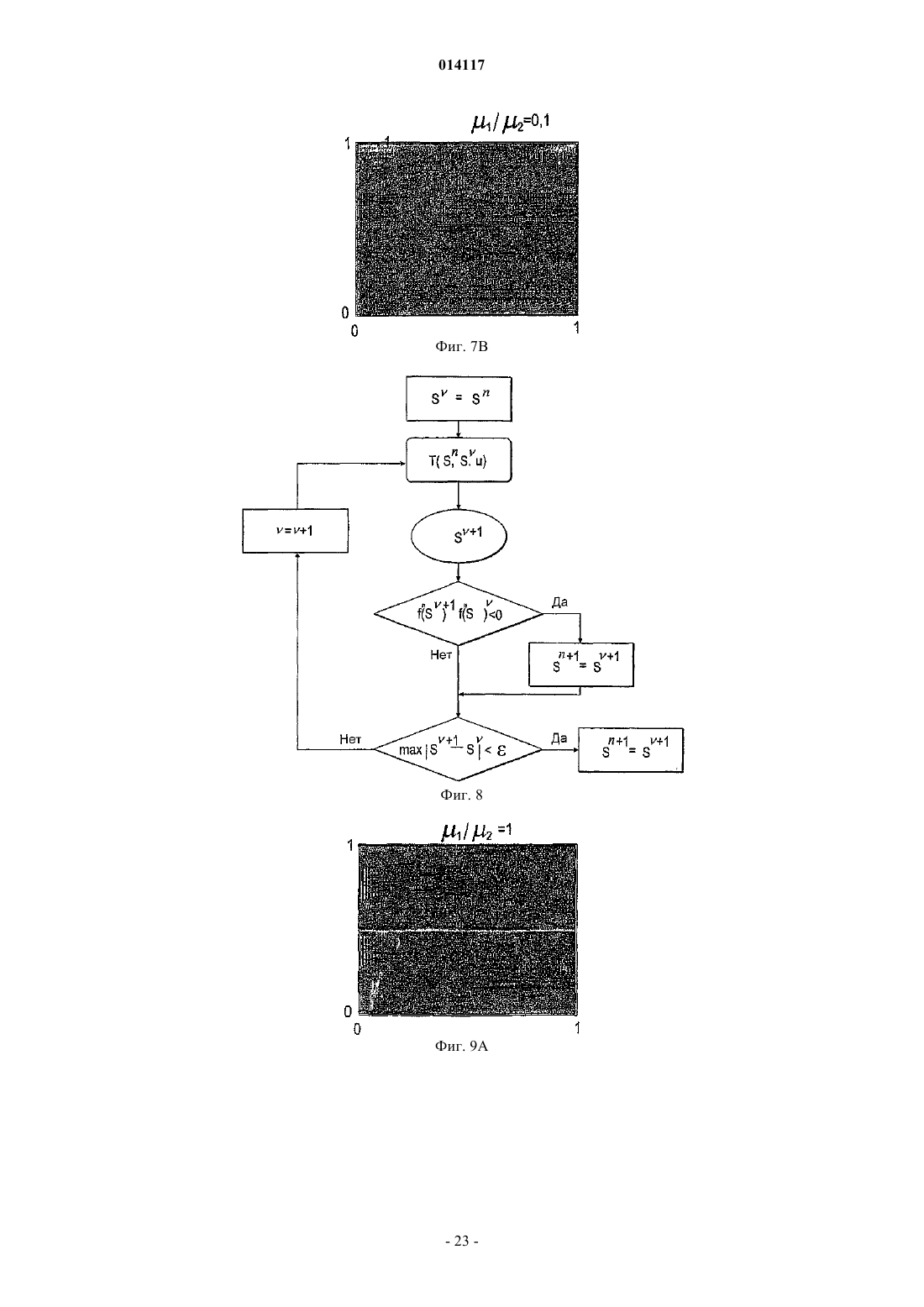
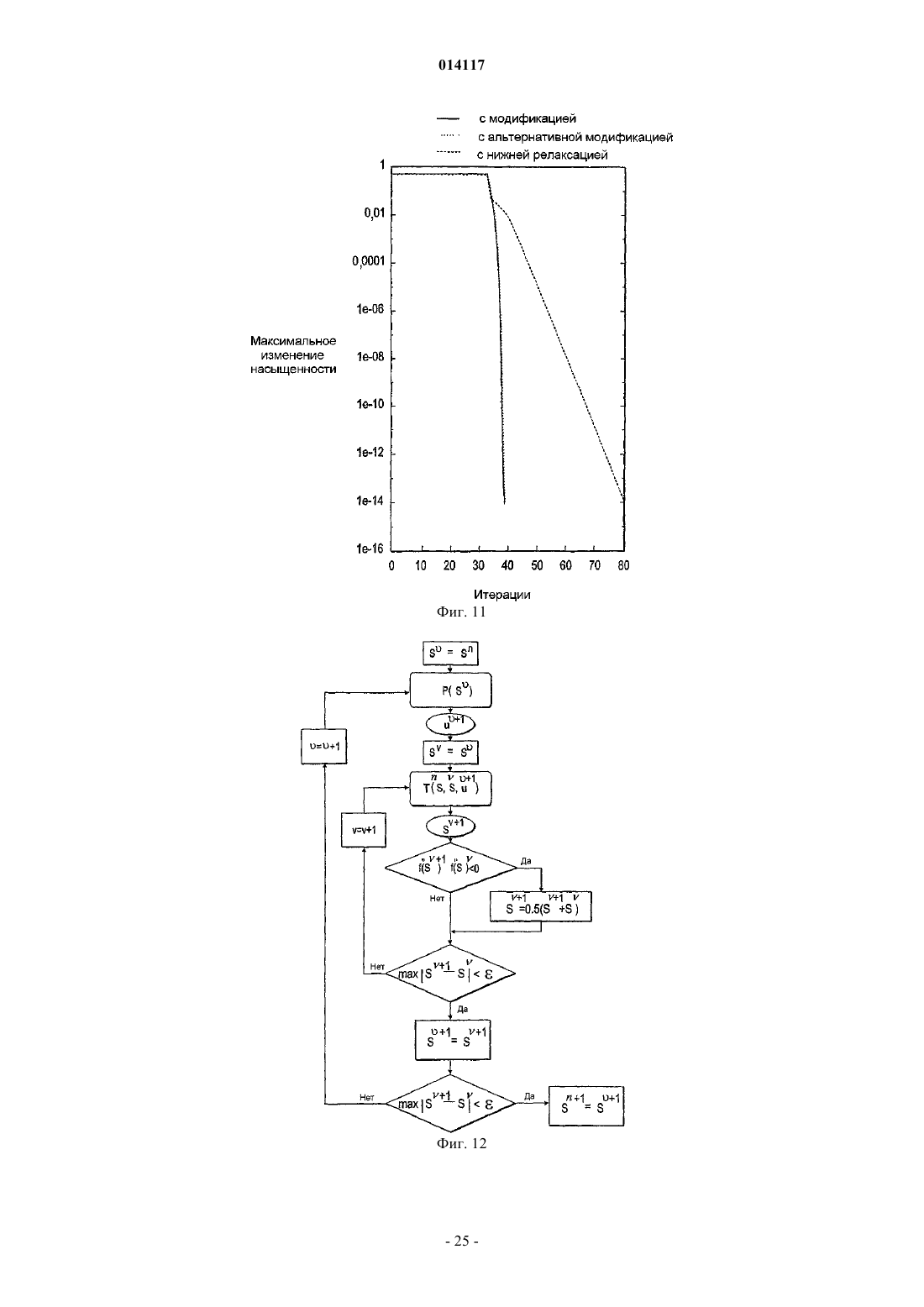
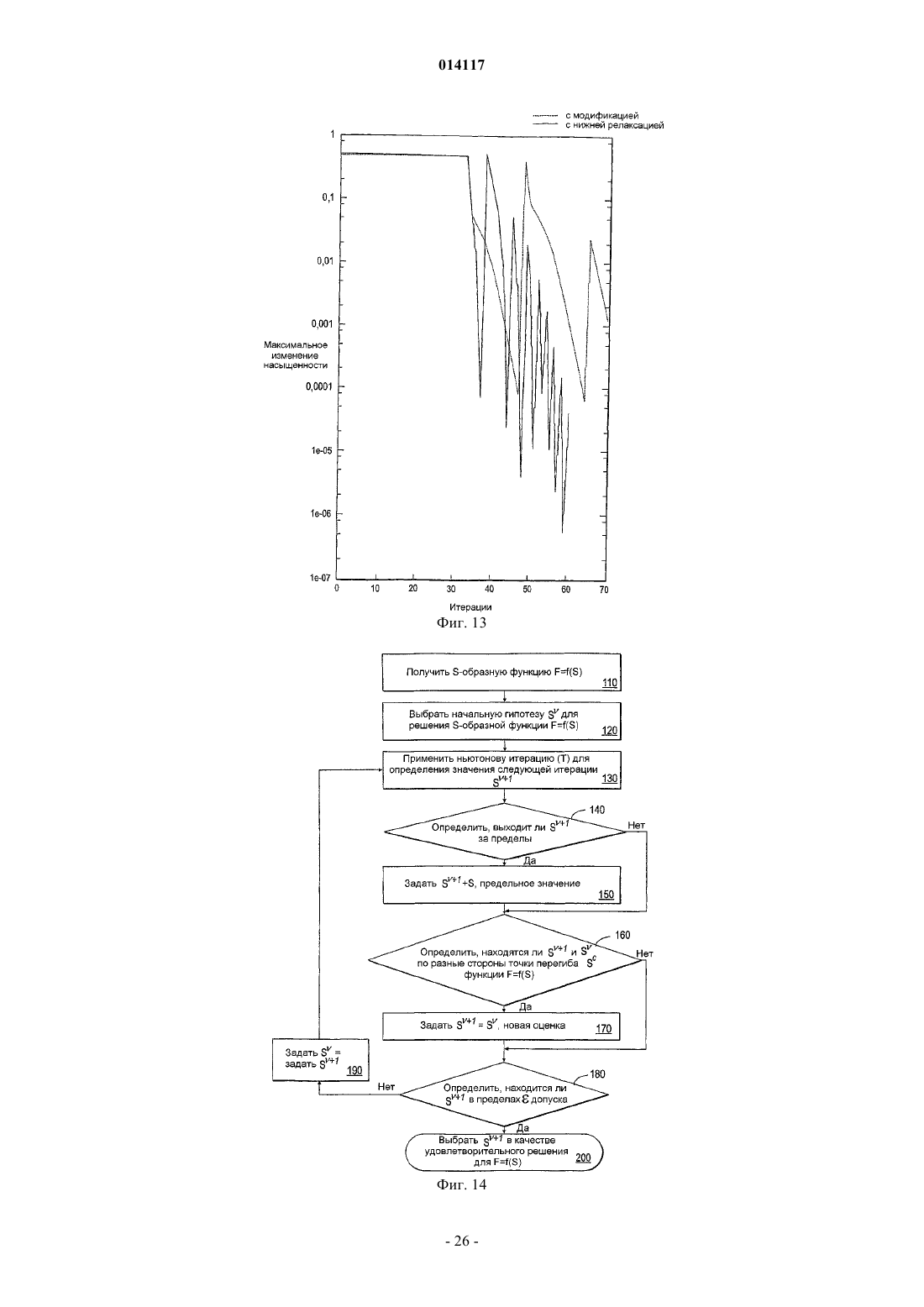
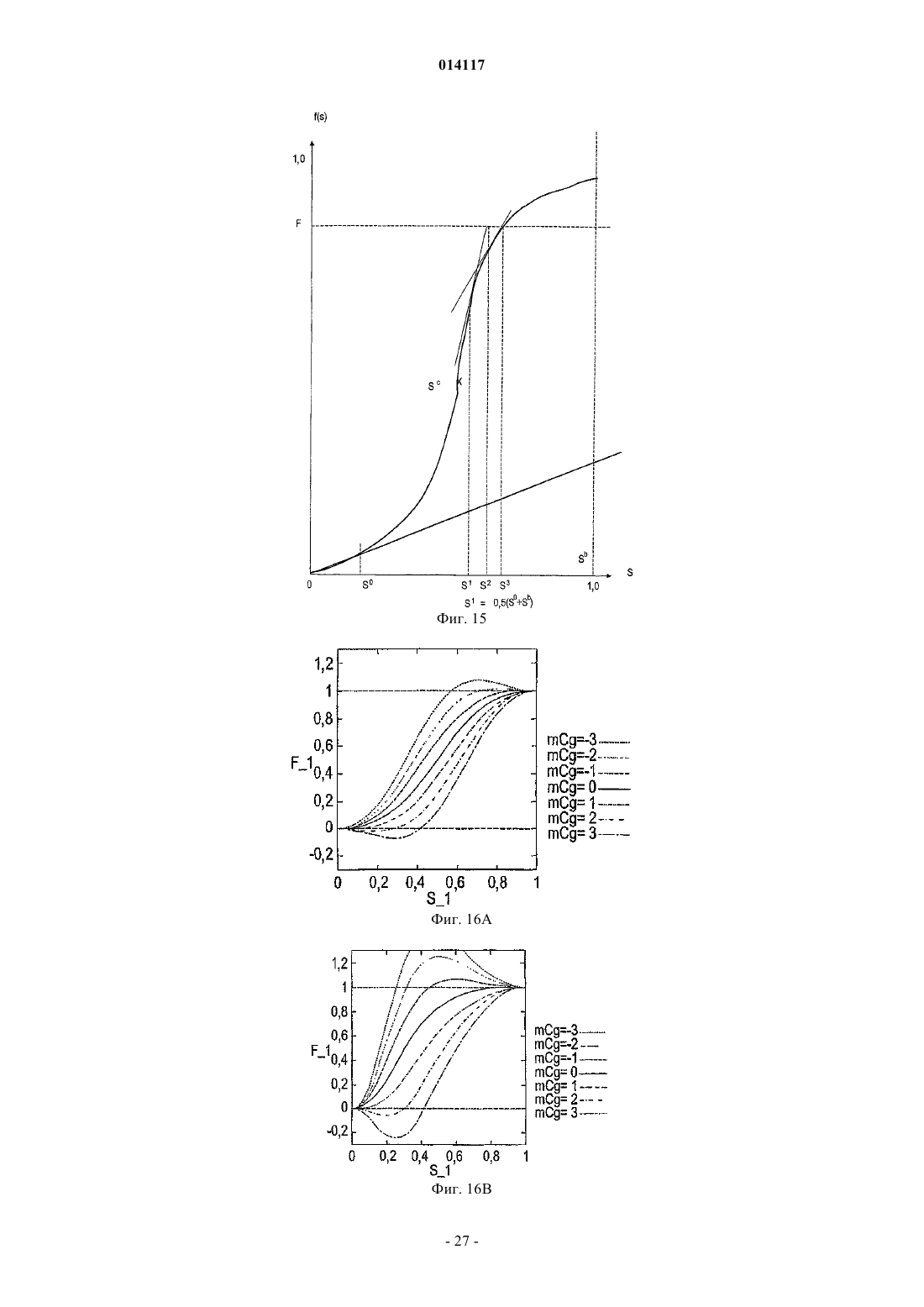
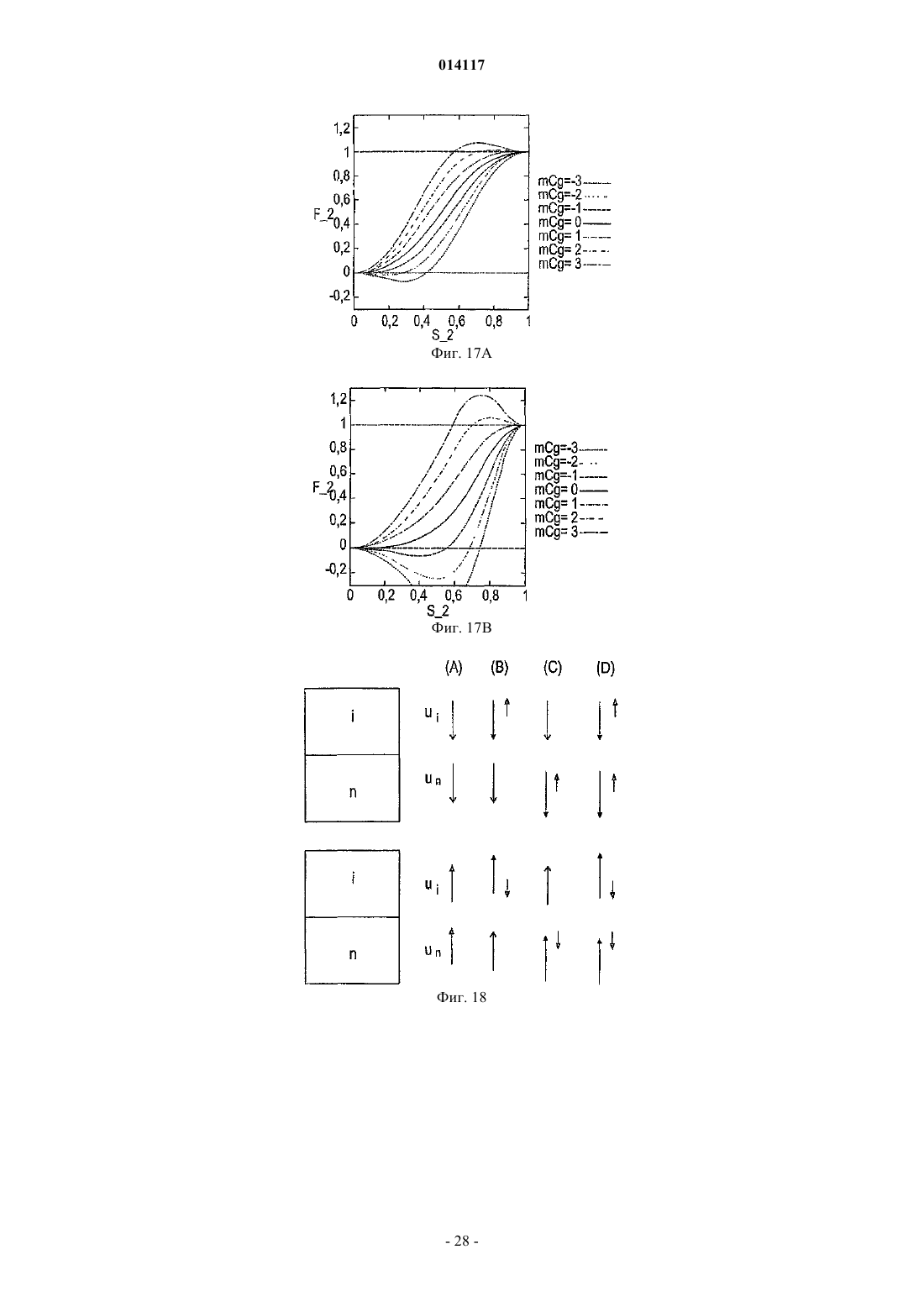
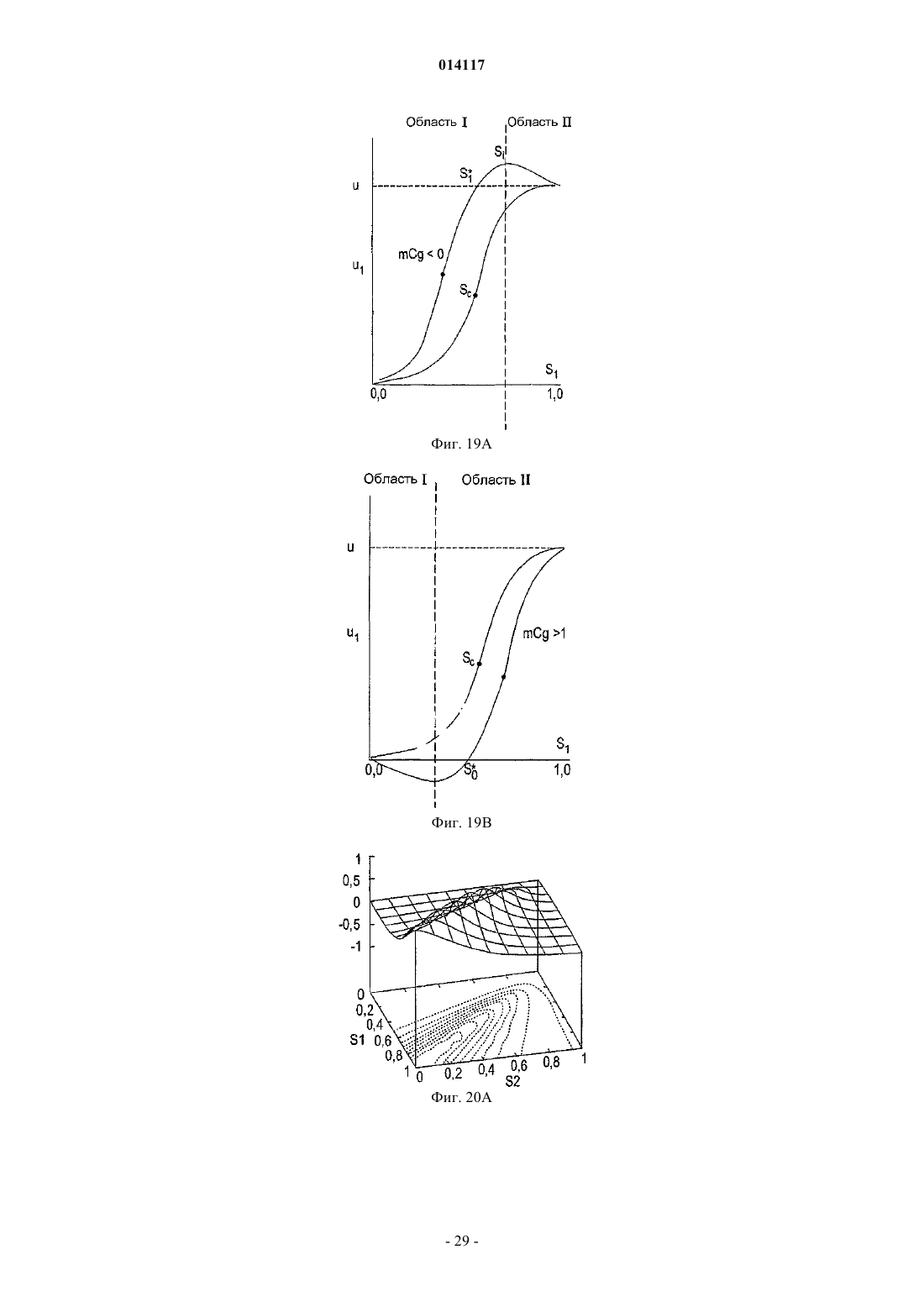
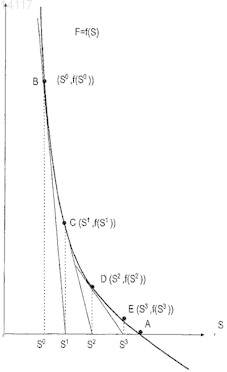
СПОСОБ И УСТРОЙСТВО ДЛЯ МОДЕЛИРОВАНИЯ ИМИТАТОРА КОЛЛЕКТОРА Предусмотрены устройство и способ для моделирования имитатора коллектора посредством решения нелинейной S-образной функции F=(S), которая выражает свойство S в физической системе, например насыщенность, при моделировании коллектора. Итерацию Ньютона (Т) применяют к функции (S) в S для определения значения следующей итерации S+1. Затем определяют, располагается ли S+1 с противоположной стороны точки перегиба Sc относительно S. ЕслиS+1 располагается с противоположной стороны точки перегиба относительно S, то S+1 задают равным S1, что является модифицированной новой оценкой. Модифицированную новую оценкуS1 предпочтительно задавать равной либо точке перегиба Sc, либо среднему значению между S иS+1, т.е. Sl=0,5(S+S+1). Повторяют вышеописанные этапы, пока S+1 не будет удовлетворять заранее определенным критериям сходимости. Кроме того, описаны алгоритмы решения для двухфазного и трехфазного потока с учетом гравитации и капиллярного давления. 014117 Область техники, к которой относится изобретение Настоящее изобретение относится, в целом, к способам и устройствам для маркирования имитатора коллектора с использованием алгоритмов Ньютона-Рафсона и, в частности, к алгоритмам неявного решения для решения нелинейных уравнений, например S-образных функций, связанных с задачами переноса в имитаторах коллектора. Предшествующий уровень техники Алгоритмы неявного решения широко используются для решения нелинейных задач переноса, зависящих от времени, в приложениях вычислительной гидродинамики (CFD), например при моделировании коллектора. Эти алгоритмы неявного решения обычно используются для преодоления ограничений по величине временного шага, присущих методам явного решения. Нередко решение этих задач переноса для нового временного уровня получают с использованием общеизвестного метода Ньютона-Рафсона. На фиг. 1 схематически показано простое выполнение метода Ньютона-Рафсона для решения или,по меньшей мере, приближенного решения для функции F=(S). На фиг. 1 изображен график функции Решение (S)=F=0 определяет корень, т.е. точку, где функция (S) пересекается с горизонтальной осью, т.е. F=0. Эта точка пересечения для S обозначается буквой А. Если эту точку, или удовлетворительно близкую ее аппроксимацию, можно определить, то уравнение (1) считается решаемым. Метод Ньютона-Рафсона требует принятия первоначальной гипотезы для решения. Первоначальная гипотеза обозначается S0 на фиг. 1. Соответствующая точка В на кривой F=(S) имеет координаты(S0, (S. В точке В строится касательная, которая пересекается с горизонтальной осью. Наклон этой касательной равен (S0). Уравнение касательной в общей точке S0 можно алгебраически выразить следующим образом: Решение S является горизонтальной координатой касательной при F=0. Решая уравнение относительно этой координаты, получаем Затем эта координата используется в качестве второй гипотезы или аппроксимации для решения(S)=0 и обозначается S1. Соответственно Наилучшую оценку корня уравнения (1) можно определить, вновь построив касательную в точке с координатами (S1, (S1, т.е. в точке С, и определив точку ее пересечения с горизонтальной осью. При этом получаем Можно видеть, что S2 является более точной аппроксимацией, чем S1 для решения уравнения (1). Еще более точная оценка получается, если построить касательную в точке D, (S2, (S2, что дает пересечение в S3. В общем случае, если начальная аппроксимация или гипотеза для решения F=(S) есть Sn, то следующую аппроксимацию Sn+1 можно получить с использованием Уравнение (6) обеспечивает основную формулу для метода Ньютона-Рафсона. Неоднократно применяя уравнение (6) Ньютона-Рафсона к функции (S), можно определять все более точную аппроксимацию для решения уравнения (1). Однако при этом предполагается, что применение метода НьютонаРафсона для отыскания решения для (S) является безусловно устойчивым. Это не всегда так. При моделировании коллектора функция, подлежащая решению, часто является задачей переноса,линеаризованной вокруг наилучшей оценки решения и решаемой в неявном виде при каждой итерации. В типичном имитаторе коллектора, задача переноса решается для каждой ячейки в модели коллектора при каждой итерации Ньютона-Рафсона. После получения сходящегося решения после некоторого количества итераций Ньютона-Рафсона для временного шага, моделирование переходит к следующему временному шагу. Этот подход является прямолинейным и безусловно устойчивым, если функция плотности потока является выпуклой (ударом), как показано на фиг. 1, вогнутой (волной разрежения) или линейной (слабым разрывом), что справедливо для большинства задач вычислительной гидродинамики(CFD). Однако для S-образных функций плотности потока, которые часто встречаются при моделировании нефтяных коллекторов, метод Ньютона-Рафсона не сходится при выборе слишком больших временных шагов. При моделировании коллектора эту проблему обычно преодолевают, применяя эмпирические методы регулировки временного шага. Однако нередко полученная величина временного шага является консервативной или слишком большой, что приводит к избыточным вычислениям или к обрывам временных шагов. Соответственно, необходим алгоритм неявного решения для решения задач переноса с Sобразными функциями плотности потока, который является безусловно устойчивым независимо от величины временного шага. Настоящее изобретение обеспечивает необходимое решение.-1 014117 Сущность изобретения Предусмотрен способ моделирования имитатора коллектора посредством решения нелинейной Sобразной функции F=(S), которая выражает свойство S в физической системе. S-образная функция имеет точку перегиба Sc и заранее определенное значение F, к которому сходится (S). Первоначальную гипотезу S выбирают как возможное решение функции (S). Итерацию Ньютона (Т) применяют к функции(S) в S для определения значения следующей итерации S+1. Затем определяют, располагается ли S с противоположной стороны точки перегиба Sc относительно S. Если S+1 располагается с противоположной стороны точки перегиба относительно S, то S+1 задают равным Sl, что является модифицированной новой оценкой. Затем определяют, удовлетворяет ли S+1 заранее определенным критериям сходимости. Если нет, то S задают равным S+1 и повторяют вышеописанные этапы, пока S+1 не будет удовлетворять заранее определенным критериям сходимости. Это сходящееся значение S+1 затем выбирают в качестве удовлетворительного решения S для S-образной функции F=(S). Модифицированную новую оценку, Sl,предпочтительно задавать равной либо точке перегиба Sc, либо среднему значению между S и S+1, т.е.Sl=0,5(S+S+1). Альтернативно, можно использовать коэффициент нижней релаксации, отличный от 0,5,например значение, выбранное от 0,3 до 0,7. Кроме того, описаны алгоритмы решения для двухфазного и трехфазного потока с учетом гравитации и капиллярного давления. Задачей настоящего изобретения является способ и устройство для моделирования имитатора коллектора, использующих безусловно устойчивую модифицированную схему Ньютона-Рафсона для решения S-образных нелинейных функций для отыскания приближенных решений задач, поставленных для физических систем. Краткое описание чертежей Эти и другие задачи, признаки и преимущества настоящего изобретения явствуют из нижеследующего описания, формулы изобретения, поданной на рассмотрение, и прилагаемых чертежей, где фиг. 1 - графическое представление итерационного решения функции F=(S) с использованием традиционного метода Ньютона-Рафсона; фиг. 2 - логическая блок-схема для одного временного шага в традиционном имитаторе коллектора,в котором оператор Т представляет решение линеаризованного уравнения переноса, с использованием итерационного метода Ньютона; фиг. 3 - поле проницаемости k в виде сетки 3030 для случая двухмерного теста, которая включает в себя местоположения нагнетательных и продуктивных скважин; фиг. 4 А, 4 В и 4 С - распределения насыщенности поля проницаемости k, показанного на фиг. 3, после нескольких начальных временных шагов; фиг. 5 А и 5 В - карты сходимости выпуклой и вогнутой функций (S) соответственно; фиг. 6 А и 6 В - S-образные функции плотности потока, и фиг. 6 С и 6D - соответствующие карты сходимости, полученные с использованием традиционной схемы Ньютона-Рафсона; фиг. 7 А и 7 В - карты сходимости, полученные с использованием первой модифицированной схемы Ньютона-Рафсона, выполненной в соответствии с настоящим изобретением, для решения S-образных функций, показанных на фиг. 6 А и 6 В; фиг. 8 - логическая блок-схема второй модифицированной схемы Ньютона-Рафсона для одного временного шага, в которой решение линеаризованного уравнения переноса представлено оператором Т; фиг. 9 А и 9 В - карта сходимости согласно второму варианту осуществления модифицированной схемы Ньютона-Рафсона для решения S-образных функций, показанных на фиг. 6 А и 6 В; фиг. 10 А, 10 В, 10 С, 10D, 10 Е, 10F, 10G, 10 Н и 10I соответственно - поля насыщенности спустя время 0,5 объема закачки в поровых объемах (PVI) для трех отношений вязкостей 1/2 и трех величин временного шага; фиг. 11 - истории схождения спустя время 0,5 PVI и 1/2=1 с использованием первой и второй модифицированных схем Ньютона и с использованием схемы Ньютона с постоянной нижней релаксацией; фиг. 12 - логическая блок-схема с непостоянным полем скоростей для одного временного шага, в которой решение уравнения давления представлено оператором Р, и решение линеаризованного уравнения переноса представлено оператором Т; фиг. 13 - истории схождения одного временного шага для трех моделей, две из которых построены согласно модифицированным схемам Ньютона-Рафсона, а третья - с использованием постоянной нижней релаксации на всех итерационных этапах; фиг. 14 - логическая блок-схема этапов, проведенных согласно предпочтительному варианту осуществления настоящего изобретения для решения S-образной функции, F=(S), относительно физического свойства S, например насыщенности; фиг. 15 - графическая иллюстрация итерационного решения S-образной функции F=(S) с использованием модифицированной схемы Ныотона-Рафсона согласно настоящему изобретению; фиг. 16 А и В - кривые фракционного потока для фазы 1 (А) m=1 и (В) m=0,2;-2 014117 фиг. 17 А и В - кривые фракционного потока для фазы 2 (А) m=1 и (В) m=0,2; фиг. 18 А и В - фракционный поток между ячейками i и n: на верхней фигуре, ячейка i ориентирована против потока, и на нижней фигуре ячейка n ориентирована против потока, (А) без противотока; (В) противоток в ячейке I; (С) противоток в ячейке n; и (D) противоток в обеих ячейках i и n; фиг. 19 А и В - кривые фракционного потока для нефтяной фазы (более легкого флюида) с противонаправленными и сонаправленными течениями; фиг. 20 А и В - поверхности фракционного потока без учета гравитационного эффекта для (А) фазы 1 и (В) фазы 2: m1=0,2, m3=10, Cg1=Cg2=0; фиг. 21 А и В - поверхности фракционного потока с учетом гравитационного эффекта для (А) фазы 1 и (В) фазы 2: m1=0,2, m3=10, Cg1=5, Cg2=10; фиг. 22 А и В - поверхности фракционного потока без учета гравитационного эффекта для (А) фазы 1 и (В) фазы 2: m1=0,2, m3=10, Cg1=0, Cg2=0; фиг. 23 А и В - поверхности фракционного потока с малыми гравитационными эффектами для (А) фазы 1 и (В) фазы 2: m1=0,2, m3=10, Cg1=0,5 и Cg2=1,0; фиг. 24 А и В - поверхности фракционного потока с большими гравитационными эффектами для (А) фазы 1 и (В) фазы 2: m1=0,2, m3=10, Cg1=5 и Cg2=10. Подробное описание изобретенияI. Теоретические основы и численные исследования для моделирования коллектора. Рассмотрим следующее гиперболическое уравнение: Уравнение (7) является модельным уравнением, которое описывает перенос одной фазы в задаче двухфазного подземного потока. Зависимой переменной S является насыщенность этой фазы (0S1),является функцией S при 01, и u это поле суммарной скорости с нулевой дивергенцией. Для простоты, но без потери общности, и полагаем постоянным, и полагаем /S0. Нелинейную задачу переноса, выражаемую уравнением (7), можно решить методом итераций, используя традиционный метод Ньютона-Рафсона, обрисованный в логической блок-схеме на фиг. 2. Эта процедура приводит к решению Sn+1 на новом временном уровне. Выдвигается первоначальная гипотезаS для решения S-образной функции. Эта гипотеза может представлять собой значение насыщенности Sn из предыдущего временного шага. В каждой итерациилинеаризованное уравнение переноса предпочтительно решать для каждой ячейки в модели или подмодели коллектора (представленной оператором Т), что позволяет получить обновленное поле насыщенности S+1. После того как максимальное изменение насыщенности от итерации к итерации перестает превышать по абсолютной величине надлежащим образом заданный порог , этот нелинейный цикл считается сходящимся, и S+1 представляет собой решение Sn+1 на новом временном уровне. Рассмотрим двухмерную дискретизацию уравнения (7) которая базируется на неявном эйлеровом и первого порядка продвижении против потока. Для простоты уравнение (8) записано для случая, когда обе составляющие вектора скорости u=ux uyт больше или равны нулю и ортогональны, сетка предполагается однородной. Каждую ячейку сетки можно идентифицировать парой индексов i, j, и шаг сетки по двум осям координат можно обозначить как х и у. Верхние индексы n иобозначают старые временной и итерационный уровни, соответственно, и t это величина временного шага. Для решения уравнения (8) плотность потока n+1 в уравнении (8) линейно аппроксимируется Наконец, аппроксимация S+1 для Sn+1 получается решением линеаризованной системы которая получается подстановкой уравнения (9) в уравнение (8). Важно потребовать, чтобы условие 0S+11 выполнялось всякий раз при решении уравнения (10). Для численных исследований, представленных в этом описании изобретения, для моделирования используется сетка 3030 ячеек. На фиг. 3 показано поле проницаемости k и местоположения нагнета-3 014117 тельной и продуктивной скважин, используемых для вычисления суммарной скорости u=-p путем решения эллиптического уравнения для давления р. Здесьэто - суммарная подвижность где krj - относительная проницаемость фазы j, и j - вязкость фазы. Член источника q равен 1 на продуктивной скважине и (-1) - на нагнетательной скважине и S=0 является начальным условием для насыщенности. В случае простой квадратичной функции иллюстративную S-образную функцию фракционного потока можно представить в виде где 1 и 2 - вязкости двух фаз (нагнетаемая фаза обозначена нижним индексом 1). Для демонстрации того, что описанный выше со ссылкой на фиг. 2 алгоритм неявного решения является неустойчивым при слишком больших временных шагах, приведены результаты для трех численных экспериментов, в которых 1/2 выбрано равным 1, 10 и 0,1 соответственно. На фиг. 4 показаны распределения насыщенности после нескольких начальных временных шагов. Хотя временные шаги сравнительно малы в единицах объема закачки в поровых объемах (PVI), результаты демонстрируют сильное колебательное поведение фронта насыщенности, характеризуемое шаблоном наподобие шахматной доски. Нелинейный цикл алгоритма решения, показанный на фиг. 2, не сходится, и количество итераций ограничивается 200. Перейдем к изучению причины этой неустойчивости или колебательного поведения и опишем модификацию, приводящую к безусловно устойчивой схеме для использования метода Ньютона-Рафсона. Ключом к пониманию вопросов устойчивости нелинейных задач переноса является линеаризация уравнения (9) функции плотности потока. Прежде всего, изолируем нелинейность задачи переноса (S). Затем определяем те начальные значения в диапазоне 0S01, для которых итерационная схема удовлетворяет условиям сходимости(S) вокруг S. Применяя итерационный метод Ньютона, получаем следующее уравнение: Кроме того, после каждой итерации налагаем ограничение 0S1. Теперь исследуем комбинации S0 и F, удовлетворяющие условию (13). Условие (13) всегда выполняется, если функцияявляется линейной, выпуклой или вогнутой функцией S. Поскольку линейный случай тривиален, мы рассмотрим только примеры для выпуклого и вогнутого случаев, которые, соответственно, представлены как (S)=S2 и(S)=1-(1-S)2. На фиг. 5 А и 5 В показаны карты сходимости этих выпуклой и вогнутой функций. Карты сходимости создают, выбирая начальное значение S0 и конечное значение F для функции плотности потока . Затем определяют количество итераций, необходимое для сходимости с заранее определенным допуском к конечному значению F. По горизонтальной оси отложено начальное значение S0, и по вертикальной оси отложено конечное значение F. Этот процесс повторяется для большого количества начальных значений 0S01 при конечном значении F. Затем процесс повторяется для некоторого количества конечных значений 0F1. Это определение количества итераций, необходимого для обеспечения сходимости для каждого значения (S, F), затем отображают графически для создания карты сходимости. Быстрая сходимость обозначена более темной штриховкой, а белый цвет указывает области в параметрическом пространстве, где итерация, выражаемая уравнением (15), не сходится. На фиг. 5A и 5 В нет белых областей,и поэтому итерационная схема является безусловно устойчивой для выпуклой и вогнутой функций (S). Однако ситуация изменяется, если функция плотности потокаявляется S-образной функцией. Sобразная функция отличается наличием выпуклого участка и вогнутого участка, соединяющихся в точке перегиба Sc, как показано на фиг. 6A и 6 В. Точка перегиба Sc это точка, при прохождении через которую вторые производные функции (S), (S) меняют знак. Верхние графики на фиг. 6 А и 6 В отвечают уравнению (12) для 1/2=l и 1/2=0,1 соответственно. Соответствующие карты сходимости показаны на фиг. 6 С и 6D. Наличие больших белых участков отчет-4 014117 ливо показывает, что итерационная схема, применяемая к функции плотности потока , выражаемой уравнением (12), не является безусловно устойчивой для этих значений 1/2. Сходимости можно добиться, если первоначальная гипотеза для S0 близка к окончательному решению, т.е. если (S0)-F не слишком велик. Это согласуется с ограничением величины временного шага или максимального изменения насыщенности при решении задачи переноса. Карты сходимости, показанные на фиг. 6 С и 6D, демонстрируют, что итерационное уравнение (15) сходится для всех возможных конечных значений F, если S0=Sc, где Sc - точка перегиба . Это определение подразумевает задание S+1=Sc, если вторые производные функций (S) и (S+1) имеют противоположные знаки. Если это делать в конце каждой ньютоновой итерации, получится модифицированная схема Ньютона-Рафсона, которая является безусловно устойчивой для S-образных функций плотности потока. На фиг. 7 А и 7 В показаны карты сходимости для S-образных функций плотности потока, представленных на фиг. 6 А и 6 В. Однако на этот раз применяется первая модифицированная схема НьютонаРафсона, предусматривающая задание S+1=Sc, если вторые производные функций (S) и (S+1) имеют противоположные знаки. Это можно проверить следующим вычислением: Если произведение вторых производных отрицательно, значит S и S+1 находятся по разные стороны точки перегиба S0. По горизонтальной оси отложено начальное значение S0, и по вертикальной оси отложено конечное значение F. Темные области указывают быструю сходимость, а для пар параметров на белых участках невозможно добиться сходимости. Заметим, что на фиг. 7 А и 7 В нет белых участков, и, таким образом,эта первая модифицированная схема Ньютона-Рафсона является безусловно устойчивой. Применение этой модификации к алгоритму решения задачи переноса является прямолинейным и допускает сколь угодно большие временные шаги. Определение точного местоположения точки перегиба Sc может оказаться трудной задачей. Это особенно верно при решении системы уравнений переноса, где функции фракционного потока зависят от нескольких переменных. В ряде случаев для представления кривой фракционного потока (S) можно использовать поисковые таблицы, и точки перегиба нелегко вычислить аналитически. Кроме того, отыскание точки перегиба Sc сложных функций фракционного потока может требовать больших объемов вычислений. Поэтому представлена альтернативная и более предпочтительная вторая модифицированная схема,которую проще реализовать в реальной ситуации. Эта вторая схема отличается от первой схемы тем, чтоS+1 модифицируется в конце каждой ньютоновой итерации, где S и S+1 располагаются по разные стороны точки перегиба Sc кривой . Вместо задания S+1 равным Sc, применяется метод избирательной нижней релаксации. Например, S+1 можно заменить 0,5(S+S+1), если знак второй производной, т.е.(S)=2/S2, неодинаков на старом и новом уровнях итерации. Также можно использовать другие уровни релаксации. Таким образом, нижнюю релаксацию можно обобщить следующим образом: где Sl = новая оценка для S; и= коэффициент нижней релаксации. Логическая блок-схема этой второй усовершенствованной схемы представлена на фиг. 8. Поскольку относительно легко определить вторые производные , эту вторую альтернативную схему легко реализовать в существующем имитаторе нефтяного коллектора по сравнению с первой модифицированной схемой, где S+1 задается равным Sc, когда S и S+1 находятся по разные стороны Sc. По аналогии с картами сходимости, показанными на фиг. 6 С и 6D и фиг. 7 А и 7 В, соответствующие карты сходимости для второй альтернативной модификации, использующей избирательную нижнюю релаксацию, показаны на фиг. 9 А и 9 В. По горизонтальной оси отложено начальное значение S0 и по вертикальной оси отложено конечное значение F. Темные области указывают быструю сходимость, а для пар параметров на белых участках невозможно добиться сходимости. Что касается карт сходимости, показанных на фиг. 7 А и 7 В, там нет белых участков, и это говорит о том, что эта вторая альтернативная модификация обеспечивает безусловно устойчивую схему. И первая, и вторая модификация действует предсказуемым образом, если они применяются к алгоритму решения нелинейных уравнений переноса. Первая и вторая модифицированные схемы почти одинаково эффективны. Кроме того, если величина временного шага находится в пределах диапазона устойчивости для немодифицированной или традиционной схемы Ньютона-Рафсона, модификации этого изобретения не приведут ни к какому снижению эффективности численных исследований. С другой стороны, эффективность сильно снижается, если устойчивость достигается за счет применения нижней релаксации в конце каждой ньютоновой итерации повсеместно, а не избирательно, как в вышеописанных модифицированных схемах. На фиг. 10 А-I представлены численные результаты для вышеописанного случая теста с использованием S-образных функций фракционного потока, заданных уравнением (12). Все модели были построены с помощью первой и второй модифицированных схем и показано, что можно-5 014117 применять сколь угодно большие временные шаги. На фиг. 10 А-I, соответственно, показаны поля насыщенности, полученные спустя время = 0,5 PVI при 1/2=1 (верхняя строка - фиг. 10 А, 10 В и 10 С),1/2=10 (средняя строка - фиг. 10D, 10 Е и 10F) и 1/2=0,1 (нижняя строка - фиг. 10G, 10 Н и 10I). Результаты, приведенные в левом столбце этих графиков, были вычислены с использованием 100 малых временных шагов или t=0,005 PVI, что также обеспечивает устойчивость немодифицированной схемы Ньютона-Рафсона. Заметим, что эти временные шаги в два раза меньше тех, которые используются для получения несходящихся результатов, представленных на фиг. 4, средний и правый столбцы графиков демонстрируют результаты, вычисленные при t=0,1 PVI и t=0,5 PVI соответственно. На фиг. 11 показаны результаты использования вышеописанных первой и второй модифицированных схем Ньютона-Рафсона, в которых S+1 избирательно задается Sc и 0,5(S+S+1) соответственно, только когда знаки вторых производных '(S) и '(S+1) меняются на этапе итерации. Кроме того, была исследована третья схема, в которой нижняя релаксация применяется в конце каждой итерации, т.е. наивная схема нижней релаксации. По вертикальной оси отложено максимальное изменение насыщенности на этапе итерации и по горизонтальной оси отложено количество итераций. На фиг. 11 представлен график для случая, когда величина временного шага равна 0,5 PVI, и отношение вязкостей 1/2 равно единице. Для всех построенных моделей первую и вторую модифицированные схемы тестировали, и при этом не наблюдалось никаких заметных отличий в отношении необходимого количества итераций. В то время как темп сходимости первых двух схем, по существу, одинаков, показано, что третья схема с наивной нижней релаксацией значительно менее эффективна. Модифицированные схемы Ньютона-Рафсона также применимы в качестве строительного блока для алгоритма решения, если коэффициент подвижности X является функцией насыщенности. Они представляют особый интерес для нефтедобывающей промышленности. В случае квадратичной относительной проницаемости, коэффициент подвижности X выражается в видеS - насыщенность первой фазы; 1 - вязкость первой фазы и 2 - вязкость второй фазы. Вследствие того, чтоявляется функцией насыщенности, поле скоростей u уже не является постоянным и подлежит обновлению путем решения уравнения давления (18), еслиизменяется. Этот алгоритм представлен логической блок-схемой на фиг. 12. Заметим, что логическая блок-схема на фиг. 8 снова появляется в заштрихованном прямоугольнике в цикле, необходимом для обновления поля суммарных скоростей u. Это сходящееся решение идентично решению, полученному посредством полностью неявной схемы, где уравнения давления и переноса решаются одновременно. На фиг. 13 показаны истории схождения одного временного шага для двух построенных моделей,одна из которых была построена с помощью модифицированного алгоритма решения Ньютона-Рафсона с использованием избирательной нижней релаксации, а другая - методом, предусматривающим использование простой или наивной нижней релаксации. Случай теста был таким же, как в предыдущих исследованиях, величина временного шага была равна 0,5 PVI, и отношение вязкостей 1/2=1. С помощью модифицированного алгоритма, линеаризованное уравнение переноса пришлось решать приблизительно 60 раз, а эллиптическое уравнение давления - только девять раз (количество пиков на графике сходимости). С другой стороны, простая или наивная нижняя релаксация оказалась гораздо менее эффективной. Иллюстративные этапы для решения S-образной функции относительно физического свойства. Настоящее изобретение включает в себя способ и устройство для устойчивого решения нелинейныхS-образных функций F=(S) для определения свойства S, представляющего физическую систему. На фиг. 14 показана предпочтительная иллюстративная логическая блок-схема этапов, которые можно использовать для осуществления изобретения согласно принципам, описанным в предыдущем разделе. На фиг. 15 графически представлена модифицированная схема Ньютона. В этом модифицированном алгоритме Ньютона-Рафсона, значение для следующей итерации, S+1,задается равным новой оценке или пределу устойчивости Sl в случае, когда знаки вторых производных,(S) и '(S+1), S-образной функции изменяются между последовательными итерациями. Модифицированная новая оценка, или предел устойчивости, Sl, в идеальном случае, выбирается так, чтобы модифицированный метод Ньютона-Рафсона гарантировал устойчивую сходимость. На первом этапе 110 получают S-образную функцию (S), которая выражает свойство S физической системы. Например, особый интерес представляет физическая система потоков флюидов в геологическом пласте. S-образную функцию (S) можно выразить в виде математической функции, например посредством вышеприведенного уравнения (12) или посредством поисковой таблицы для выражения сущности S-образной функции. Как известно специалистам в области моделирования коллектора, S-6 014117 образную функцию, например функцию фракционного потока, можно получить из лабораторных испытаний на основании измерений относительной проницаемости. Специалистам в области решения нелинейных задач для физических систем очевидно, что настоящее изобретение, предусматривающее использование модифицированных схем Ньютона-Рафсона, можно использовать для решения S-образных функций, которые характеризуют свойства физических систем,отличных от моделирования коллектора.S-образная функция (S) отличается наличием, по меньшей мере, выпуклого участка и вогнутого участка, соединенных в точке перегиба Sc. Функция (S) подлежит решению для определения физического свойства S, удовлетворяющего условию F=(S), где F - конечное значение. Например, при моделировании коллектора при решении S-образной функции фракционного потока (S) относительно значения насыщенности S в ячейке сетки в линеаризованной задаче переноса значение плотности потока F из предыдущего временного уровня идеально используется в качестве конечного значения F. Альтернативно,конечное значение F можно установить путем нелинейной итерации в численном моделировании. Начальное(ая) значение или гипотеза S выбирается на этапе 120 в качестве возможного решения для физического свойства S, удовлетворяющего условию F=(S). Это начальное значение для S предпочтительно определяется начальным условием или результатами предыдущего временного шага. Хотя это и менее предпочтительно, начальное значение для S+1 также можно получить методом интерполяции или рандомизированным методом. Итерационный метод Ньютона, представленный оператором (Т) на фиг. 8, осуществляется на этапе 130 для функции (S) с использованием значения S текущей итерации для определения значения следующей итерации S+1. Этот итерационный метод Ньютона соответствует применению уравнения (15) кS-образной функции (S) для определения значения следующей итерации S+1. Согласно фиг. 15, эта первоначальная гипотеза равна S0. На этапе 140 можно проводить необязательную проверку, находится ли S+1 в приемлемых пределах. Например, если знаменатель в S-образной функции, например функции, аналогичной, представленной уравнением (12), близок к нулю, оценочное значение для S+1 будет весьма велико. Если S+1 превышает определенные предельные значения, например насыщенность S меньше нуля или больше единицы,то S+1 можно занять на этапе 150 равным значениям, например, 0,0 или 1,0 для поддержания физического свойства S, в реалистических пределах. В примере, показанном на фиг. 15, видно, что пересечение касательной к точке (S0, (S0 с горизонтальной линией, представляющей значение плотности потока F,происходит вне верхнего предела насыщенности, S=1,0. Соответственно, S+1 в случае первой итерации на фиг. 15 задают равным верхней границе Sb=1,0. Затем, на этапе 160, определяют, находятся ли S и S+1 по разные стороны точки перегиба Sc Sобразной функции (S). Такое определение предпочтительно производить так, чтобы проверить, что знаки второй производной (S), т.е. '(S), в S и в S+1 противоположны друг другу. Это можно проверить с использованием уравнения (16) для вычисления произведения (S) и "(S+1). Если произведение вторых производных отрицательно, то S и S+1 находятся по разные стороны точки перегиба. Другой, хотя и менее предпочтительный подход к производству этого определения состоит в фактическом вычислении положения точки перегиба Sc с последующим определением, лежат лиS и S+1 по одну сторону от Sc. Точку перегиба Sc можно вычислить, решая уравнение '(S)=0. Это можно сделать аналитически, если функция (S) достаточно проста, или же численным методом, если (S) сложна. В случае использования поисковой таблицы для задания S-образной функции (S), можно генерировать начальную таблицу значений для (S), '(S) и (S). Затем поисковые таблицы можно исследовать для определения местоположения точки перегиба Sc. Согласно фиг. 15, значения S0 и Sb располагаются по разные стороны точки перегиба Sc. Если S и S+1 находятся по разные стороны точки перегиба Sc, то, чтобы гарантировать безусловную устойчивость при решении относительно S, на этапе 170 S+1 задают равным Sl, новой оценке или пределу устойчивости. Эту модифицированную оценку S выбирают, чтобы гарантировать сходимость итераций Ньютона-Рафсона. В первом предпочтительном варианте осуществления модифицированную оценку Sl выбирают равной точке перегиба Sc. Согласно второму, более предпочтительному подходу,показанному на фиг. 15, для вычисления Sl используется метод нижней релаксации. В идеальном случае,Sl вычисляется согласно следующему уравнению: где 01. Предпочтительно диапазонпредставляет собой 0,30,7, еще более предпочтительно 0,40,6 и наиболее предпочтительно =0,5. При =0,5, S+1 или Sl задается равным 0,5(S+S+1). Если определено, что S и S+1 расположены по одну сторону точки перегиба Sc, то S+1 предпочтительно остается неизменным вместо того, чтобы быть заданным равным модифицированной оценке Sl,т.е. Sc или Sl=0,5(S+S+1).-7 014117 На этапе 180 производится определение, отвечает ли текущее итерационное значение S+1 заранее определенному условию допуска. Например, может потребоваться, чтобы разность между последовательными итерационными значениями S и S+1 была достаточно мала. Математически это можно выразить как где- заранее определенный предел допуска. Альтернативно, может потребоваться, чтобы чтобы рассматривать решение S+1 как достаточно близкое к точному решению. Если S+1 не считается удовлетворительным решением, то S задается равным S+1 на этапе 190, и этапы 130-180 продолжаются, пока значение S+1 не сойдется в заранее определенном пределе допуска. На фиг. 15 показано, как последовательные оценки насыщенности S1, S2 и S3 и т.д. сходятся к точному решению для насыщенности S. По достижении достаточной сходимости физическое значение S считается удовлетворительным решением. В случае имитатора коллектора насыщенность S в ячейках сетки для следующего временного уровня Sn+1 можно задать равным S+1 по достижении схождения для каждой из ячеек сетки, к которым применяется модифицированный итерационный метод Ньютона. Настоящее изобретение дополнительно включает в себя устройство или устройство для хранения программ, считываемое машиной, в котором материально реализована программа, состоящая из команд. Эти команды выполняются машиной для осуществления этапов способа для устойчивого решения нелинейной S-образной функции, F=(S), которая выражает свойство S физической системы. S-образная функция имеет точку перегиба Sc и заранее определенное значение F, к которому сходится (S). Способ содержит следующие этапы. Выбирают начальное значение S для возможного решения F=(S). Применяют итерационный метод Ньютона к функции (S) в S для определения значения следующей итерацииS+1. Затем определяют, располагается ли S+1 с противоположной стороны точки перегиба Sc относительно S. Если S и S+1 расположены по разные стороны, то S+1 задают равным Sl, модифицированной новой оценке. Затем проводят проверку, чтобы определить, является ли S+1 удовлетворительным решением для свойства S, определяя, удовлетворяет ли S+1 заранее определенным критериям сходимости. Если S+1 не удовлетворяет критериям сходимости, то S задают равным S+1. Повторяют вышеописанные этапы, пока S+1 не будет удовлетворять заранее определенным критериям сходимости. По достижении сходимости, S+1 выбирают в качестве удовлетворительного решения задачи F=(S).II. Алгоритм для двухфазного потока с учетом гравитации и капиллярного давления. Изучим влияние гравитации и капиллярного давления на численную устойчивость метода НьютонаРафсона для нелинейного уравнения переноса, описывающего двухфазный поток. Эффекты гравитации и/или капиллярного давления при моделировании коллектора могут приводить к противотоку в ячейках коллектора. Такой противоток может привносить значительную численную неустойчивость в традиционные имитаторы коллектора. Распространяя способ, описанный выше в разделе I, можно вывести безусловно устойчивый алгоритм для нелинейного уравнения переноса для двухфазного потока с учетом гравитации и капиллярного давления. Прежде всего, рассмотрим влияние гравитации на кривые фракционного потока. Затем охарактеризуем кривые фракционного потока посредством характеристического параметра. После этого опишем безусловно устойчивый алгоритм для двухфазного потока с учетом гравитации. Также обеспечим модификацию безусловно устойчивого алгоритма для включения эффекта капиллярного давления. Гравитационный эффект Закон Дарси для двухфазного потока с учетом гравитации можно выразить в виде Здесь k - проницаемость, u - фазная скорость, kr - относительная проницаемость,- вязкость, D глубина и p - плотность. Нижние индексы обозначают свойства фазы. Из уравнений (22) и (23) можно легко получить где S обозначает насыщенность фазы 1 (т.е. воды). Суммарная скорость задается как где uc - характеристическая скорость и D глубина. Заметим, что скорости u, u1 и u2 в уравнениях (24) и (25) также являются безразмерными величинами, приведенными к uc. Исследуем кривые фракционного потока на основании уравнений (24) и (25). На фиг. 16 и 17 построены графики фракционных потоков для фаз 1 и 2 соответственно Кривые фракционного потока монотонны, если 0mCg1, тогда как они могут стать многозначными функциями для mCg1 или mCg0. Заметим, что фракционный поток может быть меньше нуля или больше единицы в зависимости от направлений силы тяжести и скорости. Это может привести к численной трудности, если метод нелинейных итераций Ньютона не учитывает фактическую картину этих кривых. Заметим, что кривая фракционного потока с отрицательной Cg и положительной и эквивалентны кривым с положительной Cg и отрицательной u. При практическом моделировании с фиксированными координатами Cg можно поддерживать всегда постоянной, но средняя скорость может быть как положительной, так и отрицательной. Заметим, что, без потери общности, случай отрицательной средней скорости эквивалентен случаю положительной средней скорости при отрицательной Cg за счет выбора надлежащей координаты для того, чтобы средняя скорость была положительна. Если в качестве первичного уравнения из уравнения (25) выбрано уравнение для нефти (более легкого флюида), насыщенность, где фракционный поток нефтяной фазы оказывается равным нулю S0 или единице S1 Если mCg/u1 для u0, фракционная кривая оказывается монотонной кривой; тогда как, если u0 или mCg/u1 для u0, кривая фракционного потока включает в себя область, где фракционная кривая оказывается многозначной (немонотонной). Когда кривая фракционного потока имеет точку минимума или максимума, существует точка отражения, которую насыщенность при нелинейной итерации не пересекает (см. фиг. 19). Эту точку отражения можно вычислить аналитически, если относительные проницаемости являются квадратичными, как в уравнениях (33) и (34). Кубическое уравнение можно решать аналитически и всегда имеет по меньшей мере один действительный корень Насыщенность можно разделить на две области: (1) SSr и SSr. В общем случае, насыщенность не пересекает точку отражения, но если ячейка находится вблизи границы без потока или граничит с ячейкой с насыщенностью другой области, насыщенность должна иметь возможность пересекать ее. Кривая фракционного потока не применяется ввиду наличия границы, которая допускает накопление флюида без противотока. Аппроксимация методом конечных разностей Кривые фракционного потока, изображенные на фиг. 16 и 17, указывают, что двухфазный поток может быть сонаправленным и противонаправленным в зависимости от характеристической переменнойCg и отношения вязкостей, m и насыщенности S. Как видно из фиг. 18, когда фракционный поток в ячейке i и соседней ячейке n не создают противоток, общую аппроксимацию методом конечных разностей против течения можно применять без неопределенности. Однако если противоток имеет место в ячейке i или ячейке n, как показано на фиг. 18, то, что выше по течению. Разделение фаз из суммарной скорости, вычисляемое в решении относительно давления, в результате обеспечивает подробную информацию о сонаправленном или противонаправленном потоке между ячейками i и n. На фиг. 18 представлены все возможные случаи, которые могут иметь место между ячейкой i и соседней с ней ячейкой n. Предполагается, что суммарная скорость из решения относительно давления, u, это скорость на границе раздела ячеек i и n, и суммарные скорости внутри ячеек i и n равны,скажем, u. В ячейке i фазные скорости, которые сонаправлены и противонаправлены, выражаются через суммарную скорость u и обозначаются как upi и uri соответственно. Эти фазные скорости можно получить из уравнения (24) или (25). Уравнения можно выразить в виде Если ячейка i находится выше по течению,и если ячейка n находится выше по течению,Заметим, что предполагается, что конкретная фазная скорость может быть сонаправлена или противонаправлена в зависимости от направлений потока и гравитации. Кроме того, противоток не возникает,если 0mCg1. В последовательном неявном алгоритме уравнения насыщенности решаются методом итераций при фиксированной суммарной скорости для выполнения условия сохранения массы (т.е. нулевой дивергенции). Этот алгоритм можно напрямую реализовать посредством соотношения между суммарной скоростью и фракционным потоком. Однако для случая противотока исходный фракционный поток, который зависит от одной насыщенности, нужно модифицировать для обеспечения сохранения массы. Если фазная скорость ui определена из ячейки i, находящейся выше по течению, то фракционный поток ячейки Тогда суммарную скорость можно выразить в виде Проверка устойчивости Вопросы устойчивости нелинейных задач переноса заключаются в линеаризации функции плотности потока. Заметим, что уравнение насыщенности теперь является функцией насыщенности ячейки и насыщенностей всех ячеек, находящихся выше по течению. Численные схемы были испытаны на предмет того, могут ли схемы сходиться от начальной оценки насыщенности, 0S01, для всех ячеек, к конечной насыщенности S, которая удовлетворяет критерию сходимости где F0 - правосторонний вектор. В уравнении (56) насыщенности выражаются в векторной форме. Линеаризация F(S) вокруг S дает откуда получается уравнение итерации Кроме того, после каждой итерации требуется, чтобы 0Sj+11 для всех j. При построении 3-мерной модели методом конечных разностей гравитационный параметр Cg зависит от направления потока (т.е. Cg=0 для горизонтального потока Fh, и Cg0 для вертикального потокаF). В результате приходится рассматривать две кривые фракционного потока, для горизонтального Fh и вертикального потока F. Вертикальный поток F может оказаться немонотонной кривой для mCg1. Уравнение насыщенности более легким флюидом (S0) решается, и другая фаза вычисляется, исходя из ограничения по насыщенности (Sw=1-S0). Учет гравитации При дополнительном учете гравитации кривая фракционного потока F=(S) может изменяться, см. уравнения (31) и (32), в результате чего эти кривые могут содержать точку отражения Sr. Как описано выше, Cg, см. уравнение (30), вычисляется и используется в уравнениях (24) и (25) при окончательном построении этой кривой фракционного потока F(S). В случае отсутствия противотока, кривые фракционного потока останутся, как описано в разделе I,без точек отражения Sr. Однако при наличии противотока кривые, например, показанные на фиг. 19 А-В,могут содержать точку отражения Sr. Области I и II можно определить как области, разделенные точкой отражения Sr, причем область I является областью под точкой отражения 0SSr, и область II является областью над ней SrS1,0. В случае, когда ячейка сетки, для которой оценивается S, находится около границы без потока, метод, описанный выше в разделе I, применяется независимо от наличия или отсутствия точки отраженияSr. Дело в том, что при этих условиях противоток не может возникать. Альтернативно, если S в соседних ячейках i и n находятся в разных областях I и II, то метод, описанный выше в разделе I, используется для того, чтобы насыщенность S+1 могла переходить через точку отражения Sr. В случае, когда ячейка сетки i (1) не находится на границе без потока, или (2) ячейки i и n находятся в одной и той же области, S+1 определяется для конкретной области, в которой располагается S. Например, если S располагается в области I, то S+l будет поддерживаться в области I. Если '(S)'(S+1)0, то нижняя релаксация не требуется для обеспечения устойчивости. Однако S+l будет задано равным либо 0,либо Sr в случае, когда S+l оказывается вне области I. Если '(S)'(S+l)0, т.е. по разные стороны от точки перегиба Sc в этой области, то нижняя релаксация будет использоваться для обеспечения устойчивости. Опять же, если S+l оказывается вне области I, в которой находится S, S+l будет задано равным нижнему или верхнему предельному значению, 0 или Sr, до вычисления обновленного или нижнерелак- 11014117 сированного значения S+1, т.е. 0,5(S+S+1). Аналогично, в области II осуществляется проверка S и S+1 на предмет того, находятся ли S и S+1 по одну сторону от точки перегиба Sc в области II. Если это так, то для устойчивости не требуется нижняя релаксация - только производится проверка, чтобы удостовериться, что S+1 находится в области II. Если S и S+1 находятся по разные стороны точки перегиба Sc в этой области, т.е. '(S)'(S+1)0, то используется нижняя релаксация, т.е. S+1 = 0,5(S+S+1). Опять же, S+l должно попадать в область II до производства последующего вычисления нижней релаксации. Капиллярное давление легко включить в вышеописанные этапы. задается равным Cg-Ca, что будет описано ниже в уравнении (65). Просто В этот момент S+1 определено для этой итерации +1 для этой конкретной ячейки сетки i. Согласно разделу I проверка сходимости осуществляется на каждой из ячеек сетки модели или подмодели, чтобы установить, достигнута ли сходимость во всех ячейках сетки, чтобы установить, что временной шаг выполнен и что больше не требуется никаких ньютоновых итераций для временного шага. Алгоритм обновления SS+1 в ячейке сетки Следующий алгоритм можно использовать для двухфазного потока с учетом гравитации. 1. Проверить направления фазных скоростей и силы тяжести. 2. Если фазные скорости сонаправлены, применить обычный анализ устойчивости: вычислить направленные фракционные потоки и их производные второго порядка (Fh и F ); вычислить Cg для вертикального потока (для горизонтального потока, Cg=0) и применить предел насыщенности 0S+11; если Fh(S+1)Fh"(S)0 или F"(S+1)F"(S)0, применить нижнюю релаксацию для итерации насыщенности, т.е. S+1 = 0,5 (S+S+1). 3. Если фазные скорости противонаправлены,вычислить точку отражения насыщенности Sr и применить предел насыщенности: если ячейка не соседствует с границей или соседняя ячейка не принадлежит другой области насыщенности, то 0S+1Sr или SrS+11, иначе 0S+11. если Fh(S+1)Fh"(S)0 или Fh(S+1)Fh"(S)0, применить нижнюю релаксацию для итерации насыщенности: т.е. S+1=0,5(S+S+1). Капиллярное давление В многофазном потоке в пористых средах флюидам свойственно находиться под разными давлениями вследствие различия их способности к смачиванию породы и поверхностного натяжения между флюидами. Это капиллярное давление часто моделируют простой функцией насыщенности Предполагается, что фаза 1 является смачивающей, а фаза 2 - несмачивающей. В общем случае капиллярное давление определяет микроскопические потоки в порах, но играет подчиненную роль при моделировании коллектора в целом. Поэтому не предполагается, что капиллярное давление изменяет любые характеристики расчета устойчивости уравнения переноса. С учетом капиллярного давления закон Дарси можно выразить в виде Уравнение переноса не изменяет характеристики вследствие наличия капиллярного давления. Эффект капиллярного давления можно включить, изменив гравитационный параметр Cg. В случае, когда суммарная скорость и гравитация имеют разные направления (т.е. фаза 1 с Cg0), капиллярное давление ослабляет гравитационный эффект. Капиллярное давление включает в себя пространственный градиент капиллярного давления (рс), и предполагается, что этот член остается значительно меньшим, чем член вязкостиили гравитационный член Cg. При наличии капиллярной силы можно использовать тот же алгоритм устойчивости, изменив CgIII. Алгоритм для трехфазного потока с учетом гравитации и капиллярного давления. Опишем безусловно устойчивый алгоритм для трехфазного потока с учетом гравитации и капиллярного давления. При моделировании коллектора область трехфазного потока весьма ограничена в модели, и чаще трехфазная область в модели возникает вследствие объединения двух двухфазных потоков. В результате неочевидно, что лабораторные измерения трехфазной относительной проницаемости можно непосредственно применять к моделированию коллектора. Кроме того, измерения трехфазной относительной проницаемости технически очень сложны, M.J. Oak, L.E. Barker и D.C. Thomas, Three-phase relative permeability of Brea sandstone, J. Pet. Tech., стр. 1057-1061, 1990. Для данных неопределенностей в экспериментальных измерениях и проблем масштабирования относительных проницаемостей блоков сетки в модели коллектора, для анализа устойчивости применяется простая модель относительных проницаемостей на основе степенной зависимости. Изучим общие характеристики кривых фракционного потока для трехфазного потока. На основании характеристик кривых фракционного потока был разработан безусловно устойчивый алгоритм для трехфазного потока с учетом гравитации и капиллярного давления. Трехфазный поток Трехфазный поток в пористых средах не вполне изучен вследствие сложности физических явлений и практической трудности измерения трехфазной относительной проницаемости. Однако при моделировании коллектора часто можно видеть, что трехфазный поток в ячейке сетки может возникать, в основном, за счет объединения двух двухфазных потоков. Тем не менее, это влечет необходимость применения трехфазных относительных проницаемостей при моделировании коллектора, которые могут быть усредненными значениями двух относительных проницаемостей для систем вода-нефть и нефть-газ. Модифицированный метод Стоуна II часто применяется во многих имитаторах, в которых относительная проницаемость для нефти моделируется сложной функциональной формой Здесь kr0, krw, и krg - относительная проницаемость нефти, воды и газа соответственно; krocw - относительная проницаемость для нефти при насыщенности реликтовой водой; krow - относительная проницаемость для нефти в системе нефть-вода и krog - относительная проницаемость для нефти в системе газвода. Относительные проницаемости воды и газа такие же, как в двухфазной системе. Относительная проницаемость для нефти согласно модифицированному методу Стоуна II оказывается отрицательной для некоторых систем. Скудные экспериментальные данные не позволяют применять сложную нелинейную функциональную форму, например, метода Стоуна II для трехфазной относительной проницаемости. В работе A. Heiba, Three-phase relative permeability, COFRC Technical Memorandum, 1987, предложена линейная интерполяция krow и krog. Для данных неопределенностей в экспериментальных измерениях и проблем масштабирования относительных проницаемостей блоков сетки в модели коллектора, для анализа устойчивости применяется простая модель относительных проницаемостей на основе степенной зависимости. Анализ можно дополнительно распространить на любые подходящие модели трехфазной относительной проницаемости (без отрицательных значений или немонотонных кривых). Сначала рассмотрим трехфазный поток с учетом гравитации. Как и в вышеописанном анализе устойчивости двухфазного потока, капиллярное давление будет включено позже путем изменения гравитационного числа. Закон Дарси для трехфазного потока можно представить в виде Здесь k - проницаемость, u - фазная скорость, kr - относительная проницаемость,- вязкость, D глубина и- плотность. Нижний индекс i обозначает свойства фазы (т.е. i=1, 2, 3 для водной, нефтяной и газовой фазы соответственно). Из уравнения (67) можно легко получить Суммарная скорость определяется как и дробные параметры заданы в виде где mi - отношение вязкостей по отношению к вязкости фазы 1, 1/i. Скорость, обусловленная силой тяжести, характеризуется переменными, Cgi где uc - характеристическая скорость. Заметим, что скорости u и ui в (68)-(70) являются безразмерными величинами, приведенными к uc. Вследствие ограничения на насыщенности только два уравнения в (68)-(70) являются независимыми. Уравнения для u1 и u2 выбраны в качестве независимых уравнений, и также S1 и S2 выбраны в качестве независимых переменных путем замены S3 на 1-S1-S2. Исследуем поверхности фракционного потока из уравнений (68) и (69) Для примера выберем типичные отношения подвижностей, m2=0,2 и m3=10 и квадратичные относительные проницаемости На фиг. 20 и 21 поверхности фракционного потока построены без учета гравитации (Cg1-Cg2=0) и с учетом сильной гравитации (Cg1=5 и Cg2=10) соответственно. Кривые фракционного потока монотонны для малых Cg1 и Cg2, тогда как они могут стать многозначными функциями для больших Cg1 и Cg2. Заметим, что в зависимости от направлений силы тяжести и скорости, фракционный поток может быть меньше нуля или больше единицы. Это может привести к численной трудности, если метод нелинейных итераций Ньютона не учитывает фактическую картину этих поверхностей. Из (68) и (69) можно вывести граничные кривые, где фракционный поток становится равным нулю Для квадратичных относительных проницаемостей уравнения (85) и (86) принимают вид Анализ устойчивости Как отмечено выше, вопросы устойчивости нелинейных задач переноса заключаются в линеаризации функции плотности потока. Проверим численные схемы на предмет их сходимости от начальной оценки насыщенности Кроме того, после каждой итерации требуется, чтобы 0Sj+11. Поверхности фракционного потока Теперь рассмотрим поверхности фракционного потока, чтобы понять их общие характеристики. На фиг. 22, 23 и 24 изображены изолинии фракционного потока для трех случаев отсутствия гравитации(Cg1=Cg2=0), слабой гравитации (Cg1=0,5 и Cg2=1) и сильной гравитации (Cg1=0,5 и Cg2=10) соответственно. Кроме того, для этого графика применяются m1=0,2 и m3=10. В отсутствие гравитации фракционный поток для каждой фазы движется в направлении суммарной скорости. На фиг. 22, где построены изоконтуры фракционного потока от 0,1 до 0,9 с интервалом 0,1, нет областей отрицательного потока. Заметим,что большая область с малой насыщенностью фазой один и два имеет очень слабые фракционные потоки(0,1). При слабой гравитации, как во втором случае, область отрицательного потока для фазы 1 и 2 становится меньше, и абсолютная величина фракционного потока также уменьшается. В положительном фракционном потоке, показанном на фиг. 23 и 24, изолинии фракционного потока построены от 0 до 0,8 с интервалом 0,2; но в области отрицательного фракционного потока для каждой фигуры используются отдельные значения контуров (-0,2, -0,4, -0,6, -0,8, -1, -2) для фиг. 23 А, (-0,05, -0,1, -0,15, -0,2, -0,25, -0,3) для фиг. 23 В, (-0,02, -0,04, -0,06, -0,08, -1, -2) для фиг. 24 А и (-0,05, -0,1, -0,15) для фиг. 24 В. Также построены контуры для u1=0 (верхняя пунктирная линия) и u2=0 (нижняя пунктирная линия). Вследствие сложного поведения контурных кривых в области отрицательного потока, якобиан уравнения (91) может оказаться сингулярным. Геометрические места особых точек, где детерминант якобиана, Det, равен нулю, также обозначены сплошными линиями. Успешный безусловно устойчивый алгоритм должен учитывать особые точки якобиана, поскольку общий итерационный метод Ньютона не может пересекать эти линии сингулярности. Можно построить границы нулевого фракционного потока для фазы 1 (F1=0) и фазы 2 (F2=0) Из уравнений (93) и (94) можно получить точку пересечения с осью S2=0. Эти точки обозначаютсяS11 из (92) и S11 из (93) соответственно. На этих кривых нулевого потока заданы две точки (S11,S21) и(S12,S22) для улучшения начальной оценки насыщенности, которая используется в алгоритме, описанном ниже. Точка показана в середине области для F10, F20 и Det0 (S13,S23) (т.е. (0,3, 0,3) на фиг. 24 А).- 15014117 Алгоритм обновления SS+1 в трехфазном потоке с учетом гравитации и капиллярного давления 1. Проверить направления суммарной скорости и силы тяжести; 2. Вычислить Cg1 и Cg2; 3. Вычислить границы нулевого фракционного потока для фазы 1 (L1(S1,S2) и L2(S1,S2); 4. Вычислить начальные точки для насыщенности (S11,S21) и (S12,S22) на L1(S1,S2) и L2(S1,S2) соответственно; 5. Проверить знак F1 и F2; 6. Из начальной оценки насыщенностей (S10 и S20) вычислить оценку фракционного потока (F10 и(a) если первоначальная гипотеза насыщенности не удовлетворяет условию положительности, взять точку на L1(S11,S21) в качестве первоначальной гипотезы;(b) итерировать насыщенности на основании уравнения (91);(c) если F10 или F20, задать насыщенность на L1(S11,S21); вычислить нижнюю релаксацию итерации насыщенности, т.е. S+1=(S+S+1)/2; 8. Если F10, F20 и Det0, задать начальную оценку насыщенности в точке на L1(S11,S21) в качестве первоначальной гипотезы; 9. Если F10, F20 и Det0 или F10, F20 и Det0, задать начальную оценку насыщенности в точке L1(S12,S22) в качестве первоначальной гипотезы; 10. Если F10, F20 и Det0, задать начальную оценку насыщенности в точке (S13,S23) в качестве первоначальной гипотезы. Альтернативный алгоритм для трехфазной устойчивости При моделировании трехфазного потока как комбинации двух областей двухфазного потока (т.е. областей газ-нефть и нефть-вода) алгоритм устойчивости можно модифицировать следующим образом. Доля области двухфазного потока и их насыщенности (например, фазы газ-нефть и нефть-вода) определяются из аппроксимаций трехфазной относительной проницаемости (например, насыщенность нефтью однородна в двух областях или относительная проницаемость для нефти одинакова в двух областях). Анализ устойчивости для двухфазного потока применяется для каждой области в итерациях НьютонаРафсона. Если в одной из двух областей происходит неустойчивое изменение насыщенности, применяется процедура нижней релаксации, чтобы гарантировать устойчивую сходимость итераций НьютонаРафсона. Капиллярное давление В многофазном потоке в пористых средах флюидам свойственно находиться под разными давлениями вследствие различия их способности к смачиванию породы и межфазного натяжения между флюидами. Это капиллярное давление часто моделируют простой функцией насыщенности. В трехфазном потоке мы имеем две независимые кривые капиллярного давления Капиллярное давление определяет микроскопические потоки в порах, но играет подчиненную роль при моделировании коллектора. Предполагается, что капиллярное давление изменяет любые характеристики расчета устойчивости уравнения переноса. С учетом капиллярного давления закон Дарси можно выразить в виде Заметим, что уравнение переноса не изменяет характеристики вследствие наличия капиллярного давления. Эффект капиллярного давления можно включить, изменив гравитационный параметр Cg. В случае, когда суммарная скорость и гравитация имеют разные направления (т.е. фаза 1 с Cg0), капиллярное давление ослабляет гравитационный эффект. Поскольку капиллярное давление включает в себя пространственный градиент капиллярного давления (pc), предполагается, что этот член остается значительно меньшим, чем член вязкостиили гравитационный член Cg. При наличии капиллярной силы можно использовать тот же алгоритм, описанный в разделе II, видоизменив Cg ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ моделирования имитатора коллектора посредством решения нелинейной S-образной функции F=(S), которая выражает свойство S в физической системе подземного коллектора с имеющимся потоком флюида, причем S-образная функция имеет точку перегиба Sc и заранее определенное значение F, к которому сходится (S), способ содержит этапы, на которых:a) выбирают начальное значение S+1 как возможное решение функции (S),b) применяют итерационный метод Ньютона (Т) к функции (S) в S для определения значения следующей итерации S+1,c) определяют, располагается ли S+1 с противоположной стороны точки перегиба Sc относительноS,d) задают S+1=Sl модифицированной новой оценке, если S+1 располагается с противоположной стороны точки перегиба (S) относительно S+1,e) определяют, удовлетворяет ли S заранее определенному критерию сходимости,f) задают S=S+1, если S+1 не удовлетворяет заранее определенному критерию сходимости,g) повторяют этапы (b)-(f), пока S+1 не будет удовлетворять заранее определенному критерию сходимости, иh) выбирают S в качестве удовлетворительного решения S для S-образной функции F=(S),i) используют удовлетворительное решение S для S-образной функции (S) для моделирования потока флюида в пределах подземного коллектора посредством имитатора коллектора. 2. Способ по п.1, в котором модифицированную новую оценку Sl задают как Sl=S+(1-)S+1, где 01. 3. Способ по п.2, в котором 0,30,7. 4. Способ по п.2 или 3, в котором =0,5. 5. Способ по п.1, в котором модифицированную новую оценку Sl задают равной Sc, точке перегиба функции (S). 6. Способ по любому одному из пп.1-5, в котором S-образная функция (S) является функцией фракционного потока, используемой в имитаторе коллектора для представления характеристик потока флюида в пределах подземного коллектора. 7. Способ по любому одному из пп.1-6, в котором S-образная функция (S) математически согласуется с математическим выражением где S - насыщенность первой фазы в задаче потока двух флюидов,(S) - функция насыщенности S,- 17014117 1 - вязкость флюида в первой фазе и 2 - вязкость флюида во второй фазе. 8. Способ по любому одному из пп.1-7, в котором S+1 удовлетворяет заранее определенному критерию сходимости, если где- заранее определенный предел допуска. 9. Способ по любому одному из пп.1-7, в котором S+1 удовлетворяет заранее определенному критерию сходимости, если где- заранее определенный предел допуска. 10. Способ по любому одному из пп.1-7, дополнительно содержащий этап, на котором задают S+1 равным верхнему или нижнему пределу Sb, если Sv+1 превышает эти пределы на этапе (b). 11. Способ по любому одному из пп.1-10, в котором S-образную функцию F=(S) задают посредством одного из поисковой таблицы или общей аналитической функции. 12. Способ по любому одному из пп.1-11, в котором обновляют ньютоновую итерацию, если функция фракционного потока (S) связана с двухфазным потоком в физической системе подземного коллектора с учетом гравитации в ячейке сетки имитатора коллектора, причем обновление отличается тем, что:(a) проверяют направления фазных скоростей и силы тяжести в ячейке сетки,(b) если фазные скорости сонаправлены, применяют обычный анализ устойчивости Ньютона,(i) вычисляют направленные фракционные потоки Fh и F и их производные второго порядка (Fh" и F"),(ii) вычисляют Cg для вертикального потока (для горизонтального потока Cg=0),(iii) применяют предел насыщенности 0S+11,(vi) если Fh(SV+1)Fh(SV)0 или F"(S+1)F"(S)0, применяют нижнюю релаксацию для итерации насыщенности,(c) если фазные скорости противонаправлены,(i) вычисляют точку отражения насыщенности, Sr,(ii) применяют предел насыщенности, если ячейка не соседствует с границей, или соседняя ячейка не принадлежит другой области насыщенности, 0S+1Sr или SrS+11, иначе 0S+11,(iii) если Fh(S+1)Fh(S)0 или F(S+1)F(S)0, применяют нижнюю релаксацию для итерации насыщенности иd) используют обновленную ньютоновую итерацию для моделирования двухфазного потока флюида в пределах подземного коллектора посредством имитатора коллектора. 13. Способ по любому одному из пп.1-11, в котором обновляют ньютоновую итерацию, если функция фракционного потока (S) связана с трехфазным потоком физической системы подземного коллектора с учетом гравитации в ячейке сетки имитатора коллектора, причем обновление отличается тем, что:(a) проверяют направления суммарной скорости и силы тяжести,(b) вычисляют Cg1 и Cg2,(c) вычисляют границы нулевого фракционного потока для фазы 1, (L1(S1,S2 и L2(S1,S2),(d) вычисляют начальные точки для насыщенности, (S11,S21) и (S12,S22) на L1(S1,S2) и L2(S1,S2) соответственно,(e) проверяют знак F1 и F2,(f) из первоначальной оценки насыщенностей (S10 и S20) вычисляют оценку фракционного потока 0(F1 и F20) и детерминант матрицы Якоби,(g) если F10 и F20,(i) если первоначальная оценка насыщенностей не удовлетворяет условию положительности, берут точку на L1(S11,S21) в качестве первоначальной оценки насыщенностей,(ii) итерируют насыщенности на основании причем после каждой итерации применяется ограничение 0Sj+11;(iii) если F10 или F20, задают насыщенность на L1(S11,S21);(v) если или вычисляют нижнюю релаксацию итерации насыщенности,(h) если F10, F20 и Det0, задают первоначальную оценку насыщенностей в точке на(i) если F10, F20 и Det0 или F10, F20 и Det0, задают первоначальную оценку насыщенностей в точке L1(S12,S22);(j) если F10, F20 и F10, F20, задают начальную оценку насыщенности в точке (S13,S23) и(k) используют обновленную ньютоновую итерацию для моделирования трехфазного потока флюида в пределах подземного коллектора посредством имитатора коллектора. 14. Устройство для хранения программ, считываемое машиной, материально выполняющее программу, состоящую из команд, выполняемых машиной, для осуществления этапов способа моделирования имитатора коллектора посредством решения нелинейной S-образной функции, F=(S), которая выражает свойство S в физической системе подземного коллектора с имеющимся потоком флюида, причемS-образная функция имеет точку перегиба Sc и заранее определенное значение F, к которому сходитсяa) выбирают начальное значение S как возможное решение функции (S),b) применяют итерационный метод Ньютона (Т) к функции (S) в S для определения значения следующей итерации S+1,c) определяют, располагается ли S+1 с противоположной стороны точки перегиба Sc относительно S,d) задают S+1=Sl модифицированной новой оценке, если S+1 располагается с противоположной стороны точки перегиба (S) относительно S,e) определяют, удовлетворяет ли Sv+1 заранее определенному критерию сходимости,f) задают S=S+1, если S+1 не удовлетворяет заранее определенному критерию сходимости,g) повторяют этапы (b)-(f), пока S+1 не будет удовлетворять заранее определенному критерию сходимости,h) выбирают S+1 в качестве удовлетворительного решения S-образной функции F=(S) иi) используют удовлетворительное решение S-образной функции (S) для моделирования потока флюида в пределах подземного коллектора посредством машины.
МПК / Метки
МПК: G06F 17/11
Метки: способ, коллектора, устройство, моделирования, имитатора
Код ссылки
<a href="https://eas.patents.su/30-14117-sposob-i-ustrojjstvo-dlya-modelirovaniya-imitatora-kollektora.html" rel="bookmark" title="База патентов Евразийского Союза">Способ и устройство для моделирования имитатора коллектора</a>
Предыдущий патент: Микрожидкостное устройство для идентификации, количественного определения и аутентификации латентных маркеров
Следующий патент: Способ и устройство ввода данных в установку для выполнения операции, связанной с животными
Случайный патент: Липосомы, включающие радиоактивный изотоп, и цитотоксический агент для комбинированной терапии