Способ, система и устройство для обновления модели коллектора в реальном времени с использованием множественного фильтра калмана

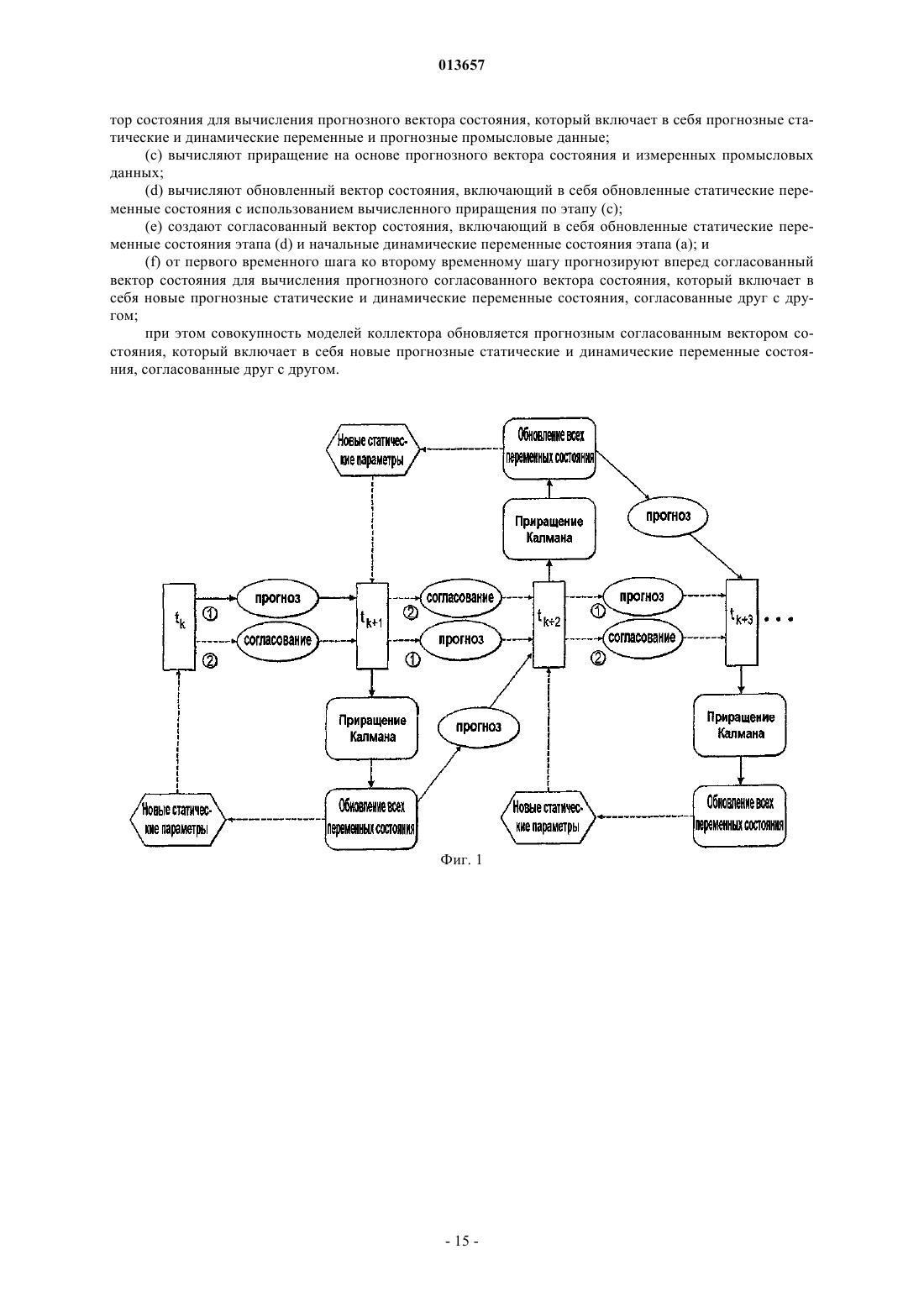
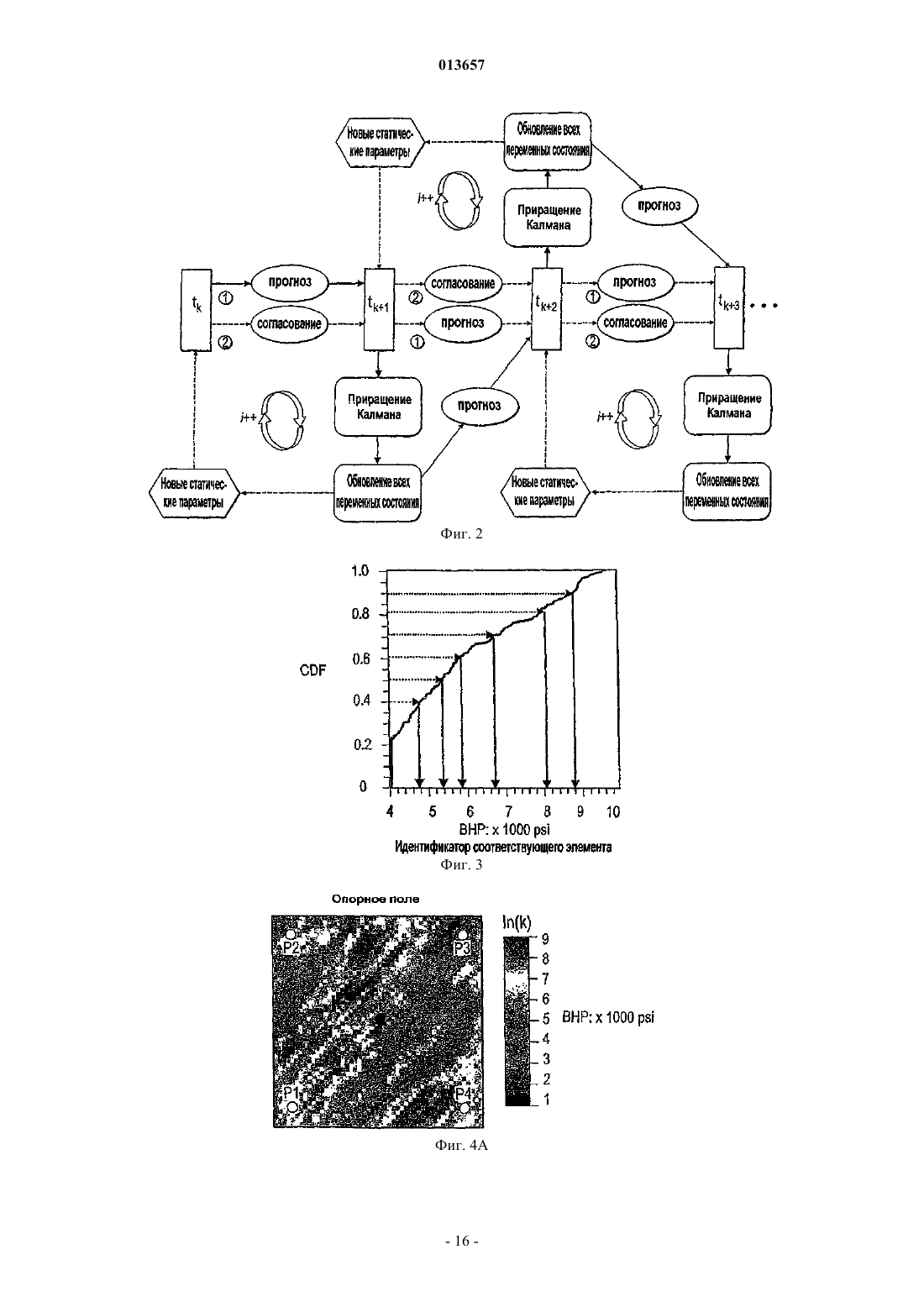
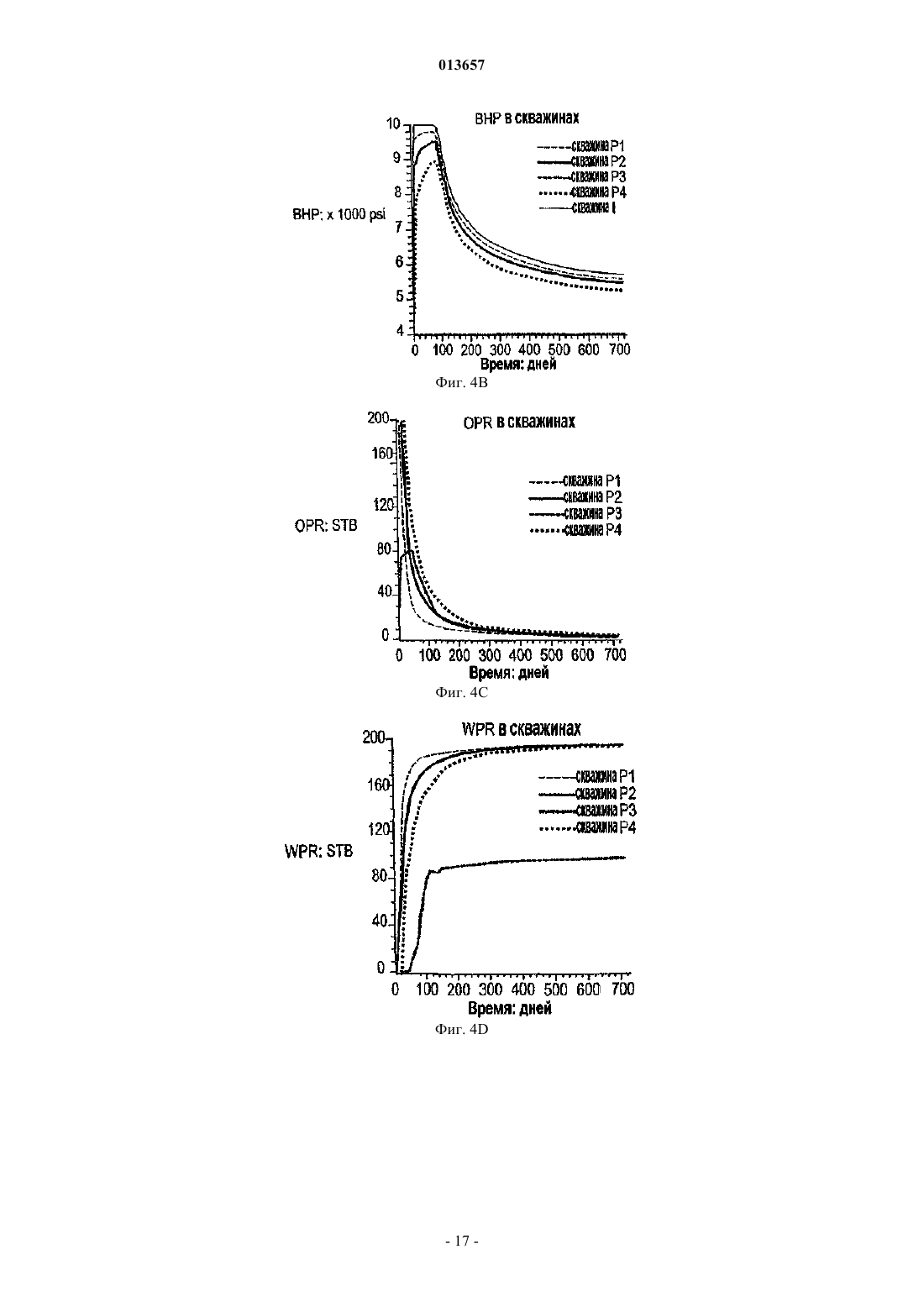
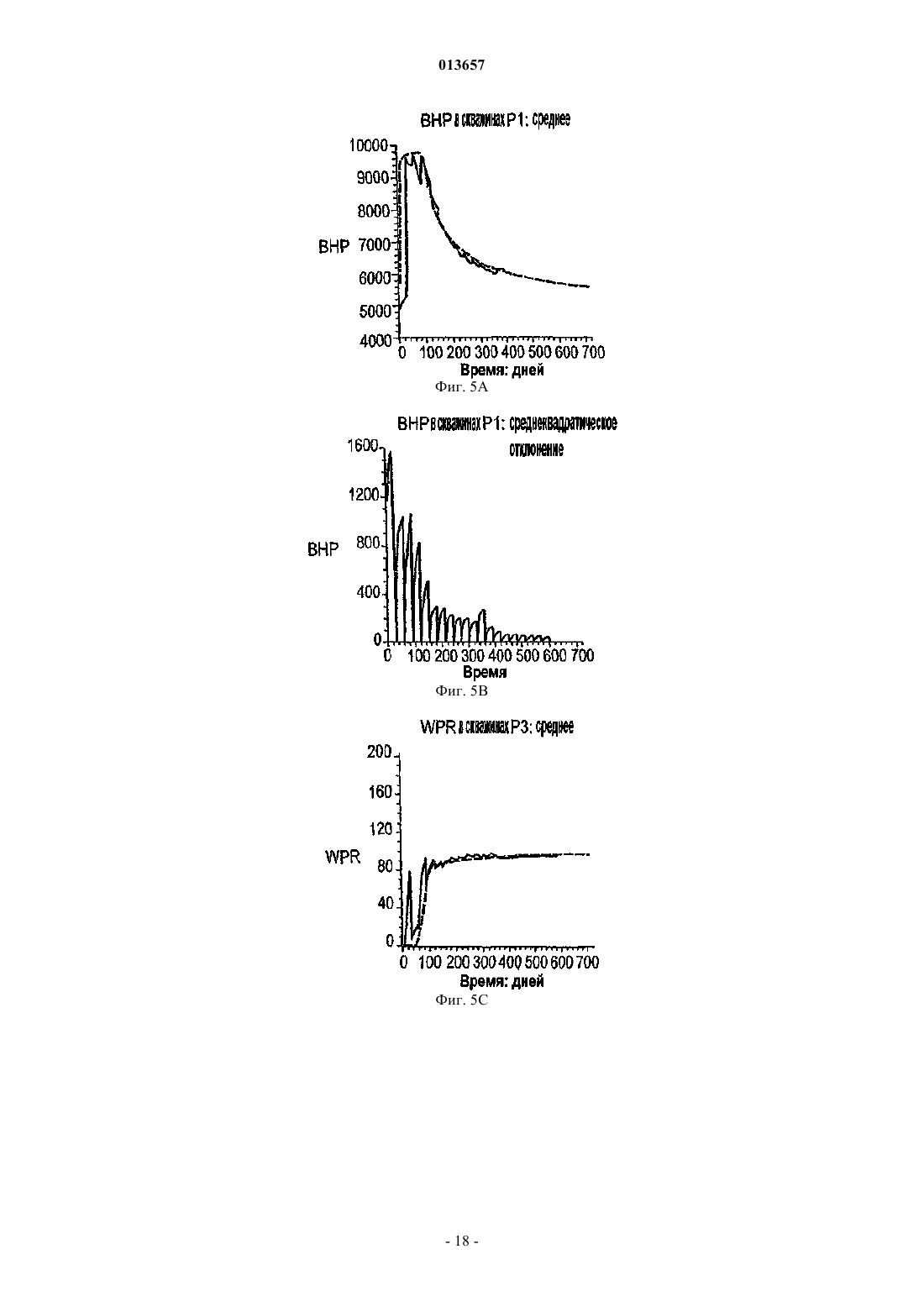
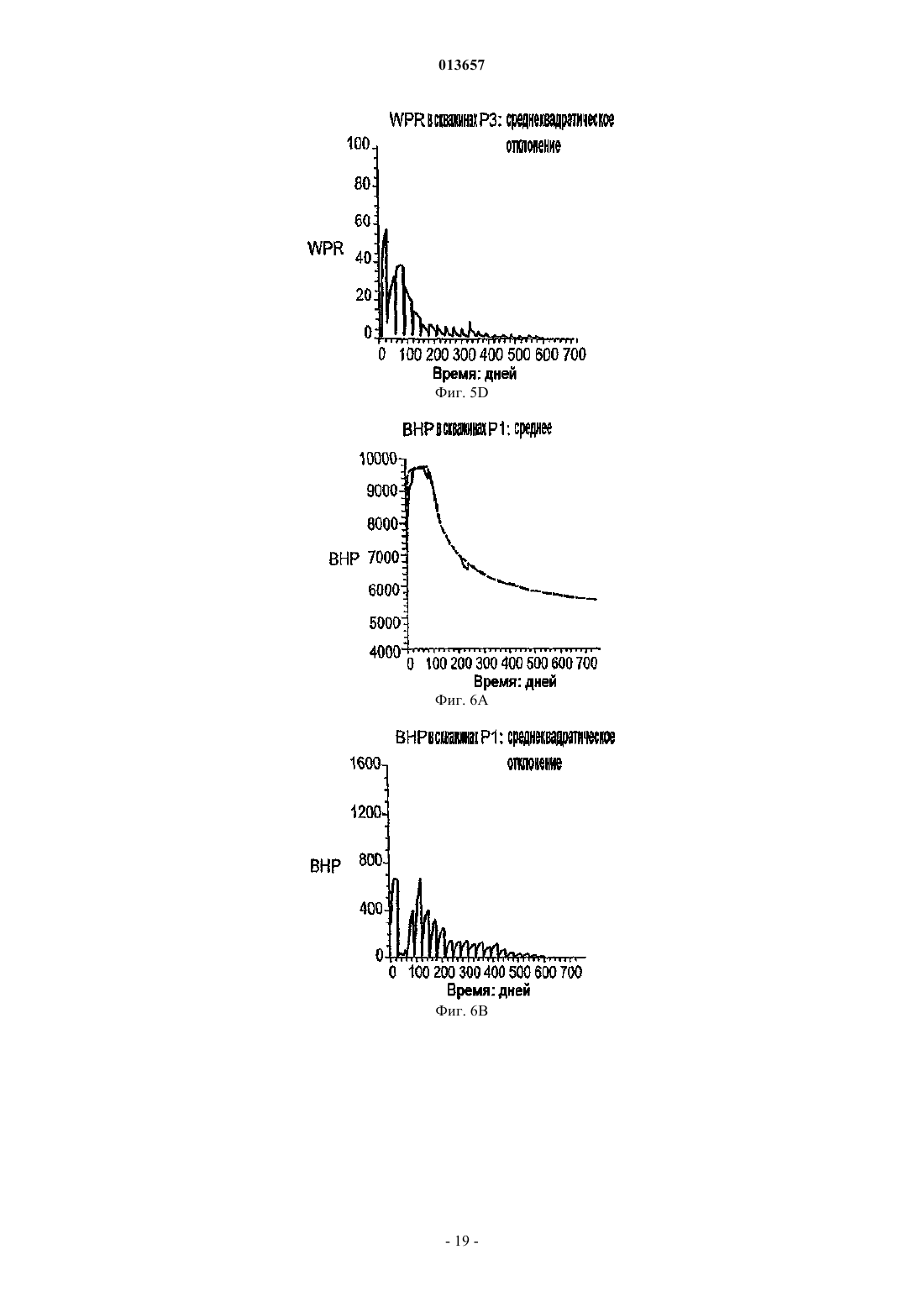
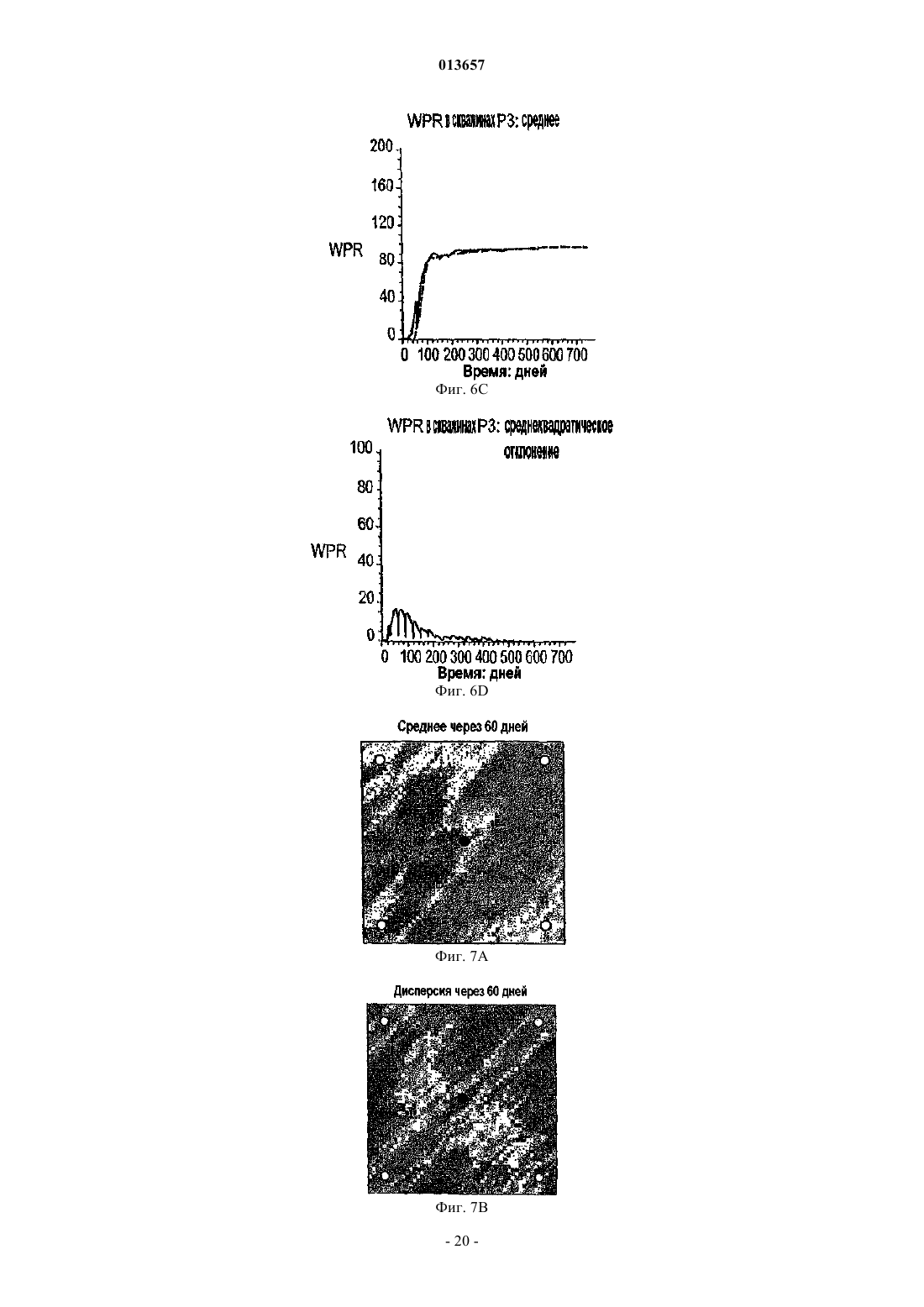
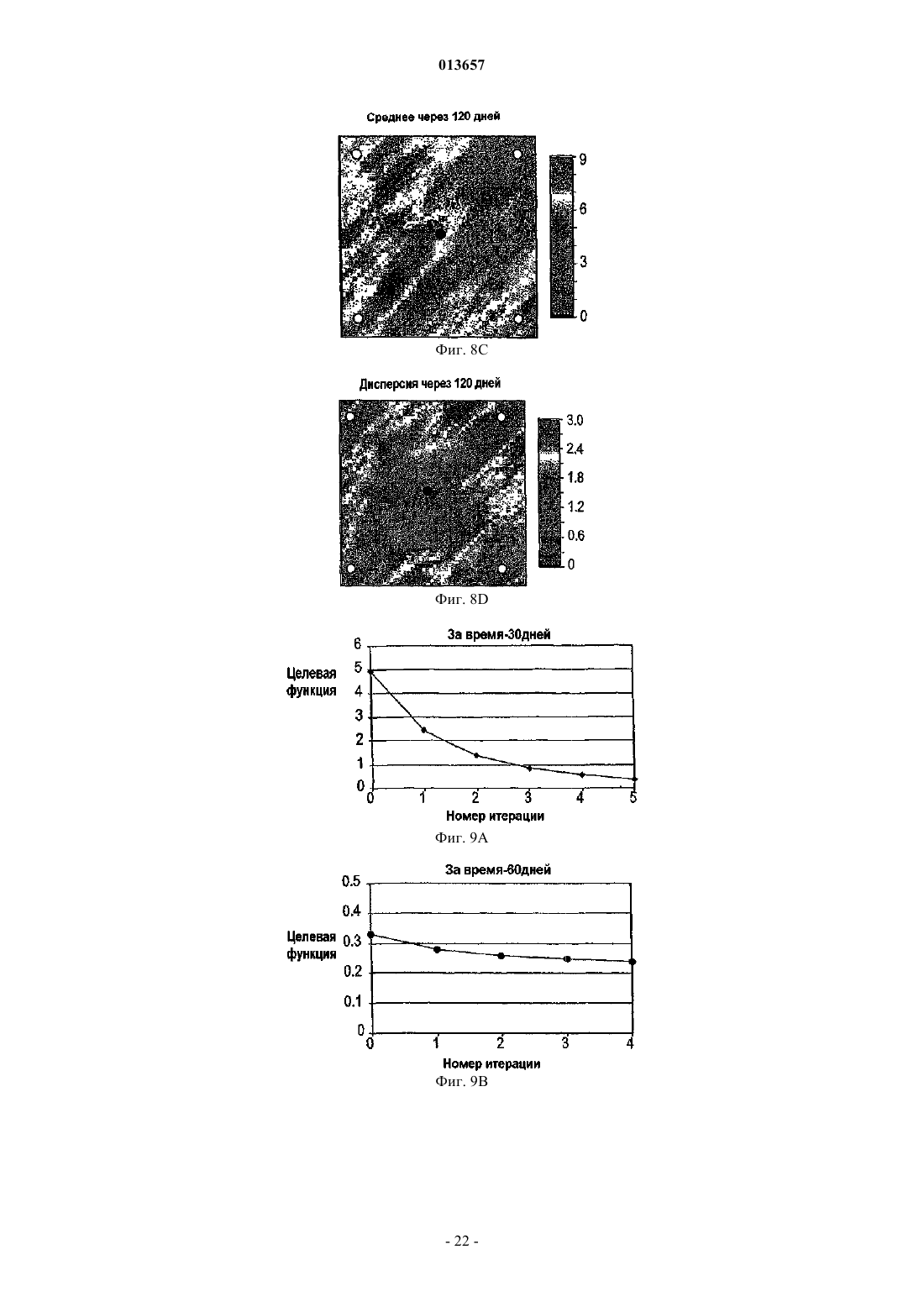
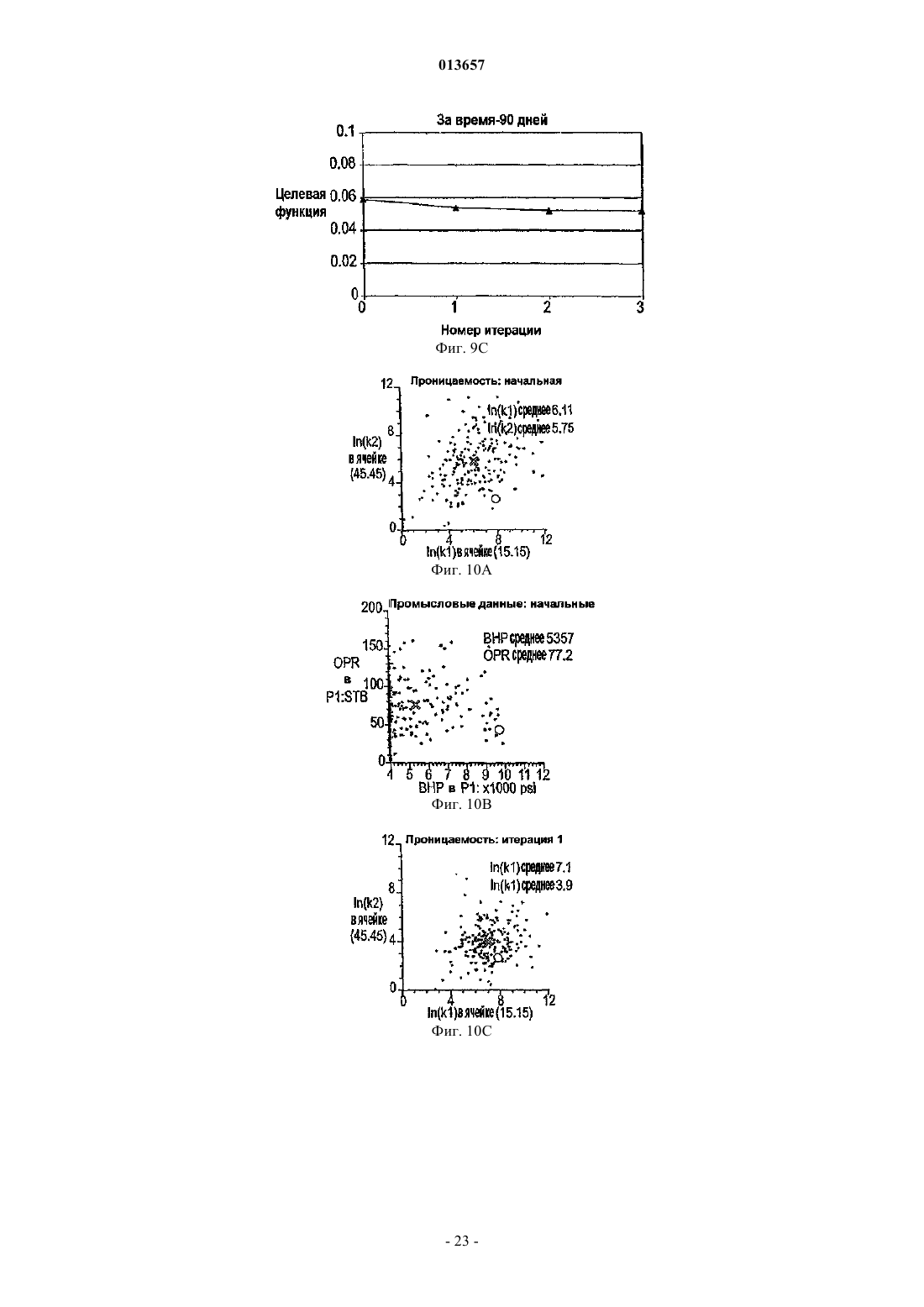
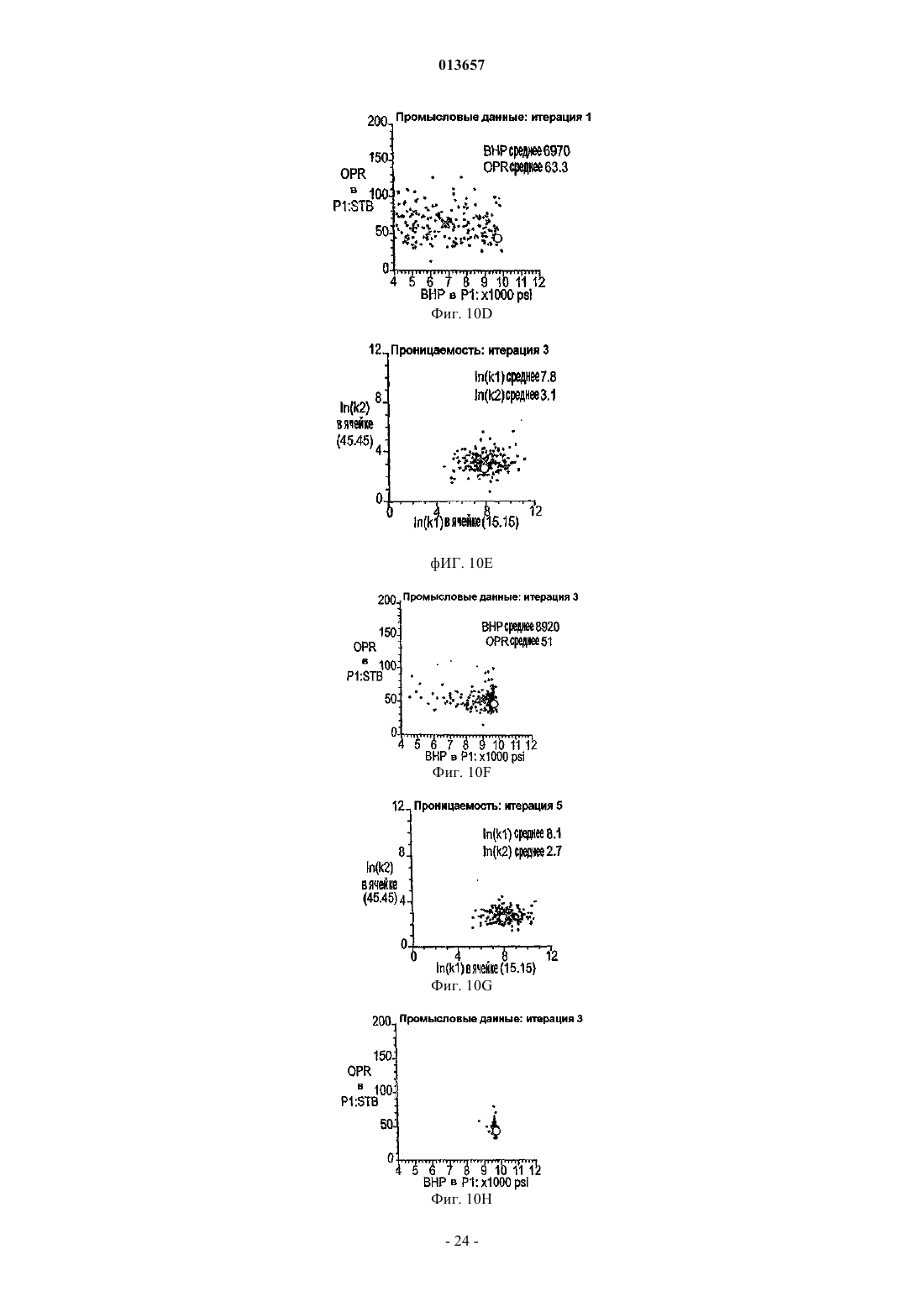
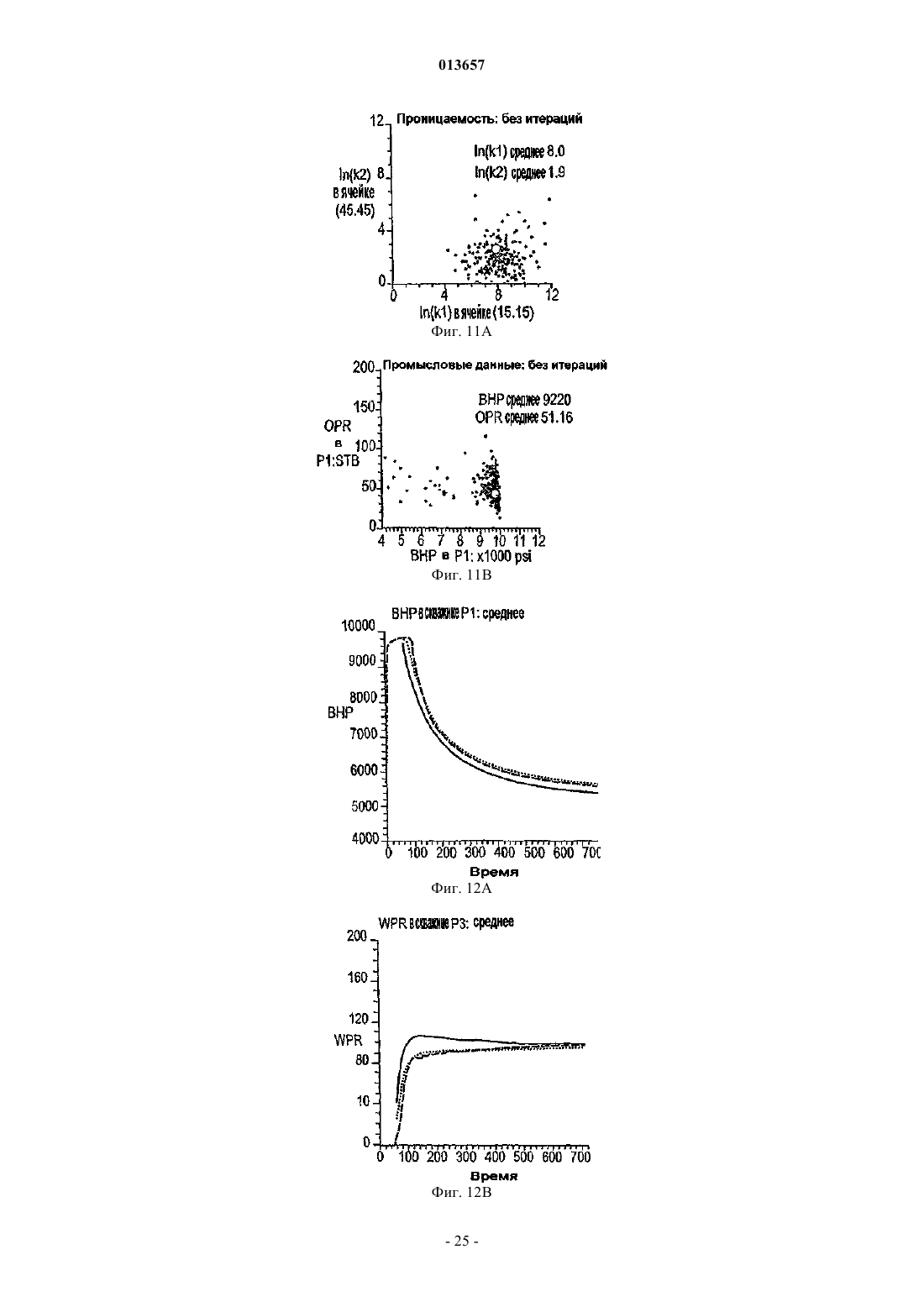
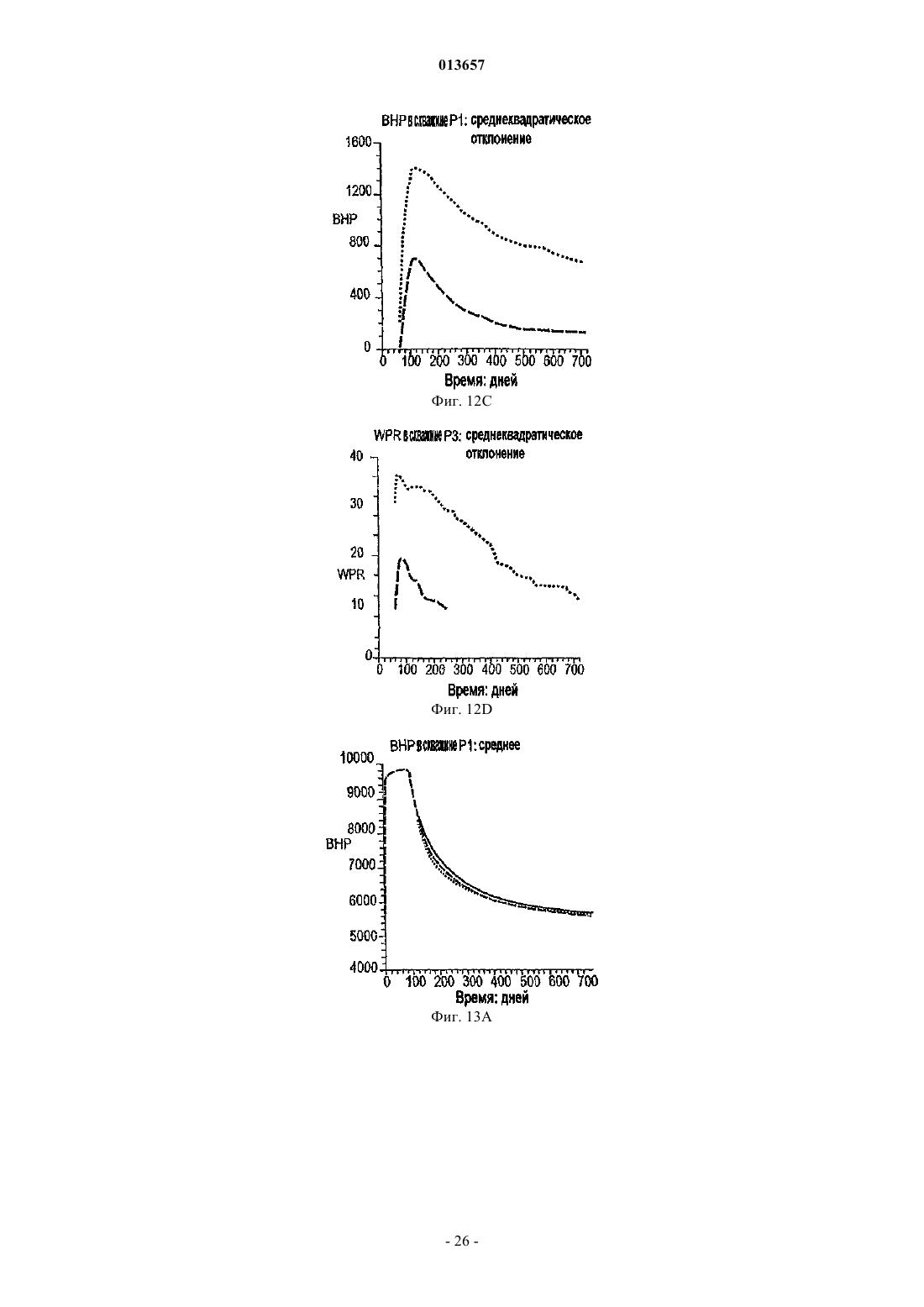
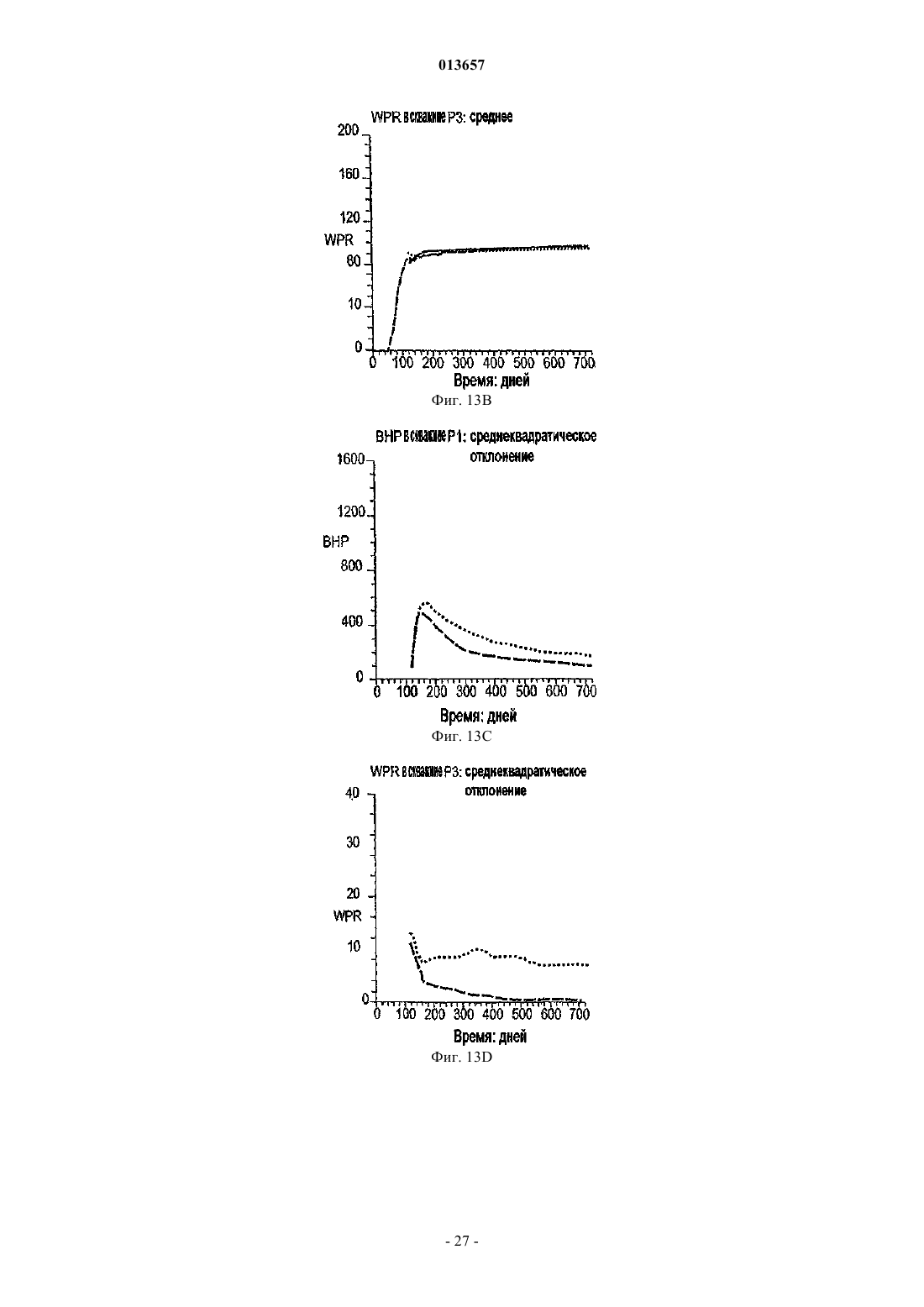
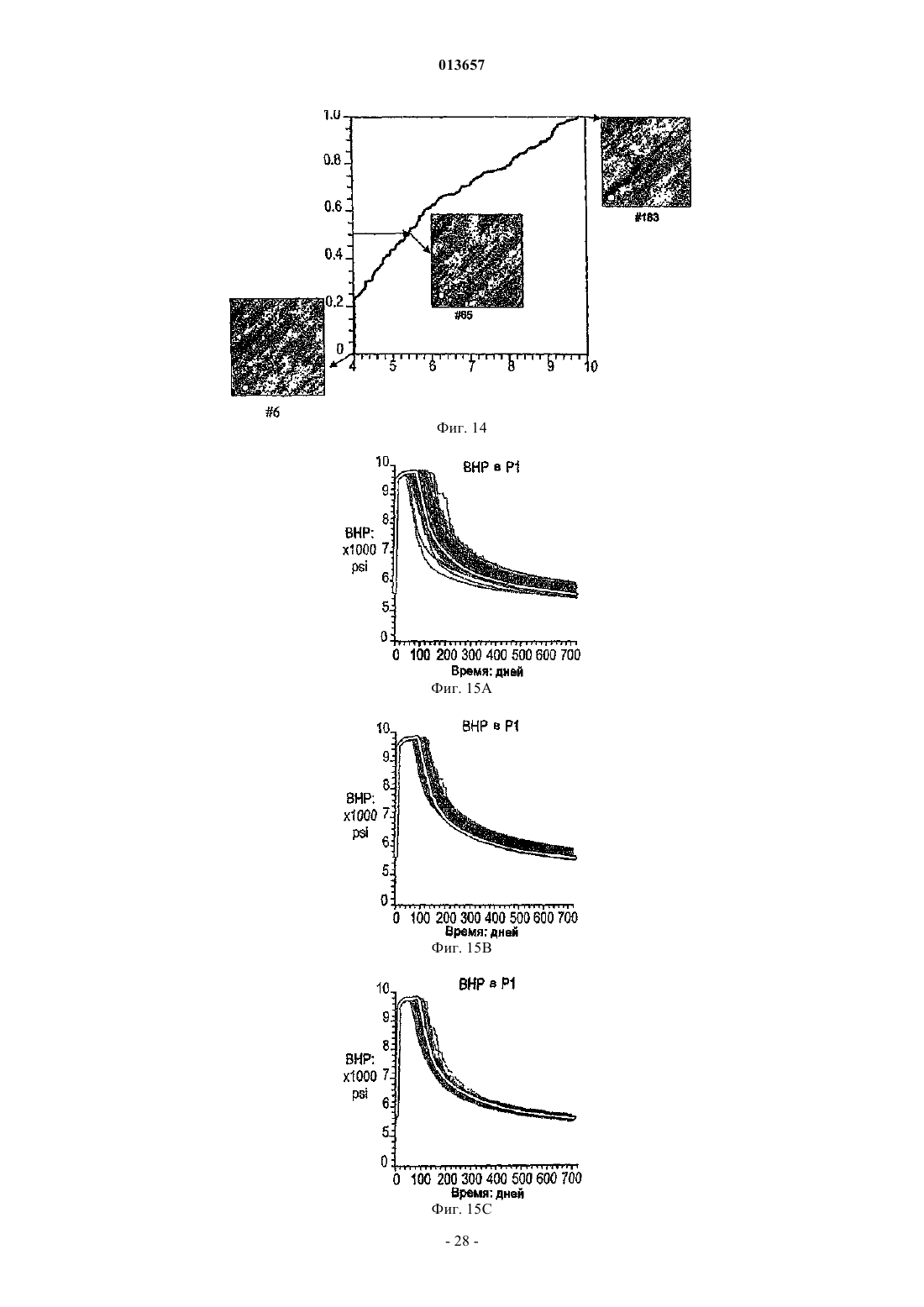
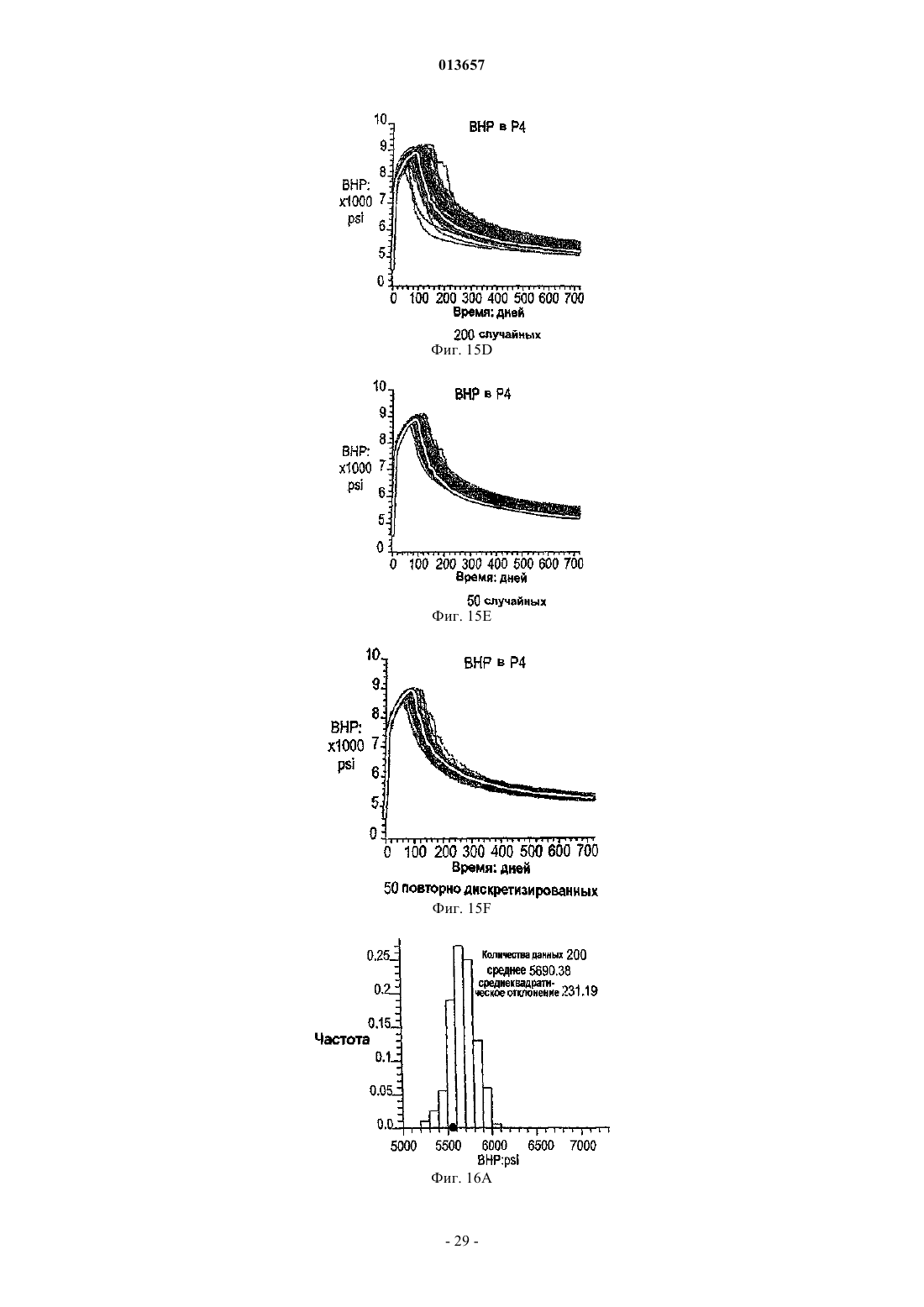
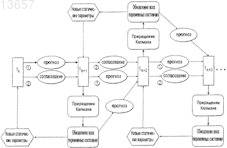
013657 Область техники, к которой относится изобретение Настоящее изобретение в общем относится к средствам моделирования коллектора (нефтеносного или газоносного пласта) для прогнозирования потока текучих сред через подземные пласты, а более конкретно - к способам обновления моделей средств моделирования коллектора так, чтобы иметь совместимость с фактическими измеренными промысловыми данными, с использованием множественных фильтров Калмана (EnKF - ансамбль фильтров Калмана). Уровень техники Модели коллектора стали важной частью анализа принятия текущих решений, связанных с управлением месторождениями нефти/газа. Концепция управления коллектором в "замкнутом контуре" в настоящее время привлекает серьезное внимание в нефтяной промышленности. Метод обновления модели коллектора "в реальном времени" или "непрерывно" является важным компонентом подходящего применения любого процесса управления коллектором в замкнутом контуре. Этот метод должен позволять быстро и непрерывно обновлять модели коллектора, ассимилируя актуальные измеренные промысловые данные, с тем, чтобы прогнозируемые рабочие характеристики и ассоциированная неопределенность были актуальными для вычислений оптимизации. Концепция управления коллектором в замкнутом контуре дает возможность принятия решений в реальном времени, которые максимизируют потенциальный дебит коллектора. Эти решения основаны на самой свежей информации, доступной по модели коллектора, и ассоциированной неопределенности информации. Одним важным требованием в процессе управления коллектором на основе модели в реальном времени является возможность быстро оценивать модели коллектора и ассоциированную неопределенность, отражающие самые свежие промысловые данные в реальном времени. Традиционно проверка достоверности моделей коллектора в сравнении с промысловыми данными осуществляется посредством процесса согласования статистических данных (НМ). Традиционные способы согласования статистических данных испытывают один или более следующих недостатков:(1) промысловые данные для всех статистических данных согласовываются в одно и то же время, и требуются повторяющиеся моделирования потоков для всех статистических данных, что делает НМ очень трудоемким;(2) градиентные способы НМ требуют вычислений коэффициентов чувствительности и минимизации, которые являются сложными, требуют больших ресурсов ЦП и зачастую прерываются локальными минимумами и(3) оценивать неопределенность с помощью традиционных способов является затруднительным и может повлечь за собой повторение процесса согласования статистических данных с различными начальными моделями (это делается редко вследствие времени, связанного с достижением согласования статистических данных). Таким образом, несмотря на значительный прогресс, достигнутый в науке и на практике, традиционные способы согласования статистических данных не являются оптимальными для обновления моделей в реальном времени. Это особенно актуально, когда доступен большой объем данных (к примеру, от постоянных датчиков) и требуется быстрое обновление множества моделей. Способ обновления с помощью множественного фильтра Калмана (EnKF) является оптимальным для таких приложений в сравнении с традиционными способами согласования статистических данных. Уникальные признаки множественного фильтра Калмана обобщены ниже:(1) EnKF пошагово обновляет модели коллектора, собирая и обрабатывая промысловые данные последовательно во времени по мере того, как они становятся доступными, тем самым она идеально подходит для приложений реального времени;(2) совокупность моделей коллектора, которые отражают самые свежие промысловые данные, всегда сохраняется. Таким образом, прогнозируемые рабочие характеристики и неопределенность всегда доступны для анализа оптимизации;(3) EnKF является вычислительно быстрым благодаря эффективности параллельного/распределенного вычисления;(4) EnKF может быть применен в любом средстве моделирования коллектора без необходимости сложного кодирования и(5) EnKF не требует оптимизации и вычисления коэффициентов чувствительности. Эти признаки делают EnKF идеальным для обновления моделей коллектора в реальном времени. С момента своего появления EnKF широко использовался в метеорологии и океанографии для сбора и обработки данных в крупных нелинейных системах. Evensen, G.: "Sequential data assimilation with aDynamics, 53 (4), 343-367, 2003. Множественный фильтр Калмана недавно был внедрен в нефтяную промышленность. Gu, Y. и"Reservoir monitoring and continuous model updating using ensemble Kalman filter", Доклад SPE 84372,представленный на 2003 SPE Annual Technical Conference and Exhibition, Denver, CO, 5-8 октября, 2003 г. Множественный фильтр Калмана также может быть использован для метода сопоставления статистических данных. Gu, Y. и Oliver, D.S.: "History matching of the PUNQ-S3 reservoir model using theProblem Theory: Methods for Data Fitting and Model Parameter Estimation", Elsevier, Amsterdam,Netherlands, p. 613, 1987. Тем не менее современные методы EnKF имеют ряд недостатков. Во-первых, традиционный EnKF не может разрешить уравнения потока после обновления фильтров Калмана, так что обновленные статические и динамические переменные могут быть несогласованными, т.е. решения уравнений потока на основе обновленных статических переменных могут отличаться от обновленных динамических переменных. Во-вторых, традиционные способы EnKF не могут учитывать нелинейность и другие допущения,сделанные в ходе обновления Калмана. Дополнительно, традиционный EnKF типично требует больших размеров совокупности, чтобы обеспечить точность. Настоящее изобретение разрешает эти недостатки в традиционных способах EnKF. Сущность изобретения Настоящее изобретение представляет способ, систему и устройство для обновления моделей коллектора в реальном времени с помощью множественного фильтра Калмана. Способ содержит следующие этапы. Генерируется совокупность моделей коллектора. Совокупность представляется на первом временном шаге посредством начального вектора состояния статических и динамических переменных состояния. Например, статические переменные состояния могут включать в себя пористость и/или проницаемость. Динамические переменные состояния могут включать в себя давление и насыщение. От первого временного шага ко второму временному шагу начальный вектор состояния прогнозируется вперед,чтобы вычислить прогнозный вектор состояния, который включает в себя прогнозные статические и динамические переменные и прогнозные промысловые данные. Приращение, предпочтительно приращение Калмана, вычисляется на основе прогнозных переменных состояния и прогнозных промысловых данных. Обновленный вектор состояния обновленных статических и динамических переменных состояния далее вычисляется с помощью вычисленного приращения, а также наблюдаемых промысловых данных и прогнозных промысловых данных. Затем создается согласованный вектор состояния, включающий в себя обновленные статические переменные состояния и динамические переменные состояния. В завершение,от первого временного шага ко второму временному шагу согласованный вектор состояния прогнозируется вперед, чтобы вычислить прогнозный согласованный вектор состояния, который включает в себя прогнозные статические и динамические переменные состояния. Соответственно совокупность моделей коллектора обновляется статическими и динамическими переменными состояния прогнозного согласованного вектора состояния, согласованными друг с другом. Также может быть использован способ итеративного демпфирования вместе с этапом согласования, чтобы учитывать нелинейность в общей обратной задаче посредством внешней итерации с обновлением демпфирования. Дополнительно предусмотрен способ, который уменьшает размер совокупности моделей коллектора, которые должны быть обновлены. Цель настоящего изобретения заключается в том, чтобы предоставить способ согласования статических и динамических переменных моделей коллектора с использованием способа обновления множественного фильтра Калмана. Другая цель заключается в том, чтобы предоставить способ множественной фильтрации Калмана, в котором итерации используются для того, чтобы корректировать гауссовы и линейные допущения в системе. Еще одна другая цель заключается в том, чтобы предоставить метод дискретизации для выбора поднабора совокупностей из большого размера совокупностей, что обеспечивает точность при снижении числа совокупностей, требуемых для того, чтобы точно выполнять EnKF.-2 013657 Краткое описание чертежей Фиг. 1 - это схематичный чертеж неитеративной процедуры множественного фильтра Калмана(EnKF) (согласно сплошным стрелкам) и процесса согласования EnKF (согласно толстым стрелкам и пунктирным стрелкам (1), затем (2. Фиг. 2 - это схематичный чертеж итеративного процесса EnKF (согласно процессу согласованияEnKF) с итерациями, выполняемыми в ходе этапов обновления. Фиг. 3 - это график кумулятивной функции распределения (cdf) давления забоя скважины (ВНР) и однородной дискретизации членов модели и cdf. Фиг. 4A-4D иллюстрируют опорное поле проницаемости и графики промысловых данных. Фиг. 5A-5D иллюстрируют графики среднего (слева) и среднеквадратического отклонения (справа) ВНР в первой эксплуатационной скважине Р 1 и водопритока (WPR) в третьей эксплуатационной скважине Р 3 с помощью неитеративного процесса обновления EnKF. Фиг. 6A-6D иллюстрируют графики среднего (слева) и среднеквадратического отклонения (справа) ВНР в Р 1 и WPR с помощью итеративного процесса обновления EnKF. Фиг. 7A-7D иллюстрируют среднее и дисперсию 200 моделей проницаемости, обновляемых через 60 и 120 дней с помощью неитеративного процесса обновления. Пунктирные линии - это результаты из достоверной модели. Фиг. 8A-8D иллюстрируют среднее и дисперсию 200 моделей проницаемости, обновляемых через 60 и 120 дней с помощью итеративного процесса обновления. Фиг. 9A-9C - это графики изменения целевой функции в ходе итерации в различное время сбора и обработки. Фиг. 10A-10 Н - это графики значений проницаемости, обновляемых посредством итеративногоEnKF при различных итерациях и соответствующих промысловых данных, вычисленных из обновленных моделей проницаемости. Крестики представляют среднее 200 моделей, а пустые точки являются достоверными/наблюдаемыми значениями. Фиг. 11A, 11B - это графики значений проницаемости, обновляемых посредством неитеративногоEnKF через 30 дней, и промысловых данных, вычисляемых из обновленных моделей проницаемости. Крестики представляют среднее 200 моделей, а пустые точки являются достоверными/наблюдаемыми значениями. Фиг. 12A-12D иллюстрируют графики среднего (вверху) и среднеквадратического отклонения (внизу) промысловых данных, спрогнозированных с помощью моделей проницаемости, обновляемых через 60 дней; пунктирные линии соответствуют достоверным данным, сплошные линии являются результатами неитеративного EnKF, точечные линии являются результатами итеративного EnKF. Фиг. 13A-13D иллюстрируют графики среднего (вверху) и среднеквадратического отклонения (внизу) промысловых данных, спрогнозированных с помощью моделей проницаемости, обновляемых через 120 дней; пунктирные линии соответствуют достоверным данным, сплошные линии являются результатами неитеративного EnKF, точечные линии являются результатами итеративного EnKF (отметим повышение точности и снижение неопределенности в сравнении с результатами фиг. 12). Фиг. 14 иллюстрирует кумулятивную функцию распределения (cdf) наиболее изменяющейся переменной (ВНР в эксплуатационной скважине Р 1). Фиг. 15A-15F иллюстрируют графики смоделированных промысловых данных для всех статистических данных с помощью обновленных моделей на последнем временном шаге (720 дней) при различных начальных наборах совокупностей; белые линии являются достоверными результатами. Фиг. 16A-16C иллюстрируют гистограммы спрогнозированного давления забоя скважины (ВНР) в эксплуатационной скважине Р 1 через 720 дней от обновленных моделей на последнем временном шаге при различных начальных наборах совокупностей (жирные точки являются достоверными результатами). Фиг. 17A-17 Н иллюстрируют среднее и дисперсию 200 моделей проницаемости, обновляемых через 300 дней при другом интервале t времени сбора и обработки с помощью неитеративной схемы обновления EnKF. Фиг. 18A-18 Н иллюстрируют среднее и дисперсию 200 моделей проницаемости, обновляемых через 300 дней при другом интервале t времени сбора и обработки с помощью итеративного EnKF. Фиг. 19A-19 Н иллюстрируют графики промысловых данных на основе моделей, обновляемых через 300 дней с помощью неитеративной схемы обновления ENKF. Белые линии соответствуют опорному полю, а точечные линии являются средним прогнозов. Фиг. 20A-20 Н иллюстрируют графики прогнозов промысловых данных на основе моделей, обновляемых через 300 дней с помощью итеративного ENKF. Белые линии соответствуют опорному полю, а точечные линии являются средним прогнозов. Фиг. 21A-21 Н иллюстрируют графики значений проницаемости, обновляемых посредством итеративного EnKF при различных итерациях и соответствующих промысловых данных, вычисляемых из обновленных моделей проницаемости через 200 дней. Крестики представляют среднее 200 моделей, а пус-3 013657 тые точки являются достоверными/наблюдаемыми значениями. Фиг. 22A, 22B иллюстрируют графики значений проницаемости, обновляемых посредством неитеративного EnKF через 300 дней, и промысловых данных, вычисляемых из обновленных моделей проницаемости. Крестики представляют среднее 200 моделей, а пустые точки являются достоверными/наблюдаемыми значениями. Подробное описание изобретения Сначала описывается традиционный метод EnKF. Этот метод соответствует пути, показанному посредством сплошных стрелок на фиг. 1. Далее описывается способ, который приводит в соответствие статические и динамические параметры. Данный способ использует этапы согласования, которые содержатся в традиционном методе EnKF. Дополнительные этапы согласования показаны посредством пунктирных стрелок на фиг. 1. Далее вводится итеративный процесс в метод обновления EnKF, который учитывает возможные гауссовы и нелинейные признаки в системе коллектора, см. фиг. 2. Затем описывается способ повторной дискретизации, который уменьшает размер совокупности моделей коллектора, которые должны быть обновлены. Также исследуется чувствительность использования различных интервалов времени сбора и обработки. Примерный метод EnKF, используемый на практике в соответствии с настоящим изобретением, используется затем согласно синтетическому двумерному примеру, чтобы показать преимущества, которые должны быть достигнуты с помощью аспектов настоящего изобретения. Обновление множественного фильтра Калмана. Обновление EnKF является байесовским подходом и инициализируется посредством формирования начальных моделей коллектора с помощью априорных геостатистических допущений. Промысловые данные вводятся последовательно во времени, и модели коллектора обновляются по мере того, как вводятся новые промысловые данные. Обновление EnKF состоит из трех процессов на каждом временном шаге:(1) прогнозирование на основе текущих переменных состояний (т.е. решение уравнений потока с текущими статическими и динамическими переменными):(3) обновление переменных состояния. Развитие динамических переменных диктуется посредством уравнений потока. Переменные состояния включают в себя три типа переменных: статические переменные (к примеру, поля проницаемости и пористости, которые традиционно называются статическими, поскольку они не изменяются во времени. Тем не менее, в подходе EnKF статические переменные обновляются во времени и тем самым изменяются во времени, представляя получение новой информации из данных. Это понятие "статическое" используется для удобства традиционных принципов); динамические переменные (к примеру, давление и фазовое насыщение всей модели, которые являются решениями уравнений потока) и промысловые данные (к примеру, дебит скважины, давление забоя скважины, угловая скорость добычи/нагнетания, обводненность и т.д., которые обычно измеряются в скважинах). Совокупность переменных состояния моделируется посредством множества реализаций так, что где yk,j - j-й член совокупности для вектора состояния в момент времени tk;d - вектор промысловых данных. В предпочтительном и примерном варианте осуществления ms - проницаемость в каждой ячейке модели коллектора, при этом размерность N является общим числом активных ячеек, md включает в себя давление и водонасыщенность (двухфазная модель) в каждой ячейке (с размерностью 2N), a d включает в себя давление забоя скважины, дебит нефти и дебит воды в скважинах с размерностью Nd,k. Размерность вектора состояния Ny,k может изменяться во времени tk так, чтобы учитывать различные объемы промысловых данных в различные моменты времени. Систему условных обозначений, связанных с уравнениями, используемыми в настоящем описании, можно найти в конце данного подробного описания. Специалистам в данной области техники должно быть понятно, что другие статические, динамические и промысловые переменные и данные, отличные от вышеупомянутых переменных и данных, также могут быть использованы и входят в объем настоящего изобретения. Пошаговый процесс традиционного EnKF описывается следующим образом (см. фиг. 1 согласно сплошным стрелкам). Фильтр инициализируется посредством формирования начальных совокупностей статических и динамических векторов. В начальное время (tk) доступные промысловые данные отсутствуют. Предусмотрено множество способов, которые могут быть использованы для того, чтобы формировать начальную-4 013657 совокупность. В данном примерном варианте осуществления геостатистический способ, такой как последовательное гауссово моделирование, используется для того, чтобы сформировать множество (200) реализаций поля проницаемости с данными статистическими параметрами (гистограмма и вариограмма),чтобы представить начальную неопределенность в модели проницаемости, до того как какие-либо промысловые данные станут доступными. Начальные динамические переменные (т.е. начальное давление и насыщение) считаются известными без неопределенности. Таким образом, динамические переменные являются одинаковыми для каждой реализации. Тем не менее, если начальные переменные также являются неопределенными, они должны быть представлены посредством совокупностей. Последовательное гауссово моделирование дополнительно описано в Deutsch, C.V. и Journel, A.G.: GSLIB: GeostatisticalSoftware Library and User's Guide, вторая редакция, Oxford University Press, New York, p. 369, 1998. Этап прогнозирования запрашивает средство моделирования коллектора, чтобы выполнять прямое моделирование для каждой из реализаций до следующей точки во времени, где новые измерения промысловых данных доступны и должны быть ассимилированы (к примеру, tk+i). Вектор переменных состояния после выполнения прогноза обозначается как yfk=t1,j (отметим, что значения статических переменныхms на начальном и прогнозном этапах одинаковы). Прогнозирование создает совокупность новых динамических и промысловых данных в данное время, согласованных с начальными статическими переменными. Приращение Калмана затем может быть вычислено как где Gk - приращение Калмана для времени tk;Hk - матричный оператор, который связывает вектор состояния с промысловыми данными. Поскольку промысловые данные являются частью вектора состояния, как в уравнении (1), Hk имеет форму Hk=[0/I], где 0 - это матрица Nd,k(Ny,k-Nd,k) со всеми нулями в ее элементах; I - это единичная матрица Nd,kNd,k. Надстрочный индекс f обозначает прогноз, означая то, что значения выводятся из средства моделирования до обновления фильтров Калмана; Cd,k - ковариационная матрица ошибки промысловых данных с размерностью Nd,kNd,k, и она является диагональной, поскольку предполагается, что ошибки промысловых данных являются независимыми; Cfy,k - ковариационная матрица переменных состояния в момент времени tk, которые могут быть оценены из совокупности спрогнозированных результатов (yfk,j) с помощью стандартного статистического способа. В качестве примера, но не ограничения,один такой статистический способ представляется следующим образом: где Yfk - совокупность спрогнозированного вектора состояния в момент времени tk размерностью- среднее переменных состояния, которое является вектором размерностью Ny,k. Специалистам в данной области техники должно быть понятно, что другие статистические способы также могут быть использованы и входят в объем изобретения. С помощью Gk и промысловых данных во временном шаге (dk) ассимиляции вектор переменных состояния далее обновляется следующим образом: Отметим, что случайные возмущения добавляются в наблюдаемые промысловые данные (dk), чтобы создать совокупность набора промысловых данных, где dk,j является j-м членом совокупности.Weather Review, 126, 1719-1724, 1998, показали, что изменчивость среди обновленных членов совокупности слишком мала, если случайный шум не добавляется в промысловые данные. Уравнение (4) имеет очевидный физический смысл: вторая часть второго члена в правой части является разностью моделированных и наблюдаемых промысловых данных; чем больше эта разность, тем большим должно быть обновление, применяемое к начальному вектору состояния. Если моделированные промысловые данные в данной реализации равны наблюдаемым данным, не потребуется выполнение обновлений в этой модели. Ковариационная матрица после обновления может быть вычислена как При этом обновлении вектор состояния каждой реализации в совокупности, как считается, отражает самые свежие промысловые данные (dk) и следующий временной шаг может быть достигнут, где новые промысловые данные доступны для ассимиляции. Переменные состояния продвигаются по времени следующим образом: где F - средство моделирования коллектора. Из уравнений (4) и (5) можно видеть, что обновление совокупности является линейным и имеется базовое допущение, что ошибка модели и ошибка промысловых данных являются независимыми. Кроме того, ошибки модели и промысловых данных не корректируются по времени.-5 013657 Общая последовательность операций EnKF показана на фиг. 1 согласно сплошным стрелкам. Промысловые данные включаются в модели коллектора последовательно во времени по мере того, как они становятся доступными, и совокупность моделей коллектора развивается во времени, представляя ассимиляцию результатов измерений в данное время. Когда получаются новые измерения промысловых данных, несложно смоделировать вперед последовательность операций с помощью самого свежего вектора состояния до времени, когда новые промысловые данные собраны, и выполнить вышеуказанный анализ,чтобы обновить вектор состояния так, чтобы отразить новые данные. Каждая ассимиляция представляет определенную степень приращения качества в оценке модели коллектора. Степень данного приращения зависит от того, сколько информации передают новые измеряемые данные. Таким образом, нет необходимости начинать весь процесс заново с исходного начального времени, чтобы включить новые получаемые данные, тогда как при традиционном согласовании статистических данных статические переменные обрабатываются как статические (неизменяющиеся во времени), и все промысловые данные согласуются одновременно с использованием одного набора статических переменных. Когда имеются новые измерения, которые должны быть согласованы, полное согласование статистических данных должно быть повторено с использованием всех данных. Преимущество использования EnKF очевидно, особенно когда частота данных достаточно высока, как, например, в случае данных от постоянных датчиков.EnKF может быть основан на любом средстве моделирования, поскольку он требует только выходных данных средства моделирования. Средство моделирования выступает как черный ящик в процессеEnKF. Таким образом, кодирование способа EnKF значительно проще, чем традиционные градиентные способы согласования статистических данных, где сложное кодирование вычислений чувствительности требуется для различных средств моделирования, и необходим доступ к исходному коду средства моделирования. Другое преимущество EnKF заключается в том, что он предоставляет совокупность Ne моделей коллектора, которые все ассимилируют актуальные промысловые данные при машинном времени примерно в Ne моделирований движения потока (время ЦП для ассимиляции данных очень мало в сравнении с моделированием потока). Это хорошо подходит для анализа неопределенностей, когда требуется несколько моделей коллектора. Тем не менее при традиционном согласовании статистических данных есть необходимость повторять ресурсоемкий для ЦП процесс согласования статистических данных для различных начальных моделей, чтобы создать несколько моделей. Более того, EnKF оптимально подходит для параллельного/распределенного вычисления, поскольку развитие во времени совокупности моделей коллектора полностью независимо. Традиционный EnKF имеет потенциальную проблему: обновленные динамические переменные md(к примеру, давление и насыщение), использующие уравнения (4), могут не иметь физического смысла и могут быть несовместимыми с обновленными статическими переменными ms (к примеру, проницаемостью) за то же время. Под "несовместимыми" понимается то, что решения уравнений потока с использованием средства моделирования коллектора на основе обновленных статических переменных отличается от динамических переменных, обновляемых посредством фильтра. Это обусловлено тем, что обновление Калмана является линейным, тогда как уравнения потока являются нелинейными. В одном аспекте настоящего изобретения дополнительный этап добавляется к EnKF, который должен быть упомянут как"этап согласования", чтобы обеспечить то, что обновленные динамические и статические переменные являются совместимыми. Способ обновления EnKF с помощью "этапа согласования" проиллюстрирован на фиг. 1, при этом этап согласования показан пунктирными стрелками. Этот способ может выполняться следующим образом:(a) начиная со времени tk вектор текущего состояния yk,j (со статическими и динамическими переменными ms и md) используется для того, чтобы прогнозировать (моделировать вперед) прогнозный вектор состояния yfk,j в следующее время tk+1, который включает в себя статические и спрогнозированные динамические переменные ms, mfd и вектор df прогноза промысла; отметим, что статическая переменнаяms прогнозного вектора состояния уk,о остается неизменной со времени tk, в то время как динамические переменные mfd изменяются вследствие вычисления прогноза;(b) приращение на основе измеренных или наблюдаемых данных d и спрогнозированных промысловых данных df, наиболее предпочтительно приращение Калмана Gk, затем вычисляется с помощью спрогнозированного вектора состояния yfk,j. В идеале, приращение Калмана вычисляется использованием уравнения (2);(c) приращение затем используется для создания обновленного вектора состояния yuk,j, включающего в себя переменные mus и mud; предпочтительно это обновление спрогнозированного вектора состояния(d) статические переменные mus из этапа (с) далее используются для обновления, т.е. замены статических переменных ms в исходном векторе состояния yk,j, чтобы создать обновленный вектор состоянияy'k,у, включающий в себя обновленные статические переменные mus и исходные динамические переменные md; и(e) прогнозирование согласования выполняется с использованием обновленного вектора состоянияy'k,j во время tk, чтобы сформировать согласованный вектор состояния yck,j во время tk+1.-6 013657 Этот согласованный вектор состояния yck,j во время tk+1 затем используется для начала следующего этапа ассимиляции. Посредством добавления этого этапа согласования к традиционной методологии обновления совокупностей Калмана обеспечивается то, что обновленные статические и динамические переменные совместимы с уравнениями движения потока. Ценой этого является удвоение времени ЦП в сравнении с традиционным EnKF без согласования. Тем не менее этот этап согласования зачастую является желательным, и улучшенные результаты получаются, в частности, для времени, когда есть существенные изменения промысловых данных, к примеру когда добавляются новые скважины или когда они закрываются. Обновленный с помощью уравнения (4) вектор состояния является оптимальной линейной несмещенной оценкой (оценкой с наименьшей дисперсией). Таким образом, он является линейным обновлением. Базовое допущение этого обновления состоит в том, что ошибки вектора состояния и ошибки наблюдения являются несмещенными и некоррелированными. Кроме того, обновленный вектор состояния(yuk,j) может быть выражен как линейная комбинация начального вектора состояния (yfk,j) и вектора наблюдения (dk), который минимизирует апостериорную дисперсию. Присущее допущение во всех фильтрах Калмана состоит в том, что ошибки на этапе анализа являются гауссовыми. Тем не менее на практике уравнения движения потока и измеренные данные могут не удовлетворять этим допущениям. В другом аспекте настоящего изобретения вводится подход, чтобы учитывать нелинейность в общей обратной задаче посредством внешней итерации для обновления демпфирования. Этот процесс внешней итерации вводится в рамках этапа обновления EnKF, чтобы уменьшить эффекты возможных некорректных допущений (см. фиг. 2). Обновление на каждой итерации следующее:(a) начиная с текущего времени tk прогнозирование (моделирование вперед) до следующего времени (tk+1) с помощью текущего вектора состояния;(b) вычисление приращения Калмана на основе получающихся результатов прогнозирования (т.е. с помощью уравнения (2;(c) обновление только статического параметра (т.е. с помощью формулы, аналогичной уравнению(4, но с включенным коэффициентом демпфирования где aik - параметр демпфирования в момент времени tk на итерации i со значением от 0 до 1;yu,i+1k,j - обновленный вектор состояния в момент времени tk на итерации i+1;yu,ik,j - обновленный вектор состояния в момент времени tk на итерации i;Gik - приращение Калмана на i-й итерации;dik,j - наблюдаемые промысловые данные в момент времени tk на i-й итерации;Hk - матричный оператор, который связывает вектор состояния с промысловыми данными в векторе состояния в момент времени tk; иyf,ik,j - спрогнозированный вектор состояния в момент времени tk на i-й итерации;(d) принятие новых обновленных статических параметров ms (т.е. проницаемости и пористости) и выполнение моделирования потока от текущего (т.е. tk) до следующего момента времени (tk+1) повторно;(e) вычисление целевой функции (среднего и дисперсии всех элементов), которой предпочтительно является нормализованный квадратный корень разности между наблюдаемыми и моделируемыми промысловыми данными; и(f) если среднее и дисперсия целевой функции не меньше заранее заданных значений, возврат к началу алгоритма на этапе а). В противном случае, если среднее и дисперсия целевой функции достаточно малы или когда уменьшение целевой функции слишком мало, осуществляется переход к следующему этапу ассимиляции. Новый обновленный статический параметр и согласованные динамические переменные используются в качестве исходного/начального вектора состояния для следующего этапа ассимиляции. Параметр демпфирования "aik" предпочтительнее всего выбирается посредством метода проб и ошибок для различных задач. В качестве примера, но не ограничения этот параметр демпфирования также может быть выбран равным 0,5 в качестве начального значения. Специалистам в данной области техники должно быть понятно, что другое средство выбора параметра демпфирования также может быть выбрано и входит в объем. Обновленные статические переменные используются для того, чтобы повторно вычислять обновленные динамические переменные и прогнозные данные, из которых вычисляется целевая функция. Целевая функция представляет разность между наблюдаемыми и моделируемыми промысловыми данными. В качестве одного примера целевая функция вычисляется как нормализованный квадратный корень средней разности между наблюдаемыми и моделируемыми данными. Итерация продолжается до тех пор,пока целевая функция не станет достаточно мала, т.е. в рамках заранее определенных критериев, или когда уменьшение целевой функции слишком мало. Типично эти критерии могут быть установлены, к примеру, как 10% от значения целевой функции на начальном этапе или на предыдущем этапе.-7 013657 Данный итеративный процесс обновления проверяется и описывается ниже с помощью примера так, чтобы проиллюстрировать его влияние на результаты. Это улучшение итерации требуется только тогда, когда возникают существенные изменения поведения потока, например, в начале времени отбора или когда новые скважины добавляются либо закрываются. В большинстве других периодов сбора и обработки дополнительные итерации не требуются. Критерий того, использовать или нет эти итерации в следующее время ассимиляции, может быть задан и автоматически применен в ходе процесса сбора и обработки. Более того, для случаев, когда расстояние между моделируемыми и измеряемыми значениями большое, традиционное обновление EnKF может приводить к проблемам вследствие линейного допущения. Использование дополнительных итераций позволяет снижать нелинейные эффекты и тем самым снижать расходимость фильтра. Расходимость фильтра означает процесс, при котором обновленные статические переменные существенно отклоняются от достоверных или ранее обновленных стабильных значений.EnKF - это метод Монте-Карло, который основан на применении большого набора совокупностей для того, чтобы вычислять требуемую статистику, а также производную неопределенность. Вычислительная эффективность EnKF тем самым сильно зависит от размера совокупности, используемой в вычислении. Слишком малый размер совокупности приводит к большой ошибке дискретизации для вычисления ковариационных функций, требуемых для обновления EnKF, и может вызывать расходимость фильтра. Исследования показали, что относительно большой размер совокупности требуется для надежной оценки неопределенности прогнозирования. Один подход для того, чтобы повысить эффективностьEnKF, заключается в том, чтобы улучшить начальную дискретизацию элементов, так чтобы меньшее число элементов могло предоставлять максимальный охват пространства неопределенности, приводя к более стабильному обновлению фильтров. Известны методы дискретизации данной произвольной переменной для эффективного вычисления распространения неопределенности, к примеру, полиномиальное хаотическое разложение или метод вероятностной коллокации. Xiu, D., Karniadaskis, G.E.: "Modeling uncertainty in flow simulations viageneralized polynomial chaos", Journal of Computational Physics, 187, 137-167, 2003. Было оценено применение этих методов для оптимальной инкапсуляции информации, содержащейся в переменных входного случайного поля и выходного случайного движения потока (Sarma, P., Durlofsky, L.J., Aziz, K. и Chen,W.H.: "Efficient real-time reservoir management using adjoint-based optimal control and model updating",Computational Geosciences, 2005). Эти методы требуют, чтобы случайные переменные были независимыми, тем самым требуется методология представления пространственно коррелированной случайной функции посредством последовательности независимых случайных переменных, к примеру разложение Карунена-Лоэва (L-K) (Reynolds, А.С., Не, N. Chu, L. и Oliver, D.S.: "Reparameterization techniques forgenerating reservoir descriptions conditioned to variogram and well-test pressure data", SPE Journal, 1, 413-426,1995). Данный тип операции обычно является вычислительно медленным для крупной системы, поскольку он требует вычисления собственных значений и собственных векторов. В работе Evensen, G.: "Sampling strategies and square root analysis schemes for the EnKF", OceanDynamics 54, 539-560, 2004, предложен алгоритм для повторной дискретизации меньшего числа элементов из исходного большего набора совокупностей, с тем чтобы статистика выборок, введенных посредством исходного крупного набора совокупностей, сохранялась. Показано, что этот метод может предоставлять большее пространство неопределенности, чем из того же числа элементов совокупности посредством случайной дискретизации предыдущей cdf, и может предоставлять стабильный характер изменения фильтров. Dong, Y., Gu, Y. и Oliver, D.S.: "Quantitative use of 4D seismic data for reservoir description:the ensemble Kalman filter approach", согласно Journal of Petroleum ScienceEngineering, 2005. Этот метод тем не менее требует разложения по сингулярным значениям (SVD), которое является вычислительно интенсивным для крупных систем. Кроме того, повторная дискретизация служит для воспроизводства статистики, предоставляемой посредством более крупных элементов начальной совокупности. Таким образом, это не учитывает пространство неопределенности промысловых данных. Подход повторной дискретизации в идеале также должен учитывать пространство неопределенности, охватываемое посредством промысловых прогнозов. Принимая во внимание эту цель, можно использовать простую схему повторной дискретизации, которая базируется на ранжировании крупного исходного набора совокупности. Ранжирование модели основано на наиболее изменяющейся промысловой переменной. Могут быть использованы следующие этапы:(1) в начальный момент времени tk формирование крупного набора совокупности размером NT;(2) прямое моделирование каждой модели до времени первой ассимиляции (tk+1);(3) нахождение наиболее изменяющихся промысловых данных посредством вычисления, к примеру, коэффициента изменчивости для каждых промысловых данных;(4) ранжирование модели NT на основе наиболее изменяющихся промысловых данных и извлечение кривой кумулятивной функции распределения (cdf) на основе ранжирования каждой модели (см. фиг. 3);(5) выборка меньшего числа реализаций (Ne) равномерно из кривой cdf, чтобы получить соответствующую модель (см. фиг. 3); и(6) использование меньшего размера совокупности (Ne) для последующих этапов ассимиляции.-8 013657 Этот подход просто и удобно реализовать в рамках любого EnKF. Посредством этого некоторые начальные модели, которые слишком близки друг другу в отношении своих промысловых характеристик, в сущности, исключаются. Кроме того, промысловые данные используются непосредственно для выбора начальных моделей. Затратами этих процессов являются NT-Ne моделирований движения потока от времени tk до tk+1. Недостаток заключается в том, что дискретизация основана на одних промысловых данных во время первой ассимиляции и тем самым может быть недостаточной для того, чтобы точно представить пространство неопределенности для всей модели. Более сложные методы ранжирования могут быть использованы для того, чтобы повысить эффективность этого подхода. В качестве примера,но не ограничения, эти методы ранжирования могут включать в себя, к примеру, упрощенные физические моделирования потока или моделирование на более грубой сетке моделей. Примеры Фиг. 4 А иллюстрирует двумерное геостатистическое опорное поле (сетка 50501 с размером ячейки 20202 футов). Модель формируется с помощью метода последовательного гауссового моделирования. Ln(k) имеет гауссову гистограмму со средним и дисперсией в 6,0 и 3,0 соответственно. Единицей проницаемости является миллидарси. Вариограмма является сферической в диапазоне 200 и 40 футов в направлении 45 и 135 соответственно. Предполагается, что нагнетательная скважина (I) в центре модели с 4 эксплуатационными (Р 1-Р 4) по 4 углам. Основными признаками этого опорного поля являются:(1) зона высокой проницаемости и зона низкой проницаемости в середине поля;(2) высокая взаимосвязанность между скважиной I и скважиной Р 1;(3) низкая взаимосвязанность между скважиной I и скважинами Р 3 и Р 4. Это опорное поле рассматривается как достоверная модель, и цель заключается в том, чтобы восстановить модели коллекторов на основе промысловых данных реального времени, которые наиболее близки к достоверному полю. Коллектор первоначально насыщен нефтью с постоянным начальным давлением в 6000 psi наверху. Нагнетательная скважина имеет постоянную скорость нагнетания 700 STB/день с максимальным управлением давлением забоя скважины (ВНР) 10000 psi. Все эксплуатационные скважины добывают постоянный общий объем 200 STB/день с минимальным управлением ВНР 4000 psi. Отношение подвижности воды и нефти составляет 10, а кривые стандартной квадратичной относительной проницаемости используются с нулевым остаточным насыщением для нефти и воды. Сжимаемость и капиллярное давление игнорируются. Моделирование движения потока выполняется в течение 720 дней, и результаты ВНР каждой скважины, а также дебиты нефти (OPR) и дебиты воды (WPR) в эксплуатационных скважинах показаны на фиг. 4B-4D. Отметим быстрый прорыв воды и высокие дебиты воды в скважине P1, тогда как для Р 3 прорыв воды очень поздний, с небольшим WPR и ВНР этой скважины падает до минимального управления сразу после добычи вследствие низкой проницаемости вокруг данной скважины, а также низкой связности между данной скважиной и инжектором. Опорное поле проницаемости, а также моделируемые динамические данные (ВНР, OPR и WPR) рассматриваются как достоверные, и предполагается, что измерения ВНР, OPR и WPR в скважинах доступны каждые 30 дней вплоть до 720 дней, и они непосредственно считываются из достоверных данных. Среднеквадратическое отклонение ошибок измерения составляет 3 psi, 1 STB и 2 STB для ВНР,OPR и WPR соответственно. Гауссовы случайные ошибки добавляются в окончательные достоверные промысловые данные, чтобы создать зашумленный набор данных. Вектор возмущений с теми же дисперсиями в качестве ошибок измерения затем добавляется в зашумленные данные, чтобы создать совокупность промысловых данных. Начальная совокупность моделей проницаемости формируется с помощью метода последовательного гауссового моделирования с такой же гистограммой и вариограммой в качестве опорного поля. Предполагается, что здесь нет доступной жесткой проницаемости, т.е. все начальные модели являются безусловными. Условное моделирование может быть использовано, когда есть жесткие и/или гибкие данные проницаемости, и они могут быть сохранены в ходе обновления EnKF. Другие параметры (пористость 0,2, кривые относительной проницаемости, начальное давление 6000 psi и начальная водонасыщенность 0,0) считаются известными без неопределенности. Совокупность из 200 начальных моделей проницаемости вводится в EnKF и обновляется через каждые 30 дней путем сбора и обработки наблюдаемых промысловых данных (ВНР, OPR и WPR) в заданные моменты времени. Итерация в сравнении с отсутствием итерации. Фиг. 5A-5D и 6A-5D иллюстрируют изменения средних промысловых данных (ВНР в Р 1 и WPR в Р 3), при этом время и ассоциированные связанные среднеквадратические отклонения (т.е. неопределенность) из 200 моделей использует традиционный EnKF (без согласования и без итерации) и предложенный итеративный EnKF. Для итеративного EnKF максимум 5 итераций используются с параметром демпфирования =0,5. Можно видеть для традиционного метода EnKF, что прогнозируемые промысловые данные в первое время значительно отклоняются от наблюдаемых данных. Помимо этого, во время каждой ассимиляции EnKF обновляет прогнозируемые данные обратно до наблюдаемых с неопределен-9 013657 ностью, сниженной практически до нуля. По мере того как все больше и больше данных ассимилированы, прогнозные данные становятся все ближе и ближе к наблюдаемым данным все с меньшей и меньшей неопределенностью. Таким образом, все меньшее и меньшее обновление требуется для моделей. Аналогичный феномен наблюдается для итеративного EnKF, за исключением того, что прогнозы в первое время гораздо лучше и неопределенности гораздо меньше. Это указывает на то, что модели, обновленные посредством итеративного EnKF, могут предоставлять более точные прогнозы с меньшей неопределенностью при ассимиляции такого же объема данных, особенно когда ассимилированы только данные начального времени. Средние/усредненные поля проницаемости (т.е. оценка) и ассоциированные связанные поля дисперсии (неопределенность), вычисленные из совокупности через 60 и 120 дней, представлены на фиг. 7 А-7D и 8A-8D для неитеративного и итеративного EnKF. В сравнении с опорным полем на фиг. 4A можно видеть, что результаты с помощью итеративного EnKF немного лучше при фиксации признаков пространственной вариации опорной модели и результирующие модели имеют меньшую неопределенность. Отметим, что 5 итераций вводятся для каждого шага обновления EnKF. Тем не менее в этом примере итерации требуются только на первых трех 3 шагах сбора и обработки (через 30, 60 и 90 дней) с фактическим номером итерации 5, 4 и 2 соответственно. После этапа 3 прогнозируемые промысловые данные находятся достаточно близко к наблюдаемым данным для того, чтобы итерации не требовалось. Вариации целевой функции при каждой итерации в рамках первых трех этапов ассимиляции представлены на фиг. 9 А-9 С. Отметим значительное снижение целевой функции для первого этапа ассимиляции(30 дней), указывающее влияние итерации для начального времени, когда характеристики потока имеют сильные нелинейные признаки и требуется существенное обновление для модели для согласования промысловых данных. Для более позднего времени улучшение согласования данных меньше. Фиг. 10A-10G иллюстрируют диаграммы рассеяния значений проницаемости для двух выбранных позиций (ячейка (15, 15) и ячейка (45, 45) считая от левого нижнего угла) из 200 моделей совокупности после каждой итерации в рамках первого этапа ассимиляции (30 дней). Кроме того, показаны соответствующие диаграммы рассеяния промысловых данных (ВНР и OPR для скважины Р 1). Можно видеть, что первоначально проницаемость и прогнозируемые промысловые данные имеют широкий разброс и центрированы в некорректных местах, проявляя существенную неопределенность и неточность в прогнозах,поскольку нет ассимилированных данных. Кроме того, прогнозируемые промысловые данные, в частности ВНР, не являются нормально распределенными. Посредством ассимиляции промысловых данных за 30 дней с помощью итеративного EnKF значения проницаемости и прогнозируемые промысловые данные постепенно перемещаются в направлении значений достоверной модели и наблюдаемых промысловых значений после каждой итерации. В конце итерации промысловые данные близко согласованы, а значения проницаемости рассеяны вокруг достоверных значений с малой неопределенностью. Отметим,что выбранные две позиции находятся в важных зонах (между скважинами I и Р 1, между I и Р 3), где значения проницаемости являются критически важными для сопоставления промысловых данных. Посредством ассимиляции промысловых данных за 30 дней значения проницаемости в этих двух позициях могут быть хорошо идентифицированы уже с малой неопределенностью. Это дает возможность получения точного распределения проницаемости на последней итерации. Меньшая точность и большая неопределенность должны ожидаться в других позициях (см. фиг. 7, 8). С другой стороны, для неитеративного EnKF модели обновляются только один раз с помощью уравнения (4). Диаграммы рассеяния обновленных проницаемостей для тех же позиций и прогнозируемых промысловых данных из скважины Р 1 представлены на фиг. 11. Можно видеть, что обновленные модели проницаемости, а также прогнозируемые промысловые данные с использованием традиционного одношагового обновления являются менее точными и подвержены большей неопределенности в сравнении с предлагаемым итеративным методом EnKF. Промысловые данные, вычисленные из обновленных моделей, по-прежнему проявляют сильные негауссовские свойства. Затем сравнивается возможность прогнозирования моделей, обновленных традиционным и итеративным EnKF. Циклы прогнозирования выполняются до 720 дней с использованием всех 200 моделей после ассимиляции данных за 60 и 120 дней с использованием двух способов. Фиг. 12A-12D иллюстрируют прогнозы промысловых данных (среднего и среднеквадратического отклонения ВНР в Р 1 и WPR в Р 3) из 200 моделей, обновляемых через 60 дней, тогда как фиг. 13A-13D отображают прогнозы с использованием моделей, обновляемых через 120 дней. Из обоих чертежей можно видеть, что прогнозы с использованием моделей, обновляемых посредством итеративного EnKF, являются более точными и менее неопределенными в сравнении с моделями, обновляемыми посредством неитеративного EnKF. Таким образом, оптимизация коллектора в реальном времени на основе прогнозов из моделей, обновленных посредством итеративного EnKF, вероятно, представляет более оптимальные стратегии добычи для реализации потенциального дебита. Для обоих способов более точные и менее неопределенные прогнозы получаются, когда ассимилировано больше промысловых данных.- 10013657 Уменьшение размера совокупности посредством повторной дискретизации Далее иллюстрируется эффективность предлагаемого простого способа повторной дискретизации,чтобы уменьшить размер совокупности в EnKF. 200 начальных моделей (Nr=200) используются и выполняют прогнозирование вперед от 0 до 30 дней. На основе промысловых данных (ВНР, OPR и WPR) за 30 дней самая изменяющаяся переменная идентифицируется как ВНР в скважине Р 1. Эти начальные 200 моделей ранжируются на основе ВНР в Р 1 от наименьшего к наибольшему значению, приводя к кумулятивной функции распределения (cdf), показанной на фиг. 14A-14F. Отметим, что наименьшее ВНР в Р 1 получается от члена 6 модели, где значения проницаемости вокруг Р 1 низкие, тогда как наибольшее ВНР в Р 1 получается от члена 183 модели, где Р 1 размещается в зоне с высокой проницаемостью, которая тесно связана с инжектором. Из 200 начальных моделей 50 членов дискретизируются с использованием метода равномерной дискретизации на основе cdf, т.е. с интервалом cdf=0,02. Очевидно, что результирующие 50 моделей могут представлять одно пространство неопределенности в отношении ВНР в скважине Р 1 как исходные 200 моделей. Многие модели с характеристиками потока, которые слишком близки друг к другу, исключены. Повторно дискретизированные 50 моделей затем используются для последующего обновленияEnKF. Для сравнения, обновление EnKF выполняется с помощью первых 50 моделей из начальных 200 моделей, представляющих 50 случайно дискретизированных начальных элементов. EnKF затем используется на этапе согласования только для обновления моделей, ассимилирующих те же промысловые данные, что и показанные на фиг. 4. На основе моделей проницаемости, обновленных на последнем временном шаге (720 дней) с использованием различных начальных наборов совокупностей, моделирования потока повторно выполняются для всех промысловых статистических данных с использованием всех обновленных моделей. Фиг. 15A-15F иллюстрируют ВНР для скважин Р 1 и Р 4 с использованием трех различных начальных наборов совокупностей: 200 случайных, 50 случайных и 50 повторно дискретизированных из 200 случайных членов. Гистограммы ВНР в Р 1 через 720 дней отображаются на фиг. 16. Из этих двух чертежей можно видеть, что:(1) 200 случайно дискретизированных членов совокупности представляются достаточными для того, чтобы предоставить разумные прогнозы и ассоциированную связанную неопределенность;(2) 50 случайно дискретизированных членов недостаточны, приводя к точным прогнозам (наблюдаемые промысловые данные находятся вне огибающей прогнозов); и(3) при использовании 50 начальных моделей, повторно дискретизированных из 200 случайных членов, прогнозы являются более точными (среднее прогнозов близко к наблюдению) и имеют меньшее рассеяние в сравнении с использованием 50 случайных членов. Это очевидно демонстрирует эффективность предлагаемого подхода повторной дискретизации, чтобы уменьшить размер совокупности. Влияние интервала времени ассимиляции. Интервал времени между двумя этапами ассимиляции EnKF также является важным вопросом для практического применения EnKF. В общем ассимиляция требуется каждый раз, когда возникают существенные изменения поведения потока, например при добавлении новых скважин в систему коллектора,переоборудовании скважин или закрытии скважин. Промысловые данные могут наблюдаться с другой частотой, и постоянные датчики могут получать данные с очень высокой частотой. Согласно теорииEnKF предпочтительно, чтобы время ассимиляции на интервале было не слишком малым и не слишком большим. Промысловые данные могут быть избыточными и коррелированными, и тем самым никакая новая информация не может усваиваться, когда выбранные точки наблюдаются слишком близко во времени. С другой стороны, если интервал времени ассимиляции слишком большой, параметры модели и промысловые данные могут быть в значительной степени нелинейными, вызывая проблемы обновления фильтра, например расходимость фильтра. Чтобы изучить влияние применения различных размеров интервала времени ассимиляции, EnKF используется для того, чтобы обновить 200 моделей коллектора, ассимилирующих промысловые данные в различные интервалы времени (30, 60, 100 и 300 дней). Используются как неитеративные, так и итеративные методы EnKF. Фиг. 17A, 17B и 18A, 18B показывают результирующее среднее и дисперсию 200 моделей, обновляемых через 300 дней с помощью неитеративного и итеративного EnKF. Прогнозы производительности скважины от 300 дней до 720 дней с использованием моделей, обновляемых через 300 дней, представлены на фиг. 19A, 19B и 20A, 20B. Из этих чертежей можно видеть, что:(1) когда используются небольшие интервалы времени (к примеру, 30 или 60 дней), обновленные модели и ассоциированная неопределенность, а также прогнозы, использующие эти модели, очень похожи вне зависимости от того, используется или нет итерация в обновлении EnKF;(2) когда используются большие интервалы времени (к примеру, 100 или 300 дней), видна существенная разница между результатами с использованием итеративного EnKF и результатами с использованием неитеративного EnKF. Обновленные модели, использующие итеративный EnKF, обычно визуально лучше, чем модели, обновляемые посредством неитеративного EnKF. Прогнозы, использующие модели,обновляемые посредством неитеративного EnKF, подвержены гораздо большей неопределенности, чем прогнозы из итеративного EnKF. Это опять-таки демонстрирует то, что модели, обновляемые посредством итеративного EnKF, предоставляют более точные прогнозы с меньшей неопределенностью; и(3) более важно, при неитеративном EnKF качество обновляемых моделей и прогнозов отражает существенное различие, когда используются различные интервалы времени ассимиляции (см. фиг. 17 и 19). При этом различие в качестве при использовании различных интервалов времени гораздо меньше для итеративного EnKF. Модели, обновляемые посредством неитеративного EnKF, ненадежно предоставляют хорошие прогнозы, когда интервал времени ассимиляции большой. В то же время надежные модели по-прежнему могут быть получены с помощью итеративного EnKF. Хотя нежелательно привязываться к конкретной теории, это может быть обусловлено тем фактом, что использование итерации в EnKF позволяет стабилизировать процесс обновления и корректировать нелинейность. В завершение, показан процесс обновления проницаемости и промысловых данных в ходе первого временного шага ассимиляции с использованием интервала времени 300 дней. Фиг. 21 (верхняя строка) показывает диаграммы рассеяния начальных значений проницаемости в двух местах, а также прогнозируемые промысловые данные (ВНР и OPR в скважине Р 1) через 300 дней из 200 начальных моделей. Можно видеть, что начальная модель и промысловые переменные существенно отличаются от достоверных и наблюдаемых значений с большой неопределенностью. Распределение промысловых данных, в частности, для ВНР показывает негауссовские признаки. С использованием временного шага ассимиляции в 300 дней фиг. 21 (со второй строки до нижней строки) показывает диаграммы рассеяния обновленных значений проницаемости, а также прогнозируемые промысловые данные при различных итерациях от времени первой ассимиляции с использованием итеративного EnKF. Очевидно, что значения проницаемости постепенно перемещаются в направлении достоверных значений, при этом прогнозируемые промысловые данные подходят ближе и ближе к наблюдаемым значениям. В конце итерации получаются превосходные значения проницаемости и промысловые прогнозы, которые очень похожи на результаты, показанные на фиг. 10. Это опять демонстрирует устойчивость итеративного EnKF, т.е. точное обновление и хорошее соответствие промысловых данных может быть получено даже при большом интервале времени ассимиляции. Итерация в рамках обновления EnKF служит в качестве корректирующего процесса для нелинейности и негауссовости. В качестве сравнения с помощью неитеративного EnKF обновленная проницаемость и прогнозируемые промысловые данные на основе обновленных моделей представлены на фиг. 22A, 22B. По сравнению с начальными моделями значения обновленной проницаемости перемещаются ближе к достоверным значениям, приводя к улучшенным прогнозам. Но обновляемые проницаемости по-прежнему подвержены значительной неопределенности, приводя к плохому согласованию прогнозируемых промысловых данных с наблюдаемыми данными вследствие использования большого интервала времени ассимиляции (300 дней). Эти результаты не настолько хороши, как результаты с использованием меньшего интервала времени, показанные на фиг. 11, указывающие чувствительность использования другого размера интервала времени для неитеративного EnKF. Рассмотрены традиционные и согласованные EnKF для непрерывного обновления моделей коллектора для ассимилирования промысловых данных реального времени. Представлен процесс итерации в ходе обновления EnKF, так чтобы дополнительно учитывать нелинейность и негауссовость в системе. Введена простая схема равномерной повторной дискретизации, чтобы уменьшить размер совокупности. Эта схема повторной дискретизации использует информацию ранжирования наиболее варьирующихся промысловых данных, вычисляемых на первом этапе ассимиляции, чтобы обеспечить то, что выбранное малое число членов совокупности имеют такой же охват пространства неопределенности относительно выбранных промысловых данных, что и большой первоначальный набор совокупностей. Также исследована чувствительность использования различных интервалов времени ассимиляции. Из вышеприведенного примера могут быть сделаны следующие выводы:(1) EnKF является эффективным и надежным для обновления коллектора в реальном времени, чтобы ассимилировать актуальные промысловые данные;(2) традиционный неитеративный EnKF, на который влияют нелинейные и негауссовские признаки в коллекторах и проточных системах, может предоставлять неточное обновление. Результаты также чувствительны к размеру интервала времени ассимиляции;(3) за счет введения итерации в рамках процесса обновления EnKF более точные модели получаются с меньшей неопределенностью, приводя к лучшему согласованию промысловых данных и более точным прогнозам. Также процесс обновления фильтров становится более стабильным;(4) итерация требуется только первое время или когда возникают существенные изменения поведения потока, к примеру при добавлении скважин или закрытии скважин. Это моменты времени, когда система демонстрирует сильные нелинейные признаки;(5) предлагаемая схема повторной дискретизации является простой, удобной в реализации, но при этом очень эффективной. Она учитывает поведение потока, что является основным отличием от других способов.Cd - ковариация ошибки промысловых данных; Су - ковариационная матрица вектора состояния;F - средство моделирования потока вперед;G - приращение Калмана; Н - матричный оператор, который связывает вектор состояния с промысловыми данными в векторе состояния;N - общее число активных ячеек в модели коллектора;Nd - размерность вектора промысловых данных;u - обновленный. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ обновления совокупности моделей коллектора для отражения самых свежих измеренных промысловых данных и точного прогнозирования рабочих характеристик коллектора, при этом способ включает в себя этапы, на которых:(a) генерируют совокупность моделей коллектора так, что совокупность представляется на первом временном шаге посредством начального вектора состояния, который включает в себя начальные статические и динамические переменные состояния;(b) прогнозируют от первого временного шага ко второму временному шагу начальный вектор состояния, чтобы вычислить прогнозный вектор состояния, который включает в себя прогнозные статические и динамические переменные состояния и прогнозные промысловые данные;(c) вычисляют приращение на основе измеренных промысловых данных и прогнозных промысловых данных;(d) используют приращение для вычисления обновленного вектора состояния, включающего в себя обновленные статические переменные состояния, причем улучшение характеризуется дополнительным выполнением этапов, на которых:(e) создают согласованный вектор состояния, включающий в себя обновленные статические переменные состояния и начальные динамические переменные состояния; и(f) прогнозируют от первого временного шага ко второму временному шагу согласованный вектор состояния для вычисления прогнозного согласованного вектора состояния, который включает в себя новые прогнозные статические и динамические переменные состояния, согласованные друг с другом; при этом совокупность моделей коллектора обновляется прогнозным согласованным вектором состояния, который включает в себя новые прогнозные статические и динамические переменные состояния, согласованные друг с другом. 2. Способ по п.1, в котором начальные, прогнозные, обновленные и новые прогнозные статические переменные состояния включают в себя по меньшей мере одно из проницаемости и пористости. 3. Способ по п.1 или 2, в котором начальные, прогнозные, обновленные и новые прогнозные динамические переменные состояния включают в себя по меньшей мере одно из давления и насыщения. 4. Способ по пп.1, 2 или 3, в котором приращением является приращение Калмана. 5. Способ по п.4, в котором приращение Калмана вычисляется с помощью следующего математического выражения: где Gk - приращение Калмана для времени tk;Cfy,k - ковариационная матрица прогнозного вектора состояния;Hk - матричный оператор, который связывает прогнозный вектор состояния с вектором промысловых данных в начальном векторе состояния; иCd,k - ковариационная матрица ошибки измеренных промысловых данных. 6. Способ по пп.1-4 или 5, в котором обновленный вектор состояния вычисляется, используя следующее математическое выражение: где yuk,j - обновленный вектор состояния в момент времени tk;Gk - вычисленное приращение на этапе (с), причем приращением является приращение Калмана;dk,j - измеренные промысловые данные в момент времени tk;Hk - матричный оператор, который связывает прогнозный вектор состояния с вектором промысловых данных в начальном векторе состояния;yfk,j - прогнозный вектор состояния. 7. Способ по пп.1-5 или 6, дополнительно содержащий этап, на котором вычисляют целевую функцию, отображающую различие между измеренными промысловыми данными и прогнозными промысловыми данными. 8. Способ по пп.1-6 или 7, в котором этап, на котором вычисляют обновленный вектор состояния,включает в себя этап, на котором используют коэффициент демпфирования. 9. Способ по пп.1-5 или 6, дополнительно содержащий этапы, на которых вычисляют целевую функцию на основе измеренных промысловых данных и прогнозных промысловых данных и заменяют начальный вектор состояния на прогнозный согласованный вектор состояния и итерируют этапы (b)-(f), используя коэффициент демпфирования до тех пор, пока целевая функция не будет в рамках предопределенных критериев. 10. Способ по п.8 или 9, в котором коэффициент демпфирования вычисляется с использованием математического выражения где ik - коэффициент демпфирования в момент времени tk на итерации i со значением между 0 и 1;yu,i+1k,j - обновленный вектор состояния в момент времени tk на итерации i+1;yu,ik,j - обновленный вектор состояния в момент времени tk на итерации i;Gik - вычисленное приращение на этапе (с), причем приращением является приращение Калмана на итерации i;dik,j - измеренные промысловые данные в момент времени tk на итерации i;Hk - матричный оператор, который связывает прогнозный вектор состояния с вектором промысловых данных в начальном векторе состояния в момент времени tk; иyf,ik,j - прогнозный вектор состояния в момент времени tk на итерации i. 11. Способ по пп.1-9 или 10, в котором обновленная совокупность моделей коллектора дополнительно обновляется посредством выполнения этапов, на которых:(g) вычисляют второе приращение на основе новых измеренных промысловых данных и прогнозного согласованного вектора состояния;(h) вычисляют второй обновленный вектор состояния, используя второе приращение, причем второй обновленный вектор состояния включает в себя новые обновленные статические переменные состояния;(i) создают второй согласованный вектор состояния, включающий в себя новые обновленные статические переменные состояния и новые прогнозные динамические переменные состояния; и(j) прогнозируют вперед от второго временного шага к третьему временному шагу второй согласованный вектор состояния для вычисления второго прогнозного согласованного вектора состояния, который включает в себя вторые прогнозные статические и динамические переменные состояния, согласованные друг с другом; при этом совокупность моделей коллектора дополнительно обновляется на компьютере вторым прогнозным согласованным вектором состояния, который включает в себя вторые прогнозные статические и динамические переменные состояния, согласованные друг с другом. 12. Машиночитаемое устройство хранения программы, материально воплощающее программу выполнимых инструкций, которые, при выполнении посредством машины, осуществляют этапы способа обновления совокупности моделей коллектора, проведения моделирования коллектора, при этом упомянутые этапы способа характеризуются тем, что:(a) генерируют совокупность моделей коллектора, причем совокупность представляется на первом временном шаге посредством начального вектора состояния начальных статических и динамических переменных состояния;(b) от первого временного шага ко второму временному шагу прогнозируют вперед начальный век- 14013657 тор состояния для вычисления прогнозного вектора состояния, который включает в себя прогнозные статические и динамические переменные и прогнозные промысловые данные;(c) вычисляют приращение на основе прогнозного вектора состояния и измеренных промысловых данных;(d) вычисляют обновленный вектор состояния, включающий в себя обновленные статические переменные состояния с использованием вычисленного приращения по этапу (с);(e) создают согласованный вектор состояния, включающий в себя обновленные статические переменные состояния этапа (d) и начальные динамические переменные состояния этапа (а); и(f) от первого временного шага ко второму временному шагу прогнозируют вперед согласованный вектор состояния для вычисления прогнозного согласованного вектора состояния, который включает в себя новые прогнозные статические и динамические переменные состояния, согласованные друг с другом; при этом совокупность моделей коллектора обновляется прогнозным согласованным вектором состояния, который включает в себя новые прогнозные статические и динамические переменные состояния, согласованные друг с другом.