Формирование геологической модели
Формула / Реферат
1. Способ формирования геологической модели области среды, содержащий этапы, на которых:
i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;
ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;
iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;
iv) вычисляют неопределенности положений в трех измерениях по меньшей мере некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; и
v) формируют геологическую модель из положений в трех измерениях множества точек области, определенных на этапе (iii) с неопределенностями положений в трех измерениях, вычисленными на этапе (iv) .
2. Способ по п.1, в котором, по меньшей мере, некоторые из точек располагают на по меньшей мере одной границе раздела, идентифицированной по сейсмическим данным, между подобластями области различных скоростей сейсмических волн.
3. Способ по п.1, в котором, по меньшей мере, некоторые из точек располагают на разрывах, идентифицированных по сейсмическим данным.
4. Способ по п.1, в котором неопределенность времени пробега определяют по длине волны сейсмической волны, используемой для получения сейсмических данных.
5. Способ по п.1, в котором неопределенность скорости определяют на основании сведений о геологии области.
6. Способ по п.1, в котором на этапе (iii) определяют положение каждой из точек с помощью одной из функций: положения на вышележащей границе раздела, где луч, падающий на точку, пересекает вышележащую границу раздела; скорости сейсмической волны от положения до точки, полученной на основании скоростной модели; и времени пробега от положения до точки, полученной по сейсмическим данным.
7. Способ по п.6, в котором на этапе (iv) осуществляют дифференцирование функции.
8. Способ по п.7, в котором функция включает в себя первую подфункцию, представляющую закон Снелла, и вторую подфункцию, представляющую наклон при положении, и на этапе (iv) определяют производные первой и второй подфункций.
9. Способ по п.1, в котором этап (v) включает в себя приписывание корреляций среди, по меньшей мере, некоторых из точек.
10. Способ по п.1, в котором дополнительно приписывают корреляции среди значений скорости в скоростной модели.
11. Способ по п.1, в котором геологическая модель представляет собой первую геологическую модель, и способ дополнительно содержит этапы, на которых:
vi) подготавливают получаемые не сейсмическим способом трехмерные данные о положении и трехмерные данные о неопределенности положения вокруг области; и
vii) корректируют первую геологическую модель с помощью данных, подготовленных на этапе (vi), чтобы получить вторую геологическую модель.
12. Способ по п.11, в котором получаемые не сейсмическим способом данные содержат данные о маркерах скважины.
13. Способ по п.11, в котором на этапе (vii) осуществляют выбор по меньшей мере одной общей точки из области, которая является общей для первой геологической модели и для получаемых не сейсмическим способом данных, и определяют положение и неопределенность положения общей точки во второй геологической модели на основании положений и неопределенностей положений общей точки в первой геологической модели и в получаемых не сейсмическим способом данных.
14. Способ по п.13, в котором по меньшей мере одна общая точка представляет общие или граничащие геологические признаки.
15. Способ по п.14, в котором получаемые не сейсмическим способом данные содержат данные о маркерах скважины и по меньшей мере одна общая точка представляет место на одной границе раздела в первой геологической модели и место в получаемых не сейсмическим способом данных, где скважина проходит через границу раздела.
16. Способ по п.15, в котором на этапе (vii) перемещают место общей точки в первой геологической модели, по существу, параллельно пути луча или на соседнее место.
17. Способ по п.14, в котором по меньшей мере одна общая точка представляет место на разрыве в первой модели и место в получаемых не сейсмическим способом данных, где скважина проходит через разрыв.
18. Способ по п.17, в котором на этапе (vii) перемещают место общей точки в первой геологической модели, по существу, перпендикулярно к поверхности разрыва.
19. Способ по п.16, в котором дополнительно обновляют получаемые не сейсмическим способом данные путем перемещения места общей точки в получаемых не сейсмическим способом данных в направлении, по существу, противоположном направлению перемещения в первой геологической модели.
20. Способ по п.18, в котором дополнительно обновляют получаемые не сейсмическим способом данные путем перемещения места общей точки в получаемых не сейсмическим способом данных в направлении, по существу, противоположном направлению перемещения в первой геологической модели.
21. Способ по п.11, в котором на этапе (vi) обеспечивают получаемые не сейсмическим способом данные о скорости и данные о неопределенности скорости вокруг области.
22. Способ по п.21, в котором дополнительно образуют и/или обновляют скоростную модель в соответствии с получаемыми не сейсмическим способом данными о скорости и неопределенности скорости.
23. Способ по п.11, в котором этап (vii) выполняют при наличии ограничения, такого, что пересечения граница/разрыв сохраняются во второй геологической модели.
24. Способ по п.13, в котором на этапе (vii) осуществляют выбор множества общих точек и корректировку первой геологической модели за один этап.
25. Способ по п.18, в котором на этапе (vii) осуществляют корректировку первой геологической модели на первом этапе относительно по меньшей мере одной общей точки на границе и затем на втором этапе относительно по меньшей мере одной общей точки на разрыве.
26. Способ по п.11, в котором на этапе (vii) осуществляют корректировку первой геологической модели рекурсивно слой за слоем.
27. Компьютер, содержащий программу для выполнения способа образования геологической модели области среды, и этот способ содержит этапы, на которых:
i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;
ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;
iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;
iv) вычисляют неопределенности положений в трех измерениях, по меньшей мере, некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; и
v) формируют геологическую модель из положений в трех измерениях множества точек области, определенных на этапе (iii) с неопределенностями положений в трех измерениях, вычисленными на этапе (iv).
28. Считываемый компьютером носитель данных, содержащий программу, выполненную с возможностью программирования компьютера для выполнения способа образования геологической модели области среды, и этот способ содержит этапы, на которых:
i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;
ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;
iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;
iv) вычисляют неопределенности положений в трех измерениях, по меньшей мере, некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; и
v) формируют геологическую модель из положений в трех измерениях множества точек области, определенных на этапе (iii) с неопределенностями положений в трех измерениях, вычисленными на этапе (iv).
29. Способ бурения скважины в области геологической среды на основе геологической модели области среды, содержащий этапы, на которых:
i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;
ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;
iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;
iv) вычисляют неопределенности положений в трех измерениях, по меньшей мере, некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; и
v) формируют геологическую модель из положений в трех измерениях множества точек области, определенных на этапе (iii) с неопределенностями положений в трех измерениях, вычисленными на этапе (iv), и
управляют бурением в соответствии с геологической моделью.
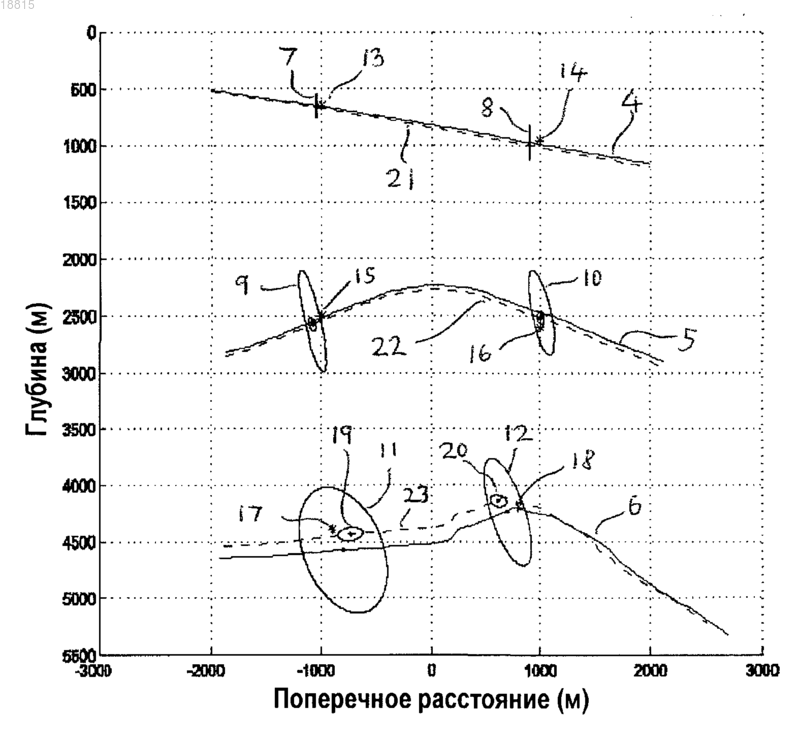
Текст
Предложен способ формирования геологической модели области среды. Сейсмические данные получают из области, и они включают в себя неопределенность времени пробега сейсмической волны. Кроме того, формируют сейсмическую скоростную модель области, и она включает в себя неопределенность скорости. Выполняют трассирование лучей по сейсмическим данным, для чего используют скоростную модель для определения положений в трех измерениях множества точек области. Неопределенности (7-12) положений в трех измерениях, по меньшей мере, некоторых из точек вычисляют на основании неопределенности времени пробега и неопределенности направления распространения луча. Их объединяют с положениями, определенными путем трассирования лучей, чтобы сформировать геологическую модель. Настоящее изобретение относится к способу формирования геологической модели. Предшествующий уровень техники Данные о временах пробега сейсмических волн и данные о маркерах скважины объединяют для каждого нефтяного коллектора, чтобы получать уточненные сведения относительно геологических запасов нефти, неоднородностей углеводородов, оценивать степень риска, а в общем случае принимать лучшие решения относительно стратегий бурения и дренажа. Сейсмические и скважинные данные сильно различаются, и способ объединения в значительной степени зависит от основной задачи исследования. Для получения наилучших данных необходимо учитывать неопределенность, связанную с данными каждого вида. Рассмотрим, например, толщину нефтяного коллектора. По показаниям одного источника (скважинного) данных она составляет 30 м, по показаниям второго (сейсмического), например, 50 м. Какую ценность представляет этот коллектор в показателях чистой приведенной стоимости Следует ли начинать добычу углеводородов Если критическая толщина, основанная на стоимости и ожидаемом объеме продаж, составляет 40 м, то для начала добычи придется меньше полагаться на первый источник, чем на второй. Сейсмические данные регистрируют, излучая звук от источника, такого как воздушная пушка, и затем контролируя отраженный сигнал на ряде приемников. Имеется очень много литературы по преобразованию таких данных способа отраженных волн в структурную модель геологической среды, представляемой в координатах с восточным, северным и глубинным положениями. Наиболее распространенный способ заключается в ручной обработке пропикированных времен вступления отраженных волн (времен пробега) от основных геологических границ путем сбора их относительно фиксированных опорных положений на поверхности и затем растяжения времен пробега (измеряемых в секундах) в соответствии с заранее известной скоростью. Одна оговорка, связанная с этим способом, заключается в отсутствии возможности получения в структурной модели неопределенности по трем измерениям. Другая заключается в неявном допущении, что каждая опорная точка поверхности представляет точку отражения, находящуюся ниже, а не точку другой отражающей границы к востоку или северу от местоположения поверхности. Второе предположение (имеющее отношение к "вертикальному растяжению", поскольку только глубинный размер является влияющим при структурном построении) можно обойти с помощью более сложных способов глубинного преобразования, например, используя трассирование лучей, но остается проблема получения структурной неопределенности в трех измерениях. Данные о маркерах скважины составляют из пропикированных географических положений (восток,север, глубина), по мере прохождения скважины через геологические маркирующие горизонты. Эти маркирующие горизонты обычно включают в себя границы, обнаруживаемые в сейсмических данных. Обычно скважинные данные обрабатывают как фиксированные, известные или, по меньшей мере, относительно фиксированные результаты измерений по сравнению с зашумленными сейсмическими данными. Однако с помощью современных компьютеров обработка сейсмических данных становится более достоверной, а отношение сигнала к шуму повышается. В то же самое время технология строительства скважин обуславливает значительный рост количества искривленных и глубоких (глубиной 5 км) скважин. В таком случае измеряемые положения скважин являются менее достоверными. Это означает, что данные о маркерах скважины нельзя трактовать как фиксированные, известные географические положения, легко используемые для пересчета сейсмических данных из временной в глубинную область. В настоящее время неопределенности положений маркеров скважины, регистрируемых в процессе бурения,изменяются в соответствии с используемым оборудованием. Это повышает неопределенность анализа во время бурильных работ. Основное ограничение современной технологии заключается в том, что положение маркера скважины и неточность положения включаются в основную картину определения местоположения в пространстве. Это влечет за собой объединение географических опорных границ раздела в координатах с восточным, северным и глубинным положениями. Скважины являются разреженными(10-50 скважин на нефтяном месторождении) и несут немного информации о поперечной непрерывности коллектора. С другой стороны, сейсмические данные являются избыточными и информативными о поперечном направлении, но не являются непосредственно сравнимыми при использовании шкалы восточных, северных, глубинных положений маркера скважины. Известны оптимальные способы объединения разнообразных данных на общей шкале. В учебниках по статистике их называют общим термином "оценивание методом наименьших квадратов". Средства для представления сейсмических данных в координатах с восточным, северным и глубинным положениями и объединение этих данных с географическими данными о маркерах скважины отсутствуют, особенно на уровне, когда можно получать неопределенность положения в пространстве. Традиционным путем является обновление в вертикальном направлении. Для почти плоских горизонтов это приводит к достоверному способу, но в случае наклонных слоев, криволинейных поверхностей или разрывов это может вносить систематическую ошибку. Предлагались способы ортогонального сдвига наклонных поверхностей, но они все же относятся к специальным способам, которыми не получают внутренней изменчивости направления, которую на самом деле можно физически моделировать, используя, например,трассирование лучей. Кроме того, состоятельное оценивание неопределенностей является значимым,чтобы быстро принимать решения для системы коллекторов высокой размерности. Текущее состояние области техники, к которой относится изобретение, характеризуется поиском "наилучшей" структурной модели без управления данными, передаваемыми на оценивание. Поэтому обновление географической модели в соответствии с существующими стандартами является трудоемким процессом, при этом должна выполняться очень большая работа, связанная с повторной итерацией данных и попыткой согласования информации, которая не может быть унифицирована. В патентом документе ЕР 1306694 раскрыт способ объединения первой и второй моделей общей области пространства, такой как область геологической среды ниже поверхности, для образования третьей модели. Общие точки имеют различные положения в первой и второй моделях. Заданная корреляция существует между положениями общих точек в первой модели и положениями точек, представляющих интерес, в первой модели. Положения общих точек в третьей модели получают на основании положений общих точек в первой и второй моделях. Положения точек, представляющих интерес, в третьей модели получают на основании положений общих точек в третьей модели и на основании заданной корреляции. В патентном документе GB 235274 6A раскрыт способ получения вероятностных диаграмм положений точек падения для скважины. Фиксированную заданную точку находят на исходном месте на поверхности с помощью сетки, состоящей из узлов и ячеек сетки. Вектор неопределенности приписывают к каждому узлу и определяют, применяя статистический метод Монте-Карло. Когда значения для всех узлов вычислены, находят результирующее распространение местоположения. Заданную точку проецируют на каждое распространение местоположения с тем, чтобы определить точку падения. Распределение набора входных точек переносят на поверхность, и плотность точек падения дает вероятность существования любой точки поверхности как точки падения. Плотность вероятности отображают в виде линий уровня. В патентном документе GB 2325523A раскрыт способ формирования карт рисков при определении местоположения скважины в среде. В способе используют первый интерпретированный горизонт, извлеченный из массива мигрированных сейсмических данных, при этом, по меньшей мере, первое значение скорости включает в себя неопределенность скорости. Второй интерпретированный горизонт образуют миграцией первого горизонта, используя второе значение скорости, равное первому значению с добавлением неопределенности. Третий интерполированный горизонт образуют миграцией первого горизонта,используя третье значение скорости, равное первому значению за вычетом неопределенности. Точку положения для скважины выбирают на первом горизонте и наносят на карту вертикаль, которая проходит через точку и пересекает второй и третий горизонты в мигрированных точках. На втором интерпретированном горизонте определяют положения, соответствующие мигрированным точкам, при этом первый участок интерпретированного горизонта, расположенный между указанными положениями, образует геометрическое место потенциальных положений скважины с учетом неопределенности. В Международной заявке WO 97/38330 раскрыт способ трехмерного геологического моделирования. В заявке 2004/0220789 А 1 на патент США раскрыт способ вычисления реализации коллектора углеводородов на сетке. Краткое изложение существа изобретения В соответствии с первым объектом изобретения предложен способ формирования геологической модели области среды, содержащий этапы, на которых:i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;iv) вычисляют неопределенности положений в трех измерениях, по меньшей мере, некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; иv) объединяют положения, определенные на этапе (iii), с неопределенностями, вычисленными на этапе (iv), чтобы образовать первую геологическую модель. По меньшей мере, некоторые из точек могут быть расположены на по меньшей мере одной границе раздела, идентифицированной по сейсмическим данным, между подобластями области различных скоростей сейсмических волн. По меньшей мере, некоторые из точек могут быть расположены на разрывах, идентифицированных по сейсмическим данным. Неопределенность времени пробега может быть определена по длине волны сейсмической волны,используемой для получения сейсмических данных. Неопределенность скорости может быть определена на основании сведений о геологии области. Этап (iii) может содержать определение положения каждой из точек как функции: положения на вышележащей границе раздела, где луч, падающий на точку, пересекает вышележащую границу раздела; скорости сейсмической волны от положения до точки, полученной на основании скоростной модели; и времени пробега от положения до точки, полученной по сейсмическим данным. Этап (iv) может содержать дифференцирование функции. Функция может включать в себя первую подфункцию, представляющую закон Снелла, и вторую подфункцию, представляющую наклон при положении, а этап (iv) может содержать определение производных первой и второй подфункций. Этап (v) может включать в себя приписывание корреляций среди, по меньшей мере, некоторых из точек. Способ может дополнительно содержать приписывание корреляций среди значений скорости в скоростной модели. Способ может содержать дополнительные этапы, на которых:vi) обеспечивают получаемые не сейсмическим способом трехмерные данные о положении и трехмерные данные о неопределенности положения вокруг области; иvii) корректируют первую геологическую модель с помощью данных, подготовленных на этапе (vi),чтобы получить вторую геологическую модель. Получаемые не сейсмическим способом данные могут содержать данные о маркерах скважины. Этап (vii) может содержать выбор по меньшей мере одной общей точки из области, которая является общей для первой геологической модели и для получаемых не сейсмическим способом данных, и определение положения и неопределенности положения общей точки во второй геологической модели на основании положений и неопределенностей положений общей точки в первой геологической модели и в получаемых не сейсмическим способом данных. По меньшей мере одна общая точка может представлять общие или граничащие геологические признаки. По меньшей мере одна общая точка может представлять место на одной границе раздела в первой геологической модели и место в получаемых не сейсмическим способом данных, где скважина проходит через границу раздела. Этап (vii) может содержать перемещение места общей точки в первой геологической модели, по существу, параллельно пути луча или на соседнее место. По меньшей мере одна общая точка может представлять место на разрыве в первой модели и место в получаемых не сейсмическим способом данных, где скважина проходит через разрыв. Этап (vii) может содержать перемещение места общей точки в первой геологической модели, по существу, перпендикулярно к поверхности разрыва. Способ может дополнительно содержать обновление получаемых не сейсмическим способом данных путем перемещения места общей точки в получаемых не сейсмическим способом данных в направлении, по существу, противоположном направлению перемещения в первой геологической модели. Этап (vi) может содержать подготовку получаемых не сейсмическим способом данных о скорости и данных о неопределенности скорости вокруг области. Способ может дополнительно содержать формирование и/или обновление скоростной модели в соответствии с получаемыми не сейсмическим способом данными о скорости и неопределенности скорости. Этап (vii) может выполняться при наличии ограничения, такого, что пересечения граница/разрыв сохраняются во второй геологической модели. Этап (vii) может содержать выбор множества общих точек и корректировку первой геологической модели за один этап. Этап (vii) может содержать корректировку первой геологической модели на первом этапе относительно по меньшей мере одной общей точки на границе и затем на втором этапе относительно по меньшей мере одной общей точки на разрыве. Этап (vii) может содержать корректировку первой геологической модели рекурсивно слой за слоем. В соответствии со вторым объектом изобретения предложена компьютерная программа, выполненная с возможностью программирования компьютера для выполнения способа согласно первому объекту изобретения. В соответствии с третьим объектом изобретения предложен компьютер, содержащий программу или программируемый программой согласно второму объекту изобретения. В соответствии с четвертым объектом изобретения предложен считываемый компьютером носитель данных, содержащий программу согласно второму объекту изобретения. В соответствии с пятым объектом изобретения предложена передача программы согласно второму объекту изобретения. В соответствии с шестым объектом изобретения предложен способ бурения скважины в области геологической среды, содержащий выполнение способа согласно первому объекту изобретения и управление бурением в соответствии с геологической моделью. Согласно изобретению можно получить способ, которым обеспечивается информация высокого качества о геологии области среды. Его можно использовать, например, для принятия лучших решений относительно стратегий бурения и дренажа. Краткое описание чертежей В дальнейшем изобретение будет описано для примера с обращением к сопровождающим чертежам, на которых: фиг. 1 - график зависимости времен пробега сейсмических волн в миллисекундах от поперечного расстояния в метрах, иллюстрирующий три подземных горизонта, выбранных на основании данных о временах пробега сейсмических волн; фиг. 2 - график зависимости глубины в метрах от поперечного расстояния в метрах, иллюстрирующий результат трассирования лучей по данным, показанным на фиг. 1; фиг. 3 - график зависимости глубины в метрах от поперечного расстояния в метрах с показом границ между слоями, полученных по данным, показанным на фиг. 2, и эллипсоидов 95-процентной неопределенности; фиг. 4 - график, аналогичный представленному на фиг. 3, с показом границ и эллипсоидов из фиг. 3 и границ и эллипсоидов после обработки способом, составляющим осуществление изобретения; фиг. 5 - схематическая иллюстрация выбора пар общих точек на горизонте; фиг. 6 - схематическая иллюстрация обновления геологической модели с использованием ограничения в направлении падающего луча относительно пары общих точек; фиг. 7 - схематическая иллюстрация выбора пар общих точек на разрыве; фиг. 8 - схематическая иллюстрация обновления геологической модели с использованием ограничения вдоль нормали к поверхности относительно пары общих точек; фиг. 9 а-9 с - схемы, иллюстрирующие скоростные модели сейсмических волн различных видов; и фиг. 10 - схема, иллюстрирующая ограничение скоростной модели и вследствие этого геологической модели на основании результатов скважинных измерений скорости. Описание предпочтительных вариантов воплощения изобретения В способе, составляющем осуществление изобретения, необходимыми входными данными являются:i) Данные о временах пробега сейсмических волн для горизонтов и разрывов, представляющих интерес. Их получают в виде некоторого количества местоположений точек на горизонтальной сетке с направлением координат на север, восток. Предполагается, что эти данные обрабатывают так, что они представляют время пробега используемой сейсмической волны, излучаемой из точки поверхности и отражаемой от горизонта, представляющего интерес. Такая обработка является первым этапом любого алгоритма интерпретации сейсмических данных. Неопределенность, связанная с пикингом времени пробега, может быть параметром по умолчанию,обычно связанным с длиной волны сейсмического сигнала, например, стандартным отклонением, составляющим 10 мс. Для разрывов неопределенность ручного пикинга значительно больше, поскольку сигнал слабее, и поэтому требуются дополнительные геологические интерпретации.ii) Значения скорости для каждого интервала в среде. Их берут из априорной геологической информации. Кроме того, стандартное отклонение значений интервальной скорости можно получать из априорного представления о неопределенности или однородности в географической зоне, представляющей интерес. Неопределенность скорости обычно возрастает на более глубоких интервалах. Например, скорость в морской воде составляет 1500 м/с при стандартном отклонении около 1 м/с. В глубоких слоях скорость может быть 3000 м/с при стандартном отклонении около 100 м/с.iii) Данные о маркерах скважины для всех скважин, проходящих через основные горизонты, интерпретируемые на основании данных о временах пробега сейсмических волн. Неопределенность маркеров скважины обычно является неотъемлемым атрибутом в алгоритмах регистрации данных. В случае вертикальных скважин неопределенности в восточном, северном направлениях являются небольшими; в случае искривленных скважин неопределенности в восточном, северном направлениях являются более значительными. Неопределенность также зависит от каротажного оборудования, используемого в скважине. Обычные способы определения расположения скважин включают в себя использование магнитных приборов, гироскопов и гравитационных индикаторов. Выходными данными для такого способа являются:i) Структурная модель для географических положений в трех измерениях: восток, север и глубина. Эти выходные данные о положении в трех измерениях представляют собой оптимальную оценку, основанную на входных данных и наборе фиксированных параметров из априорных сведений.ii) Структурная неопределенность и корреляция для всех положений в трех измерениях: восток, север и глубина. Эти выходные данные представляют собой стандартное отклонение трех координат всех положений и корреляции между ними. Некоторые местоположения могут иметь более высокую неопределенность по направлению глубины, тогда как другие могут иметь наибольшую неопределенность в северо-восточном направлении. Отметим, что также имеется корреляция между двумя различными точками, показывающая, что произойдет с точкой В, если точка А сдвинется в одном направлении.iii) Скоростная модель, ограниченная сейсмическими данными и информацией о маркерах скважины, и корреляция между интервальной скоростью и всеми географическими точками в структурной модели. Она показывает, что произойдет с точками, если интервальная скорость изменится.iv) Унифицированная модель с учетом ограничений, включенных в обновление. Менее необходима при ручной обработке. На основании выходных данных может быть принят ряд важных решений относительно, например,оптимального размещения скважин, расстояния до объекта разведки, прогнозирования зон высокого дав-4 018815 ления впереди ствола скважины, вычисления чистой приведенной стоимости нефти или газа в зоне коллектора в процессе бурения, обновления модели при совместном выполнении операций и обновления скорости в случае итерационной обработки сейсмических данных. Приведенным ниже примером иллюстрируется способ для относительно простого случая с тремя границами горизонтов, тремя значениями интервальных скоростей и двумя маркерами скважины на каждой границе. Первый этап в способе заключается в преобразовании результатов сейсмических временных измерений в координаты с направлением осей на восток, север и в глубину вместе с соответствующими неопределенностями и корреляциями. Это делают трассированием воображаемых лучей, используя идею, в соответствии с которой географическую точку отражения из сейсмических данных после временной миграции помещают при трассировании луча непосредственно ниже поверхности. Когда этот луч попадает на границу раздела, он изгибается в соответствии с относительным изменением скорости на двух слоях. В таком случае угол передачи можно вычислить на основании закона Снелла. В пределах каждого слоя луч трассируют в течение времени, указываемого данными о времени пробега сейсмической волны. В общей сложности это дает одну точку отражения на каждой границе раздела для каждой опорной точки поверхности. Основными этапами преобразования в координаты с направлением осей в глубину, на восток, север являются следующие. Начинают с координат поверхности и постепенно опускаются в глубину на расстояние, указанное скоростью в верхнем интервале и временем, до первой границы 1, показанной на фиг. 1. На первой границе имеется некоторое количество точек отражения. Локальный наклон первого горизонта можно вычислить, используя локальные окрестности точек. Этот наклон и нисходящий луч создают угол падения, а из закона Снелла следует, что синус угла передачи дается относительной разностью скоростей в двух слоях, умноженной на синус угла падения. Этот закон используют для трассировки луча от первой границы 1 до второй границы 2, и на этом интервале времени используют скорость во втором слое и время, указанные данными о временах пробега сейсмической волны для этого слоя. Как показано на фиг. 2, теперь луч больше не является вертикальным, за исключением случаев, когда скорости в двух слоях равны или угол наклона первой поверхности равен нулю. Процесс применения закона Снелла на границе продолжают для второго слоя и используют для географических точек в самом нижнем третьем слое. На фиг. 1 показаны пропикированные данные о временах пробега сейсмических волн для трех горизонтов. По вертикальной оси отложено время (в миллисекундах). На фиг. 2 показаны лучи, идущие вниз от поверхности и искривляющиеся на границах раздела. Полученные в результате глубинного преобразования горизонты 4, 5 и 6 до некоторой степени отличаются от горизонтов 1, 2 и 3,полученных в результате вертикального растяжения. Это указывает на систематическую ошибку, вносимую в предположении отсутствия искривления на границах раздела. Также отметим, что лучи искривляются больше, если локальный наклон больше. Это вытекает из закона Снелла. При преобразовании по глубине, восточному направлению, северному направлению, описанному выше, каждую глубинную точку вычисляют как функцию скоростей, данных о временах пробега и по точкам отражения на границах раздела в вышележащих слоях. Связанную с этим неопределенность вычисляют, дифференцируя эту функциональную зависимость, то есть используя линеаризацию нелинейных функциональных зависимостей. Распространение ошибки, основанное на линеаризованном операторе, используют для распространения неопределенности из функциональной входной переменной в выходную переменную. Беря производные всех функциональных зависимостей, включенных в закон Снелла, и вычисляя угол падения, таким путем также можно вычислить стандартное отклонение всех точек по глубине, корреляцию между всеми точками и корреляцию между параметрами интервальной скорости и всеми точками. На практике это означает, что при все более и более глубоком трассировании лучей осуществляют вычисление не только точек отражения, но в дополнение к этому производных всех результатов вычислений. В таком случае выходными данными в результате преобразования времен пробега сейсмических волн являются i) ожидаемые точки отражения в координатах с направлением осей по глубине, на восток и север и ii) неопределенность и корреляции между всеми этими точками отражения и скоростями. На фиг. 3 показана неопределенность двух местоположений в каждом слое в направлении глубины,востока и севера. Эти эллипсоиды с 7 по 12 неопределенности получены по данным о временах пробега без использования на этом этапе скважинной информации. Эти эллипсоиды представляют собой 95 процентные области, показывающие, что имеется 95-процентная вероятность того, что истинная точка отражения находится в пределах этого эллипса. Отметим, что неопределенность агрегируется по мере продвижения на большую глубину и поэтому эллипсы становятся больше при самой глубокой границе раздела. Когда лучи проходят через область с большим наклоном, для нижележащей границы получается более высокая горизонтальная (восточная, северная) неопределенность. Это является естественным, поскольку неопределенность сильно связана с синусом угла передачи через закон Снелла. Наконец, маркеры скважины используют вместе со связанной с ними неопределенностью. Теперь до обновления структурной модели по сейсмическим данным введем концепцию "общих точек": они представляют собой географические координаты, которые являются общими для скважинных измерений и сейсмических координат с направлением осей в глубину, на восток и север. Поскольку ни данные о маркерах скважины, ни точки, получаемые по сейсмическим данным, не свободны от шума, общие точки являются неизвестными. Тем не менее, известно, что маркер скважины и сейсмические географические координаты представляют один и тот же геологический признак; поэтому можно подобрать сейсмическую общую точку для маркера скважины. Зададим ограничения для этих общих точек. Ограничения являются информативными относительно направления, в котором следует обновлять сейсмические координаты с направлением осей в глубину, на восток и север. Ограничения лежат в основе способа объединения в модели общих точек и всех других точек. В то время как количество точек может быть несколько тысяч, количество общих точек обычно меньше (около 100 маркеров скважины). Оптимальную оценку географических положений вычисляют как стандартное решение методом наименьших квадратов, но дополнительная степень гибкости придается представлением общих точек и трехмерным обновлением. В частности, обновление точек вдоль исходной траектории луча представляется интересным. Неопределенность всех точек обновляют в рамках методики наименьших квадратов. Они являются наименее близкими к общим точкам, поскольку при этом имеются два источника информации. Они находятся дальше всего от общих точек и на больших глубинах. На фиг. 4 данные о маркерах скважины показаны позициями с 13 по 18. Общие точки обновлены и интегральная оценка обозначена наряду с эллипсоидами неопределенности, такими как 19 и 20 на фиг. 4. Заметно, что обновленные эллипсоиды (19, 20) неопределенности меньше, чем эллипсоиды (11, 12) неопределенности, полученные только по сейсмическим данным, поскольку неопределенность отбивок скважины до некоторой степени меньше в этом случае. Пунктирными линиями на фиг. 4 представлены обновленные горизонты 21, 22 и 23, полученные по сейсмическим данным и отбивкам скважины. Они несколько сдвинуты от горизонтов 4, 5 и 6, соответственно, оцененных с использованием только сейсмических данных, но большей частью локально благодаря интервалу корреляции в статистической модели. Ниже предполагается, что выполняется трассирование воображаемых лучей, так что все данные о разрывах и горизонтах преобразуются в координаты с направлением осей на север, восток и в глубину. Кроме того, представлена скоростная модель, используемая при трассировании воображаемых лучей. Представлена ковариационная матрица, описывающая неопределенность и корреляции (зависимость) всех данных (скоростей, пространственных сейсмических положений и маркеров скважины). Для обновления этой модели с использованием маркеров скважины используют статистическое вычисление, основанное на математике наименьших квадратов. Ниже описаны ограничения различных видов. Могут использоваться сочетания ограничений любых видов и нескольких маркеров скважины. Статистическое обновление можно выполнять тремя способами.i) Обновление с использованием сразу всех маркеров скважины, при этом выбирают все общие точки (описанные далее) из исходного набора данных о трассированных лучах.ii) Двухэтапное обновление. Сначала корректируют модель, используя скорость и маркеры скважины из горизонтов. Затем вычисляют общие точки разрывов в скорректированной модели и используют их для обновления скорректированной за влияние скважины и горизонтов модели, используя маркеры скважины из разрывов.iii) Последовательное обновление. В этом варианте модель сначала корректируют с помощью маркеров скважины, принадлежащих к самому верхнему горизонту и самому верхнему скоростному слою. После этого получившуюся модель используют, чтобы вычислить общие точки маркеров скважины для скоростей и горизонтов, принадлежащих к следующему слою, и корректируют, используя маркеры скважины, принадлежащие ко второму слою. Этот процесс продолжают до тех пор, пока все скорости и горизонты не будут пройдены. Модель, получившуюся в результате этого процесса, используют для вычисления общих точек маркеров скважины, связанных с разрывами, и дополнительно корректируют, используя наложенные на разрывы ограничения. Независимо от того, какую из этих стратегий выбирают, неопределенность обрабатывают когерентным способом путем корректировки, что приводит в результате к обновленным неопределенностям для всех входных данных, которые получают на основании всех входных неопределенностей и корреляций. Поскольку маркер скважины из горизонта представляет только единственное положение точки, то точно неизвестно, какая точка сейсмического горизонта соответствует ему. В предположении, что разность между двумя общими точками в основном обусловлена неточностью интервальных скоростей, используемых при исходном трассировании лучей, точку горизонта, из которой продолжающийся падающий луч проходит ближе всего к маркеру скважины, выбирают соответствующей сейсмической общей точке для каждого маркера скважины. Эти два положения, выбранные таким образом, представляют пару общих точек, показанных позициями 24 и 25 на фиг. 5. Чтобы обновить сейсмическую модель, используя пару 24, 25 общих точек, задают ограничение между двумя точками. Как установлено ранее, точно не известно, какая точка сейсмического горизонта находится в соответствии с маркером скважины, за исключением того, что неточность скорости на всем протяжении падающего луча является наиболее вероятной причиной отсутствия пересечения маркера скважины и горизонта. Вследствие этого ограничение между двумя идентифицированными общими точками задают только в направлении трассирования падающего луча 26 выбранной общей точки 25 горизонта. Поэтому обновлением на основании единственной пары 24, 25 общих точек сейсмическая модель корректируется только в направлении луча, падающего на сейсмическую общую точку. Это показано на фиг. 6. Обновленные ограничения, полученные с использованием точек разрыва из пар общих точек, несколько отличаются от ограничений, полученных с использованием точек горизонта. Это в основном обусловлено тем, как разрыв, такой как 30 на фиг. 7, представлен в сейсмических данных. В исходных сейсмических данных точное местоположение разрыва не показано; только размытая область в сейсмических данных свидетельствует о наличии разрыва где-то внутри этой области. В таком случае интерпретатор сейсмических данных наилучшим образом интерпретирует разрыв в этой области на основе интуиции и предшествующих знаний и опыта. По этой причине, как показано на фиг. 7, точку 31 разрыва,через которую проходит соответствующая нормаль 32 к поверхности разрыва, лежащую ближе всего к соответствующему маркеру 33 скважины, выбирают в качестве сейсмической точки из пары общих точек. Как показано на фиг. 8, ограничение между двумя общими точками 31, 33 влияет на сейсмическую модель только в направлении нормали 32 к поверхности разрыва, проходящей через сейсмическую общую точку 31. Скорректированное положение разрыва показано позицией 34, а скорректированные положения общих точек позициями 35 и 36. Однако другими парами общих точек можно корректировать модель в других направлениях. При трассировании воображаемых лучей используют интервальные скорости для преобразования сейсмических данных в трехмерные данные о положении в координатах с направлением осей на север,восток и по глубине. При этом полную скоростную модель делят на секции, в которых соседние горизонты являются границами для каждого интервала. В пределах каждого такого интервала скорость в коренной породе моделируют различными способами. Например, как показано на фиг. 9 а, единственная скорость, такая как V1 и V2, может быть назначена для каждого интервала, такого как 40 и 41, и предполагается, что эта скорость применяется для всех точек в пределах интервала. Как показано на фиг. 9b, в качестве варианта соответствующая скорость Vij может быть приписана каждой j-ой трассе при трассировании лучей в пределах каждого интервала. В другом варианте набор скоростей Vij может быть приписан к j-тым положениям или точкам на iтых интервалах. В таком случае скорость в любой произвольной точке можно найти по интерполяционной функции. Например, скорость V1X в точке 42 дается интерполяционной функцией, показанной какF(V11,V12,V13,V14) на фиг. 9 с. Интерполяционная функция может, например, формировать взвешенное среднее скоростей в наборе положений в окрестности точки. Кроме того, результаты измерения скорости в коренной породе можно получать из скважин, пробуриваемых через моделируемую область. Чтобы каждый такой выбираемый результат измерения скорости был частью скорректированной модели, задают ограничивающее условие между скважинным измерением и соответствующей скоростью из исходной сейсмической скоростной модели. В случае, когда интервальную скорость моделируют как набор пространственно фиксированных скоростей, объединенных интерполяционной функцией, выбираемая скорость сейсмической волны является скоростью, моделируемой с помощью интерполяционной функции в точке, выбираемой из условия согласования с результатом скважинного измерения скорости. Как показано на фиг. 10, скорости V1, V2, V3, измеряемые во время бурения через область, можно использовать при трассировании лучей или можно использовать впоследствии для обновления сейсмической модели путем "коррекции" трассирования лучей. Обновленные горизонты показаны позициями с 44 по 46. В случае примера, показанного на фиг. 9 а, скорость в каждом интервале может быть сделана равной измеряемому значению или среднему из измеряемых значений в интервале. В случае примеров,показанных на фиг. 9b и 9 с, обратную интерполяционную функцию нескольких видов можно использовать для обновления значений модели на основании измеряемых значений. Чтобы гарантировать сохранение точек пересечения между горизонтами и разрывами после корректировки, можно добавлять ограничивающие условия на точки пересечения горизонтов и разрывов, при этом обеспечивается нахождение каждой выбираемой пары точек горизонт/разрыв на пересечении после корректировки. Дополнительная информация о предпосылках создания и осуществлениях изобретения дается в нижеследующих материалах. Введение Достоверное прогнозирование подземных разрывов и горизонтов является очень важным для нефтяной отрасли. Наилучшие оценки и неопределенность положений имеют большое значение в нескольких процессах принятия решения. Одним таким процессом является проектирование скважины, когда от этой информации зависят форма траекторий ствола скважины и также форма и положение объектов бурения (Haarstad et al., 2002; Prange et al., 2004). Неопределенность положения структур является принципиальной информацией при планировании регистрации новых данных о геологическом разрезе, предназначенных для лучшего понимания среды, и в процессе планирования стратегии дренажа коллектора. Оценки положений горизонта и разрыва, а также их неопределенности являются значимыми входными данными для прогнозирования оценок объемов добычи на месте залегания. В настоящее время большинство способов калибровки скважин основаны на изменении сейсмической скоростной модели до тех пор, пока она не будет в наибольшей степени соответствовать набору измеряемых в скважине скоростей. Это представляет собой продолжительный процесс со значительным взаимодействием с человеком. Затем несоответствие между пересчитанной в глубины моделью и маркерами скважины корректируют, используя методы кригинга, которыми корректируют пересчитанные в глубины горизонты до соответствия скважинам только в вертикальном направлении. Аналогично неопределенность положения вычисляют только в вертикальном направлении (Abrahamsen, 1992; Abrahamsenand Benth, 2001) . В некоторых случаях определение поперечного положения структур и после этого неопределенности является важным для принятия решений, особенно при проектировании скважины. Примерами таких структур являются области вблизи эрозионных поверхностей и в этих поверхностях, области вблизи разрывов и также области, в которых угол наклона горизонтов изменяется. Holden и соавторы в 2003 г. распространили стандартные модели на обработку горизонтов, чтобы они также включали в себя разрывные объекты, но разрывы моделировали, используя объекты, подвижные только в одном направлении. При геомоделировании, см., например, Caumon et al., 2004, общепринято представлять границы зон и обновлять их, поскольку большее количество данных становится доступным. Один такой способ, основанный на триангулированных поверхностях, был представлен Thore et al., 2002, и в нем рассмотрено несколько аспектов многофункционального интегрирования и квантификации неопределенности. В этих заявочных материалах представлен новый способ прогнозирования положений подземных горизонтов и разрывов с включением неопределенностей поперечных и глубинных положений, наряду с применениями его для проектирования скважины и обновления структурной модели. В этом способе объединяют данные о временах пробега сейсмических волн и маркеры положения скважины и преобразуют их в прогнозируемые поперечные и глубинные положения вместе с соответствующими неопределенностями и пространственными корреляциями. Объединение различных данных приводит к желаемым свойствам:i) Основные поперечные структуры сохраняются в прогнозах глубины вследствие большой поперечной непрерывности в интерпретируемых сейсмических данных.ii) Значимые коррекции неопределенности глубины и мелкомасштабные флуктуации включены через посредство отбивок скважины. Поскольку сейсмические данные и скважинные данные измеряют при наличии шума, статистическое объединение данных обоих видов обеспечивает прогнозирование, в котором получают уровень неопределенности глубинных и поперечных положений. Способ, используемый в этих заявочных материалах, кратко описывается следующим образом. Интерпретируемые данные о временах пробега сейсмических волн преобразуют в глубинные и поперечные положения, используя трассирование лучей (см., например, Hubral, 1977). Разрывы и горизонты обрабатывают в трех измерениях как точечные объекты, но неопределенность объектов разрывов может отличаться от неопределенности объектов горизонтов вследствие интерпретационных проблем при обработке сейсмических данных. Маркерами скважины корректируют исходную сейсмическую глубинную модель,используя результаты измерений положения ствола скважины вместе с набором ограничивающих условий для геологических границ. Для положений в трех измерениях используют гауссову модель, а коррекции выполняют на основе полученных моделированием ковариационных матриц (см., например,Cressie, 1993) . Схема этого документа имеет следующий вид. В разделе 2 вводится концепция трассирования сейсмических лучей для временной области с преобразованием в глубинную область, тогда как вычисление неопределенности, связанной с этим способом, представлено в разделе 3. В разделе 4 описывается предлагаемая модель с включением точек разрыва. Раздел 5 посвящен обновлению модели геологической среды по скважинным данным. Рассматриваются несколько вариантов объединения данных о маркерах скважин. Численные примеры методики представлены в разделе 6. Математические подробности вынесены в приложения. Миграция воображаемых сейсмических лучей Простейший способ преобразования пропикированных времен пробега сейсмических волн в глубинные и поперечные положения заключается в глубинном преобразовании с растяжением по вертикали. В этом случае предполагается, что при миграции во временной области позиционируются все отражатели в их точном поперечном положении, а пропикированные времена пробега просто растягиваются в вертикальном направлении с использованием интервальных скоростей. Более реалистичный способ, который рассматривается в этой заявке, заключается в глубинном преобразовании пропикированных времен пробега сейсмических волн с использованием трассирования воображаемых лучей (картографической миграции). Затем луч трассируют вниз в течение времени, указываемого мигрированными во временной области данными на этом конкретном поперечном месте. Этот воображаемый луч начинается на поверхности, проходит вдоль вертикальной оси и искривляется на границах геологических сред в соответствии с законом Снелла. Если миграция во временной области делается корректно, результаты после трассирования воображаемых лучей будут совпадать с результатами более сложной глубинной миграции. Аспекты глубинного преобразования сейсмических данных подробно рассмотрены в геофизическойal., 2004). Выбор способа зависит от геологической сложности среды. Методика, описанная в этом документе, предназначена для геологических условий умеренной сложности. Это означает, что простейшее вертикальное растяжение может быть причиной систематической ошибки, но предположительно трассирование лучей является достаточно реалистичным. Предположим, что имеются пропикированные двойные времена пробега сейсмических волн, обозначенные tk,l, k=1, K, nh, l=1, K, m, где m является количеством пропикированных отражающих границ, аnh количеством пропикированных времен пробега на каждом горизонте. Случай с различным количеством пропикированных значений в разных слоях является возможным, но для него требуются некоторые технические подробности. К этой теме вернемся в главе 0. Фиксированные положения (Nk,0, Ek,0, Dk,0) на поверхности, k=1, K, nh, задают как положения общей глубинной точки (в продольном направлении/поперечном направлении), используемые при временной обработке сейсмических данных. (Типичным случаем является Dk,0=0) . Интервальными скоростями являются v1, K, vm. Положения (Nk,l, Ek,l, Dk,l) являются геометрическими точками отражения для соответствующих пропикированных значений tk,1 времен пробега. Для самой верхней геологической границы лучи являются вертикальными и положения отражений выражаются как которые можно записать в краткой форме в виде где при этом сохраняются положения на поверхности в продольном и поперечном направлениях и фиксированные времена пробега сейсмических волн. Совместное расположение всех точек на верхнем горизонте дает вектор: В случае более глубоких слоев l=2, K, m и положения отражений вычисляют, используя закон Снелла на границах. Если угол падения относительно границы раздела составляет i, a скорости в верхнем и нижнем слоях даются vl и vl+1, соответственно, то угол передачи относительно этой границы составляет В таком случае точки отражений в нижнем слое можно вычислить с помощью нелинейной функции скоростей и точек в указанных выше слоях (дающих угол падения). Геометрические положения в этом способе вычисляют рекурсивно, продвигаясь глубже на каждом этапе. В краткой форме математическая зависимость может быть записана в виде: Подробности этой формулировки трассирования лучей вынесены в приложение. Для понимания этого способа важно отметить, что представляющие интерес переменные включают в себя: 1) Скорости в слоях: V=(v1, K, vm),2) Положения (северное, восточное и глубинное) для всех горизонтов: Н= (h1, K, hm) . Ниже эти переменные двух видов будут использоваться для обновления скважинных данных. Распространение сейсмической неопределенности В этом разделе описывается способ, используемый для вычисления неопределенности пересчитанных в глубины поперечных положений и глубинных положений. Вычисление представляет собой элементарное упражнение по вычислению среднего и ковариации в соответствии с линеаризованной моделью. Предположим, что в общем случае y=f(x) для некоторой функции f. В нашем случае в соответствии с этой функцией f осуществляют последовательное трассирование лучей, определяемое уравнением(2). Предположим также, чтоявляется ковариационной матрицей х. Ковариационная матрица у, , может быть аппроксимирована разложением Тейлора и равна где оценивают при среднем значении х. Следуя этой схеме, выражения в уравнениях (1) и (2) можно продифференцировать, чтобы привести В данном случае многие элементы будут равны нулю, поскольку прогнозируемые геометрические положения зависят только от малого числа переменных. Все столбцы из уравнения (3) собирают в матрицу, обозначаемую F1. Отметим, что при прогнозировании положений в слое l на основании вышележащих слоев и значений скорости эта матрица содержит все частные производные. Эту матрицу используют для построения ковариационной матрицыгеометрических положений в слое l, получаемых трассированием лучей. Сначала точно определяют неопределенности скорости и последовательно, слой за слоем, формируют ковариацию. Для первого слоя: где v является точно определенной ковариацией для скоростей, тогда как ,1 является ковариационной матрицей для пропикированных времен пробега в слое 1. Предполагается, что пропикированные времена пробега являются пространственно коррелированными в соответствии с их расстоянием от поверхности, и это представляют функцией пространственной корреляции и кронекеровым произведением для ,1. Более глубокие слои конструируют рекурсивно в соответствии с При l+1=m будет иметься полная ковариационная матрица для всех скоростей в слоях и геометрических положений в модели (северных, восточных и глубинных). Моделирование разрывов В этом разделе представлен способ объединения разрывов. В зависимости от геологических условий оценка положений разрывов в координатах глубины и неопределенностей их положений может быть сделана несколькими способами. Сосредоточим внимание на нормальных сбросах, то есть разрывах, которые наклонены в направлении горизонта. Для таких разрывов предположим, что точки, которые заполняют отверстия в горизонтах, становятся частью горизонтов, и их положения определяют, используя трассирование лучей. Эти положения разрывов называют "слившимися" точками. Остальные точки разрывов называют "неслившимися" точками. Неслившиеся точки располагают на основании глубины слившихся точек и положений на поверхности (в продольном направлении/поперечном направлении) относительно слившихся точек в данных о временах пробега сейсмических волн. Неопределенности положений разрывов оценивают в основном по распространению сейсмических ошибок, но также добавляют неопределенность, основанную на априорных суждениях интерпретатора. Кратко опишем математический подход, используемый для оценивания неслившихся точек в предположении, что положение слившихся точек достоверно получают в результате трассирования лучей. На основании набора слившихся точек вычисляют центральную точку (Nc, Ec, Dc), наклон и азимут разрыва. Все это получают путем простого вычисления среднего всех слившихся точек и основных компонент слившихся точек. Вычисление основных компонент протекает следующим образом. Пусть f обозначает ковариационную матрицу слившихся точек разрыва в координатах с направлением осей на север, восток и в глубину. Этот поднабор точек определяют пикингом точек, которые являются слившимися точками разрыва из числа всех точек. Эта матрица представляет собой подматрицу с индексами, пропикированными из m в уравнении (4). Основные компоненты определяютсясовместно со связанными с ними особыми значениямитак, что По основным компонентам можно вычислить азимут наклона и наклон по падению слившихся точек разрыва. Кроме того, при временной интерпретации для приписывания геометрических координат неслившимся точкам разрыва используют центральную точку и основные компоненты вместе с опорными положениями поверхности. Неслившиеся точки (Nf, Efr, Df) даются функциональной зависимостью,которая в краткой форме имеет вид: где опорные положения Nc, Ec, Dc поверхности в интерпретируемых данных о временах пробега сейсмических волн обрабатывают как фиксированные. Функция ff в этом случае представляет собой обращение результата вычисления основных компонент из слившихся точек. После оценивания этих точек разрыва геологические положения могут быть представлены G=(H,- 10018815F), где H - исходные точки горизонта без удаленных слившихся точек разрыва и где F - точки разрыва как слившиеся, так и неслившиеся. В дополнение к этому получают ассоциированную ковариационную матрицу для всех положений. Ковариационную матрицу для H составляют из набора распространения ошибок трассирования лучей, тогда как ковариационную матрицу для F составляют из набора, используя имитационные моделирования Монте-Карло для этого небольшого набора точек разрыва, основанного на уравнениях (5) и (6). Для точек разрыва также предполагают, что пикинг времен пробега является весьма недостоверным, и поперечным компонентам приписывают большую неопределенность, чтобы учесть эту неопределенность пикинга разрыва. Предполагается отсутствие взаимной корреляции между точками H горизонта и точками F разрыва. Корректировка модели на основе маркеров положения скважины После преобразования разрывов и горизонтов из временной области в глубинную с использованием скоростей сейсмических волн в систему вводят дополнительные результаты измерений их положений,основанные на скважинных измерениях. Этими основанными на дополнительных точках результатами измерений эффективно уменьшают неопределенность всей модели вследствие низкой их неопределенности по сравнению с неопределенностью исходной, преобразованной в глубинную область модели. Ограничение модели относительно скважинных измерений накладывают, используя способ корректировки методом наименьших квадратов, основанный на уравнениях условий. Все ошибки измерений и, следовательно, все линейные комбинации их предполагают гауссовыми. Подробно способ описан в приложении В. На основании этого способа получают уравнения:- ковариационная матрица начального вектора измерения; В - матрица ограничивающих уравнений;- оцененный вектор измерения (ограниченный путем использования матрицы В);- ковариационная матрица оцененного вектора измерения. Каждая включенная стохастическая переменная и, следовательно, любая линейная комбинация из них предполагаются нормально распределенными. Вектор L содержит результаты измерений трех видов: интервальные скорости, содержащиеся в векторе V,положения точек, образующих геологические поверхности, содержащиеся в векторе G,положения маркеров скважины, используемые для наложения ограничений на геологические поверхности, содержащиеся в W. Каждое полученное моделированием положение (маркеров скважины и геологических точек) состоит из трех координат Объединение результатов измерений трех видов в общий вектор где М представляет количество моделируемых скоростей (и горизонтов),S - суммарное количество геологических поверхностей (горизонтов и разрывов),n - количество геологических точек на каждой поверхности и Т - суммарное количество маркеров скважины. Суммарное количество геологических точек обозначено буквой О. Каждая строка В-матрицы состоит из коэффициентов одного уравнения ограничивающих условий,наложенных на набор результатов измерений, определяемых L0. Полные уравнения ограничивающих условий формулируются в соответствии с Матрица вращения играет важную роль в следующих разделах. Этой матрицей описывается преобразование между двумя вращающимися системами координат с одним и тем же началом. Поэтому точку и наоборот, точку в системе XYZ координат преобразуют в систему UYW при посредстве: Индивидуальные векторы-столбцы представляют единичные векторы системы UVW координат, при этом осями считаются XYZ. Вследствие этого последнего свойства векторыстолбцы матрицы вращения являются полезными для точного определения ограничивающих уравнений в произвольных пространственных направлениях. Корректировка за влияние скважины, ограниченная в вертикальном направлении В этом случае набор ограничивающих условий между координатами D маркеров скважины и их соответствующими геологическими общими точками задают только в вертикальном направлении. Для каждой пары точек ограничивающее уравнение можно представить в соответствии с: гдеPGk представляют собой координаты k-ой геологической точки в G иPW1 представляют собой координаты 1-го маркера скважины в векторе W маркера скважины. Наложение этих условий на В-матрицу дает: Каждая строка матрицы В 1 соответствует вектору измерения. Поскольку для интервальных скоростей в V ограничений не задают, М первых чисел каждого вектора-строки в В 1 полагают равными 0. Следующие 3 О места строки соответствуют геологическим точкам в G, при этом О является количеством геологических точек в G. Три места строки, согласующиеся с геологической точкой PGk в G,назначают для вектора Ck; остальные места, согласующиеся с G, полагают равными 0. Последние 3 Т места каждой строки в В 1 соответствуют маркерам скважины в W, где Т является количеством включенных маркеров скважины. Среди них только три места, соответствующих маркеру PW1, являются согласованными с вектором Cl, тогда как остальные места полагают равными 0. Суммарное количество строк вB1 равно количеству ограничений Т. Коррекция за влияние скважины, ограниченная вдоль нормали к поверхности Чтобы задать ограничение перпендикулярно к геологической поверхности в окрестности определенной геологической общей точки, используют собственный вектор n точек, ближайших к общей точке,точно определенный через матрицу R вращения: Ниже предполагается, что собственные векторы сортируют таким образом, что Rw является собственным вектором, соответствующим наименьшему относящемуся к нему собственному значению. Rw является приближенным единичным вектором, перпендикулярным к геологической поверхности. Поэтому умножение RWT на произвольный вектор дает компонент произвольного вектора в направлении Rw. Используя это, можно сформулировать условие между парой общих точек в виде: где PGk являются координатами k-ой геологической точки в G и PW1 координатами l-го маркера скважины в векторе W маркеров скважины. Объединение нескольких условий в общую матрицу В 1 дает: и эта матрица соответствует вектору измерения. М первых чисел каждого вектора- 12018815 строки в В 1 полагают равным 0, за которыми на каждой строке следуют 3O чисел, соответствующих геологическим точкам в G, при этом М является количеством интервальных скоростей в V, а О является количеством геологических точек в G. Три места строки, согласующиеся с геологической точкой PGk в G,назначают вектору RwkT; остальные места, согласующиеся с G, полагают равными 0. Последние 3 Т места каждой строки в В 1 соответствуют маркерам скважины в W, где Т является количеством включенных маркеров. Среди них только три места, соответствующие маркеру Pwl скважины, являются согласованными с вектором Rwl, тогда как остальные места полагают равными 0. Поскольку задано одно ограничение для каждого включенного маркера скважины, суммарное количество строк в B1 равно Т. Коррекция за влияние скважины, ограниченная в направлении воображаемых лучей В этом случае ограничения между координатами общих точек (то есть маркерами скважины и геологическими точками) задают в направлении угла падения луча трассы. Это ограничение можно выразить в соответствии с: где r=[r1 r2 r3]т является единичным вектором луча, падающего на поверхность, (XYZ)w и (XYZ)g являются координатами маркеров скважины и геологических точек, соответственно. Указанное выше ограничение может быть выражено следующей матрицей: где индексы k и l соответствуют в указанном порядке точкам PGk и PW1 вектора L. Т является количеством пар общих точек. Ограничения между разрывами и горизонтами Ограничения между разрывами и горизонтами можно добавлять, чтобы делать пересечения горизонтов и разрывов соответствующими друг другу и после обновления. Для единственной пары точек,состоящей из точки горизонта и точки разрыва, такое условие выражается в виде устанавливающем, что точка PHk горизонта на границе между горизонтом и разрывом должна быть идентична соответствующей точке PFl разрыва. Аналогичные ограничения на пересечениях разрывов с разрывами можно выразить в виде Набор таких ограничений можно добавить к В-матрице, образуя систему ограничивающих уравнений: Каждая строка матрицы В 2 соответствует вектору измерения. Первые М мест каждой строки, а также последние 3 Т полагают равными 0, поскольку интервальные скорости, а также маркеры скважины не включены в эти ограничения. М является количеством интервальных скоростей и Т является количеством маркеров скважины. Для каждой пары точек горизонта и разрыва имеются три ограничивающих уравнения; их коэффициенты представляют двумя единичными матрицами 33 в В 2. Суммарное количество строк в В 2 делают равным 3S. S является количеством пар точек горизонта/разрыва. Пикинг общих точек Как упоминалось ранее, корректировка методом наименьших квадратов основана на задании ограничений между маркерами скважины и геологическими точками. Маркер скважины и геологическая точка составляют общую точку. Для данного маркера скважины способ выбора наилучшей подходящей геологической точки может зависеть от применяемого принципа ограничения. В этом разделе будут представлены четыре способа пикинга общих точек. Три из этих способов особенно подходят для принципов ограничения, раскрытых выше. Четвертый способ можно применять для всех принципов ограничения. 1.1.1. Ограничение в вертикальном направлении Когда ограничения между маркером скважины и геологическими точками должны быть заданы в вертикальном направлении, геологическую точку с ближайшим поперечным эвклидовым расстоянием до маркера скважины используют в качестве общей точки. Поперечное расстояние dh вычисляют в соответствии с: где Nw и NG обозначают северные положения маркера скважины и геологической точки, соответственно. 1.1.2. Ограничения вдоль нормали к поверхности В этом случае в качестве геологической общей точки используют геологическую точку, лежащую ближе всего к приближенной нормали к геологической поверхности, проходящую через маркер скважины. Чтобы вычислить это расстояние, необходимо преобразовать геологические точки и маркер скважины в систему координат, в которой одна из осей лежит вдоль нормали к поверхности. Это делают, используя собственные векторы h геологических точек, ближайших к поверхности, в качестве матрицы вращения, для преобразования между системой NED и системой UVW координат, в которых направление W лежит вдоль нормали к поверхности. Матрицу вращения вычисляют следующим образом: где Предполагается, что векторы-столбцы RNEDUVW сортируют таким образом, что вектор Rw является собственным вектором, соответствующим наименьшему собственному значению. При преобразованиях среднюю точку из n геологических точек, ближайших к маркеру Rw, используют в качестве начальной для системы UVW координат. Поэтому преобразования произвольных точек PG и Pw в систему UVW формулируют как: Затем перпендикулярное расстояние duv между нормалью к поверхности, проходящей через маркер скважины и различные геологические точки, вычисляют в соответствии с формулой: 1.1.3. Ограничения в направлении воображаемого луча Подходящую геологическую точку можно найти путем сравнения перпендикулярных расстояний между реальной отбивкой скважины и всеми ближайшими трассами падающих лучей геологических точек. В таком случае геологическая точка, соответствующая по перпендикулярному направлению ближайшей трассе луча, будет кандидатом на общую точку. Нижеследующий способ можно использовать для нахождения кратчайшего перпендикулярного расстояния между отбивкой скважины и ближайшими трассами падающих лучей. Сначала путем сравнения горизонтальных координат находят поднабор геологических точек, ближайших к маркеру скважины. Затем вычисляют наикратчайшее перпендикулярное расстояние от отбивки скважины до каждого единичного вектора трассы луча. Пусть маркер скважины и геологическая точка выражены в соответствии с: Вектор от маркера Pw скважины до геологической точки PG дается формулой: Перпендикулярное расстояние D от маркера скважины до единичного вектора го луча является просто длиной векторного произведения Эту длину можно вычислить по формуле: Описанная выше процедура должна повторяться для всех маркеров скважины в реальной области. 1.1.4. "Наиболее вероятная" геологическая общая точка В этом способе эллипсоиды неопределенности маркера скважины и геологических точек используют для выбора "наиболее вероятной" геологической общей точки. Взвешенную величину расстояния вычисляют по формуле: Суммирование ковариационной матрицы w маркера скважины и ковариационной матрицы G геологической точки возможно, поскольку при первоначальной интерпретации сейсмических данных предполагают отсутствие корреляции с маркером скважины. Модель неопределенности маркера скважины Координаты маркеров скважины являются значимыми входными данными. Другими значимыми входными данными являются дисперсии координат маркеров скважины и ковариации между ними. Ствол скважины содержит несколько точек наблюдений и некоторые из этих точек наблюдений выбирают в качестве маркеров скважины. Координаты маркеров скважины вычисляют на основании результатов инклинометрических и глубинных измерений, выполняемых в нескольких точках вдоль ствола скважины. Инклинометрические измерения между точками наблюдений являются коррелированными. Это также наблюдается в случае измерений глубины. Эти корреляции должны учитываться для гарантии надлежащего распространения дисперсии и ковариационной матрицы. Моделирование дисперсий и ковариаций маркеров скважины Глубинные измерения вносят значительный вклад в неопределенность положения ствола скважины при выполнении исследований магнитными и гироскопическими приборами. Считается, что корреляции между результатами глубинных измерений являются наиболее значимыми корреляциями при исследованиях в стволе скважины. Другим источником сильных корреляций является ошибка определения углового отклонения скважины. Подробный обзор наиболее значимых источников ошибок при глубинных измерениях дал EksethR., 1998. Нижеследующая процедура является подходящей для исследования эффектов глубинных корреляций. Для прогнозирования корреляционного поведения результатов глубинных измерений между точками наблюдений вдоль ствола скважины можно использовать корреляционную функцию. Корреляционную функцию можно выразить, например, в членах экспоненциальной функции: где ij является коэффициентом корреляции,представляет подходящую длину корреляции и Di иDj являются измеряемыми глубинами в точках i и j, соответственно. Длинакорреляции определяется как длина, необходимая, чтобы корреляция между двумя маркерами скважины снижалась ниже определенного значения. Ковариацию дующей формулой: между маркерами i и j скважины можно прогнозировать в соответствии со сле где ij является коэффициентом корреляции, а ii и jj представляют дисперсии маркеров скважины под номером i и номером j, соответственно. Список литературыTorkildsen Т., 2006, Method of combining spatial models, US Patent 7149672 B2 Alkhalifa Т., Lamer K.,1994, Migration error in transversely isotropic media, Geophysics (59), 1405-1418. Приложение А. Трассирование воображаемых лучей Трассирование воображаемых лучей определяется началом вертикального хода луча на поверхности и применением закона Снелла на границах раздела. На каждой границе двух горизонтов l и l+1 и для каждой точки k=1,K,nh для трассирования лучей необходимо иметь следующее: 1) Единичный вектор падающего луча: 2) Единичный нормальный вектор K границы 1: и k является точно определенной окрестностью точки k. 3) Угол падения в точке k слоя l: 5) Единичный вектор передачи в точке k в слой l+1: где скалярные коэффициенты перед uk,i и uk,n оценивают при условии гарантии, что являются справедливыми, как и sin2=1-cos2 и закон Снелла из уравнения (10). 6) Полученная прогнозированием точка k в слое l+1: где компоненты единичного вектора передачи даются формулой Этапы (1-6), описанные в уравнениях (5-13), в краткой форме можно записать как: где функцией обобщаются все зависимости. Приложение В. Вывод формул корректировки методом наименьших квадратов В.1. Определения Измеряемые значения: Ошибки измерений считаются нормально распределенными, и поэтому все линейные комбинации ошибок измерений также распределены нормально. Веса измерений: Дополнительная матрица: QLL-PLL-1. Если измеряемые значения взвешивают, используя их исходные неопределенности измерений, тоQLL=PLL-1=LL, где LL обозначает исходную ковариационную матрицу измеряемых значений. Неизвестные: Невязки: =L-L истинное. Модель: АХ=L истинное = с, что дает= AX - F, где F = L+c. с является постоянным вектором. В статистических терминах из [2]: Уравнение условия: BX-Wc=0, где Wc - постоянный вектор. Закон распространения ошибки: если имеется модель у=Ах, то В.2. Образование нормальных уравнений Используя уравнение условия, можно сконструировать вспомогательную функцию h, в которой на взвешенную сумму квадратов налагают условия в соответствии с уравнением условия, используя множители Лагранжа:K является вектором множителей Лагранжа. Заменадает: Используя производные вспомогательной функции по неизвестным K и X, можно образовать систему нормальных уравнений, содержащих оценки неизвестных величин K и X методом наименьших квадратов: Преобразование нормальных уравнений в матричное уравнение предоставляет прямой путь вычисления При использовании закона распространения ошибки дополнительная матрица для В.3. Прямое вычисление оценки для X Поскольку для нас представляют интерес только чав с: Подстановка этого результата в уравнение для В.4. Прямое вычисление оценки для Qxx Применение закона распространения ошибки к: дает В.5. Статистическая модель: X-L=0. Обратимся к статистической модели: AX-L=c, из которой следует =AX-F, где F=L+c. с является постоянным вектором. Ее можно легко преобразовать в модель X-L=0, задав А=I иF=L и N0=PLL. Еще желательно учесть уравнение условия: BX-Wc-0 . Применение этих изменений к: ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ формирования геологической модели области среды, содержащий этапы, на которых:i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;iv) вычисляют неопределенности положений в трех измерениях по меньшей мере некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; иv) формируют геологическую модель из положений в трех измерениях множества точек области, определенных на этапе (iii) с неопределенностями положений в трех измерениях, вычисленными на этапе (iv) . 2. Способ по п.1, в котором, по меньшей мере, некоторые из точек располагают на по меньшей мере одной границе раздела, идентифицированной по сейсмическим данным, между подобластями области различных скоростей сейсмических волн. 3. Способ по п.1, в котором, по меньшей мере, некоторые из точек располагают на разрывах, идентифицированных по сейсмическим данным. 4. Способ по п.1, в котором неопределенность времени пробега определяют по длине волны сейсмической волны, используемой для получения сейсмических данных. 5. Способ по п.1, в котором неопределенность скорости определяют на основании сведений о геологии области. 6. Способ по п.1, в котором на этапе (iii) определяют положение каждой из точек с помощью одной из функций: положения на вышележащей границе раздела, где луч, падающий на точку, пересекает вышележащую границу раздела; скорости сейсмической волны от положения до точки, полученной на основании скоростной модели; и времени пробега от положения до точки, полученной по сейсмическим данным. 7. Способ по п.6, в котором на этапе (iv) осуществляют дифференцирование функции. 8. Способ по п.7, в котором функция включает в себя первую подфункцию, представляющую закон Снелла, и вторую подфункцию, представляющую наклон при положении, и на этапе (iv) определяют производные первой и второй подфункций. 9. Способ по п.1, в котором этап (v) включает в себя приписывание корреляций среди, по меньшей мере, некоторых из точек. 10. Способ по п.1, в котором дополнительно приписывают корреляции среди значений скорости в скоростной модели. 11. Способ по п.1, в котором геологическая модель представляет собой первую геологическую модель, и способ дополнительно содержит этапы, на которых:vi) подготавливают получаемые не сейсмическим способом трехмерные данные о положении и трехмерные данные о неопределенности положения вокруг области; иvii) корректируют первую геологическую модель с помощью данных, подготовленных на этапе (vi),чтобы получить вторую геологическую модель. 12. Способ по п.11, в котором получаемые не сейсмическим способом данные содержат данные о маркерах скважины. 13. Способ по п.11, в котором на этапе (vii) осуществляют выбор по меньшей мере одной общей точки из области, которая является общей для первой геологической модели и для получаемых не сейсмическим способом данных, и определяют положение и неопределенность положения общей точки во второй геологической модели на основании положений и неопределенностей положений общей точки в первой геологической модели и в получаемых не сейсмическим способом данных. 14. Способ по п.13, в котором по меньшей мере одна общая точка представляет общие или граничащие геологические признаки. 15. Способ по п.14, в котором получаемые не сейсмическим способом данные содержат данные о маркерах скважины и по меньшей мере одна общая точка представляет место на одной границе раздела в первой геологической модели и место в получаемых не сейсмическим способом данных, где скважина проходит через границу раздела. 16. Способ по п.15, в котором на этапе (vii) перемещают место общей точки в первой геологической модели, по существу, параллельно пути луча или на соседнее место. 17. Способ по п.14, в котором по меньшей мере одна общая точка представляет место на разрыве в первой модели и место в получаемых не сейсмическим способом данных, где скважина проходит через разрыв. 18. Способ по п.17, в котором на этапе (vii) перемещают место общей точки в первой геологической модели, по существу, перпендикулярно к поверхности разрыва. 19. Способ по п.16, в котором дополнительно обновляют получаемые не сейсмическим способом данные путем перемещения места общей точки в получаемых не сейсмическим способом данных в направлении, по существу, противоположном направлению перемещения в первой геологической модели. 20. Способ по п.18, в котором дополнительно обновляют получаемые не сейсмическим способом данные путем перемещения места общей точки в получаемых не сейсмическим способом данных в направлении, по существу, противоположном направлению перемещения в первой геологической модели. 21. Способ по п.11, в котором на этапе (vi) обеспечивают получаемые не сейсмическим способом данные о скорости и данные о неопределенности скорости вокруг области. 22. Способ по п.21, в котором дополнительно образуют и/или обновляют скоростную модель в соответствии с получаемыми не сейсмическим способом данными о скорости и неопределенности скорости. 23. Способ по п.11, в котором этап (vii) выполняют при наличии ограничения, такого, что пересечения граница/разрыв сохраняются во второй геологической модели. 24. Способ по п.13, в котором на этапе (vii) осуществляют выбор множества общих точек и коррек- 19018815 тировку первой геологической модели за один этап. 25. Способ по п.18, в котором на этапе (vii) осуществляют корректировку первой геологической модели на первом этапе относительно по меньшей мере одной общей точки на границе и затем на втором этапе относительно по меньшей мере одной общей точки на разрыве. 26. Способ по п.11, в котором на этапе (vii) осуществляют корректировку первой геологической модели рекурсивно слой за слоем. 27. Компьютер, содержащий программу для выполнения способа образования геологической модели области среды, и этот способ содержит этапы, на которых:i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;iv) вычисляют неопределенности положений в трех измерениях, по меньшей мере, некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; иv) формируют геологическую модель из положений в трех измерениях множества точек области,определенных на этапе (iii) с неопределенностями положений в трех измерениях, вычисленными на этапе (iv). 28. Считываемый компьютером носитель данных, содержащий программу, выполненную с возможностью программирования компьютера для выполнения способа образования геологической модели области среды, и этот способ содержит этапы, на которых:i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;iv) вычисляют неопределенности положений в трех измерениях, по меньшей мере, некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; иv) формируют геологическую модель из положений в трех измерениях множества точек области,определенных на этапе (iii) с неопределенностями положений в трех измерениях, вычисленными на этапе (iv). 29. Способ бурения скважины в области геологической среды на основе геологической модели области среды, содержащий этапы, на которых:i) обеспечивают сейсмические данные, получаемые из области и включающие в себя неопределенность времени пробега сейсмической волны;ii) обеспечивают сейсмическую скоростную модель области, включающую в себя неопределенность скорости;iii) выполняют трассирование воображаемых лучей по сейсмическим данным, используя скоростную модель для определения положений в трех измерениях множества точек области;iv) вычисляют неопределенности положений в трех измерениях, по меньшей мере, некоторых точек на основании неопределенности времени пробега, неопределенности скорости и неопределенности направления распространения луча; иv) формируют геологическую модель из положений в трех измерениях множества точек области,определенных на этапе (iii) с неопределенностями положений в трех измерениях, вычисленными на этапе (iv), и управляют бурением в соответствии с геологической моделью.
МПК / Метки
Метки: модели, геологической, формирование
Код ссылки
<a href="https://eas.patents.su/26-18815-formirovanie-geologicheskojj-modeli.html" rel="bookmark" title="База патентов Евразийского Союза">Формирование геологической модели</a>
Предыдущий патент: Термофильный микроорганизм для повышенной продукции этанола из крахмалсодержащего сырья и способ обеспечения повышенной продукции этанола при его использовании
Следующий патент: Способы перфорирования с использованием вязкоупругих поверхностно-активных текучих сред и связанные с ними составы
Случайный патент: Флуоресцентный контрастный агент для ближней инфракрасной области спектра












