Устройство передачи, устройство приема, способ передачи, способ приема и способ для формирования многомерных созвездий
Формула / Реферат
1. Устройство передачи для передачи блока данных по множеству каналов передачи, причем устройство передачи содержит
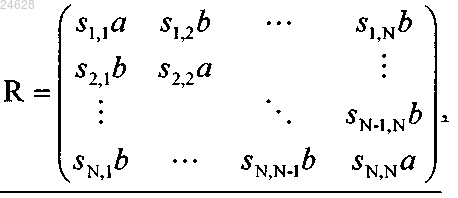
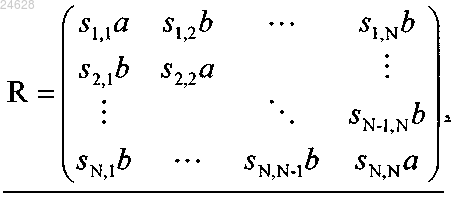
модулятор, функционирующий с возможностью формирования одной из множества точек созвездия, являющегося результатом поворота исходного созвездия, в соответствии с блоком данных, который подлежит передаче, причем каждая из множества точек упомянутого созвездия, являющегося результатом поворота созвездия, имеет N компонентов, причем каждая из множества точек исходного созвездия имеет N компонентов, причем поворот созвездия представлен матрицей R размером N´N; и
передатчик, функционирующий с возможностью передачи каждого компонента сформированной точки созвездия по разному одному из множества каналов передачи,
причем N кратно четырем,
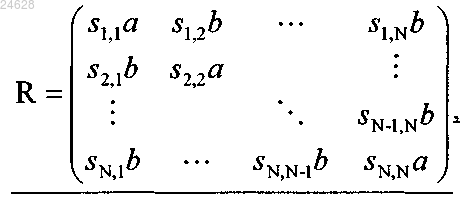
где а и b обозначают вещественные параметры,
каждое знаковое значение si,j удовлетворяет
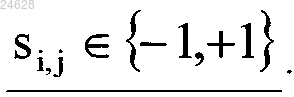
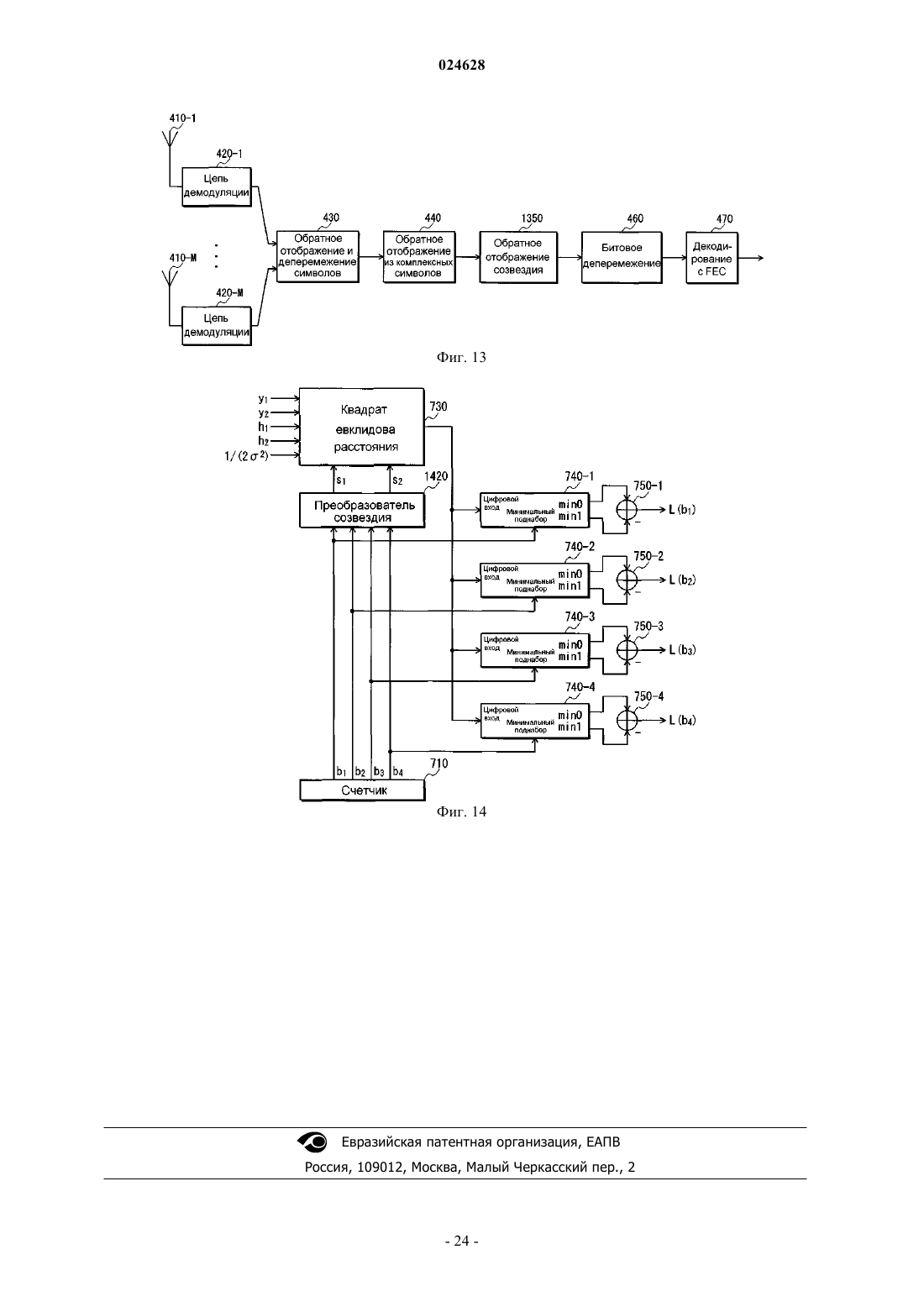
2. Устройство приема для приема блока данных по множеству каналов передачи, причем устройство приема содержит
приемник, функционирующий с возможностью приема N сигналов компонентов по множеству каналов передачи; и
демодулятор, функционирующий с возможностью демодуляции принятых N сигналов компонентов на основе созвездия, являющегося результатом поворота исходного созвездия, причем каждая из множества точек упомянутого созвездия, являющегося результатом поворота созвездия, имеет N компонентов, причем каждая из множества точек исходного созвездия имеет N компонентов, причем поворот созвездия представлен матрицей R размером N´N,
причем N кратно четырем,
где а и b обозначают вещественные параметры,
каждое знаковое значение si,j удовлетворяет
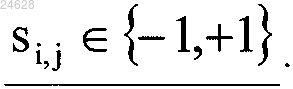
3. Способ передачи для передачи блока данных по множеству каналов передачи, причем способ передачи содержит этапы, на которых
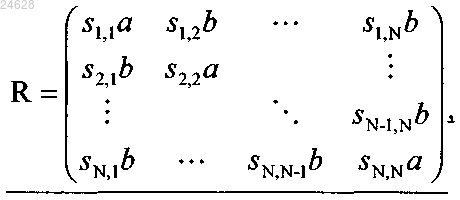
формируют одну из множества точек созвездия, являющегося результатом поворота исходного созвездия, в соответствии с блоком данных, который подлежит передаче, причем каждая из множества точек упомянутого созвездия, являющегося результатом поворота созвездия, имеет N компонентов, причем каждая из множества точек исходного созвездия имеет N компонентов, причем поворот созвездия представлен матрицей R размером N´N; и
передают каждый компонент сформированной точки созвездия по разному одному из множества каналов передачи,
причем N кратно четырем,
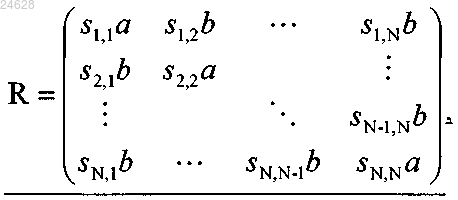
где а и b обозначают вещественные параметры,
каждое знаковое значение si,j, удовлетворяет
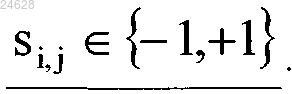
4. Способ приема для приема блока данных по множеству каналов передачи, причем способ приема содержит этапы, на которых
принимают N сигналов компонентов по множеству каналов передачи;
демодулируют принятые N сигналов компонентов на основе созвездия, являющегося результатом поворота исходного созвездия, причем каждая из множества точек упомянутого созвездия, являющегося результатом поворота созвездия, имеет N компонентов, причем каждая из множества точек исходного созвездия имеет N компонентов, причем поворот созвездия представлен матрицей R размером N´N,
причем N кратно четырем,
где а и b обозначают вещественные параметры,
каждое знаковое значение si,j удовлетворяет
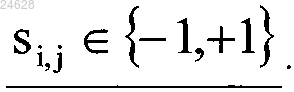
5. Способ цифровой модуляции в системе передачи данных, причем способ содержит этапы, на которых
принимают множество векторов в N-мерном векторном пространстве, связанном с исходным созвездием; и
получают множество точек созвездия N-мерного созвездия, являющегося результатом поворота созвездия, в соответствии с множеством принятых векторов, причем поворот созвездия приспособлен для увеличения минимального количества разных значений в компонентах любых двух различных точек N-мерного созвездия относительно минимального количества разных значений в компонентах любых двух различных принятых векторов, причем поворот созвездия представлен матрицей R размером N´N,
где а и b обозначают вещественные параметры,
каждое знаковое значение si,j удовлетворяет
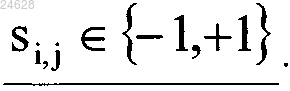
Текст
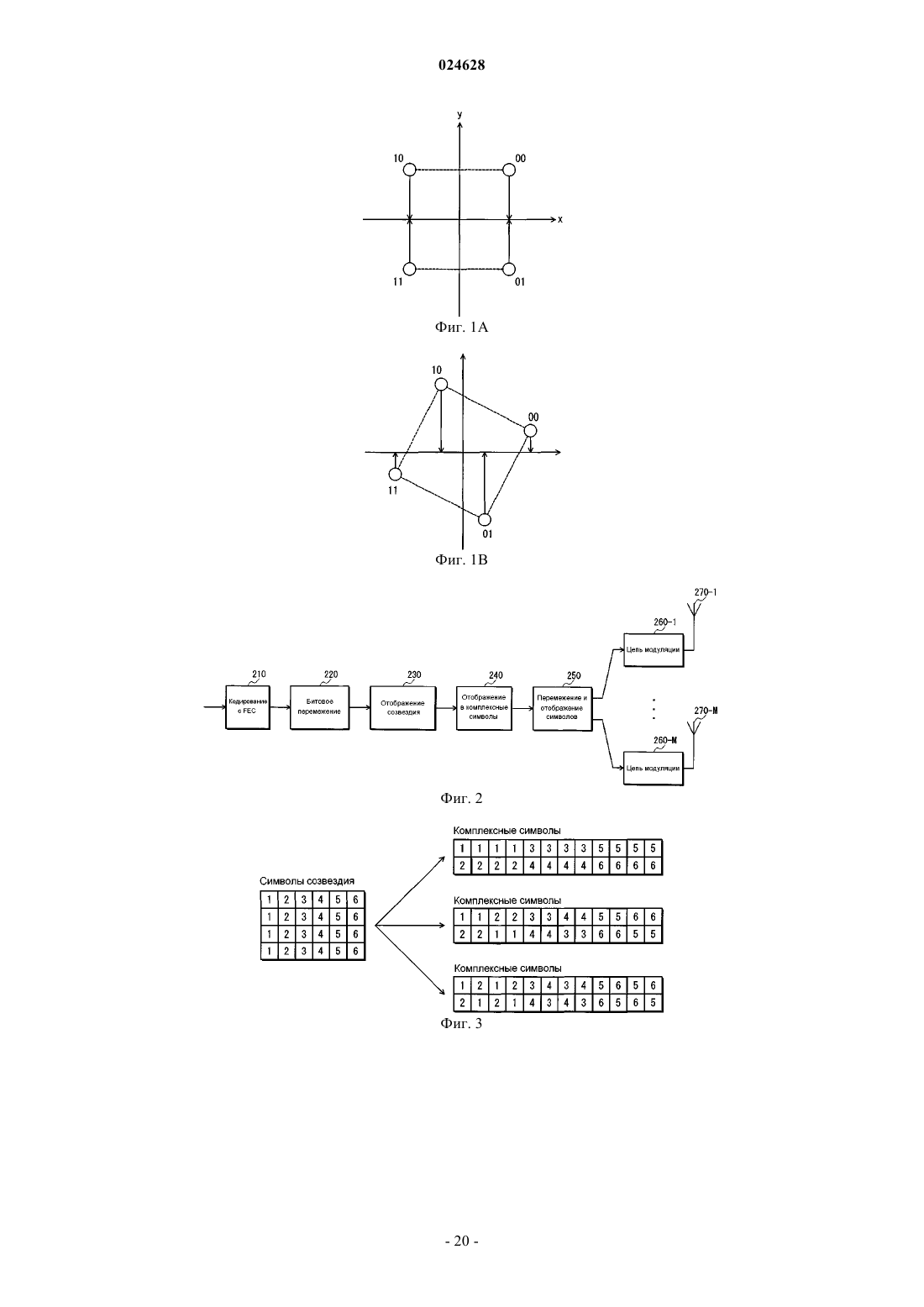
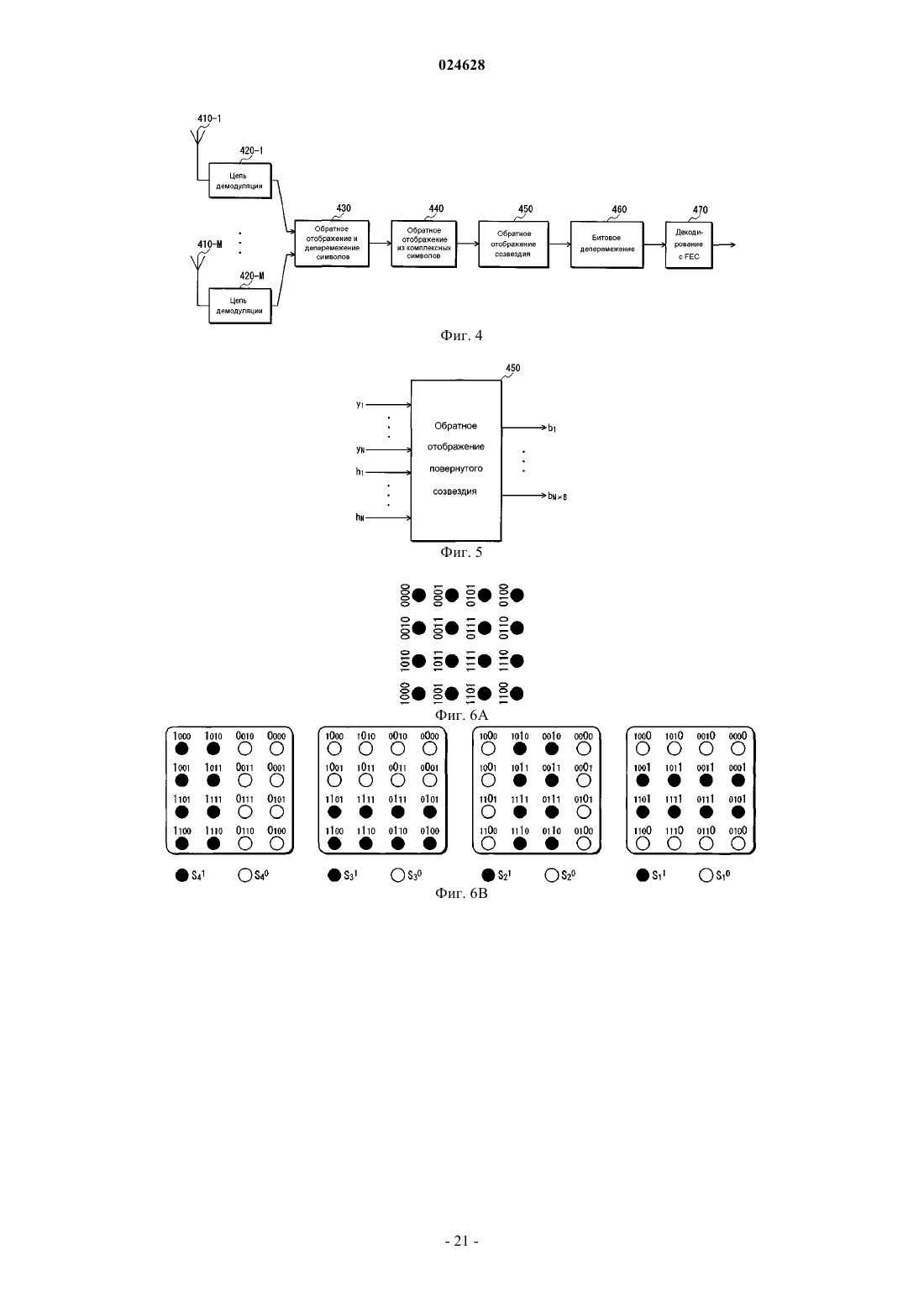
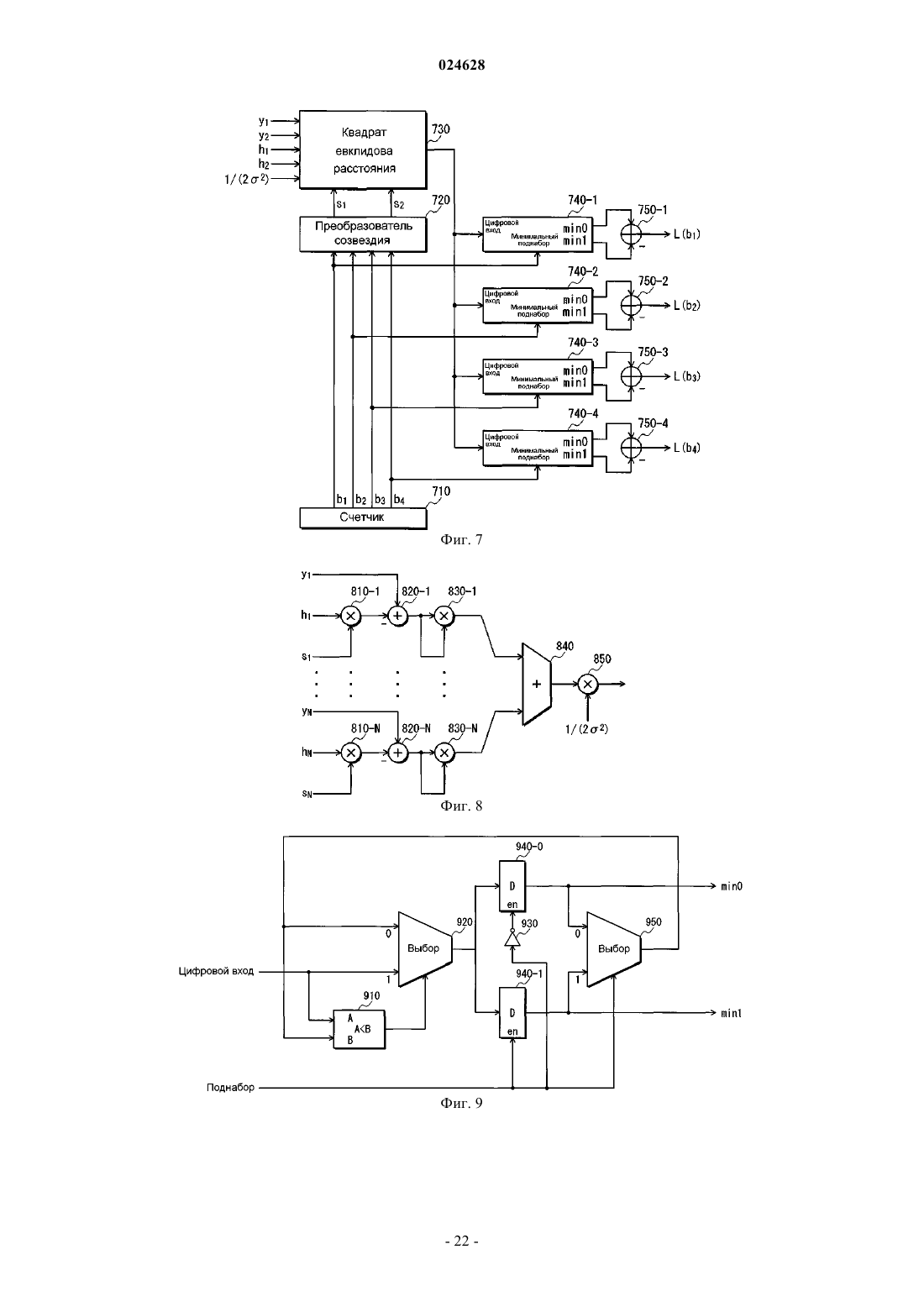
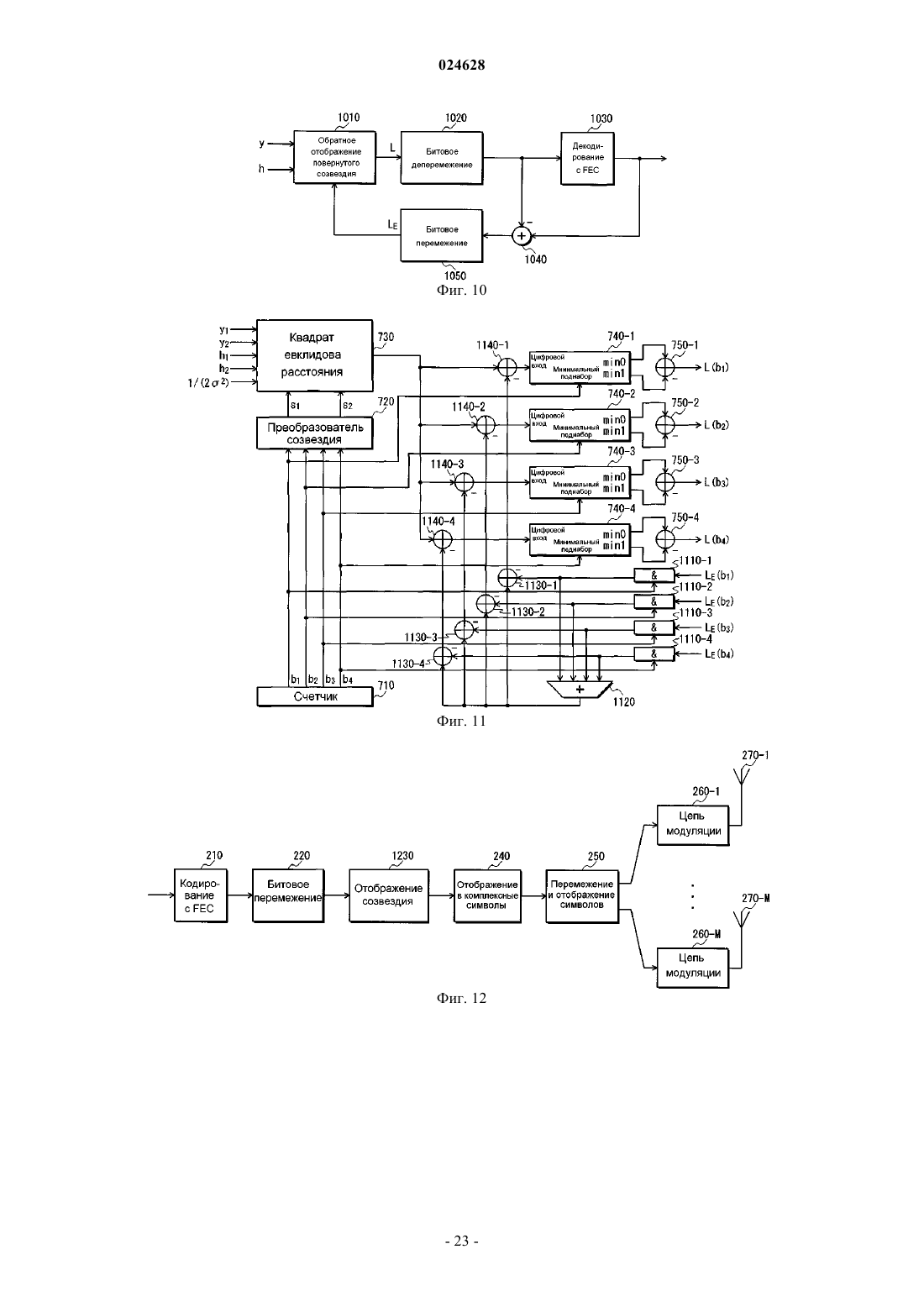
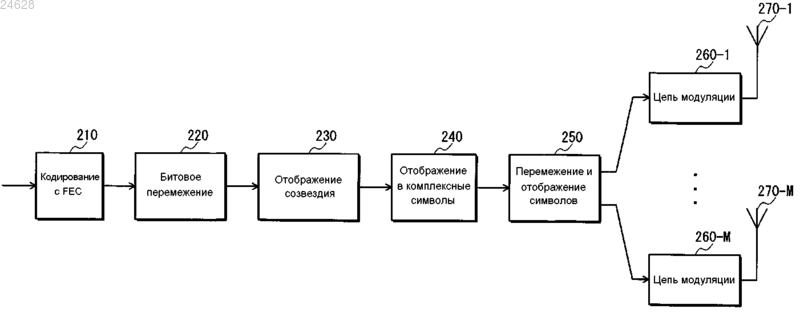
Изобретение относится к цифровой передаче данных и представляет эффективный способ для формирования многомерных созвездий для цифровой модуляции данных с высокой степенью модуляционного разнесения, способ передачи и приема данных на основе таких созвездий и соответствующее устройство. Это достигается путем рассмотрения только многомерных матриц вращения со всеми элементами на диагонали, имеющими одинаковое первое абсолютное значение,и со всеми остальными элементами, имеющими одинаковое ненулевое второе абсолютное значение. Таким образом, можно формировать многомерные матрицы вращения, имеющие только один независимый параметр и структуру, которая регулярна, насколько это возможно. Независимый параметр может конфигурироваться, чтобы минимизировать вероятность ошибки для различных размеров созвездий. САН ПЭТЕНТ ТРАСТ (US) Петров Михаил (DE), Кимура Томохиро (JP) Медведев В.Н. (RU) УСТРОЙСТВО ПЕРЕДАЧИ, УСТРОЙСТВО ПРИЕМА, СПОСОБ ПЕРЕДАЧИ, СПОСОБ ПРИЕМА И СПОСОБ ДЛЯ ФОРМИРОВАНИЯ МНОГОМЕРНЫХ СОЗВЕЗДИЙ Область техники Настоящее изобретение относится к цифровой передаче данных, в частности к способам для формирования многомерных созвездий для цифровой модуляции данных, способам для модулирования и передачи данных на основе многомерных созвездий и соответствующему устройству. Предшествующий уровень техники Замирание является одной из насущных проблем в системах связи. Оно представляет собой случайные колебания амплитуды принятого сигнала вследствие многолучевого распространения. Если распространение задержек канала больше периода символа у сигнала, то замирание также является избирательным по частоте. Амплитуда замирания обычно приблизительно аппроксимируется распределением Релея. Такое замирание называется релеевским замиранием. В системах цифровой связи информация кодируется в виде последовательности символов, принадлежащих дискретному алфавиту, называемому созвездием. Такое созвездие имеет N измерений и кодирует В информационных битов на каждое измерение. Поэтому количество возможных значений, также называемых точками созвездия, равно 2NB. Количество битов на каждое измерение В непосредственно определяет спектральную эффективность передачи, задаваемую в битах/Гц. Количество измерений N не оказывает влияние на спектральную эффективность. Примерное созвездие при N=2 и В=1 иллюстрируется на фиг. 1 А. Традиционно, например, в созвездии с квадратурной амплитудной модуляцией (QAM), показанном на фиг. 1 А, каждый переданный бит влияет только на одно измерение. Ссылаясь на фиг. 1 А, "b1" каждой точки созвездия "b1b2" (= "00", "01", "10" и "11") влияет только на измерение, представленное горизонтальной осью, тогда как "b2" каждой точки созвездия "b1b2" влияет только на измерение, представленное вертикальной осью. Если измерение, затронутое переданными битами, подвергается глубокому замиранию, то все биты, которые модулируют это измерение, будут крайне ненадежными, что увеличивает вероятность ошибки. Этот эффект иллюстрируется ошибками на фиг. 1 А. Например, если замирает канал,представленный вертикальной осью, то точки созвездия "00", "01", "10" и "11" приблизятся к горизонтальной оси (по сплошным стрелкам на фиг. 1 А). В результате точки созвездия "00" и "01", а также точки созвездия "10" и "11" будут неразличимы. Если созвездие изменяется таким образом, что каждый бит влияет на все измерения, то устойчивость к замиранию увеличивается. Глубокое замирание по одному из измерений повлияет на все биты созвездия; однако этот эффект не был бы таким вредным, как в традиционном случае, так что вероятность ошибки в среднем уменьшается. В литературе это называется модуляционным разнесением. Повернутые созвездия. Одним способом для достижения модуляционного разнесения является поворот (гиперкубического) созвездия для распространения эффекта замирания канала по всем его измерениям. Это иллюстрируется на фиг. 1 В для случая, где N=2 и В=1. Например, как показано на фиг. 1 В, если замирает канал, представленный вертикальной осью, то точки созвездия "00", "01", "10" и "11" приблизятся к горизонтальной оси (по сплошным стрелкам на фиг. 1 В). Однако эти точки созвездия по-прежнему будут различимы в измерении, представленном горизонтальной осью. По существу, точки созвездия "00", "01", "10" и "11" остаются различимыми даже после глубокого замирания канала, представленного вертикальной осью. Многомерное вращение может достигаться путем умножения N-элементного вектора сигналов на квадратную матрицу NN. Необходимым и достаточным условием, чтобы квадратная матрица была матрицей вращения (или матрицей отражения), является ее ортогональность, т.е. она должна удовлетворять уравнению в нижеследующем выражении 1.[Выражение 1] Отметим, что в вышеприведенном выражении 1 матрица является квадратной матрицей, матрица является транспонированной матрицей матрицы , а матрица является единичной матрицей. Это означает, что в отношении вышеприведенного выражения 1 векторы строки/столбца должны быть ортогональными единичными векторами, т.е. удовлетворять уравнению в следующем выражении 2.. Это сохраняет евклидово расстояние между любыми двумя точками созвездия и обеспечивает, что не затрагивается производительность в каналах с аддитивным белым гауссовским шумом (каналахAWGN). Очевидно, что не все вращения дают эффект улучшенного модуляционного разнесения. Из NPL 1 известно, что оптимальный угол поворота для 16-QAM удовлетворяет уравнению, показанному в следующем выражении 3. Соответствующая 2D (двумерная) матрица вращения удовлетворяет уравне-1 024628 Нахождение оптимального вращения для созвездий более чем с двумя измерениями является более сложным, потому что отсутствует единый параметр оптимизации, например параметр, относящийся к углу поворота в двумерном созвездии. В случае 4D (четырехмерного) созвездия, например, существует шесть независимых углов поворота, каждый со своей матрицей частичного вращения. Углы частичного поворота также называются углами Гивенса в NPL 2. Итоговая четырехмерная матрица вращения получается путем умножения шести матриц вращения Гивенса, а именно шести матриц, показанных в следующем выражении 5. Из NPL 2 известно, что оптимизация может осуществляться по вектору, содержащему шесть элементов, показанных в выражении 6.[Выражение 6] В соответствии с NPL 2 результирующие оптимальные углы поворота для четырехмерного созвездия с 2 битами на измерение имеют значения, показанные в следующем выражении 7. Недостатком этого способа является количество параметров, особенно для большого количества измерений. Для N измерений количество углов частичного поворота равно количеству возможных сочетаний двух из набора N, т.е. значению, заданному следующим выражением 8. Поэтому количество углов поворота увеличивается пропорционально квадрату количества измерений, так что проблема оптимизации становится очень сложной, когда количество измерений большое.NPL 3 раскрывает два разных подхода, опирающихся на использование алгебраической теории чисел, которые обладают преимуществом в сниженном количестве параметров. Первый подход делает возможным создание матриц вращения путем применения "канонического вложения" к полю алгебраических чисел. Предлагаются два способа. Первый способ создает решетки с разнесением L=N/2 для количества измерений N=2e23e3, причем е 2, е 3=0, 1, 2, , . Разнесение означает минимальное количество разных значений в компонентах любых двух различных точек созвездия. Второй способ создает решетки с разнесением L=N. Возможные значения N очень ограничены, например 3,5, 9, 11 и 15. Разновидность этого способа для формирования N-мерных повернутых созвездий также известна изNPL 3. Матрица вращения выражается следующим выражением 9. Отметим, что буква "Т" в верхнем индексе обозначает транспонирование матрицы. Для N=4 значение матрицы вращения задается следующим выражением 10. Хотя результирующая матрица вращения является матрицей вращения, которая ортогональна для любого N, полное модуляционное разнесение достигается, только когда N является степенью двойки. Каждый из этих способов может гарантировать определенную степень разнесения. Однако результирующая матрица вращения является фиксированной, не имеющей параметра, который дает возможность оптимизации для разных размеров созвездий. Поэтому серьезным недостатком этих способов является то, что эффект модуляционного разнесения нельзя максимизировать в соответствии с разными размерами созвездий. Второй подход сначала создает матрицы вращения с двумя и тремя измерениями, которые могут использоваться в качестве базовых матриц для создания матриц с большим количеством измерений, используя многоуровневое разложение наподобие адамарова, показанное в следующем выражении 11. Базовые двумерные и 3D (трехмерные) матрицы вращения имеют один независимый параметр, который выбирается так, чтобы рабочее расстояние созвездия максимизировалось. Четырехмерная матрица вращения создается из двух двумерных матриц вращения в соответствии с вышеприведенным выражением 11. Из-за относительно небольшого измерения можно найти алгебраическое соотношение между параметрами двух двумерных матриц вращения, чтобы рабочее расстояние максимизировалось. Для большего числа измерений такая оптимизация становится трудной для решения, что является основным недостатком второго подхода. Отображение компонентов созвездия для обеспечения независимого замирания. Другой аспект касается разделения и отображения N измерений повернутого созвездия так, чтобы они испытывали независимое замирание. Это ключевой аспект, необходимый для достижения предполагаемой производительности разнесения.N компонентов созвездия, которые получаются путем разделения N-мерного повернутого созвездия на основе каждого измерения, могут передаваться на разных временных слотах, частотах, антеннах передатчика или их сочетаниях. Возможна дополнительная обработка сигналов перед передачей. Критический аспект состоит в том, что замирание, испытываемое каждым из N измерений, должно отличаться или в идеале не коррелировать с замиранием, испытываемым любым другим из N измерений. Распространение N измерений на разные временные слоты, частоты и антенны может достигаться,например, посредством подходящего перемежения и отображения. Отображение компонентов созвездия в переданные комплексные ячейки. Другой аспект касается отображения N вещественных измерений повернутого созвездия в комплексные символы для передачи. Чтобы обеспечить желаемое разнесение, N измерений должны быть отображены в разные комплексные символы. Комплексные символы затем распространяются, как описано раньше, например, посредством перемежения и отображения, чтобы при приеме замирание, испытываемое каждым из N измерений, не коррелировало с замиранием любого другого из N измерений. На фиг. 2 показана блок-схема устройства передачи. Устройство передачи состоит из кодера 210 FEC, битового перемежителя 220, преобразователя 230 повернутого созвездия, преобразователя 240 комплексных символов, перемежителя/преобразователя 250 символов, цепей модуляции с 260-1 по 260-М и антенн передатчика с 270-1 по 270-М. Кодер 210 FEC выполняет кодирование с прямым исправлением ошибок (FEC) над входными данными. Отметим, что лучшими кодами FEC, известными до настоящего времени, которые также больше всего используются в новых стандартах, являются турбокоды и коды с низкой плотностью проверок на четность (LDPC). Битовый перемежитель 220 выполняет битовое перемежение над входными данными от кодера 210FEC. Здесь битовое перемежение может быть блочным перемежением или сверточным перемежением. Преобразователь 230 повернутого созвездия отображает входные данные из битового перемежителя 220 в повернутое созвездие. Как правило, входными данными в преобразователь 230 повернутого созвездия являются выходные данные кодера 210 FEC через битовый перемежитель 220, который выполняет необязательное битовое перемежение. Битовое перемежение обычно необходимо, когда имеется более одного бита на измерение(В 1). Кодирование с FEC, выполненное кодером 210 FEC, вносит избыточные биты управляемым способом, так что накапливающиеся ошибки можно исправить в устройстве приема. Хотя общая спектральная эффективность уменьшается, передача в целом становится устойчивее, т.е. частота появления ошибочных битов (BER) снижается гораздо быстрее вместе с отношением сигнал/шум (SNR). Отметим, что касательно исходного отображения информационных битов в неповернутых гиперкубических созвездиях каждое измерение модулируется отдельно с помощью В битов, используя либо двоичное отображение, либо отображение Грея, поэтому количество дискретных значений равно 2 В, а количество точек созвездия равно 2BN. Преобразователь 240 комплексных символов отображает каждый из N компонентов созвездия, которые представляют собой символы N-мерного повернутого созвездия, введенные из преобразователя 230 повернутого созвездия, в разные комплексные символы. Существует несколько возможностей для отображения, выполненного преобразователем 240 комплексных символов, т.е. отображения каждого из N компонентов созвездия, которые представляют символы N-мерного повернутого созвездия, в разные комплексные символы. Некоторые из таких возможностей иллюстрируются на фиг. 3. Неотъемлемой функцией преобразователя 240 комплексных символов является отображение каждого из N компонентов созвездия в одном символе повернутого созвездия в разные комплексные символы. В качестве примера фиг. 3 показывает случай четырех измерений. Ссылаясь на фиг. 3, ячейки, показывающие одинаковое число (например, "1"), представляют группу символов четырехмерного повернутого созвездия. Число, показанное каждой ячейкой, указывает номер группы у соответствующей группы. Также каждая ячейка указывает компонент созвездия у одного измерения. Показанные ниже "Символы созвездия" на фиг. 3 являются состоянием, где выравниваются шесть групп символов четырехмерного повернутого созвездия. Показанные ниже "Комплексные символы" на фиг. 3 являются двенадцатью комплексными символами, которые получаются путем перекомпоновки шести групп символов четырехмерного повернутого созвездия, показанных ниже в "Символах созвездия" на фиг. 3. Отметим, что фиг. 3 показывает три вида "Комплексных символов" в качестве примеров. Во время фактической передачи пара из двух компонентов созвездия, которые являются вертикально выровненными "Комплексными символами" ниже (результат перекомпоновки), модулируется и передается в виде одного комплексного символа. Перемежитель/преобразователь 250 символов выполняет перемежение символов над комплексными символами, введенными из преобразователя 240 комплексных символов, и после этого отображает комплексные символы в разные временные слоты, частоты, антенны передатчика или их сочетания. Здесь перемежение символов может быть блочным перемежением или сверточным перемежением. Цепи модуляции с 260-1 по 260-М предоставляются в однозначном соответствии с антеннами передатчика с 270-1 по 270-М. Каждая из цепей модуляции с 260-1 по 260-М вставляет пилотные сигналы для оценки коэффициентов замирания в соответствующие входные данные от перемежителя/преобразователя 250 символов, а также выполняет различную обработку, например преобразование во временную область, цифро-аналоговое (D/A) преобразование, фильтрацию передачи и ортогональную модуляцию над соответствующими входными данными. Затем каждая из цепей модуляции с 260-1 по 260-М передает сигнал передачи через соответствующую антенну из антенн передатчика с 270-1 по 270 М. Сторона приемника. На стороне приемника должны быть выполнены строго обратные этапы к этапам, выполненным устройством передачи. Фиг. 4 показывает блок-схему устройства приема, соответствующего устройству передачи, чья блок-схема показана на фиг. 2. Устройство приема состоит из антенн приемника с 410-1 по 410-М, цепей демодуляции с 420-1 по 420-М, обратного преобразователя/деперемежителя 430 символов, обратного преобразователя 440 комплексных символов, обратного преобразователя 450 повернутого созвездия, битового деперемежителя 460 и декодера 470 FEC. Цепи демодуляции с 420-1 по 420-М предоставляются в однозначном соответствии с антеннами приемника с 410-1 по 410-М. Каждая из цепей демодуляции с 420-1 по 420-М выполняет обработку, например аналого-цифровое преобразование, фильтрацию приема и ортогональную демодуляцию над сигналом, переданным устройством передачи из фиг. 2 и принятым соответствующей одной из антенн приемника с 410-1 по 410-М. Затем цепи демодуляции с 420-1 по 420-М оценивают (i) значения амплитуды(коэффициенты замирания) в характеристиках канала с использованием пилотных сигналов и (ii) дисперсию шума, и выводят оцененные значения амплитуды и дисперсию шума вместе с принятым сигналом со скорректированной фазой. Обратный преобразователь/деперемежитель 430 символов выполняет обратную обработку к обработке, выполненной перемежителем/преобразователем 230 символов в устройстве передачи, над входными данными от цепей демодуляции с 420-1 по 420-М. Обратный преобразователь 440 комплексных символов выполняет обратную обработку к обработке, выполненной преобразователем 240 комплексных символов в устройстве передачи, над входными данными от обратного преобразователя/деперемежителя 430 символов. Посредством этой обработки можно получить символы N-мерного повернутого созвездия. Обратный преобразователь 450 повернутого созвездия выполняет обработку по обратному отображению над символами N-мерного повернутого созвездия и выводит результат принятия решения по каждому биту, включенному в N-мерное повернутое созвездие. Битовый деперемежитель 460 выполняет обратную обработку к обработке, выполненной битовым перемежителем 220 в устройстве передачи, над входными данными от обратного преобразователя 450 повернутого созвездия. Декодер 470 FEC выполняет декодирование с FEC над входными данными от битового деперемежителя 460. Ниже приводятся дополнительные объяснения касаемо обратного преобразователя 450 повернутого созвездия. Обратный преобразователь 450 повернутого созвездия может выполнять обработку по обратному отображению символов N-мерного повернутого созвездия двумя следующими способами (i) и (ii):(i) сначала устранить поворот созвездия, затем извлечь биты отдельно для каждого измерения;(ii) декодировать биты всех измерений за один этап. Хотя первое решение (вышеупомянутое (i является самым простым, его производительность субоптимальна и даже хуже для повернутых созвездий, чем для неповернутых созвездий. Благодаря его простоте, это решение может использоваться в некоторых недорогих устройствах приема. Хотя второе решение (вышеупомянутое (ii сложнее, оно предлагает гораздо большую производительность в показателях BER при заданном SNR. В дальнейшем второе решение будет описываться подробнее. Как и в случае устройства передачи, предпочтительный вариант осуществления устройства приема включает в себя декодер 470 FEC после обратного преобразователя 450 повернутого созвездия с необязательным битовым деперемежителем 460 между ними, как показано на фиг. 4. Точнее говоря, обратный преобразователь 450 повернутого созвездия, который выполняет обратное отображение повернутого созвездия, принимает N-мерные векторы символов (y1, , yN) и предполагаемые векторы коэффициентов замирания (h1, , hN) и извлекает данные NB битов (b1, , bNB) из каждого символа, как показано на фиг. 5. Когда используется декодирование с FEC, обработка по обратному отображению символовN-мерного повернутого созвездия больше не может выполняться способом жесткого решения, потому что производительность исправления ошибок была бы субоптимальной. Вместо этого должны использоваться "мягкие биты" либо в виде вероятностей, либо в виде логарифмических отношений правдоподобия (LLR). Представление LLR является предпочтительным, потому что умножения вероятностей можно удобно выразить в виде сумм. Путем определения, LLR бита bk показано в следующем выражении 12. Отметим, что в выражении 12 и являются априорными вероятностями того, что bk=0 и bk=1 передавались, когда принимается вектор символа. В соответствии с известной теорией LLR бита bk созвездия имеет точное выражение, показанное в следующем выражении 13. Отметим, что в выражении 13 k является индексом бита, является вектором принятого символа, является диагональной матрицей, имеющей ассоциированные (оцененные) коэффициенты замирания в качестве элементов на главной диагонали, является вектором точки созвездия, является нормой в квадрате и является дисперсией шума. Для N-мерного созвездия норма в квадрате представляет евклидово расстояние в квадрате от векто, принятого символа до вектора символа ослабленного созвездия в N-мерном пространстве. ра Норма в квадрате может выражаться следующим выражением 14. Каждый бит bk делит созвездие на два разбиения равного размера, Sk0 и Sk1, соответствующие тем точкам, для которых bk равен 0 и 1 соответственно. Примеры показаны на фиг. 6 А и 6 В для классического созвездия 16-QAM с кодированием Грея. Фиг. 6 А показывает кодирование созвездия, а фиг. 6B показывает два разбиения для каждого бита bk. Точное выражение для LLR (вышеприведенное выражение 13) сложно вычислить из-за показательных функций, делений и логарифма. На практике выполняется аппроксимация, показанная в следующем выражении 15, называемая max-log, которая вносит незначительные ошибки.[Выражение 15] Используя вышеприведенное выражение 15, вышеупомянутое выражение 13 приводит к гораздо более простому выражению для LLR, которое показано в следующем выражении 16. Для каждого вектора принятого символа нужно вычислить расстояния до всех 2BN точек созвездия и определяется соответствующий минимум для каждого разбиения. Фиг. 7 показывает предпочтительную аппаратную реализацию обратного преобразователя LLR(один пример обратного преобразователя 450 повернутого созвездия, показанного на фиг. 4) для повернутого созвездия 16-QAM (N=2, В=2). Обратный преобразователь LLR состоит из счетчика 710, преобразователя 720 повернутого созвездия, вычислителя 730 квадрата евклидова расстояния, минимизаторов с 740-1 по 740-4 и сумматоров с 750-1 по 750-4. Для каждого вектора принятого символа счетчик 710 многократно формирует все 24=16 точек созвездия и выводит четыре бита b1, b2, b3 и b4, указывающие точки созвездия, в преобразователь 720 повернутого созвездия. Преобразователь 720 повернутого созвездия выбирает точку двумерного повернутого созвездия из справочной таблицы, в качестве индексов используя значения счетчика, предоставленные счетчиком 710,и выводит два компонента s1 и s2 созвездия, полученные посредством этого выбора, в вычислитель 730 квадрата евклидова расстояния. Вычислитель 730 квадрата евклидова расстояния вычисляет евклидовы расстояния в квадрате (см. фиг. 8). Для каждого бита минимизаторы с 740-1 по 740-4 поддерживают соответствующие минимальные евклидовы расстояния в квадрате для двух разбиений (см. фиг. 9). Два разбиения созвездия для каждого бита указываются просто соответствующим битом счетчика 710. Каждый из сумматоров с 750-1 по 750-4 вычитает выход mini (соответствующий биту 1) из выходаmin0 (соответствующего биту 0), причем min1 и min0 предоставляются в каждом из минимизаторов с 740-1 по 740-4. После этого сумматоры с 750-1 по 750-4 выводят результаты вычитания в виде L(b1) поL(b4) соответственно. Фиг. 8 - принципиальная схема вычислителя квадрата евклидова расстояния, который вычисляетN-мерное евклидово расстояние в квадрате. Отметим, что структура схемы вычислителя 730 квадрата евклидова расстояния изменена от схемы, показанной на фиг. 8, чтобы удовлетворять N=2. Вычислитель квадрата евклидова расстояния состоит из умножителей с 810-1 по 810-N, сумматоров с 820-1 по 820-N, умножителей с 830-1 по 830-N, сумматора 840 и умножителя 850. Умножители с 810-1 по 810-N умножают h1 по hN на s1 по sN соответственно. Сумматоры с 820-1 по 820-N вычитают h1S1 по hNsN из y1 по yN соответственно. Умножители с 830-1 по 830-N умножают(y1-h1s1) по (yN-hNsN) на (y1-h1s1) по (yN-hNsN) соответственно. Сумматор 840 складывает выходные сигналы умножителей с 830-1 по 830-N. Умножитель 850 умножает выходной сигнал сумматора 840 на Выходным сигналом умножителя 850 является N-мерное евклидово расстояние в квадрате. Фиг. 9 - принципиальная схема минимизаторов с 740-1 по 740-4, которые вычисляют минимальные евклидовы расстояния в квадрате для каждого бита. Ввод 1-битного поднабора (или разбиения) указывает текущее положение. Каждый из минимизаторов с 740-1 по 740-4 состоит из компаратора 910, селектора 920, инвертора 930, D-триггеров 940-0 и 940-1 и селектора 950. Нижеследующее описывает операции, которые нужно выполнить в ситуации фиг. 9, когда значение поднабора (значение, введенное из счетчика 710) равно "0". Среди выхода D-триггера 940-0 и выхода D-триггера 940-1 селектор 950 выбирает и выводит первый. Компаратор 910 сравнивает цифровой вход (А), который указывает евклидово расстояние в квадрате, вычисленное вычислителем 730 квадрата евклидова расстояния, с выходом (В) селектора 950. В случае, где В меньше А, компаратор 910 выводит "0". В этом случае из цифрового входа и выхода селектора 950 селектор 92 0 выбирает и выводит последний на основе "0", принятого от компаратора 910. С другой стороны, в случае, где А меньше В, компаратор 910 выводит "1". В этом случае из цифрового входа и выхода селектора 950 селектор 920 выбирает и выводит первый на основе "1", принятой от компаратора 910. Отметим, что в случае, где А равно В, такой же результат будет получен независимо от того, выбирает ли селектор 920 цифровой вход или выход селектора 950. Соответственно, в этом случае компаратор 910 может выводить любое из "0" и "1". Инвертор 930 инвертирует значение "0" поднабора. Таким образом, "1" подается на клемму запускаD-триггера 940-0. Когда D-триггер 940-0 запущен, он защелкивает выход селектора 920. Между тем "0" подается на клемму запуска D-триггера 940-1. Когда D-триггер 940-1 не запущен, он не защелкивает выход селектора 920. Нижеследующее описывает операции, которые нужно выполнить в ситуации фиг. 9, когда значение поднабора равно "1". Среди выхода D-триггера 940-0 и выхода D-триггера 940-1 селектор 950 выбирает и выводит последний. Компаратор 910 сравнивает цифровой вход (А) с выходом (В) из селектора 950. В случае, где В меньше А, компаратор 910 выводит "0". В этом случае из цифрового входа и выхода селектора 950 селектор 920 выбирает и выводит последний на основе "0", принятого от компаратора 910. С другой стороны, в случае, где А меньше В, компаратор 910 выводит "1". В этом случае из цифрового входа и выхода селектора 950 селектор 920 выбирает и выводит первый на основе "1", принятой от компаратора 910. Отметим, что в случае, где А равно В, такой же результат будет получен независимо от того, выбирает ли селектор 920 цифровой вход или выход селектора 950. Соответственно, в этом случае компаратор 910 может выводить любое из "0" и "1"."1" подается на клемму запуска D-триггера 940-1. Когда D-триггер 940-1 запущен, он защелкивает выход селектора 920. Между тем инвертор 930 инвертирует значение "1" поднабора. Таким образом, "0" подается на клемму запуска D-триггера 940-0. Когда D-триггер 940-0 не запущен, он не защелкивает выход селектора 920. Значительного улучшения в производительности устройства приема можно достичь, используя итеративное декодирование. Как показано на фиг. 10, устройство приема, сконфигурированное для использования такого итеративного декодирования, состоит из обратного преобразователя 1010 повернутого созвездия, битового деперемежителя 1020, декодера 1030 FEC, сумматора 1040 и битового перемежителя 1050. Здесь обратный преобразователь 1010 повернутого созвездия и декодер 1030 FEC подключаются в петле. Обратный преобразователь 1010 повернутого созвездия выполняет обработку по обратному отображению над символами N-мерного повернутого созвездия и выводит L (см. фиг. 11). Битовый деперемежитель 1020 выполняет обратную обработку к обработке, выполненной битовым перемежителем 220 в устройстве передачи, над входными данными от обратного преобразователя 1010 повернутого созвездия. Декодер 1030 FEC выполняет декодирование с FEC над входными данными от битового деперемежителя 1020. Сумматор 1040 вычитает входные данные от декодера 1030 FEC из выхода декодера 1030 FEC. Битовый перемежитель 1050 выполняет такую же обработку, что и обработка, выполненная битовым пере-7 024628 межителем 220 в устройстве передачи, над выходом сумматора 1040, а затем выводит LE. LE, также называемая внешней информацией, передается по обратной связи обратному преобразователю 1010 повернутого созвездия, чтобы помочь обработке по обратному отображению, выполняемой обратным преобразователем 1010 повернутого созвездия, т.е. обработке по обратному отображению символов N-мерного повернутого созвездия. В этом случае важно, что декодирование с FEC создает "мягкие" биты, например,в виде LLR. Как известно в литературе, формула для вычисления LLR для бита bk имеет вид следующего выражения 17. В выражении 17 представляет K=NB битов, ассоциированных с каждой точкой созвездия, а Xk0 представляют два разбиения созвездия, ассоциированные с битом k, причем каждая точка созвездия и представляет отображающую функцию созвездия. Например, Х 30 и Х 31 показаны в следующем выражении 18. Фиг. 11 показывает пример структуры обратного преобразователя 1010 повернутого созвездия для итеративного декодирования. Отметим, что обратный преобразователь 1010 повернутого созвездия для итеративного декодирования аналогичен обратному преобразователю повернутого созвездия для неитеративного декодирования. Ниже элементам, которые являются такими же, как описаны выше, назначаются одинаковые номера ссылок, и их подробное описание пропускается. Обратный преобразователь 1010 повернутого созвездия состоит из счетчика 710, преобразователя 720 повернутого созвездия, вычислителя 730 квадрата евклидова расстояния, минимизаторов с 740-1 по 740-4, сумматоров с 750-1 по 750-4, операторов логического И с 1110-1 по 1110-4, сумматора 1120, сумматоров с 1130-1 по 1130-4 и сумматоров с 1140-1 по 1140-4. Операторы логического И с 1110-1 по 1110-4 выполняют операции логического И над выходными данными битового перемежителя 1050, а именно с LE(b1) no LE(b4), и выходными данными счетчика 710,а именно с b1 по b4. Сумматор 1120 складывает выходные данные операторов логического И с 1110-1 по 1110-4. Каждый из сумматоров с 1130-1 по 1130-4 вычитает из выхода сумматора 1120 выход соответствующего из операторов логического И с 1110-1 по 1110-4. Каждый из сумматоров с 1140-1 по 1140-4 вычитает из выхода вычислителя 730 квадрата евклидова расстояния выход соответствующего из сумматоров с 1130-1 по 1130-4. Затем каждый из сумматоров с 1140-1 по 1140-4 выводит значение, полученное посредством вычитания, на цифровой вход соответствующего одного из минимизаторов с 740-1 по 740-4. Список источников Непатентная литература. 1. K. Boulle и J.С. Belfiore. "Modulation Scheme Designed for the Rayleigh Fading Channel". Представлено на CISS 1992. 2. B.D. Jelicic и S. Roy. "Design of Trellis Coded QAM for Flat Fading and AWGN Channels". IEEETransactions on Information Theory, том 48, март 2002 г. Сущность изобретения Техническая проблема Как описано выше, хотя внесен широкий диапазон предложений касаемо матриц вращения для вращения созвездия, предложения, которые сделаны до настоящего времени, не предоставляют скольнибудь эффективного способа формирования многомерного повернутого созвездия (многомерной матрицы вращения) для цифровой модуляции с высокой степенью модуляционного разнесения относительно различных размеров созвездий.NPL 2 представляет подход, который использует вращение Гивенса. Проблема у этого подхода в том, что количество параметров для формирования оптимального многомерного повернутого созвездия увеличивается пропорционально квадрату количества измерений в созвездии.NPL 3 представляет два подхода. Первый подход использует каноническое вложение. В соответствии с этим подходом, способ формирования многомерной матрицы вращения однозначно определяется на основе количества измерений и не содержит параметра, дающего возможность оптимизации для разных размеров созвездий. Поэтому проблема у этого подхода в том, что он не предоставляет возможности максимизации эффекта модуляционного разнесения для различных размеров созвездий. Второй подход, представленный NPL 3, формирует многомерную матрицу вращения, имеющую большее количество измерений, с использованием многоуровневого разложения, где двумерные и трехмерные матрицы вращения располагаются уровнями. Проблема у этого подхода в том, что алгебраические соотношения между многоуровневыми матрицами вращения становятся сложнее, когда увеличивается количество измерений, приводя к сложной оптимизации. Цель настоящего изобретения - предоставить эффективный способ формирования многомерного повернутого созвездия (многомерной матрицы вращения) для цифровой передачи с высокой степенью модуляционного разнесения относительно различных размеров созвездий. Также цель настоящего изобретения - предоставить устройство передачи и способ передачи для передачи данных на основе многомерного повернутого созвездия, полученного с использованием вышеупомянутого способа, и устройство приема и способ приема для приема данных на основе многомерного повернутого созвездия, полученного с использованием вышеупомянутого способа. Решение проблемы Устройство передачи согласно настоящему изобретению передает блок данных по множеству каналов передачи. Устройство передачи содержит: модулятор, функционирующий с возможностью выбора одной из множества точек созвездия в соответствии с блоком данных, который нужно передать, причем каждая из множества точек созвездия имеет множество компонентов; и передатчик, функционирующий с возможностью передачи каждого компонента выбранной точки созвездия по разному одному из множества каналов передачи, где (i) множество точек созвездия задается их положениями в N-мерном пространстве, причем положения получаются путем применения ортогонального преобразования к поднабору который является N-мерной целочисленной решеткой, (ii) N кратно четырем и (iii) ортогональное преобразование имеет представление в виде матрицы NN, причем абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Полезные результаты изобретения Вышеприведенное устройство передачи предоставляет возможность эффективного формирования многомерного повернутого созвездия (многомерной матрицы вращения) для цифровой передачи с высокой степенью модуляционного разнесения относительно различных размеров созвездий. Благодаря многомерному повернутому созвездию, полученному с использованием сформированной многомерной матрицы вращения, вышеприведенное устройство передачи также дает возможность передачи данных, которая обеспечивает эффект модуляционного разнесения высокой степени. Краткое описание чертежей Фиг. 1 А иллюстрирует примерное созвездие на плоскости и эффект замирания. Фиг. 1 В иллюстрирует примерное созвездие на плоскости, которое получено путем вращения созвездия из фиг. 1 А, и эффект замирания. Фиг. 2 показывает блок-схему традиционного устройства передачи. Фиг. 3 показывает схематическое изображение, иллюстрирующее отображение символов созвездия в комплексные символы. Фиг. 4 показывает блок-схему традиционного устройства приема. Фиг. 5 - иллюстрация входных и выходных данных обратного преобразователя повернутого созвездия. Фиг. 6 А показывает пример традиционного созвездия 16-QAM с кодированием Грея. Фиг. 6 В иллюстрирует два разбиения для каждого бита созвездия из фиг. 6 А. Фиг. 7 показывает примерную аппаратную реализацию обратного преобразователя с LLR для повернутого созвездия 16-QAM. Фиг. 8 показывает примерную аппаратную реализацию для вычислителя квадрата евклидова расстояния, который вычисляет N-мерное евклидово расстояние в квадрате. Фиг. 9 показывает примерную аппаратную реализацию для минимизатора, который вычисляет минимальные евклидовы расстояния в квадрате. Фиг. 10 показывает блок-схему схемы, которая выполняет итеративное декодирование. Фиг. 11 показывает примерную аппаратную реализацию обратного преобразователя повернутого созвездия для итеративного декодирования. Фиг. 12 показывает блок-схему устройства передачи в соответствии с вариантом осуществления настоящего изобретения. Фиг. 13 показывает блок-схему устройства приема в соответствии с вариантом осуществления настоящего изобретения. Фиг. 14 показывает блок-схема обратного преобразователя повернутого созвездия, показанного на фиг. 13. Описание вариантов осуществления Настоящее изобретение предоставляет первое устройство передачи для передачи блока данных по множеству каналов передачи, причем первое устройство передачи содержит: модулятор, функционирующий с возможностью выбора одной из множества точек созвездия в соответствии с блоком данных,который нужно передать, причем каждая из множества точек созвездия имеет множество компонентов; и передатчик, функционирующий с возможностью передачи каждого компонента выбранной точки созвездия по разному одному из множества каналов передачи, где (i) множество точек созвездия задается их положениями в N-мерном пространстве, причем положения получаются путем применения ортогонального преобразования к поднабору который является N-мерной целочисленной решеткой, (ii) N кратно четырем и (iii) ортогональное преобразование имеет представление в виде матрицы NN, причем абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Настоящее изобретение также предоставляет первый способ передачи для передачи блока данных по множеству каналов передачи, причем первый способ передачи содержит этапы: выбора одной из множества точек созвездия в соответствии с блоком данных, который нужно передать, причем каждая из множества точек созвездия имеет множество компонентов; и передачи каждого компонента выбранной точки созвездия по разному одному из множества каналов передачи, где (i) множество точек созвездия задается их положениями в N-мерном пространстве, причем положения получаются путем применения ортогонального преобразования к поднабору который является N-мерной целочисленной решеткой, (ii) N кратно четырем и (iii) ортогональное преобразование имеет представление в виде матрицыNN, причем абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Вышеприведенные устройство передачи и способ передачи предоставляют возможность эффективного формирования многомерного повернутого созвездия (многомерной матрицы вращения) для цифровой передачи с высокой степенью модуляционного разнесения относительно различных размеров созвездий. Благодаря многомерному повернутому созвездию, полученному с использованием сформированной многомерной матрицы вращения, вышеприведенные устройство передачи и способ передачи также дают возможность передачи данных, которая обеспечивает эффект модуляционного разнесения высокой степени. Настоящее изобретение также предоставляет второе устройство передачи и второй способ передачи, которые являются первым устройством передачи и вторым устройством передачи соответственно,где вместо представления в виде матрицы NN ортогональное преобразование имеет представление в виде матрицы, полученное путем перестановки строк и/или столбцов в представлении в виде матрицыNN. Вышеприведенная структура дает такой же эффект, как и эффект, созданный представлением в виде матрицы NN, причем абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Настоящее изобретение также предоставляет третье устройство передачи, которое является первым устройством передачи, дополнительно содержащим преобразователь, функционирующий с возможностью отображения каждого компонента выбранной точки созвездия в соответствующий один из множества каналов передачи, по которым нужно передать упомянутый компонент, так, чтобы замирание каждого из множества каналов передачи не коррелировало с замиранием любого другого из множества каналов передачи. Настоящее изобретение также предоставляет третий способ передачи, который является первым способом передачи, дополнительно содержащим этап отображения каждого компонента выбранной точки созвездия в соответствующий один из множества каналов передачи, по которым нужно передать упомянутый компонент, так, чтобы замирание каждого из множества каналов передачи не коррелировало с замиранием любого другого из множества каналов передачи. Вышеприведенная структура может оптимизировать производительность передачи даже при наличии замирания. Настоящее изобретение также предоставляет четвертое устройство передачи, которое является первым устройством передачи, в котором передатчик приспособлен для передачи каждого компонента выбранной точки созвездия по разному одному из множества временных слотов, частот, антенн передатчика или их сочетаний. Настоящее изобретение также предоставляет пятое устройство передачи и четвертый способ передачи, которые являются первым устройством передачи и первым способом передачи соответственно,причем множество каналов передачи содержит множество разных несущих в схеме мультиплексирования с ортогональным частотным разделением. Настоящее изобретение также предоставляет шестое устройство передачи и пятый способ передачи,которые являются первым устройством передачи и первым способом передачи соответственно, причем множество каналов передачи содержит множество разных символов в схеме мультиплексирования с ортогональным частотным разделением. Настоящее изобретение также предоставляет первое устройство приема для приема блока данных по множеству каналов передачи, причем первое устройство приема содержит: приемник, функционирующий с возможностью приема множества сигналов компонентов по множеству каналов передачи; и демодулятор, функционирующий с возможностью выбора одной из множества точек созвездия в соответствии с множеством принятых сигналов компонентов, причем (i) множество точек созвездия задается их положениями в N-мерном пространстве, причем положения получаются путем применения ортогонального преобразования к поднабору который является N-мерной целочисленной решеткой,(ii) N кратно четырем и (iii) ортогональное преобразование имеет представление в виде матрицы NN,причем абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Настоящее изобретение также предоставляет первый способ приема для приема блока данных по множеству каналов передачи, причем первый способ приема содержит этапы: приема множества сигналов компонентов по множеству каналов передачи; и выбора одной из множества точек созвездия в соответствии с множеством принятых сигналов компонентов, причем (i) множество точек созвездия задается их положениями в N-мерном пространстве, причем положения получаются путем применения ортогонального преобразования к поднабору который является N-мерной целочисленной решеткой,(ii) N кратно четырем и (iii) ортогональное преобразование имеет представление в виде матрицы NN,причем абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Вышеприведенные устройство приема и способ приема предоставляют возможность эффективного формирования многомерного повернутого созвездия (многомерной матрицы вращения) для цифровой передачи с высокой степенью модуляционного разнесения относительно различных размеров созвездий. Благодаря многомерному повернутому созвездию, полученному с использованием сформированной многомерной матрицы вращения, вышеприведенные устройство приема и способ приема также дают возможность приема данных, который обеспечивает эффект модуляционного разнесения высокой степени. Настоящее изобретение также предоставляет второе устройство приема и второй способ приема,которые являются первым устройством приема и первым способом приема соответственно, где вместо представления в виде матрицы NN ортогональное преобразование имеет представление в виде матрицы, полученное путем перестановки строк и/или столбцов в представлении в виде матрицы NN. Вышеприведенная структура дает такой же эффект, как и эффект, созданный представлением в виде матрицы NN, причем абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Настоящее изобретение также предоставляет третье устройство приема и третий способ приема, которые являются первым устройством приема и первым способом приема, соответственно, причем множество каналов передачи содержит множество разных несущих в схеме мультиплексирования с ортогональным частотным разделением. Настоящее изобретение также предоставляет четвертое устройство приема и четвертый способ приема, которые являются первым устройством приема и первым способом приема соответственно, причем множество каналов передачи содержит множество разных символов в схеме мультиплексирования с ортогональным частотным разделением. Настоящее изобретение также предоставляет первый способ формирования для формирования многомерного созвездия для схемы цифровой модуляции в системе передачи данных, причем первый способ формирования содержит этапы: приема множества векторов в многомерном векторном пространстве; и получения точек созвездия в многомерном созвездии путем применения ортогонального преобразования к множеству принятых векторов, причем (i) ортогональное преобразование приспособлено для увеличения минимального количества разных значений в компонентах любых двух различных точек многомерного созвездия относительно минимального количества разных значений в компонентах любых двух различных принятых векторов и (ii) ортогональное преобразование имеет представление в виде матрицыNN, причем N кратно четырем, абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Вышеприведенный способ формирования предоставляет возможность эффективного формирования многомерного повернутого созвездия (многомерной матрицы вращения) для цифровой передачи с высокой степенью модуляционного разнесения относительно различных размеров созвездий. Настоящее изобретение также предоставляет второй способ формирования для формирования многомерного созвездия, причем второй способ формирования является первым способом формирования, в котором вместо представления в виде матрицы NN ортогональное преобразование имеет представление в виде матрицы, полученное путем перестановки строк и/или столбцов в представлении в виде матрицыNN. Вышеприведенная структура дает такой же эффект, как и эффект, созданный представлением в виде матрицы NN, причем абсолютные значения всех элементов на главной диагонали равны первому значению, а абсолютные значения всех элементов не на главной диагонали равны ненулевому второму значению. Настоящее изобретение также предоставляет третий способ формирования для формирования многомерного созвездия, причем третий способ формирования является первым способом формирования,дополнительно содержащим этапы: выбора коэффициента r вращения в виде вещественного числа между 0 и 1; вычисления первого значения, а, путем оценивания выражения и определения ортогонального преобразования путем выбора знакового значения si,j для каждого элемента (i, j) в в виде матрицы представлении так, чтобы представление в виде матрицы являлось ортогональным. С помощью вышеприведенной структуры можно легко определить ортогональное преобразование. Настоящее изобретение также предоставляет четвертый способ формирования для формирования многомерного созвездия, причем четвертый способ формирования является третьим способом формирования, в котором выбранный коэффициент r вращения максимизирует минимальное количество разных значений в компонентах любых двух различных точек многомерного созвездия. Вышеприведенная структура предоставляет возможность достижения высокой степени модуляционного разнесения и к тому же повышенной устойчивости при наличии замирания, сохраняя при этом спектральную эффективность. Настоящее изобретение также предоставляет пятый способ формирования для формирования многомерного созвездия, причем пятый способ формирования является первым способом формирования, в котором множество принятых векторов представляет поднабор который является N-мерной целочисленной решеткой. Вышеприведенная структура полезна в непосредственной числовой реализации. Нижеследующее описывает вариант осуществления настоящего изобретения со ссылкой на чертежи. Сначала приводится описание предложенных многомерных матриц вращения. Многомерные матрицы вращения обладают одним независимым параметром и структурой, которая является регулярной, насколько это возможно. Параметр может конфигурироваться, чтобы минимизировать вероятность ошибки для различных размеров созвездий. В частности, два следующих условия (i) и(ii) накладываются на многомерную матрицу вращения, применяемую для получения многомерного повернутого созвездия.(i) Каждый выход должен иметь доминирующий вход.(ii) Оставшиеся входы должны иметь равные веса. Вышеприведенные условия (i) и (ii) выполняются, если многомерная матрица вращения имеет форму, показанную в следующем Выражении 19 (для N=4), или в более общем смысле, форму, показанную в следующем выражении 20. Отметим, что многомерная матрица вращения, показанная в выражении 20,является матрицей NN. Здесь а и b обозначают вещественные параметры, причем каждое знаковое значение si,j удовлетворяет Отметим, что значения параметров а и b, которые выполняют вышеприведенные условия (i) и (ii),удовлетворяют реляционному выражению аb0. Очевидно, таких же преимуществ можно достичь путем перестановки строк и/или столбцов многомерной матрицы вращения, показанной в вышеприведенном выражении 20. Поэтому матрица, показанная в выражении 20, может использоваться в качестве многомерной матрицы вращения. В качестве альтернативы также можно использовать матрицу, полученную путем перестановки строк и/или столбцов матрицы, показанной в выражении 20, в качестве многомерной матрицы вращения. Матрица, показанная в Выражении 20, и матрица, полученная путем перестановки строк и/или столбцов матрицы, показанной в выражении 20, обладают следующими признаками: (i) каждая строка содержит элемент, имеющий вещественный параметр a; (ii) каждый столбец содержит элемент, имеющий вещественный параметр а; и(iii) оставшиеся элементы в каждом строке/столбце имеют вещественный параметр b. Нижеследующее описывает нормализацию многомерной матрицы вращения, показанной в вышеприведенном выражении 20. Отметим, что аналогичная нормализация может выполняться над матрицей(многомерной матрицей вращения), полученной путем перестановки строк и/или столбцов матрицы, показанной в выражении 20. Условие нормализации устанавливает отношение, показанное в следующем выражении 21, между параметрами а и b. Поэтому многомерная матрица вращения имеет только один независимый параметр. В следующем выражении 22 задаем "коэффициент вращения" r между 0 и 1. Преимущество использования "коэффициента вращения" r в том, что диапазон всегда составляет от 0 до 1 независимо от количества измерений. Оптимальное значение для "коэффициента вращения" r зависит от размера созвездия, т.е. количества измерений N и количества битов В на каждое измерение для квадратных/кубических созвездий. Отметим, что значение r, удовлетворяющее вышеупомянутым условиям (i) и (ii), больше 0 и меньше 1. Многомерная матрица вращения для вращения многомерного созвездия может быть нормализованной или ненормализованной. Единственный открытый вопрос состоит в том, какие значения должна принимать знаковая матрица Знаковая матрица задается следующим выражением 24. Необходимое условие, которое, тем не менее, не является достаточным, состоит в том, что знаковая матрица должна быть ортогональной вплоть до масштабного коэффициента. Такие матрицы известны в литературе в качестве матриц Адамара. Поскольку а и b в многомерной матрице вращения отличаются, должно быть наложено дополнительное условие, показанное в следующем выражении 25.[Выражение 25] Это условие обеспечивает, что любое произведение аb компенсируется соответствующим произведением bа. Если все элементы на главной диагонали имеют одинаковый знак, и каждая пара элементов, которые симметричны относительно главной диагонали, имеет противоположные знаки, то это условие выполняется. Примеры таких особенно предпочтительных знаковых матриц для четырехмерного и 8D Нужно отметить, что матрицы Адамара возможны только для размеров, которые являются кратными четырем. Поэтому многомерные матрицы вращения существуют только для количеств измерений,которые кратны четырем. Таким образом, количество измерений созвездия в соответствии с настоящим изобретением предпочтительно кратно четырем (например, 4, 8, 12 и 16). зафиксирована, результирующую многомерную матрицу вращеКак только знаковая матрица ния можно оптимизировать для определенного размера созвездия, т.е. количества битов или точек созвездия на измерение, путем выполнения следующих этапов: выбора "коэффициента вращения" r соответственно; и вычисления параметров а и b путем подстановки выбранного "коэффициента вращения" r в вышеприведенное выражение 23. С этой целью может применяться любой подходящий алгоритм оптимизации. В качестве цели оптимизации может применяться минимальное количество разных значений в компонентах любых двух различных точек многомерного повернутого созвездия. Также могут быть использованы другие цели оптимизации. В соответствии с предпочтительным вариантом осуществления настоящего изобретения, задается функция стоимости, которая учитывает минимальные абсолютные разности между соответствующими компонентами любых двух различных точек многомерного повернутого созвездия. Пример такой функции стоимости вычисляет минимум по всем N абсолютным разностям между соответствующими компонентами двух точек многомерного повернутого созвездия и суммирует эти минимальные значения или их квадраты по всем парам точек многомерного повернутого созвездия. Многомерное повернутое созвездие уже может быть полезным, если минимальное количество разных значений в компонентах любых двух различных точек многомерного повернутого созвездия больше минимального количества в отношении многомерного неповернутого созвездия. Также многомерное повернутое созвездие уже может быть полезным, если минимальная абсолютная разность двух соответствующих компонентов любых двух различных точек многомерного повернутого созвездия больше таковой в отношении многомерного неповернутого созвездия. В предпочтительном варианте осуществления настоящего изобретения весь процесс передачи,включая канал передачи и декодер, моделируется для определения частоты появления ошибочных битов."Коэффициент вращения" r тогда можно адаптировать, чтобы минимизировать определенную частоту появления ошибочных битов. Поэтому настоящее изобретение предоставляет возможность формирования многомерного повернутого созвездия, которое может использоваться для модулирования и передачи данных по множеству(под)каналов с замираниями или временных слотов с оптимальной спектральной эффективностью. С этой целью устанавливается традиционное гиперкубическое созвездие с нужным количеством измеренийN и нужным количеством битов на измерение (т.е. количеством точек созвездия на направление), например, путем выбора подходящего поднабора Здесь является набором всех точек N-мерного пространства, имеющих целочисленные координаты. Это гиперкубическое созвездие может быть, например, обобщением традиционного регулярного созвездия QAM до N измерений. Однако могут использоваться и другие исходные созвездия, например, обобщения кругового созвездия до N измерений и т.д. Как только устанавливается исходное созвездие, оно может быть подвергнуто вращению путем применения заданной выше многомерной матрицы вращения к каждой из точек исходного созвездия,чтобы получить повернутое множество точек созвездия, т.е. многомерное повернутое созвездие. Многомерное повернутое созвездие может быть более подходящим, чем исходное созвездие, в показателях обеспечиваемой степени модуляционного разнесения, в зависимости от конкретного выбора "коэффициента вращения" r. "Коэффициент вращения" r, а вслед за ним и повернутое созвездие могут меняться, как описано выше, чтобы получить созвездие, которое обеспечивает максимальное модуляционное разнесение или, по меньшей мере, определенную минимальную степень модуляционного разнесения, которая требуется конкретным применением. Настоящее изобретение также предоставляет способ и устройство для эффективной передачи и приема данных по множеству (под)каналов с замираниями или временных слотов на основе схемы модуляции, которая применяет многомерное повернутое созвездие, которое получено по вышеописанному способу. Изобретенный способ или устройство могут либо выполнить вышеописанный способ, чтобы получить нужное многомерное повернутое созвездие, либо использовать набор предварительно определенных и предварительно записанных точек созвездия в многомерном повернутом созвездии, которые вычислены с использованием вышеописанного способа. В последнем случае изобретенный способ или устройство могут обращаться к средству хранения, в котором хранится информация, указывающая положения, по меньшей мере, некоторых точек созвездия. Другой аспект настоящего изобретения касается разделения и отображения N измерений N-мерного повернутого созвездия, чтобы они испытывали независимое замирание во время передачи. Это ключевой аспект, необходимый для достижения предполагаемой производительности разнесения. Как правило, этого можно достичь путем передачи каждого из N компонентов точки созвездия вN-мерном повернутом созвездии по разному одному из множества каналов передачи при условии, что замирание каждого из этих каналов передачи не коррелирует с замиранием любого другого из каналов передачи. Здесь фраза "разный один из множества каналов передачи" может относиться к разному одному из множества временных слотов, частот, антенн передатчика или их сочетаний. Применительно к мультиплексированию с ортогональным частотным разделением (OFDM) фраза "разный один из множества каналов передачи" может относиться, в частности, к разному одному из множества активных несущих, символов OFDM или их сочетаний. Применительно к системе с одиночной несущей фраза "разный один из множества каналов передачи" может относиться, в частности, к разному одному из множества символов или временных слотов. Возможна дополнительная обработка сигналов перед передачей. Критический аспект состоит в том,что замирание, испытываемое каждым из N измерений, должно отличаться или в идеале не коррелировать с замиранием, испытываемым любым другим из N измерений. Распределение N измерений на разные временные слоты, частоты и антенны передатчика может достигаться, например, посредством подходящего перемежения и отображения. Другой аспект настоящего изобретения касается отображения N вещественных измерений вN-мерном повернутом созвездии в комплексные символы для передачи. Поскольку замирание синфазного компонента и квадратурного компонента заданного канала обычно идентично, комплексный символ может не состоять из двух разных компонентов одной и той же точки созвездия. Вместо этого N компонентов точки созвездия должны отображаться в разные комплексные символы, чтобы обеспечить желаемое разнесение. Комплексные символы, сформированные таким образом, затем распределяются традиционным способом по доступным временным слотам, частотам и/или антеннам, например посредством перемежения и отображения, чтобы замирание, испытываемое каждым из N измерений, не коррелировало с замиранием, испытываемым любым другим из N измерений. Нижеследующее описывает примерный алгоритм способа для формирования многомерного созвездия для схемы цифровой модуляции при передаче данных. Этот алгоритм выполняется, например, компьютерной системой. Каждый из следующих этапов исполняется центральным процессором (CPU). Этап 1. Принимается множество векторов в N-мерном векторном пространстве. Отметим, например, что множество принятых векторов представляет поднабор который является N-мерной целочисленной решеткой. Этап 2. Определяются знаковые значения si,j в знаковой матрице, показанной в вышеприведенном выражении 24, так, чтобы N-мерная матрица вращения показанная в вышеприведенном выражении 20, являлась ортогональной. Этап 3. "Коэффициент вращения" г выбирается в виде вещественного числа между 0 и 1. Следует отметить, что "коэффициент вращения" r выбирается, например, так, что он максимизирует минимальное количество разных значений в компонентах любых двух различных точек многомерного созвездия. Однако настоящее изобретение этим не ограничивается. В качестве альтернативы "коэффициент вращения"r может выбираться так, что он увеличивает минимальное количество разных значений в компонентах любых двух различных точек N-мерного повернутого созвездия относительно минимального количества разных значений в компонентах любых двух различных векторов, принятых на этапе 1. Этап 4. Значения параметров а и b вычисляются путем подстановки значения "коэффициента вращения" r, который выбран на этапе 3, в вышеприведенное выражение 23. Этап 5. N-мерная матрица вращения определяется из вышеприведенного Выражения 20 с использованием (i) знаковой матрицы имеющей знаковые значения si,j, определенные на этапе 2, и(ii) значений параметров а и b, вычисленных на этапе 4. Этап 6. Точка созвездия в N-мерном повернутом созвездии получается путем применения N-мерной матрицы вращения определенной на этапе 5, к множеству векторов многомерного векторного пространства, которые приняты на этапе 1. Фиг. 12 - блок-схема устройства передачи в соответствии с вариантом осуществления настоящего изобретения, которое аналогично показанному на фиг. 2. Элементам, которые являются такими же, как описаны выше, назначаются одинаковые номера ссылок, и их подробное объяснение опускается. Устройство передачи из фиг. 12 отличается от такового из фиг. 2 тем, что обратный преобразователь 230 повернутого созвездия заменяется обратным преобразователем 1230 повернутого созвездия. Обратный преобразователь 1230 повернутого созвездия выполняет обработку на основе N-мерного повернутого созвездия, которое содержит множество точек созвездия, заданных их положениями вN-мерном пространстве, причем положения получаются путем применения либо N-мерной матрицы вращения, показанной в вышеприведенном выражении 20, либо N-мерной матрицы вращения, полученной путем перестановки строк и/или столбцов N-мерной матрицы вращения, показанной в вышеприведенном выражении 20, к поднабору который является N-мерной целочисленной решеткой. Точнее говоря, эта обработка состоит в отображении выходного сигнала битового перемежителя 220 в повернутое созвездие. Фиг. 13 - блок-схема устройства приема в соответствии с вариантом осуществления настоящего изобретения, которое аналогично показанному на фиг. 4. Элементам, которые являются такими же, как описаны выше, назначаются одинаковые номера ссылок, и их подробное объяснение опускается. Устройство приема из фиг. 13 отличается от такового из фиг. 4 тем, что обратный преобразователь 450 повернутого созвездия заменяется обратным преобразователем 1350 повернутого созвездия. Обратный преобразователь 1350 повернутого созвездия выполняет обработку на основе N-мерного повернутого созвездия, которое содержит множество точек созвездия, заданных их положениями в N-мерном пространстве, причем положения получаются путем применения либо N-мерной матрицы вращения, показанной в вышеприведенном выражении 20, либо N-мерной матрицы вращения, полученной путем перестановки строк и/или столбцов N-мерной матрицы вращения, показанной в вышеприведенном выражении 20, к поднабору который является N-мерной целочисленной решеткой. Фиг. 14 показывает примерную аппаратную реализацию для обратного преобразователя 1350 повернутого созвездия из фиг. 13 для повернутого созвездия 16-QAM (N=2, В=2). Обратный преобразователь 1350 повернутого созвездия из фиг. 13 включает в себя преобразователь 1420 повернутого созвездия вместо преобразователя 720 повернутого созвездия, показанного на фиг. 7. Преобразователь 1420 повернутого созвездия отображает выходы с b1 по b4 от счетчика 710 в N-мерное повернутое созвездие, которое содержит множество точек созвездия, заданных их положениями в N-мерном пространстве, причем положения получаются путем применения либо N-мерной матрицы вращения, показанной в вышеприведенном выражении 20, либо N-мерной матрицы вращения, полученной путем перестановки строк и/или столбцов N-мерной матрицы вращения, показанной в вышеприведенном выражении 20, к поднабору который является N-мерной целочисленной решеткой. Затем преобразователь 1420 повернутого созвездия выводит результирующие компоненты созвездия с s1 no s4 в вычислитель 730 квадрата евклидова расстояния. Следует отметить, что структуры устройства передачи и устройства приема не ограничиваются описанными выше. Например, устройство приема может иметь любую из структур, показанных на фиг. 10 и 11. В этом случае обратный преобразователь 1010 или 720 повернутого созвездия выполняет обработку на основе N-мерного повернутого созвездия, которое содержит множество точек созвездия, заданных их положениями в N-мерном пространстве, причем положения получаются путем применения либоN-мерной матрицы вращения, показанной в вышеприведенном выражении 20, либо N-мерной матрицы вращения, полученной путем перестановки строк и/или столбцов N-мерной матрицы вращения, показанной в вышеприведенном выражении 20, к поднабору который является N-мерной целочисленной решеткой. Настоящее изобретение относится к цифровой передаче данных и предоставляет эффективный способ для формирования многомерных созвездий для цифровой модуляции данных с высокой степенью модуляционного разнесения, способ для передачи и приема данных на основе таких созвездий и соответствующее устройство. Это достигается путем рассмотрения только многомерных матриц вращения со всеми элементами на диагонали, имеющими одинаковое первое абсолютное значение, и всеми остальными элементами, имеющими одинаковое второе абсолютное значение. Таким образом, можно формировать многомерные матрицы вращения, имеющие один независимый параметр и структуру, которая регулярна, насколько это возможно. Независимый параметр может конфигурироваться, чтобы минимизировать вероятность ошибки для различных размеров созвездий. Промышленная применимость Настоящее изобретение применимо к устройству связи,цию/демодуляцию с использованием созвездия. Список условных обозначений: 210 - кодер FEC,220 - битовый перемежитель,1230 - преобразователь повернутого созвездия,240 - преобразователь комплексных символов,250 - перемежитель/преобразователь символов,260-1 - 260-М - цепь модуляции,270-1 - 270-М - антенна передатчика,410-1 - 410-М - антенна приемника,420-1 - 420-М - цепь демодуляции,430 - обратный преобразователь/деперемежитель символов,440 - обратный преобразователь комплексных символов,1350 - обратный преобразователь повернутого созвездия,460 - битовый деперемежитель,470 - декодер FEC. модуля ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Устройство передачи для передачи блока данных по множеству каналов передачи, причем устройство передачи содержит модулятор, функционирующий с возможностью формирования одной из множества точек созвездия, являющегося результатом поворота исходного созвездия, в соответствии с блоком данных, который подлежит передаче, причем каждая из множества точек упомянутого созвездия, являющегося результатом поворота созвездия, имеет N компонентов, причем каждая из множества точек исходного созвездия имеет N компонентов, причем поворот созвездия представлен матрицей R размером NN; и передатчик, функционирующий с возможностью передачи каждого компонента сформированной точки созвездия по разному одному из множества каналов передачи,причем N кратно четырем, где а и b обозначают вещественные параметры,каждое знаковое значение si,j удовлетворяет 2. Устройство приема для приема блока данных по множеству каналов передачи, причем устройство приема содержит приемник, функционирующий с возможностью приема N сигналов компонентов по множеству каналов передачи; и демодулятор, функционирующий с возможностью демодуляции принятых N сигналов компонентов на основе созвездия, являющегося результатом поворота исходного созвездия, причем каждая из множества точек упомянутого созвездия, являющегося результатом поворота созвездия, имеет N компонентов,причем каждая из множества точек исходного созвездия имеет N компонентов, причем поворот созвездия представлен матрицей R размером NN,причем N кратно четырем, где а и b обозначают вещественные параметры,каждое знаковое значение si,j удовлетворяет 3. Способ передачи для передачи блока данных по множеству каналов передачи, причем способ передачи содержит этапы, на которых формируют одну из множества точек созвездия, являющегося результатом поворота исходного со- 18024628 звездия, в соответствии с блоком данных, который подлежит передаче, причем каждая из множества точек упомянутого созвездия, являющегося результатом поворота созвездия, имеет N компонентов, причем каждая из множества точек исходного созвездия имеет N компонентов, причем поворот созвездия представлен матрицей R размером NN; и передают каждый компонент сформированной точки созвездия по разному одному из множества каналов передачи,причем N кратно четырем, где а и b обозначают вещественные параметры,каждое знаковое значение si,j, удовлетворяет 4. Способ приема для приема блока данных по множеству каналов передачи, причем способ приема содержит этапы, на которых принимают N сигналов компонентов по множеству каналов передачи; демодулируют принятые N сигналов компонентов на основе созвездия, являющегося результатом поворота исходного созвездия, причем каждая из множества точек упомянутого созвездия, являющегося результатом поворота созвездия, имеет N компонентов, причем каждая из множества точек исходного созвездия имеет N компонентов, причем поворот созвездия представлен матрицей R размером NN,причем N кратно четырем, где а и b обозначают вещественные параметры,каждое знаковое значение si,j удовлетворяет 5. Способ цифровой модуляции в системе передачи данных, причем способ содержит этапы, на которых принимают множество векторов в N-мерном векторном пространстве, связанном с исходным созвездием; и получают множество точек созвездия N-мерного созвездия, являющегося результатом поворота созвездия, в соответствии с множеством принятых векторов, причем поворот созвездия приспособлен для увеличения минимального количества разных значений в компонентах любых двух различных точек Nмерного созвездия относительно минимального количества разных значений в компонентах любых двух различных принятых векторов, причем поворот созвездия представлен матрицей R размером NN, где а и b обозначают вещественные параметры,каждое знаковое значение si,j удовлетворяет
МПК / Метки
МПК: H04B 7/02
Метки: устройство, приема, передачи, многомерных, способ, созвездий, формирования
Код ссылки
<a href="https://eas.patents.su/25-24628-ustrojjstvo-peredachi-ustrojjstvo-priema-sposob-peredachi-sposob-priema-i-sposob-dlya-formirovaniya-mnogomernyh-sozvezdijj.html" rel="bookmark" title="База патентов Евразийского Союза">Устройство передачи, устройство приема, способ передачи, способ приема и способ для формирования многомерных созвездий</a>
Предыдущий патент: Производные криптофицина и его конъюгаты, их получение и применение в терапии
Следующий патент: Моноклональные антитела, связывающие b7h6, и их применение
Случайный патент: Датчик