Усовершенствования извлечения углеводородов из коллектора углеводородов

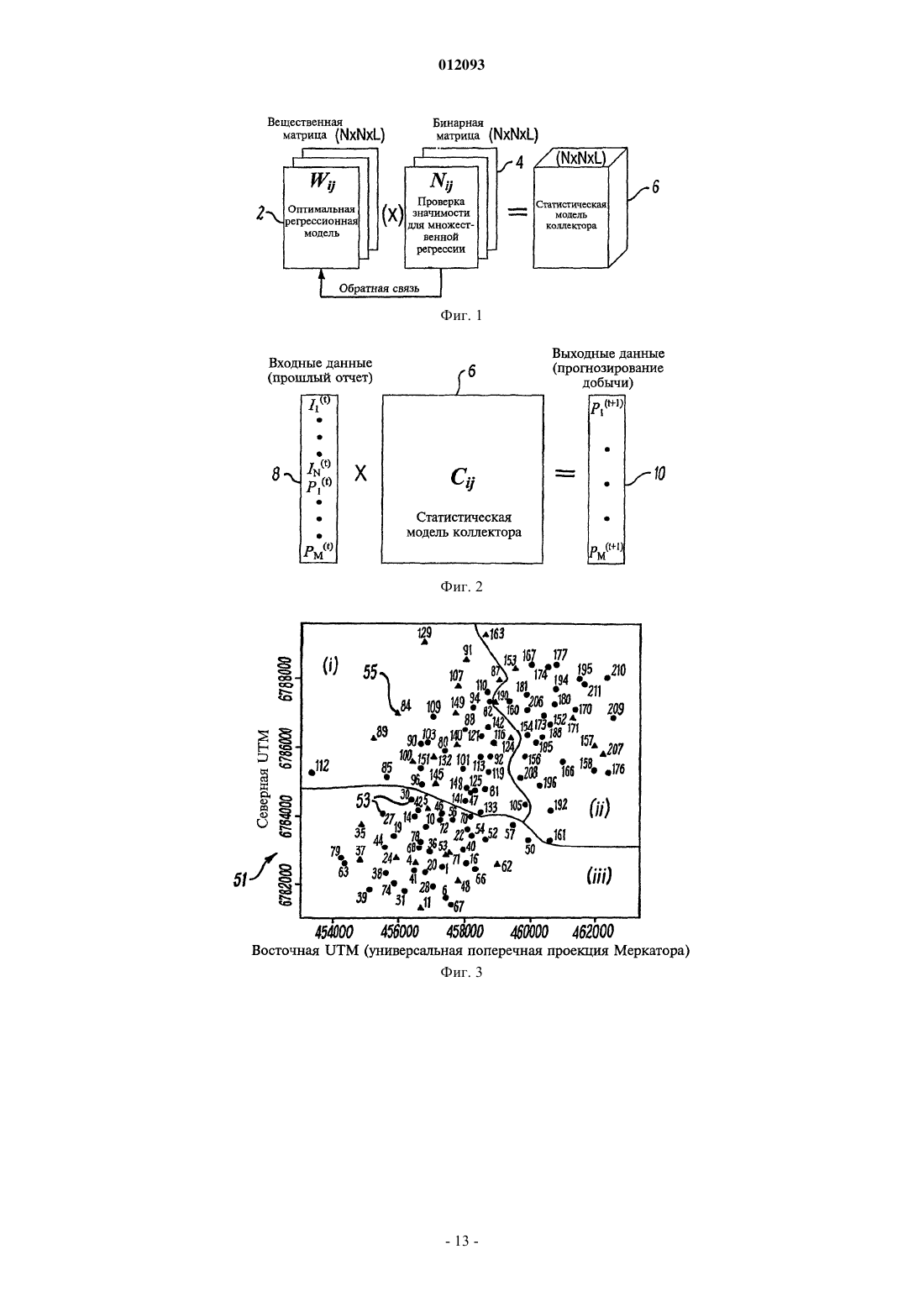
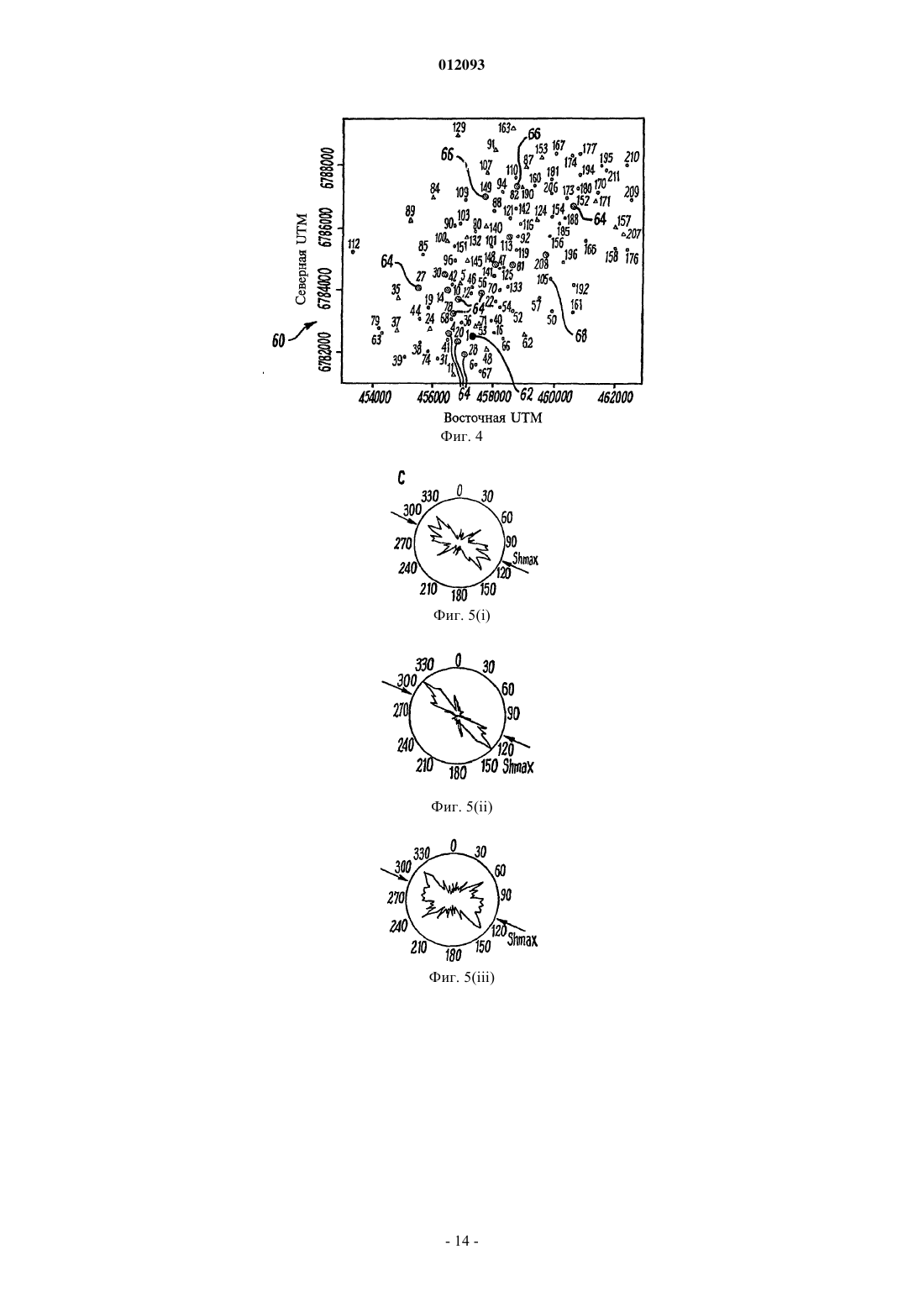
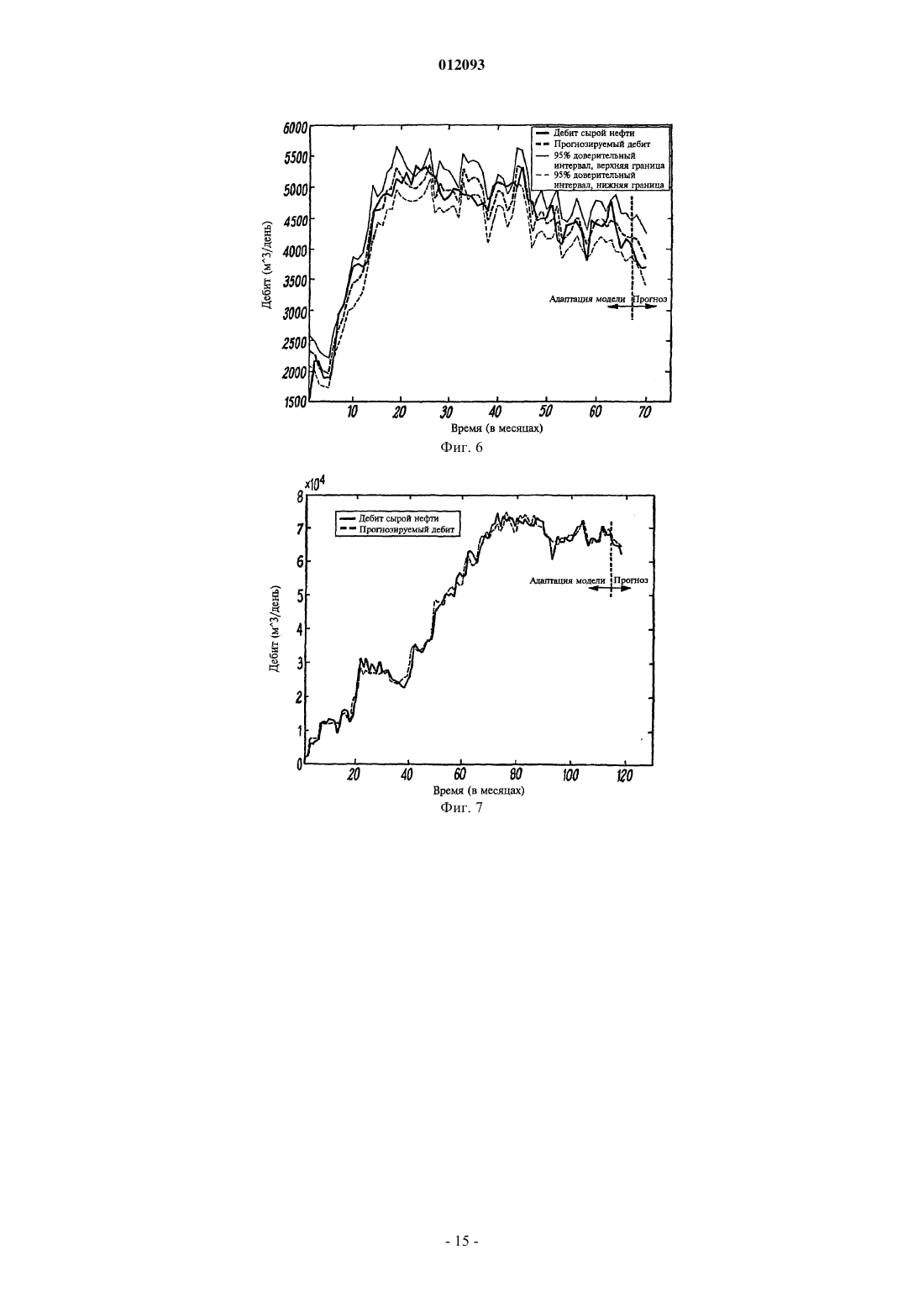
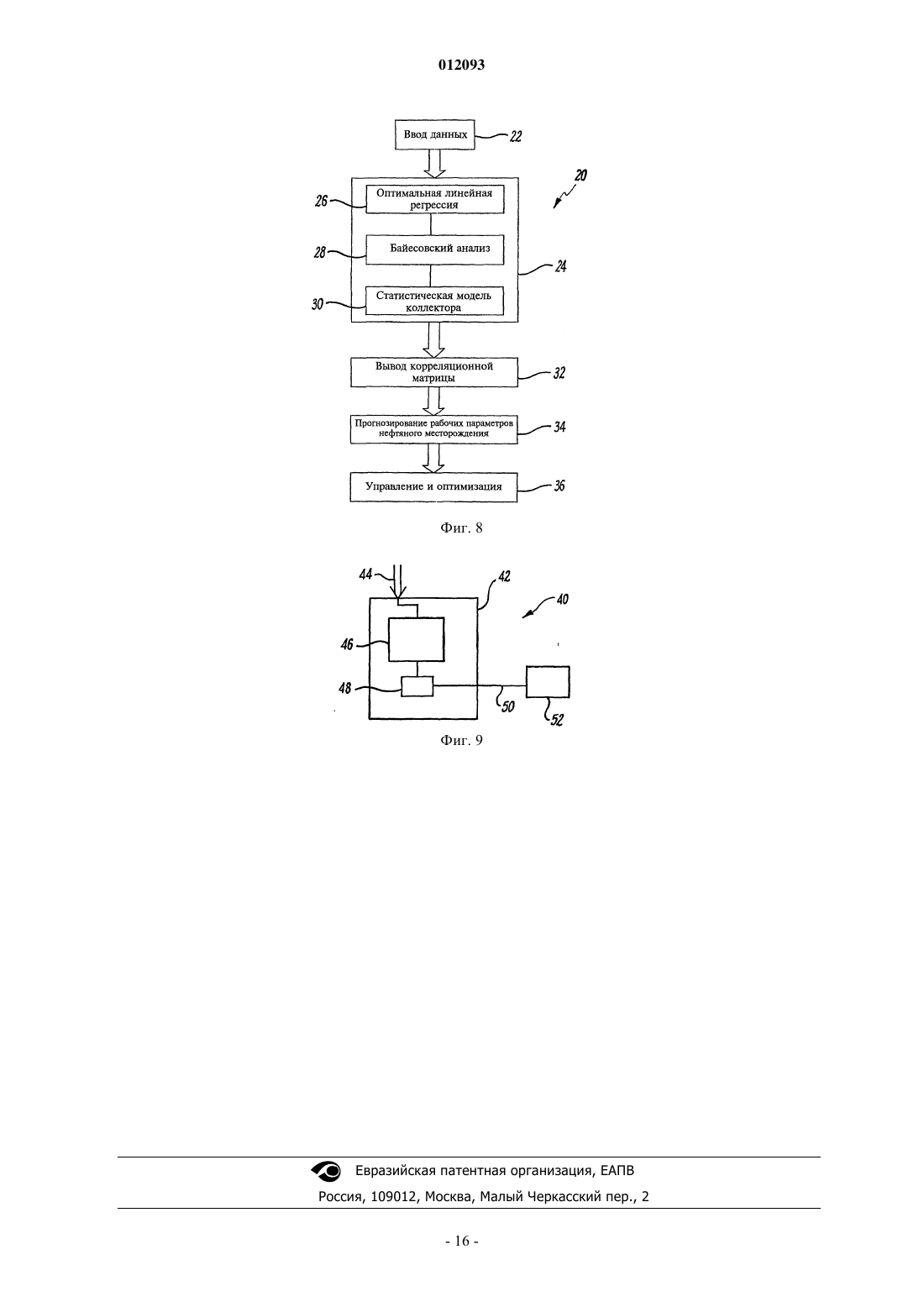
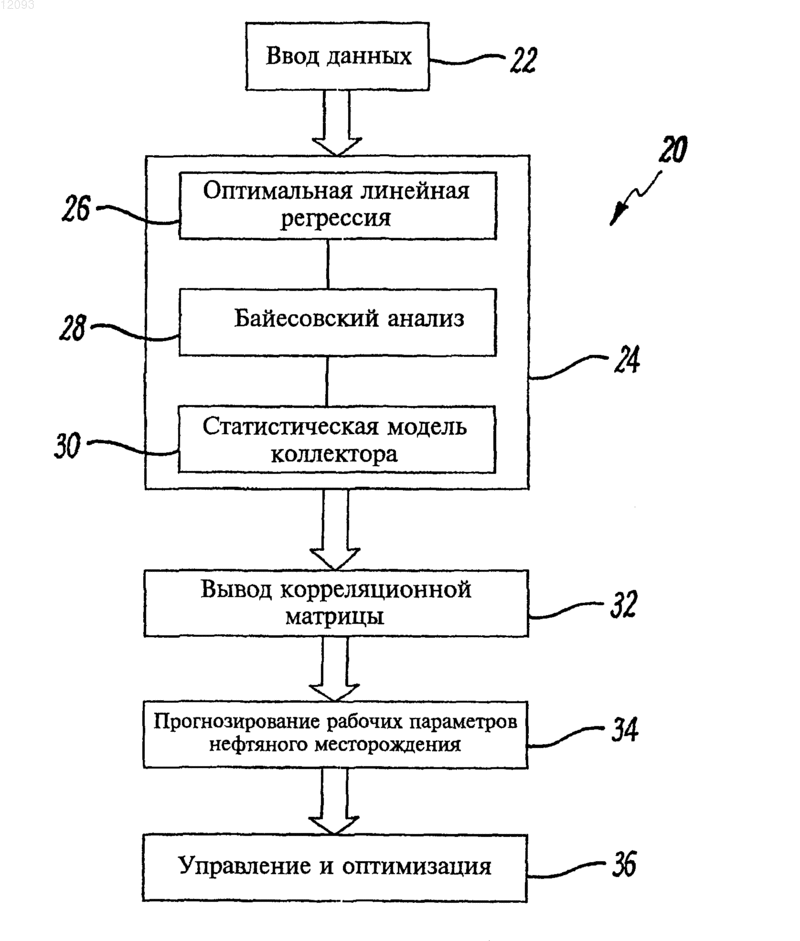
012093 Настоящее изобретение относится к усовершенствованиям извлечения жидких нефтепродуктов и углеводородного газа из коллектора углеводородов. В частности, это изобретение относится к системам,содержащим системы управления, которые включают в себя моделирование коллектора углеводородов на основе данных по нагнетанию и добыче на нефтяных месторождениях и позволяют контролировать,прогнозировать и управлять добычей углеводородов и обслуживанием коллекторов. Коллекторы углеводородных флюидов, которые входят в структуру нефтяных месторождений, типично содержат подземную массу породы с пористостью, подходящей для хранения и передачи текучей среды. Нагнетательные и добывающие скважины пробуривают в коллектор, что позволяет извлечь углеводородные флюиды. Основной целью нагнетательной скважины является поддержание давления в коллекторе посредством нагнетания заданного количества текучей среды для создания избыточного давления, которое позволит легко извлечь углеводородные флюиды. Коллектор может иметь 50 пробуренных нагнетательных и добывающих скважин, каждая из которых обеспечивает ввод в коллектор или вывод из него. Желательно обеспечить максимальный контроль над нагнетательными и добывающими скважинами. Однако большое количество вводов/выводов коллектора, наряду со сложной геологией и геофизикой коллектора, делает чрезвычайно сложным предсказание реакции как коллектора, так и нагнетательных и добывающих скважин, на изменения в коллекторе. Известно, что отдельные добывающие скважины на нефтяных промыслах под заводнением могут обладать очень высокой чувствительностью к отдельным нагнетательным скважинам, т.е. нагнетание текучей среды из отдельной нагнетательной скважины может иметь непропорционально большое влияние на добычу. Кроме того, очень высокая чувствительность к отдельным нагнетательным скважинам напрямую связана с напряженным состоянием и имеет долгосрочную природу. В некоторых случаях в месторождениях могут наблюдаться картины чувствительности, схожие с картинами сбросообразования. Наиболее подходящее объяснение этих эффектов заключается в том, что системы сбросов и разломов и поле напряжений, действующее на них, приводят к критическому, или близкому к нему, состоянию, когда возмущения пороупругого напряжения, вызванные колебаниями в расходах текучей среды, оказывают влияние на их индивидуальные проницаемости. Сложные конфигурации, высокая чувствительность к возмущениям и долгосрочные корреляции характерны для многих физических систем в критической точке. Отдельные системы со многими степенями свободы, далекие от равновесия, и которые постоянно получают энергию, рассеивающуюся затем по системе, могут самостоятельно организовываться в точке критичности без внешней настройки соответствующих параметров. Возмущения в их естественном состоянии, вызываемые процессами, имеющими место при разработке месторождения, будут тогда также подобны процессу самоорганизации. Способ, использующий корреляционные связи для прогнозирования функционирования сложных нелинейных систем, использовался в банковском деле и сфере страхования в течение многих лет. Например, прогнозирование частоты наводнений или ураганов в следующем году на основании основных показателей погоды текущего года учитывалось при определении страховых взносов. Эти статистические или "эвристические" модели всегда применяются со ссылками на дополнительную физическую модель или предыдущий опыт, и редко используются сами по себе для прогнозирования тенденций в будущем. В качестве альтернативы, в управлении нефтяными месторождениями ранее использовались значительно более простые методы корреляции, первоначально как средство определения, имеет ли локальное поле напряжений большое влияние на производительность нефтяного месторождения. Heffer и другие(1997) для проверки направленности корреляционных связей относительно поля максимального горизонтального напряжения использовали метод ранговой корреляции Спирмена. Результаты показали сильную ориентацию направления корреляции сейсмических данных во всех восьми проведенных экспериментах. Главное преимущество метода ранговой корреляции Спирмена перед традиционной регрессией на основе метода наименьших квадратов состоит в том, что он может установить, существует ли корреляция. Его главный недостаток заключается в том, что он не может затем расставить точные статистические границы погрешности параметров и, следовательно, не может быть использован для непосредственного получения количественной статистической модели коллектора, которая может применяться для прогнозирования реакции коллектора на заданные изменения в стратегии нагнетания или добычи. Поэтому желательно разрабатывать новые способы для установления точных прогнозирующих корреляций между дебитами нагнетательных и добывающих пар скважин. Это дает новую информацию,которая может или подтвердить физическую модель коллектора, или указать области, где компоненты реакции коллектора не улавливаются. Целью настоящего изобретения является прогнозирование работы нефтяного месторождения с временными рамками в несколько месяцев для того, чтобы, например, содействовать планированию стратегий нагнетания текучей среды или оптимизировать графики планового ремонта и обслуживания. Еще одной целью настоящего изобретения является предоставление устройства и способа для усовершенствования извлечения углеводородов на основании анализа данных дебита добывающих и нагне-1 012093 тательных скважин нефтяного месторождения. В соответствии с первым аспектом настоящего изобретения представлена вычислительная система для моделирования поведения коллектора углеводородов с тем, чтобы управлять потоком текучей среды внутри коллектора; эта вычислительная система содержит модуль анализа, анализирующий данные добычи нефтяного месторождения посредством выполнения программных команд, которые содержат оптимальную регрессионную модель, представляющую нагнетательные и добывающие скважины, характеристики потока текучей среды которых сильно коррелируют с характеристиками потока текучей среды интересующей скважины; выполняющий программные команды, использующие метод критерия ограниченной информации для определения пар скважин,которые вносят статистически значимую информацию в оптимальную регрессионную модель; выполняющий программные команды, в результате которых получают статистическую модель коллектора,состоящую из произведения оптимальной регрессионной модели и матрицы значимости; и средство управления для регулирования одной или более скважин для управления потоком текучей среды в ответ на реакцию статистической модели коллектора, составленной модулем анализа. Вычислительная система может управлять потоком текучей среды в коллекторе посредством изменения потока в одной или более представляющих интерес скважинах. Предпочтительно средство управления регулирует производительность одной или более скважин. Предпочтительно средство управления регулирует вытеснение или конфигурацию нагнетания в нагнетательной скважине. Предпочтительно средство управления выполнено с возможностью определения положения загущающих скважин. Предпочтительно средство управления выполнено с возможностью автоматического управления одной или более скважинами. Предпочтительно средство управления выполнено с возможностью регулирования нагнетания текучей среды в коллектор. Предпочтительно текучей средой является вода или углекислый газ. Предпочтительно метод ограниченной информации включает метод Бейеса. Предпочтительно матрица значимости является бинарной матрицей значимости. Предпочтительно для создания оптимальной регрессионной модели для нагнетательных и добывающих скважин используется множественная линейная регрессионная модель. Предпочтительно множественная линейная регрессионная модель:(a) определяет модель прогнозируемой среднеквадратической ошибки для заданного временного интервала;(b) минимизирует прогнозируемую среднеквадратичную ошибку для получения формальной множественной линейной регрессионной модели;(c) осуществляет поиск оптимальной регрессионной модели на основании предлагаемой стратегии выбора наилучшей модели, причем данная стратегия заключается в автоматическом прямом переборе вариантов модельного пространства прицельно по всем возможным парам скважин, используя модифицированный байесовский информационный критерий (BIC); и(d) получает оптимальную регрессионную модель, когда (a) R2 превышает заданное значение, в то время как BIC еще возрастает, (b) R2 уменьшается или (с) достигается заданное количество итераций. Предпочтительно временной интервал составляет один месяц. Могут использоваться и другие временные интервалы для нагнетательных и добывающих скважин, включая и нулевой временной интервал. Предпочтительно оптимальная регрессионная модель определяется из массива множественных линейных регрессионных моделей, причем разработана стратегия выбора наилучшей модели в режиме прицельного автоматического перебора вариантов модельного пространства с целью сравнения различных моделей с использованием модифицированного байесовского информационного критерия (BIC). Для небольших коллекторов с малым количеством нагнетательных скважин информационный критерий Акайке (AIC) может оказаться предпочтительней. Предпочтительно модель с наибольшим значением BIC выбирается при одновременно возрастающем коэффициенте детерминации (R2). Предпочтительно полный байесовский анализ применяется к байесовской динамической линейной модели (DLM), основанной на методе Монте-Карло с использованием цепей Маркова (MCMC), причемDLM имеет те же прогнозирующие параметры, что и прогнозирующие параметры, определенные в оптимальной регрессионной модели. Предпочтительно полный байесовский анализ дополнительно содержит:(a) определение байесовской DLM, в которой DLM модель имеет те же прогнозирующие параметры, что и прогнозирующие параметры, определенные в оптимальной регрессии, с соответствующими случайными ошибками, взаимно независимыми и распределенными по нормальному закону с нулевым математическим ожиданием, и конечными дисперсиями;(b) использование допущения априорного распределения для неизвестных параметров для DLM модели, где соответствующие дисперсии имеют распределение хи-квадрат;(c) использование функции правдоподобия неизвестных параметров;(d) вычисление плотностей совместных апостериорных распределений неизвестных параметров;(e) вычисление соответствующих плотностей полного условного распределения каждого параметра в моделях;(f) применение алгоритма выборочного метода Гиббса для непосредственного получения плотностей полного апостериорного распределения неизвестных параметров; и(g) получение матрицы значимости, исходя из плотности апостериорного распределения коэффициента регрессии, причем если плотность апостериорного распределения коэффициента регрессии имеет центр в нуле, то этот коэффициент наиболее вероятно равен нулю, в противном случае этот коэффициент равен единице. Матрица значимости может быть двоичным массивом единиц и нулей. Предпочтительно предлагаемая байесовская DLM относится к модели квадратичного роста, в которой случайные ошибки соответствуют уровню, росту и изменению роста для основного процесса изменения давлений во время t. Предпочтительно предполагается, что случайные ошибки взаимно независимы и распределены по нормальному закону с нулевым математическим ожиданием и конечной дисперсией. Предпочтительно упрощенные DLM модели получают, если обнаруживается, что некоторые компоненты дисперсии равны нулю. Предпочтительно выборочный метод Гиббса и MCMC схема для осуществления моделирования позволяет получить плотности полного условного апостериорного распределения полных неизвестных параметров. Предпочтительно оптимальная регрессионная модель, полученная из множественной линейной регрессионной модели, представляет собой вещественную матрицу. Предпочтительно матрица значимости, полученная из полного байесовского анализа, представляет собой бинарную матрицу. Предпочтительно статистическую модель коллектора получают как произведение вещественной матрицы регрессии и бинарной матрицы значимости. Матрица оптимальной регрессионной модели представляет собой массив вещественных чисел для одного или более различных временных интервалов, а матрица значимости, полученная из байесовского анализа, представляет собой двоичный массив из единиц и нулей для тех же самых пар скважин при тех же самых временных интервалах. Настоящее изобретение предлагает новую стратегию выбора оптимальной модели, которая автоматически осуществляет прицельный перебор вариантов по всем возможным парам скважин, используя модифицированный байесовский информационный критерий (BIC), определяющий значимость, совместно с коэффициентом детерминации (R2) в качестве критерия остановки процесса. Байесовская динамическая линейная модель (DLM) устанавливает соответствующую бинарную матрицу значимости, применяя приближение полного байесовского анализа на основании метода МонтеКарло с использованием цепей Маркова. Полный байесовский анализ уменьшает вероятность случайных корреляций, снижающих прогнозирующую силу. Настоящее изобретение может быть использовано для подтверждения правильности обычной модели коллектора или для прогнозирования с помощью эвристического метода реакции коллектора на плановые мероприятия при разработке месторождения, такие как увеличение расхода при нагнетании, организация "выметания" пласта или остановки для текущего ремонта. Настоящее изобретение может также оценивать вероятность "случайных" корреляций, снижающих прогнозирующую силу, которые являются наиболее серьезной потенциальной проблемой для любой эвристической статистической модели. Применяемые методы способны выявить (и способствовать выяснению основной причины) общую природу корреляций дебита нагнетательной и добывающей пары скважин в зависимости от времени. Настоящее изобретение может использовать множественную линейную регрессионную модель,чтобы установить оптимальную регрессионную модель давлений в скважине на основании данных по добыче на нефтяном месторождении. Затем получают соответствующую бинарную матрицу значимости,применяя приближение полного байесовского анализа к предлагаемой байесовской динамической линейной модели (DLM) с помощью методов Монте-Карло с использованием цепей Маркова (MCMC). Как показано на фиг. 1, статистическая модель 6 коллектора является произведением отдельных элементов оптимальной регрессионной модели 2 (массив вещественных чисел) и матрицы значимости 4 (двоичный массив единиц и нулей), а не стандартным перемножением матриц. Концепция статистической модели коллектора иллюстрируется на фиг. 1. Если статистическая модель коллектора разработана для единичного временного интервала, то она принимает форму двумерной матрицы. Ожидаемая производительность Pj во время t+1 для j-й добывающей скважины прогнозируется из значений прошлого и текущего дебита i-й нагнетательной скважины Ii или добывающей скважины Pi во время t, t-1, t-2,. Фиг. 2 представляет перемножение матриц, которое иллюстрирует этот прогноз для единичного временного интервала L=1, производительности 10 Pj и значений дебита 8.-3 012093 Результаты настоящего изобретения способствуют оптимизации продуктивности углеводородных скважин в интервале нескольких месяцев, например, для ежедневных операций по добыче, в качестве инструкции по управлению расходом отдельных скважин, предоставляя более точные прогнозы производительности на будущее. Дополнительно настоящее изобретение может автоматически обновлять совокупность корреляций расхода между скважинами месторождения и предоставлять, в качестве руководства, совокупность (краткосрочных) оптимальных расходов скважины начальнику производственного участка. Настоящее изобретение дополняет традиционное моделирование коллектора, которое основано на подробном описании коллектора и имитации потока текучей среды. В частности, оно может быть использовано, как возможный способ перебора вариантов, с тем, чтобы определить, когда геомеханические имитации необходимы (чтобы рассчитать долгосрочную корреляцию), а когда достаточно обычного дренирования пласта (поток Дарси). Далее настоящее изобретение будет описано только в качестве примера со ссылкой на сопровождающие фигуры. Фиг. 1 схематически представляет параметры статистической модели коллектора, используемой в вычислительной системе в соответствии с настоящим изобретением. Фиг. 2 представляет соотношение между входными данными, выходными данными и статистической моделью коллектора. Фиг. 3 является картой 51, которая показывает расположение пронумерованных добывающих 53 скважин (кружки) и нагнетательных скважин (треугольники) для типичного нефтяного месторождения. Фиг. 4 является картой, которая показывает расположение скважин, существенно коррелирующих с данной добывающей скважиной нефтяного месторождения. Фиг. 5(i)-(iii) представляют розы-диаграммы распределения ориентации существенно коррелирующих пар скважин для различных зон нефтяного месторождения. Фиг. 6 представляет график временной зависимости дебита на основании настоящего изобретения для прогнозирования дебита одиночной скважины. Фиг. 7 представляет график временной зависимости дебита на основании настоящего изобретения для прогнозирования дебита группы скважин. Фиг. 8 представляет общую схему, в которой вычислительная система настоящего изобретения используется для получения характеристик и управления работой нефтяного месторождения. Фиг. 9 представляет вычислительную систему в соответствии с настоящим изобретением. Используются данные добычи сырой нефти, составленные из ежемесячных средних измерений дебита (как правило, объем в баррелях или м 3 в месяц), получаемые в течение нескольких месяцев. Там, где позволяют данные, возможны более высокие частоты выборки. Значения дебита пропорциональны давлению скважины. Для нагнетательных скважин входные данные представляют собой полный дебит воды и/или газа или другой текучей среды, нагнетаемой в нижние горизонты. Для добывающих скважин эти данные представляют собой полный дебит. Настоящее изобретение используется для общего дебита, но оно также может осуществлять прогноз при нарушении соответствующих пропорций нефти, газа и воды в добывающих скважинах. Не исключено, что для каждой скважины какие-то данные будут пропущены вследствие текущего ремонта, неполной записи данных и/или по другой причине. Кроме того, ряд скважин действуют и в качестве добывающих, и в качестве нагнетательных, т.е. в течение нескольких месяцев они эксплуатируются для добычи, а в течение других месяцев используются для нагнетания воды и/или газа. Для всех последующих вычислений временные ряды для каждой скважины сначала нормируются так, чтобы выборочное среднее значение было 0, а среднеквадратичное отклонение - единицей, что дает возможность непосредственного сравнения. Теперь будет описана математическая основа по меньшей мере одного варианта осуществления вычислительной системы настоящего изобретения. Модель прогнозируемой среднеквадратичной ошибки. Чтобы определить добывающие и нагнетательные скважины, давление которых сильно коррелирует с давлением выбранной интересующей добывающей скважины, предлагаемая модель может быть представлена в форме прогнозируемой среднеквадратичной ошибки где xt-k является вектором нагнетания в выбранных скважинах во время t-k, где k(0) является временным интервалом, и yt-k является вектором добычи в выбранных скважинах во время t-k, включая возможно выбранную добывающую скважину во время t-k, a 1 и 2 являются неизвестными параметрами вектора. В уравнении (1) модель представляет собой двумерную матрицу, но может расширяться, включая несколько временных интервалов k, образуя в результате трехмерный массив (фиг. 1). Эта общая модель-4 012093 может быть модифицирована в соответствии с возможными оптимальными временными интервалами,например, включение добавочных временных интервалов для нагнетательных и добывающих скважин,или уменьшение количества членов, рассматриваемых в (1). Множественная линейная регрессионная модель. Минимизация модели (1) приводит к следующей форме множественной линейной регрессии: Следовательно, решение модели (1) приводит к решению задачи множественной линейной регрессии (2). Когда устанавливается зависимость интересующей величины от подмножества потенциальных прогнозирующих параметров, имеется неопределенность в выборе подмножества из-за множества избыточных и/или посторонних прогнозирующих параметров. В методах выбора модели важную роль играет критерий выбора модели. Байесовский информационный критерий (BIC) является одним из самых распространенных критериев для моделей отбора. BIC основан на байесовском принципе, заключающемся в том, что модель выбирают с наибольшей апостериорной вероятностью, и это лучше действует для большого набора данных, таких как здесь рассматриваются. Приведенный ниже модифицированный BIC критерий пригоден для того, чтобы определить хорошие прогнозирующие параметры. Модифицированный BIC критерий. Модифицированный BIC критерий для сравнения различных моделей представлен в нормированном варианте BIC где k - число оцениваемых параметров и S2R - стандартная остаточная сумма квадратов. Когдаlog[N/(2)]2, то мы получаем AIC (информационный критерий Акайке), а когда log[N/(2)]2, то мы получаем стандартный BIC. С помощью этого практического критерия можно в соответствии с замечанием получить значение BIC, и сравнить модели с различными наборами данных, выбирая модель с наибольшим значением критерия. Стратегия выбора наилучшей модели. Общее количество возможных моделей очень велико. В регрессии с 50 прогнозирующими параметрами имеется 1,12591015 возможных моделей, которые можно рассматривать. Поэтому была разработана стратегия перебора такого большого объема моделей. Предлагаемая стратегия выбора наилучшей модели, называемая прицельным поиском, представляет собой прицельный автоматический перебор вариантов всего пространства моделей по всем возможным парам скважин, используя модифицированныйBIC критерий. Преимуществом такой стратегии является значительное уменьшение времени, необходимого для расчетов. В этой связи, стратегия использует автоматический параллельный перебор вариантов в прямом направлении всех возможных моделей в пространстве моделей, для сравнения различных моделей, используя BIC критерий, определяемый формулой (3), и выбора прогнозирующего параметра с наибольшим значением BIC при одновременно возрастающем коэффициенте детерминации (R2). Это является новой стратегией выбора, что придает идее статистической модели коллектора характер практического предложения для всего нефтяного промысла. Подробная стратегия может быть описана следующим образом. Для всех скважин (нагнетательных, добывающих и оптимальных значений месячных временных интервалов) на каждом шаге выбирается наилучший прогнозирующий параметр, который дает максимальный BIC в (3) при одновременно возрастающем R2. Правилом остановки является (a) R2 превосходит заданное значение, в то время когда BIC еще возрастает, (b) R2 уменьшается или (с) достигается заданное количество итераций. Байесовский анализ DLM. Этот раздел представляет методику байесовского анализа предлагаемой DLM для установления статистической модели коллектора. Предлагаемая байесовская динамическая линейная модель (DLM) относится к динамической линейной модели квадратичного роста, которая имеет те же прогнозирующие параметры, что и прогнозирующие параметры, установленные в оптимальной регрессионной модели. Цель полного байесовского анализа заключается в подтверждении существенных корреляций, наблюдаемых в оптимальной регрессионной модели. Байесовская динамическая линейная модель. Предлагаемая байесовская DLM может быть записана, как для t=1, 2, , N, со случайными ошибками t, t t и t, взаимно независимыми и распределенными по нормальному закону с нулевым математическим ожиданием, и дисперсиями V, V, V и V соответственно. Кроме того, предположим также, что 0, b0 и h0 взаимно независимы и распределены по нормальному закону с нулевым математическим ожиданием и отдельно с дисперсиями V, V и V с определенными ,и . Эта модель относится к динамической линейной модели квадратичного роста, изученной West иHarrison (1997), но с дополнительными членами регрессии в (4) и неизвестными дисперсиями V, V, V и V. Зависимость давления скважины i во время t от прошлых и текущих значений давления некоторых скважин с хорошими прогнозирующими параметрами описывается функцией регрессии xtT и ростом основного процесса t, bt и ht, которые соответствуют уровню, росту и изменению роста с соответствующей погрешностью наблюдения t. Правдоподобие. Правдоподобие вектора наклона,и четырех компонент дисперсии V, V, V и V суть Апостериорное распределение. Мы полагаем, что вектор наклонаи четыре компоненты дисперсии V, V, V и V независимы;распределен по нормальному закону с математическим ожиданием 0 и ковариационной матрицей априорное распределение четырех дисперсий, 11/V, 22/V, 33/V и 44/V имеет распределения хи-квадрат со степенями свободы 1, 2, 3 и 4 соответственно. Плотность совместного апостериорного распределения t, bt и ht вектора наклонов и четырех дисперсий может быть записана, как Вышеупомянутая плотность совместного апостериорного распределения может быть использована,чтобы получить плотности полного условного распределения каждого из параметров, а впоследствии получить плотность апостериорного распределения, используя выборочный метод Гиббса. Согласно алгоритму выборочного метода Гиббса апостериорное распределение неизвестных параметров может быть образовано из полных условных распределений, когда цепь Маркова имеет стационарное распределение.-6 012093 Для реализации алгоритма выборочного метода Гиббса нам необходимы условные апостериорные распределения. Полные условные распределения. На основе этих данных и с учетом всех других неизвестных случайных переменных и параметров модели мы делаем следующие утверждения.A1: 0 распределена по нормальному закону с математическим ожиданием 0, где и дисперсия А 2: для t=1, 2, , N-1 t распределена по нормальному закону с математическим ожиданием t, где и дисперсияA3: N распределена по нормальному закону с математическим ожиданием N, где и дисперсия А 4: b0 распределена по нормальному закону с математическим ожиданием b0, где и дисперсия А 5: для t=1, 2, , N-1 bt распределена по нормальному закону с математическим ожиданием bt, где и дисперсия А 6: bN распределена по нормальному закону с математическим ожиданием bN, где А 7: h0 распределена по нормальному закону с математическим ожиданием h0, где и дисперсия А 8: для t=1, 2, , N-1 ht распределена по нормальному закону с математическим ожиданием ht, где и дисперсия А 9: hN распределена по нормальному закону с математическим ожиданием hN, где и дисперсия А 14: векторраспределен по нормальному закону с математическим ожиданием , где Поскольку все эти полные условные распределения доступны, реализация выборочного метода Гиббса для выборки t, t, ht, вектора наклонов и четырех дисперсий из А 1-А 14 не вызывает затруднений. Две упрощенные модели. Если некоторые из компонент дисперсии равны нулю, то предлагаемая DLM может давать две упрощенные модели.(1) Динамическая линейная модель линейного роста. Если V=0, то все ht нули. Поэтому мы можем получить упрощенную динамическую линейную модель линейного роста и члены регрессии из выражений (4), (5) и (6), которые могут быть представлены в виде Соответствующие плотности полных условных апостериорных распределений могут быть получены из А 1-А 6, А 10-А 12 и А 14 с ht=0 для t=1, 2, , N.(2) Двухступенчатая модель Маркова. Если, кроме того, V=0, то тогда все ht и bt тоже равны нулю. Упрощенная модель представляет собой двухступенчатую модель Маркова (Leonard и Hsu, 1999, с. 233) с наложенными случайными помехами и членами регрессии, приведенными ниже Соответствующие плотности полных условных апостериорных распределений могут быть получены из А 1-А 3, A10, A11 и А 14, с bt=0 для t=1, 2, , N. Матрица значимости. Чтобы получить соответствующую матрицу значимости, может быть выполнен полный байесовский анализ предлагаемой DLM при трех множествах априорных параметров для компонент дисперсии. В качестве априорных параметров выбраны-8 012093 Кроме того, мы задаем ===2. Для вектора наклонамы всегда полагаем тот же самый априорный параметр со средним значением ноль и диагональной ковариантной матрицей со всеми дисперсиями, равными 10. Соответствующие плотности апостериорных распределений устойчивы при испытании трех различных моделей после 50000 итераций. Кроме того, матрица значимости может быть получена по правилу: плотность апостериорного распределения коэффициента наклона, с центром в нуле, наиболее вероятно означает нулевой коэффициент. Если найдено, что прогнозирующий параметр хорошо согласуется с оптимальной регрессионной моделью, а также с полным байесовским анализом DLM, то это показывает, что этот прогнозирующий параметр статистически значимый. Поэтому для матрицы значимости это утверждение основано на тесте матрицы значимости: если прогнозирующий параметр значимый, то Nij=1. В противном случае, утверждение Nij=0. В настоящем изобретении статистическая модель коллектора является произведением оптимальной регрессии и матрицы значимости, как это показано на фиг. 1. Оптимальная регрессионная модель давления скважин является вещественной матрицей, представляющей нагнетательные и добывающие скважины, давление которых существенно коррелирует с давлением данной интересующей добывающей скважины на основании множественной линейной регрессии, используя модифицированный BIC критерий и предлагаемую стратегию выбора наилучшей модели. Соответствующая матрица значимости является бинарной матрицей, которая отображает, является ли прогнозирующий параметр статистически значимым или нет, на основании полного байесовского анализа предлагаемой динамической линейной модели(DLM). Теперь будет описан пример использования настоящего изобретения для характеристики углеводородного коллектора. Этот пример будет моделировать подземную реакцию на изменения во входных или выходных данных добывающей или нагнетательной скважин. Во-первых, минимизируется ошибка прогнозирования между наблюдаемыми расходами yi,t текучей,среды для i-й добывающей скважины для периодов времени t=2, , T и прогнозируемым значением посредством множественной регрессии по вектору xt-k элементов, содержащих дебиты xj,t-k для всех N добывающих и M нагнетательных скважин во время t-k, где k - временной интервал. Решение (29) для всех yi,t представляет собой статистическую модель коллектора- вектор прогнозируемых расходов текучей среды во всех N добывающих скважинах и Rk - матрица параметров регрессии. Для более чем одного временного интервала Rk будет трехмерным массивом с элементами ri,j,k: i=1, , N; j=1, , N+M; k=1, , K. Инверсия для оптимальной статистической модели коллектора выполняется в две стадии. Вопервых, используя модифицированный байесовский информационный критерий (BIC), устанавливаются пары скважин, которые существенно коррелируют при различных временных интервалах. При этом исключаются пары скважин, которые не дают существенного информационного вклада. Практически поиск для данной добывающей скважины останавливается, когда (a) R2 превышает заданное значение, в то время как BIC еще возрастает, (b) R2 уменьшается или (с) достигается заданное количество итераций. Вовторых, используется байесовское динамическое линейное моделирование, чтобы исключить пары, оптимальный коэффициент регрессии которых незначительно отличается от нуля. Вместе эти две стадии определяют бинарную матрицу значимости, Sij, где большинство элементов равны нулю, что дает в результате ограниченную модель. Обычно требуется только 5-25 скважин из 106 скважин подопытного пласта, чтобы достичь R2=0,99 для добывающей скважины. Данные были представлены как ежемесячные средние значения, и рассматривались в качестве временных рядов. Для тех пар скважин, которые определялись как значимые, Sij=1, и оптимальная модель регрессии Rij рассчитывалась, используя (29). Исследуя степень согласия полученных временных рядов, были установлены оптимальные временные интервалы k=0 и k=1 месяц. Такие временные интервалы обнаруживают как прямой (мгновенный) эффект, согласующийся с пороупругим механизмом передачи напряжения при закачивании или откачивании текучей среды, так и эффект, зависящий от времени, порядка одного или нескольких месяцев, последний подобен наблюдаемому при серии толчков после основного землетрясения или вызываемому сейсмичностью. Фиг. 3 является картой 51, которая показывает расположение пронумерованных добывающих 53 скважин (кружки) и нагнетательных 55 скважин (треугольники) нефтяного месторождения, подразделенных на три области, связанные с платформами (i), (ii) и (iii). Фиг. 4 является картой 60, которая показывает расположение значимо коррелирующих скважин-9 012093 нефтяного месторождения. Карта 60 устанавливает интересующую скважину 62, значимо коррелирующие скважины (все скважины 64, отмеченные большими заштрихованными кружками) и другие скважины 68, отмеченные маленькими кружками. Некоторое количество значимо коррелирующих скважин 64 расположены вблизи интересующей скважины 62. Кроме того, также показана корреляция с удаленными на большое расстояние скважинами 66. Фиг. 5 (i)-(iii) являются роза-диаграммами распределения ориентации значимо коррелирующих пар скважин для разных областей относительно направления максимального главного горизонтального напряжения в области. Фиг. 6 и 7 являются графиками временной зависимости дебита единичной скважины (фиг. 6) и множественных скважин (фиг. 7), представляющих фактические данные за прошлый период и прогнозируемую добычу. На обеих фигурах представлен точный прогноз дебита с рассчитанной погрешностью,полученный с использованием настоящего изобретения. Вычислительная система в соответствии с настоящим изобретением выполнена с возможностью управления работой скважин нефтяного месторождения с учетом прогнозируемого эффекта, вызываемого изменениями или возмущениями в скважине в процессе ее эксплуатации. Настоящее изобретение дает возможность использовать новую методологию для действующих нефтяных и газовых месторождений по всему миру. В отличие от других систем, которые зависят от отображения структуры нефтяного месторождения, она использует значения дебита нагнетательных и добывающих скважин. Поскольку на всех углеводородных месторождениях такие данные, в сущности,собираются, то потенциально этот способ имеет почти универсальное применение. Этот метод может быть использован для объяснения функционирования коллектора в прошлом (режим согласования статистических данных), или для прогнозирования реакции коллектора на плановые изменения в стратегии нагнетания, не исключая возможности изменения этих планов, если планируемый сценарий не приводит к оптимальному извлечению нефти и газа из коллектора. Нет необходимости использовать этот способ для замены обычного детерминированного моделирования коллектора, основанного на представляемых и предполагаемых гидравлических свойствах недр. Скорее он может быть использован как дополнительный метод для проверки того, являются ли прогнозы подобного детерминированного метода адекватными, или выделить области, где эта детерминированная модель нуждается в модификации. Главным результатом испытаний является уровень, которого статистическая модель коллектора может достичь при выявлении долгосрочных корреляций, согласующихся с геомеханическими эффектами, и, следовательно, необходимы ли такие вычисления для данного нефтяного месторождения. Настоящее изобретение основано на выявлении сильной направленности потоков месторождения, в особенности, сильной ориентации пар скважин, определенных посредством бинарной матрицы значимости, относительно направления максимального главного напряжения (для смещения при растяжении) или двух ортогональных направлений сброса Кулона (для зарождающегося разрушения при сбросе). Территориальное распределение главных компонент матрицы показывает сильную корреляцию с расположением и ориентацией основных нанесенных на карту сбросов в коллекторах, исследованных до настоящего времени, давая возможность, привлекая систему настоящего изобретения, определять и каналы, и препятствия текучей среде. Фиг. 8 представляет основную схему 20, в которой настоящее изобретение используется для характеристики и управления работой нефтяного месторождения. Данные 22 вводятся в средство анализа 24 настоящего изобретения. Это средство анализа выполняет различные статистические и математические операции с этими данными для того, чтобы сначала выбрать оптимальную регрессионную модель 26, которая представляет нагнетательные и добывающие скважины, чьи характеристики потока текучей среды весьма значительно коррелируют с характеристиками потока текучей среды интересующей скважины. Затем применяется байесовский метод 28 для определения пар скважин, которые в оптимальной регрессионной модели статистически связаны друг с другом. Статистическую модель 30 коллектора получают как произведение матрицы значимости и регрессионной модели. Средство анализа 24 позволит определить стратегии для управления потоком посредством средства управления. Модель 32, выводимая из средства анализа 24, используется для управления 34 нефтяным месторождением. Эффективность управления оптимизируется 36 посредством использования данных, полученных из средства анализа. Фиг. 9 представляет устройство в соответствии с настоящим изобретением. Устройство 40 включает в себя вычислительную систему 42, куда вводятся исходные данные для получения данных по добыче. Модуль 46 анализа содержит набор программных команд, которые анализируют данные о добыче, и управляющее средство, которое предоставляет команды управления для функционирования одной или более скважин в ответ на данные, выходящие из модуля 46 анализа. Команды управления средства 48 управления предоставляют выходные данные 50 для скважины 52. Команды управления могут быть приспособлены для того, чтобы дать возможность прекратить эксплуатацию скважины для ремонта, или они могут являться частью стратегии "выметания", или, например, использоваться для оптимизации добычи.- 10012093 Настоящее изобретение может быть использовано при планировании усиленного, улучшенного или оптимизированного извлечения нефти и газа. Инженеры-нефтяники могут использовать настоящее изобретение для прогнозирования реакции коллектора на планируемую стратегию нагнетания, чтобы определить какие стратегии обеспечат оптимальное извлечение. Эксплуатация нефтяного месторождения может включать разработку стратегий "чистки", предусматривающих контроль над возрастанием дебита в нагнетательных скважинах, или оптимизацию графиков планово-профилактического ремонта, когда скважины на время закрываются. Кроме того, настоящее изобретение предоставляет критерий для долгосрочных эффектов, когда изменения в скважине влияют на другие скважины, что дает возможность лучшего управления и оптимизации потока. Структурная информация, предоставляемая настоящим изобретением, поможет при решении некоторых общих практических вопросов, таких как определение, где важны геомеханические эффекты, связанные с напряжением; а где сбросы и разломы играют главную роль в режиме подземного течения между парами скважин; определение направленных или затрудненных потоков (включая определение так называемых зон "сверхпроницаемости"), и улучшение условия применения обычных моделей коллектора для подземного состояния, используя более точные геостатические данные. Еще одно применение изобретения заключается в том, что посредством экстраполирования данных существующих нагнетательных и добывающих скважин может быть разработана стратегия загущения,предусматривающая бурение и добавление новых добывающих скважин в местах, которые оптимизируют общую добычу коллектора, и предотвратят обход карманов углеводородов в залежи. Этот способ может быть также использован в сочетании с другими независимыми данными, например, при исследовании двухточечных корреляций в области микро-сейсмичности, связанной с разрушением при сбросе в подземной области, чтобы свести к минимуму риск и установить механизм диффузии в эпицентре (гидравлический, геомеханический или и тот, и другой). В этот документ могут быть внесены улучшения и изменения без выхода за рамки настоящего изобретения. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Вычислительная система для моделирования поведения коллектора углеводородов с целью управления потоком текучей среды внутри коллектора, которая содержит модуль анализа, анализирующий данные добычи нефтяного месторождения посредством выполнения программных команд, которые включают оптимальную регрессионную модель, представляющую нагнетательные и добывающие скважины, характеристики потока текучей среды которых сильно коррелируют с характеристиками текучей среды интересующей скважины; выполняющий программные команды, использующие метод критерия ограниченной информации для определения пар скважин, которые вносят статистически значимую информацию в оптимальную регрессионную модель; выполняющий программные команды, в результате которых получают статистическую модель коллектора, элементы которой являются произведением соответствующих элементов оптимальной регрессионной модели и матрицы значимости; и средство управления и/или воздействия для корректировки потока текучей среды коллектора в одной или более представляющих интерес скважинах для управления потоком текучей среды в ответ на реакцию статистической модели коллектора, составленной модулем анализа. 2. Система по п.1, отличающаяся тем, что средство управления регулирует производительность одной или более скважин. 3. Система по п.1 или 2, отличающаяся тем, что средство управления регулирует вытеснение или схему нагнетания в нагнетательной скважине. 4. Система по любому из предшествующих пунктов, отличающаяся тем, что средство управления выполнено с возможностью выявления положения загущающих скважин, а затем и управления ими. 5. Система по любому из предшествующих пунктов, отличающаяся тем, что средство управления выполнено с возможностью автоматического управления одной или более скважинами. 6. Система по любому из предшествующих пунктов, отличающаяся тем, что средство управления выполнено с возможностью управления закачиванием воды, газа или другой текучей среды в коллектор. 7. Система по п.6, отличающаяся тем, что текучей средой является углекислый газ. 8. Система по любому из предшествующих пунктов, отличающаяся тем, что метод ограниченной информации включает байесовский метод. 9. Система по любому из предшествующих пунктов, отличающаяся тем, что матрица значимости является бинарной матрицей значимости. 10. Система по любому из предшествующих пунктов, отличающаяся тем, что для создания оптимальной регрессионной модели для нагнетательных и добывающих скважин используется множественная линейная регрессионная модель. 11. Система по п.10, отличающаяся тем, что множественная линейная регрессионная модель:(e) определяет модель прогнозируемой среднеквадратичной ошибки для заданного временного интервала;(f) минимизирует прогнозируемую среднеквадратичную ошибку для получения формальной множественной линейной регрессионной модели;(g) осуществляет поиск оптимальной регрессионной модели на основании предлагаемой стратегии выбора наилучшей модели, причем данная стратегия заключается в автоматическом прямом переборе вариантов модельного пространства прицельно по всем возможным парам скважин, используя модифицированный байесовский информационный критерий (BIC); и(h) получает оптимальную регрессионную модель, когда (a) R2 превышает заданное значение, в то время как BIC еще возрастает, (b) R2 уменьшается или (с) достигается заданное количество итераций. 12. Система по любому из предшествующих пунктов, отличающаяся тем, что временной интервал составляет один месяц. 13. Система по пп.1, 10 и 11, отличающаяся тем, что оптимальная регрессионная модель определяется из массива множественных линейных регрессионных моделей, причем разработана стратегия выбора наилучшей модели в режиме прицельного автоматического перебора вариантов модельного пространства с целью сравнения различных моделей с использованием модифицированного байесовского информационного критерия (BIC). 14. Система по пп.1, 10 и 11, отличающаяся тем, что для небольших коллекторов с малым количеством нагнетательных скважин используется информационный критерий Акайке (AIC). 15. Система по п.13, отличающаяся тем, что модель с наибольшим значением BIC выбирается при одновременно возрастающем коэффициенте детерминации (R2). 16. Система по любому из предшествующих пунктов, отличающаяся тем, что полный байесовский анализ применяется к байесовской динамической линейной модели (DLM), основанной на методе Монте-Карло с использованием цепей Маркова (MCMC), причем DLM имеет те же прогнозирующие параметры, что и прогнозирующие параметры, определенные в оптимальной регрессионной модели. 17. Система по п.16, отличающаяся тем, что полный байесовский анализ дополнительно включает:(h) определение байесовской DLM, в которой DLM модель имеет те же прогнозирующие параметры, что и прогнозирующие параметры, определенные в оптимальной регрессии, с соответствующими случайными ошибками, взаимно независимыми и распределенными по нормальному закону с нулевым математическим ожиданием, и конечными дисперсиями;(i) использование допущения априорного распределения для неизвестных параметров для DLM модели, где соответствующие дисперсии имеют распределения хи-квадрат;(j) использование функции правдоподобия неизвестных параметров;(k) вычисление плотностей совместных апостериорных распределений неизвестных параметров;(l) вычисление соответствующих плотностей полного условного распределения каждого параметра в моделях;(m) применение алгоритма выборочного метода Гиббса для непосредственного получения плотностей полного апостериорного распределения неизвестных параметров; и(n) получение матрицы значимости, исходя из плотности апостериорного распределения коэффициента регрессии, причем если плотность апостериорного распределения коэффициента регрессии имеет центр в нуле, то этот коэффициент наиболее вероятно равен нулю, в противном случае этот коэффициент равен единице. 18. Система по п.16, отличающаяся тем, что предлагаемая байесовская DLM относится к модели квадратичного роста, в которой случайные ошибки соответствуют уровню, росту и изменению роста для основного процесса давления во время t. 19. Система по п.16, отличающаяся тем, что выборочный метод Гиббса и MCMC схема для моделирования предоставляют плотности полного условного апостериорного распределения полных неизвестных параметров. 20. Система по любому из предшествующих пунктов, отличающаяся тем, что оптимальная регрессионная модель, полученная из множественной линейной регрессионной модели, является вещественной матрицей. 21. Система по любому из предшествующих пунктов, отличающаяся тем, что матрица значимости,полученная из полного байесовского анализа, является бинарной.