Способ сейсмической миграции на основе использования прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора
Формула / Реферат
1. Способ обработки сейсмических данных, включающий создание прямых глубинных экстраполяционных операторов с переменными длинами оператора, зависящими от максимального угла наклона, требования к точности и волнового числа; создание операторных таблиц с использованием прямого глубинного экстраполяционного оператора, имеющего наименьшую длину оператора, удовлетворяющую требованию к точности при максимальном угле наклона для каждого из множества волновых чисел; и выполнение глубинной миграции с использованием прямого глубинного экстраполяционного оператора в субобласти на некоторой глубине, имеющего наименьшую длину оператора из операторных таблиц для наибольшего волнового числа в указанной субобласти на указанной глубине.
2. Способ по п.1, отличающийся тем, что этап создания операторных таблиц включает в себя
выбор максимального угла наклона;
выбор типа оператора;
выбор требования к точности для указанного типа оператора;
выбор множества волновых чисел и
выполнение следующих этапов для каждого из множества волновых чисел: выбор множества длин оператора для выбранного волнового числа и выполнение следующих этапов для каждой из множества длин оператора: определение, удовлетворяет ли выбранный тип оператора с выбранной длиной оператора выбранному требованию к точности при выбранном максимальном угле наклона и выбранном волновом числе; определение, является ли длина оператора наименьшей длиной оператора, удовлетворяющей требованию к точности при выбранном максимальном угле наклона для выбранного волнового числа, и запоминание длины оператора в операторной таблице, если длина оператора является наименьшей длиной оператора, удовлетворяющей требованию к точности при максимальном угле наклона для выбранного волнового числа.
3. Способ по п.2, отличающийся тем, что этапы, которые выполняют для каждого волнового числа, включают выбор множества пар первых полудлин оператора и вторых полудлин оператора для выбранного волнового числа; и выполнение следующих этапов для каждой из множества пар первых полудлин оператора и вторых полудлин оператора:
определение, удовлетворяет ли выбранный тип оператора с выбранной парой из первой полудлины оператора и второй полудлины оператора выбранному требованию к точности при выбранном максимальном угле и выбранном волновом числе;
определение, является ли первая полудлина оператора наименьшей первой полудлиной оператора, удовлетворяющей требованию к точности для выбранного волнового числа, и является ли вторая полудлина оператора наименьшей второй полудлиной оператора, удовлетворяющей требованию к точности для выбранного волнового числа; и
запоминание пары из первой полудлины оператора и второй полудлины оператора в операторной таблице, если первая полудлина оператора является наименьшей первой полудлиной оператора, удовлетворяющей требованию к точности для выбранного волнового числа, и если вторая полудлина оператора является наименьшей второй полудлиной оператора, удовлетворяющей требованию к точности при выбранном максимальном угле наклона для выбранного волнового числа.
4. Способ по п.1, отличающийся тем, что этап создания операторных таблиц включает в себя
выбор максимального угла наклона;
выбор типа оператора;
выбор требования к точности для указанного типа оператора;
вычисление предварительных операторных таблиц для переменных длин оператора;
выбор множества волновых чисел и
выполнение следующих этапов для каждого из множества волновых чисел: выбор наименьшей длины оператора в предварительных операторных таблицах, удовлетворяющей требованию к точности для выбранного волнового числа; и запоминание наименьшей длины оператора в операторной таблице.
5. Способ по п.4, отличающийся тем, что этапы, которые выполняют для каждого волнового числа, включают в себя
выбор пары из наименьшей первой полудлины оператора и наименьшей второй полудлины оператора в предварительных операторных таблицах, удовлетворяющей требованию к точности для выбранного волнового числа; и
запоминание пары из наименьшей первой полудлины оператора и наименьшей второй полудлины оператора в операторной таблице.
6. Способ по п.1, отличающийся тем, что этап выполнения глубинной миграции включает в себя
выбор массива сейсмических данных;
выбор диапазона глубин в массиве сейсмических данных;
выбор субобласти для каждого значения глубины из выбранного диапазона глубин;
определение скоростной модели для указанного массива сейсмических данных и диапазона глубин;
определение наименьшей скорости в каждой субобласти на скоростной модели;
выбор операторной таблицы с переменными длинами оператора;
выбор множества частот в выбранной субобласти и
выполнение следующих этапов для каждой из множества частот, для каждого значения глубины из выбранного диапазона глубин и для каждой субобласти на данной глубине: вычисление наибольшего волнового числа в субобласти по частоте и наименьшей скорости в этой субобласти; выбор максимальной длины оператора из операторной таблицы для вычисления наибольшего волнового числа; применение операторов из операторной таблицы с длинами оператора, не превышающими максимальную длину оператора в выбранной субобласти.
7. Способ по п.6, отличающийся тем, что операторная таблица с переменными длинами оператора включают прямые экстраполяционные операторы с переменными длинами оператора.
8. Способ по п.6, отличающийся тем, что этап выбора операторной таблицы с переменными длинами оператора дополнительно включает интерполяцию операторной таблицы с переменными длинами оператора.
9. Способ по п.6, отличающийся тем, что длина каждого оператора включает пару из первой полудлины оператора и второй полудлины оператора.
10. Способ по п.2, отличающийся тем, что этап выбора типа оператора включает применение следующей формулы:
где Р(хi, уj, w, z+Dz) является сейсмическим волновым полем в точке с горизонтальными координатами хi=iъDх, уj=jъDу и глубиной z+Dz; w является угловой частотой; Р(хi, уj, w, z) является сейсмическим волновым полем в субобласти D на глубине z; Dх, Dу и Dz являются длинами шагов в направлении х-, у- и z-координат соответственно; L(kwmax(D, z)) и M(kwmax(D, z)) являются полудлинами оператора в направлении х- и у-координат соответственно, для наибольшего волнового числа kwmax(D, z) в субобласти D на глубине z; W(xi, уj, kw(xi, yj, z), Dz) является прямым глубинным экстраполяционным оператором; и kw(хi, уj, z) является локальным волновым числом.
11. Способ по п.10, отличающийся тем, что волновое число kw(хi, yj, z) задают формулой
где с(хi, yj, z) является локальной скоростью распространения.
12. Способ по п.10, отличающийся тем, что наибольшее волновое число kwmax(D, z) для частоты w в субобласти D на глубине z задают формулой
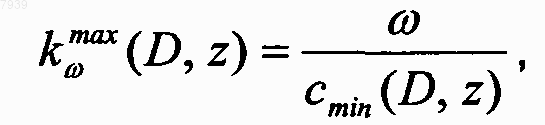
где cmin(D, z) является наименьшей скоростью в субобласти D на глубине z.
13. Способ по п.2, отличающийся тем, что этап выбора типа оператора включает применение следующей формулы:
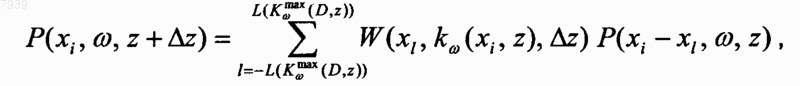
где Р(хi, w, z+Dz) является сейсмическим волновым полем в точке с горизонтальной координатой хi=iъDх и глубиной z+Dz; w является угловой частотой; P(xi, w, z) является сейсмическим волновым полем в субобласти D на глубине z; Dх и Dz являются длинами шагов в направлении х- и z-координат соответственно; L(kwmax(D, z)) является полудлиной оператора для наибольшего волнового числа kwmax(D, z) в суб-области D на глубине z в направлении х-координаты; W(xi, kw(хi, z), Dz) является прямым глубинным экстраполяционным оператором; и kw(хi, z) является локальным волновым числом.
14. Способ по п.13, отличающийся тем, что волновое число kw(хi, z) задают формулой

где c(xi, z) является локальной скоростью распространения.
15. Способ по п.2, отличающийся тем, что этап выбора типа оператора включает применение следующей формулы:
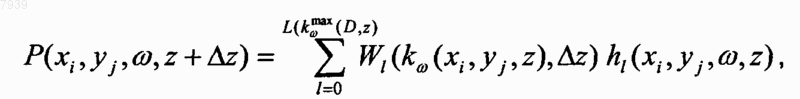
где P(xi, yj, w, z+Dz) является сейсмическим волновым полем в точке с горизонтальными координатами хi=iъDх, уj =jъDу и глубиной z+Dz; w является угловой частотой; Р(хi, уj, w, z) является сейсмическим волновым полем в субобласти D на глубине z; Dх, Dу и Dz являются длинами шагов в направлении х-, у- и z-координат соответственно; L(kwmax(D, z)) является длиной оператора для наибольшего волнового числа kwmax(D, z) в субобласти D на глубине z; Wl(kw(xi, yj, z), Dz) является прямым глубинным экстраполяционным оператором, выраженным в цилиндрических координатах; kw(хi, уj, z) является локальным волновым числом; и hl(xi, yj, w, z) являются вспомогательными полями, полученными в результате применения рекурсивных 2D-фильтров Чебышева к сейсмическому волновому полю P(xi, уj, w, z).
Текст
007939 Область техники, к которой относится изобретение Изобретение относится, главным образом, к области геофизической разведки. В частности, оно связано с обработкой сейсмических данных. Более конкретно, изобретение относится к способу сейсмической миграции на основе использования прямых экстраполяционных операторов с динамически переменной длиной оператора. Предшествующий уровень техники Использование трхмерной (3D) сейсморазведки привело к увеличению эффективности бурения в нефтяной и газовой индустрии. Однако 3D-сейсмические методы пока ещ являются дорогостоящими в вычислительном отношении. Ключевым моментом при обработке 3D-сейсмических данных является операция миграции из-за е 3D-характера и возникающих при этом вычислительных затрат. Точность,устойчивость и эффективность 3D-миграции определяется применяющейся технологией экстраполяции волнового поля. Таким образом, желательно, чтобы сами алгоритмы, применяющиеся в 3D-миграции,были точными, устойчивыми и эффективными, особенно, когда рассматривается 3D-миграция до суммирования сейсмограмм. Большое число алгоритмов, используемых в двумерной (2D) миграции, оказались неэффективными при обработке 3D-данных. Например, непрямые конечно-разностные методы экстраполяции имеют преимущество, так как являются безусловно стабильными, но их недостаток заключается в трудности распространения на обработку 3D-данных. Наиболее общий непрямой 3D-метод основан на операторе разложения на компоненты по переменным направлениям. Ошибки при разложении, присущие этим методам, при обработке 3D-данных переносятся в несферически симметричные импульсные характеристики,которые становятся непригодными для углов наклона более 45. В методах разложения возникают ошибки, которые в значительной мере зависят от наклона и азимута отражающей границы, что приводит к появлению ошибок в положении отражающей границы. Аналогично, двухпроходные методы имеют проблемы при учте изменений скорости по горизонтали. Напротив, прямые методы экстраполяции, которые аппроксимируются оператором экстраполяции,таким как пространственный фильтр конечной длительности, легко распространяются на 3D-случай. Трудности с применением методов прямой экстраполяции заключаются в том, что условия устойчивости не выполняются автоматически. Условия устойчивости заключаются в том, что на любой частоте амплитуда не будет возрастать экспоненциально с глубиной. Устойчивость должна обеспечиваться тщательной конструкцией операторов экстраполяции. Операция продолжения трхмерного сейсмического волнового поля в нижнее полупространство может быть выполнена последовательно, по одной частоте за один раз, при помощи двумерной свртки со сферически симметричным оператором, зависящим от частоты и скорости. Эта экстраполяция в нижнее полупространство, выполняющаяся независимо для каждой частоты, лежит в основе 3D-конечноразностной глубинной миграции. Вычислительная эффективность 3D-глубинной миграции прямо зависит от эффективности этой глубинной экстраполяции. Для этих технологий, чтобы получить наджные и интерпретируемые результаты, продолжение волнового поля в нижнее полупространство должно обеспечивать экстраполяцию волнового поля в неоднородной среде с минимумом возникающих при вычислительном процессе искажений в диапазоне частот и углов распространения волн.Holberg, О. "К вопросу об оптимальном одностороннем распространении волны", Geophysical Prospecting, т. 36, 1988, стр. 99-114, впервые показал возможность прямой экстраполяции в нижнее полупространство с оптимизированными операторами. Holberg предложил технологию исключительно для 2Dглубинной миграции путм обобщения обычных конечно-разностных выражений в частотной области. Эта технология создат оптимизированные пространственно симметричные операторы свртки, коэффициенты которых могут быть заранее вычислены перед миграцией и представлены в табличной форме. Отношение между текущей частотой и локальной скоростью используется для определения соответствующего оператора в каждой точке сетки в процессе продолжения волнового поля в нижнее полупространство, их пространственно-частотные характеристики согласуются с желаемой характеристикой фазовых сдвигов в диапазоне частот и углов распространения волн для контроля вычислительных искажений. Holberg технология может применяться при обработке данных с горизонтальными изменениями скорости. Однако этот способ применим только для 2D миграции.(1988) на 3D-миграцию. Экстраполяция волнового поля осуществляется в пространственно-частотной области путм зависящей от координат пространственной свртки с рекурсивными экстраполяционными операторами Кирхгофа, основанными на операторах фазового сдвига. Оптимизированные операторы заранее вычисляются и запоминаются в виде таблиц для всего диапазона волновых чисел. Экстраполяция выполняется рекурсивно в пространственной области, поэтому могут обрабатываться данные как с вертикальными, так и горизонтальными изменениями скорости. Метод Блэкьера (Blacquiere) и др. является точным, но это полностью 3D-технология и поэтому дорогая в вычислительном отношении.(ноябрь, 1991), стр. 1778-1785, представил более эффективную 3D-схему, основанную на McClellan пре-1 007939 образовании, которая дат численно изотропные операторы экстраполяции. Обычно в ссылках она известна как Hale-McClellan схема. Заданные коэффициенты зависящих от частоты и скорости одномерных фильтров, которые подобны использующимся при выполнении 2D-глубинной миграции, McClellan преобразования приводят к алгоритму 3D-глубинной миграции. Поскольку коэффициенты двумерных глубинных экстраполяционных фильтров никогда явно не вычисляются и не запоминаются, то требуются только коэффициенты соответствующих одномерных фильтров. Применение двумерных экстраполяционных фильтров дат улучшение, которое только линейно пропорционально числу коэффициентов N в соответствующих одномерных фильтрах, тогда как стоимость свртки с двумерными фильтрами обычно возрастает пропорционально N2. Однако метод Hale имеет численную анизотропию. Две Soubaras публикации: Soubaras, R. "Прямая 3-D миграция, использующая эквипульсирующее полиномное разложение и синтез Лапласа", 62nd Ann., Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, 1992, стр. 905-908, and Soubaras, R."Прямая 3-D-миграция, использующая эквипульсирующее полиномное разложение и синтез Лапласа", Geophysics, т. 61,5 (сентябрь-октябрь, 1996), стр. 1386-1393,усовершенствуют Hale-McClellan схему. Soubaras (1992, 1996) метод использует разложение с применением дифференциальных операторов второго порядка вместо McClellan преобразования. Soubaras (1992,1996) метод также использует Remez алгоритм для расчта коэффициентов экстраполяционного оператора и дифференциальных операторов. В этом методе в большей степени исключается численная анизотропия, и по вычислительной стоимости он сравним с Hale-McClellan схемой.Soubaras подход использует преимущества оператора со сферической симметрией, как и вMcClellan преобразованиях, но избегает вычисления 2D-фильтра, аппроксимирующего косинус волновых чисел. В этом методе определяется оператор Лапласа, который аппроксимируется суммой двух 1Dфильтров, аппроксимирующих вторые производные, и при помощи полинома аппроксимируется точный экстраполяционный оператор. Операторы вторых производных и полиномное разложение вычисляются при помощи Remez перестановочного алгоритма.Sollid, А. и Arntsen, В. "Стоимость эффективной однопроходной глубинной 3D-миграции", Geophysical Prospecting, т. 42, 1994, стр. 755-716, делает Soubaras (1992, 1996) схему более эффективной в отношении затрат. Sollid и Arntsen (1994) использовали адаптированные по частоте оптимизированные операторы производных. Используется разложение с применением дифференциальных операторов второго порядка, но коэффициенты разложения и дифференциальные операторы рассчитываются с использованием метода наименьших квадратов, а не Remez алгоритма. Для обеспечения точности и эффективности результирующей волновой экстраполяции дифференциальные операторы второго порядка переменной длины для каждого волнового числа имеют различные спектры и длительность.Ann., Internat. Mtg., Soc. Expl. Geophys., Expanded Abstracts, стр. 1148-1151, представляет метод с ограниченным прямым оператором, являющийся модификацией полной 3D-схемы, рассмотренной выше в Blacquiere и др. (1989), который должен сделать эту схему более эффективной в вычислительном отношении. Число независимых коэффициентов оператора ограничивается для уменьшения числа требуемых компьютерных операций с плавающей запятой, в результате увеличивается компьютерная эффективность. Внутренние коэффициенты в ядре экстраполяционного оператора вычисляются стандартным способом. Остающиеся внешние коэффициенты в операторе, относящиеся к очень большим углам и распространению быстрозатухающих волн, изменяются только как функции радиуса и являются постоянными внутри радиальных интервалов. Таким образом, существует потребность в создании прямого метода глубинной экстраполяции для 2D- и 3D-сейсмической миграции, который является точным, устойчивым и эффективным. Сущность изобретения Настоящее изобретение предлагает способ сейсмической миграции, в котором используют прямые экстраполяционные глубинные операторы с динамически переменной длиной оператора. Прямые глубинные экстраполяционные операторы создают с переменными длинами оператора, зависящими от максимального угла наклона, требования к точности и волнового числа. Затем создают операторные таблицы с использованием прямых глубинных экстраполяционных операторов. В дополнительных вариантах изобретения глубинную миграцию выполняют с использованием прямых глубинных экстраполяционных операторов в табличной форме. Краткое описание чертежей Изобретение и его преимущества более легко могут быть поняты из последующего подробного описания со ссылками на сопроводительные чертежи, где фиг. 1 является блок-схемой, иллюстрирующей этапы обработки в первом варианте способа, реализуемого данным изобретением, который предназначен для создания прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора; фиг. 2 - блок-схемой, иллюстрирующей этапы обработки во втором варианте способа, реализуемого данным изобретением, предназначенного для создания прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора; фиг. 3 - блок-схемой, иллюстрирующей первоначальные этапы обработки с использованием таблиц-2 007939 прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора, которая продолжается на фиг. 4; и фиг.4 - блок-схемой, иллюстрирующей окончательные этапы обработки с использованием таблиц прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора, которая является продолжением блок-схемы по фиг. 3. Поскольку данное изобретение будет описано посредством предпочтительных вариантов реализации, то следует понимать, что оно не ограничивается ими. Напротив, изобретение предполагает охватить все альтернативы, модификации и эквиваленты, которые могут быть включены в объм изобретения в соответствии с формулой. Сведения, подтверждающие возможность осуществления изобретения Настоящее изобретение является способом сейсмической миграции, в котором используют прямые экстраполяционные глубинные операторы с динамически переменной длиной оператора. Способ, реализуемый данным изобретением, применим к методам, приведенным в вышеописанных публикациях, а также любым другим методам, производным или похожим на методы, описанные в этих публикациях. Продолжение волнового поля в нижнее полупространство преобразует сейсмическое волновое поле Р(х, у, , z) в точке с горизонтальными координатами х, у и глубиной z в сейсмическое волновое поле Р(х, у, , z+z) на глубине z+z посредством свртки с экстраполяционным оператором W(x, у, k(х, у,z), z). Сейсмическое волновое поле Р(х, у, , z) находится в пространственно-частотной области, которая трансформируется в случае необходимости из пространственно-временной области при помощи прямого преобразования Фурье. Здесь х и у являются горизонтальными пространственными координатами, обычно это продольное и поперечное направления, на соответствующей площади сейсмической съмки, в которой были получены данные. Интервал z является интервалом пространственной выборки или длиной шага z-координаты в вертикальном направлении, где глубина z устанавливается положительной и отмеряется в нижнем направлении. Локальное волновое число k(х, у, z) определяется формулой где =2f является угловой частотой для частоты f, а c(х, у, z) является локальной скоростью распространения в среде в пространстве (х, у, z). Таким образом, прямая глубинная экстраполяция может быть выражена в пространственно-частотной области при помощи следующей двумерной пространственной свртки вдоль горизонтальных х- и у-координат Экстраполяция, приведенная в уравнении (2), производится рекурсивно в нижнее полупространство для всех представляющих интерес уровней глубины z. Один из способов изменения скорости в вертикальном направлении заключается в задании различных значений скорости для каждого уровня глубиныz. Кроме того, скорость может изменяться по горизонтали в направлении х- и у-координат для каждого уровня глубины z. Оператор экстраполяции W(x, у, k(х, у, z), z) в уравнении (2) является аппроксимацией обратного пространственного преобразования Фурье точного экстраполяционного оператора D(kx, ky, k, z) для прямой глубинной экстраполяции. Точный экстраполяционный оператор D(kx, ky, k, z) задатся в пространстве частота-волновое число оператором фазового сдвига где kx и kу являются горизонтальными волновыми числами по х- и у-координатам соответственно. Строго говоря, оператор фазового сдвига правомерен только для однородной среды, которой является среда с отсутствием вариаций скорости. В результате обратного пространственного преобразования Фурье оператора фазового сдвига в уравнении (2) создатся Релеевский оператор в пространственночастотной области, однако, чтобы оказаться полезным, он должен быть ограничен по полосе и укорочен. В применяемом на практике альтернативном варианте прямой экстраполяционный оператор обычно аппроксимируется в пространственно-частотной области. Таким образом, целью прямой глубинной экстраполяции является создание прямого оператора экстраполяции W(x, у, k(х, у, z), z), который одновременно является точным, устойчивым и эффективным. Создание прямого оператора экстраполяции W(x, у, k(х, у, z), z), который является точным, означает, что преобразование Фурье W(kx, ky, k, z) достаточно близко аппроксимирует точный экстраполяционный оператор D(kx, ky, k, z), приведенный в уравнении (3). Таким образом, разность между операторами D(kx, ky, k, z) и W(kx, ky, k, z) должна быть минимальной для данной частотыи скорости с(х, у, z), соответствующих данному k(х, у, z). Разность между операторами D(kx, kу, k, z) и W(kx, ky,-3 007939k, z) измеряется по определнному стандарту в пространстве частота-волновое число в соответствующем диапазоне волновых чисел, определяемых условиями распространения или полосой пропускания оператора. Область полосы пропускания обычно включает все волновые числа, которые меньше, чем граничные волновые числа kс(x,max) и kc(y,max), определяемые уравнениями где x,max и y,max являются максимальными углами наклона, для которых выполняется точная миграция в направлении х-координат и у-координат соответственно. Заметим, если x,max=y,max, то kc(x,max)=kc(y,max). Таким образом, экстраполяционный оператор удовлетворяет следующим требованиям к точности в полосе пропускания волновых чисел гдепредставляет соответствующий стандарт в пространстве частота-волновое число. Граничные волновые числа kc(x,max) и kc(y,max) определяют максимальный угол наклона, удовлетворяющий требованиям к точности прямого экстраполяционного оператора. Создание прямого экстраполяционного оператора W(x, у, k(х, у, z), z), который является устойчивым, означает, что абсолютное значение амплитуды характеристики волновых чисел W(kx, ky, k, z) приближается как можно ближе к единице в полосе пропускания волновых чисел и ограничивается или гасится для углов распространения, превышающих заданный максимальный угол наклона, и в области быстрозатухающих волн. Этот последний диапазон волновых чисел называется областью непропускания оператора. Область непропускания обычно определяется всеми волновыми числами, превышающими или равными граничному волновому числу, а также меньшими или равными волновым числам Найквиста kx,Nyq, ky,Nyq, определяемых уравнением где х и у являются интервалом пространственной выборки или длиной шага в горизонтальном направлении по х- и у-координатам соответственно. Заметим, что если х=у, то kx,Nyq=kyNyq. Таким образом, прямой экстраполяционный оператор удовлетворяет следующему условию устойчивости в полосе пропускания волновых чисел: и следующему условию устойчивости в полосе непропускания волновых чисел: Стабильность характеристики очень важна, поскольку прямой экстраполяционный оператор будет применяться рекурсивно. Создание прямого экстраполяционного оператора W(x, у, k(х, у, z), z), который является эффективным, означает, что применение оператора W в миграционной схеме является недорогим в вычислительном отношении. Для вычислительной эффективности необходима дискретная версия уравнения (2). Пусть i, j, l и m будут целыми числами и пусть х, у и z будут длиной шага в направлении по х-, у- иz-координатам соответственно, как было определено выше. Тогда положение на горизонтальной плоскости может быть задано дискретно значениями хi=iх и уj=jy. Дискретная экстраполяция в нижнее полупространство трансформирует дискретное представление волнового поля Р(хi, yj, , z) в точке с координатами хi, уj на горизонтальной плоскости и уровне глубины z в волновое поле Р(хi, yj, , z+z) на глубине z+z путм свртки с дискретным экстраполяционным оператором W(xi, yj, k(хi, yj, z), z). Дискретное волновое число k(xi, yj, z) определяется тогда следующей дискретной версией, заменяющей уравнение (1): Аналогично, для второго равенства в уравнении (2) дискретная версия прямой глубинной экстраполяции может быть выражена в трх измерениях формулой где L и М получили название полудлин оператора W в х- и у-направлениях соответственно. Целые числаL и М называются полудлинами оператора, поскольку число коэффициентов в экстраполяционном операторе W равно (2L+1)(2 М+1). Для справки, 3D-версия уравнения (10) может быть уменьшена непосредственным образом до 2Dверсии, которая определяется уравнением Заметим, что полудлины L и М в уравнениях (10) и (11) определяют длину или размер точного экстраполяционного оператора W, и таким образом, эффективность экстраполяционного метода. В принципе полудлины оператора следовало бы сделать бесконечными для достижения наибольшей точности. На практике, для компьютерной реализации эти полудлины должны быть конечными. В частности, полудлины оператора должны быть минимизированы для повышения эффективности компьютерной обработки. Как будет описано ниже со ссылкой на настоящее изобретение, полудлины оператора могут быть сделаны оптимально зависящими от максимального волнового числа k(хi, yj, z) на заданной глубине z или в субобласти D на этом уровне глубины z.Holberg (1988) определяет коэффициенты трансформированного экстраполяционного оператора W для 2D-случая в соответствии с уравнением (11). Однако этот метод применим только для 2D. Blacquiere и др. (1989) распространяет этот метод на 3D-случай в соответствии с уравнением (10). Однако этот способ вс ещ дорогой в вычислительном отношении. Hale (1991) вводит более эффективную схему, основанную на McClellan преобразовании для вычисления коэффициентов экстраполяционного оператора W. Однако этот метод имеет численную анизотропию. Soubaras (1992, 1996) предлагает улучшенный способ,использующий дифференциальные операторы второго порядка вместо McClellan преобразования. Однако этот метод вс ещ имеет численную анизотропию. Sollid, А. и Arntsen, В. (1994) использовали адаптированные по частоте оптимизированные операторы производных для улучшения вычислительной эффективности Soubaras метода. Способы для применения экстраполяционного оператора в соответствии с Hale-McClellan методом,как обсуждалось выше для Hale (1991), Soubaras (1992, 1996) и Sollid, А. и Arntsen, В. (1994) являются двухступенчатыми алгоритмами. Первоначально рекурсивные 2D-фильтры Чебышева применяются к волновому полю Р(xi, уj, , z) на глубине z, в результате создаются вспомогательные поля hl(xi, yj, , z). Затем волновое поле на экстраполируемой в нижнее полупространство глубине z+z вычисляется по формуле где Wl(k(xi, yj, z), z) является экстраполяционным оператором, выраженным теперь в цилиндрических координатах. Для всех упомянутых выше типов схем экстраполяционные коэффициенты должны быть рассчитаны для последовательности значений k волновых чисел в диапазоне от 0 до волнового числа Найквиста, которое определяется максимальным волновым числом Найквиста из уравнения (6) или равно , если координаты нормализованы. В настоящем изобретении для этих типов экстраполяционных схем показано, что полудлина оператора L может быть сделана оптимально зависящей от максимального волнового числа k на заданной глубине z или в субобласти D на этом уровне глубины z. Такая оптимизация дат увеличение вычислительной эффективности. Эта вычислительная эффективность затем может быть повышена при использовании рассмотренной выше методики с ограничивающим оператором,предложенной Mittet, R. (2002). Стандартная методика заключается в придании полудлине оператора постоянного значения для всех волновых чисел k. Общеизвестно, что с увеличением максимального заданного угла полудлина оператора также должна быть увеличена, если численная точность должна оставаться фиксированной. Поэтому для максимального угла наклона в 55 может потребоваться полудлина оператора, равная 8, а для максимального угла наклона в 70 может потребоваться полудлина оператора, равная 16. Для полного 3D-onepaтopa увеличение полудлины в 2 раза в этом случае увеличивает вычислительные работы более чем в 4 раза. Полудлина экстраполяционного оператора, равная 3, 5 и 12, часто ассоциируется с точностью для углов наклона в 30, 50 и 70 соответственно. Имеется, однако, другой факт, который не является очевидным и не используется. Для заданного максимального угла наклона при фиксированной численной точности требуемая полудлина оператора изменяется с волновым числом k. Зависимость заключается в том, что полудлина должна быть увеличена с увеличением k. Таким образом, объм вычислительной работы при глубинной экстраполяции может быть значительно уменьшен путм создания операторных таблиц с переменными полудлинами опе-5 007939 ратора. Имеется несколько способов создания таких операторных таблиц. Первый способ заключается непосредственно в программах оптимизации оператора. Методика состоит в том, что для каждого волнового числа k вычисления начинаются с самых маленьких значений полудлин L(k) и М(k) для 3D-случая,или только полудлины L(k) для 2D-случая. Затем величина каждой полудлины увеличивается с шагом,равным 1, пока не будет достигнута надлежащая сходимость. Эта методика иллюстрируется на фиг. 1,где приведена блок-схема, показывающая этапы обработки для создания таблиц прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора в первом варианте реализации способа. На этапе 101 выбирается максимальный угол наклона, для которого миграция должна выполняться с необходимой точностью. В альтернативном варианте максимальный угол наклона, для которого миграция должна выполняться с необходимой точностью, выбирается в направлении х-координат и укоординат. Обычно направления по х-координатам и у-координатам соответствуют продольному и поперечному направлениям на площади сейсмической съмки, в которой были получены сейсмические данные. В другом альтернативном варианте максимальные углы наклона выбираются во всех направлениях. На этапе 102 выбирается тип прямого экстраполяционного оператора для глубинной миграции. В качестве примера, который не является ограничивающим, можно отметить, что способ, реализуемый данным изобретением, применим к методам, приведенным в вышеописанных публикациях, а также любым другим методам, производным или похожим на методы, описанные в этих публикациях. Таким образом, например, 3D-прямая глубинная экстраполяция может быть осуществлена с применением уравнения (10) и 2D-прямая глубинная экстраполяция может быть реализована с применением уравнения (11). На этапе 103 выбираются требования к точности для максимальных углов наклона, выбранных на этапе 101, и типа прямого глубинного экстраполяционного оператора, выбранного на этапе 102. Требования к точности выбираются для получения ответа на вопрос: является ли полудлина оператора, определяющая объм прямых глубинных экстраполяционных операторов, достаточно большой. Например,требования к точности могут включать условие, что выбранный прямой экстраполяционный оператор удовлетворяет требованиям к точности в полосе пропускания волновых чисел, определяемой вышеприведенным уравнением (5). Включение этого требования к точности может потребовать вычисления граничных волновых чисел kс(x,max) и kс(y,max), задаваемых уравнением (4), для определения диапазона полосы пропускания. Граничные волновые числа зависят от максимальных углов наклона x,max и y,max, в направлении х-координат и у-координат соответственно, которые были выбраны на этапе 101. На этапе 104 выбирается волновое число k. Выбор волнового числа k предпочтительно делать систематизированным образом для повышения вычислительной эффективности, хотя систематизированный выбор волнового числа k не является требованием изобретения. Например, диапазон волновых чисел k может начинаться от наименьшего волнового числа, равного 0, до наибольшего волнового числа,равного волновому числу Найквиста. Затем выбор волнового числа k может начинаться с наименьшего представляющего интерес волнового числа и продолжаться последовательно до наибольшего представляющего интерес волнового числа, или наоборот продолжаться последовательно от представляющего интерес наибольшего волнового числа к наименьшему. На этапе 105 выбирается длина оператора для волнового числа k, выбранного на этапе 104. Длину оператора предпочтительно выбирать систематизированным образом для повышения вычислительной эффективности, хотя систематизированный выбор длин оператора не является требованием изобретения. Например, выбор длин оператора может начинаться с низких значений полудлин оператора и продолжаться последовательно с приращением на 1. Для 2D-случая, в соответствии с уравнением (11), длина оператора определяется полудлиной L Таким образом, полудлину L(k) в х-направлении следует подбирать для волнового числа k, выбранного на этапе 105. Для 3D-случая, как показано в уравнении (10), общая длина оператора определяется полудлинами L и М. Таким образом, полудлину L(k) в х-направлении и полудлину М(k) в у-направлении следует подбирать для волнового числа k, выбранного на этапе 105. На этапе 106 определяют, удовлетворяет ли тип оператора, выбранного на этапе 102, с длиной оператора, выбранной на этапе 105, требованиям к точности, выбранным на этапе 103 для максимальных углов наклона, выбранных на этапе 101. Для 2D-случая длину оператора следует задавать полудлинойL(k) и для 3D-случая длину оператора следует задавать парой полудлин L(k) и М(k). Если ответ отрицательный, то требования к точности не удовлетворяются, тогда процесс возвращается на этап 106 для выбора другой длины оператора. Если ответ положительный, то требования к точности удовлетворяются, и тогда процесс продолжается на этапе 108. На этапе 107 определяют, является ли длина оператора, выбранная на этапе 105, наименьшей длиной оператора, удовлетворяющей требованиям к точности для волнового числа k, выбранного на этапе 104. Для 2D-случая длину оператора следует задавать полудлиной L(k) и для 3D-случая длину оператора следует задавать парой полудлин L(k) и М(k). Если ответ отрицательный, то длина оператора не-6 007939 является наименьшей, удовлетворяющей требованиям к точности, тогда процесс возвращается на этап 105 для выбора другой длины оператора. Если ответ положительный, то длина оператора является наименьшей, удовлетворяющей требованиям к точности, и тогда процесс продолжается на этапе 108. На этапе 108 длина оператора, определнная на этапе 105, размещается в операторной таблице. Для 2D-случая длину оператора следует задавать полудлиной L(k) и для 3D-случая длину оператора следует задавать парой полудлин L(k) и М(k). На этапе 109 определяют, удовлетворяет ли всем требованиям представляющее интерес волновое число k, чтобы быть выбранным на этапе 104. Если ответ положительный, то представляющее интерес волновое число k сохраняется, и тогда процесс возвращается на этап 104 для выбора другого волнового числа k. Если ответ отрицательный, и не остатся представляющих интерес волновых чисел k, тогда процесс продолжается на этапе 110. На этапе 110 процесс заканчивают. Таблица прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора создана. Вторая методика получения операторных таблиц начинается с создания комплекта операторных таблиц с полудлинами, изменяющимися от минимального до максимального значений полудлин L(k) или M(k), которые имеют минимально возможную ошибку для каждого значения волнового числа k. Затем для каждого значения k производится просмотр характеристики волновых чисел этого комплекта операторных таблиц с фиксированным критерием погрешности, в результате которого определяется оператор, имеющий самую короткую полудлину и приемлемую ошибку. Этим путм синтезируется единая,новая операторная таблица с переменными полудлинами оператора L(k) и М(k) из комплекта таблиц операторов с фиксированной длиной. Эта методика иллюстрируется на фиг. 2, на котором приведена блок-схема, показывающая этапы обработки для создания прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора во втором варианте реализации способа. На этапе 201 выбирается максимальный угол наклона, для которого миграция должна выполняться с необходимой точностью. В альтернативном варианте максимальный угол наклона, для которого миграция должна выполняться с необходимой точностью, выбирается в направлении х-координат и укоординат. Обычно направления по х-координатам и у-координатам соответствуют продольному и поперечному направлениям на площади сейсмической съмки, в которой были получены сейсмические данные. В другом альтернативном варианте максимальные углы наклона выбираются во всех направлениях. На этапе 202 выбирается тип прямого экстраполяционного оператора для глубинной миграции. В качестве примера, который не является ограничивающим, можно отметить, что способ, реализуемый данным изобретением, применим к методам, приведенным в вышеописанных публикациях, а также любым другим методам, производным или похожим на методы, описанные в этих публикациях. На этапе 203 выбирают требования к точности для максимальных углов наклона, выбранных на этапе 201, и типа прямого глубинного экстраполяционнго оператора, выбранного на этапе 202. Требования к точности выбираются для получения ответа на вопрос: является ли полудлина оператора, определяющая объм прямых глубинных экстраполяционных операторов, достаточно большой. Требованиям к точности следует выбирать таким же образом, как уже было описано выше со ссылкой на этап 103 блоксхемы на фиг. 1. На этапе 204 создают предварительные операторные таблицы для типа оператора, выбранного на этапе 202 с переменными длинами операторов, изменяющимися от возможных минимальных до максимальных значений. Предварительные операторные таблицы рассчитываются таким образом, чтобы погрешность была минимально возможной для каждого значения волнового числа k. Таким образом, требования к точности, выбранные на этапе 203, обеспечивают минимальную ошибку для каждого значения волнового числа k. Для 2D-случая, как следует из уравнения (11), длина оператора определяется полудлиной L. Таким образом, предварительные операторные таблицы следует создавать для полудлин Lmin(k), , Lmax(k) в направлении х-координаты с наименьшей возможной ошибкой для каждого значения k. Для 3D-случая,как следует из уравнения (10), длина оператора определяется полудлинами L и М. Таким образом, предварительные операторные таблицы следует создавать для полудлин Lmin(k), , Lmax(k) в х-направлении и полудлин Mmin(k), , Mmax(k) в у-направлении с минимально возможной ошибкой для каждого значения k. На этапе 205 выбирают волновое число k. Выбор волнового числа k предпочтительно делать систематизированным образом для повышения вычислительной эффективности, хотя систематизированный выбор волнового числа k не является требованием изобретения. Например, диапазон волновых чисел k может начинаться от наименьшего волнового числа, равного 0, до наибольшего волнового числа, равного волновому числу Найквиста. Затем выбор волнового числа k может начинаться с наименьшего представляющего интерес волнового числа и продолжаться последовательно до наибольшего представляющего интерес волнового числа, или, наоборот, продолжаться последовательно от представляющего интерес наибольшего волнового числа к наименьшему.-7 007939 На этапе 206 определяют наименьшую длину оператора, удовлетворяющую требованиям к точности, выбранным на этапе 203 для волнового числа k, выбранного на этапе 205. Наименьшая длина оператора определяется путм просмотра предварительных операторных таблиц, созданных на этапе 204. Наименьшую длину оператора предпочтительно выбирать систематизированным образом для повышения вычислительной эффективности, хотя систематизированный выбор длин оператора не является требованием изобретения. Например, определение наименьшей длины оператора может начинаться с минимальной длины оператора и продолжаться с последовательным увеличением до максимальной длины оператора в предварительных операторных таблицах для выбранных волновых чисел k. Для 2D-случая наименьшую длину оператора следует определять путм последовательного вычисления с возрастанием на основе использования полудлин Lmin(k), , Lmax(k). Для 3D-случая наименьшую длину оператора следует определять путм последовательного вычисления с возрастанием на основе использования пары полудлин Lmin(k), , Lmax(k) и Mmin(k), , Мmax(k). На этапе 207 наименьшую длину оператора, определнную на этапе 105, размещают в операторной таблице. Для 2D-случая длину оператора следует задавать полудлиной L(k) и для 3D-случая длину оператора следует задавать парой полудлин L(k) и М(k). На этапе 208 определяют, удовлетворяет ли всем требованиям представляющее интерес волновое число k, чтобы быть выбранным на этапе 205. Если ответ положительный, то представляющее интерес волновое число k сохраняется, и тогда процесс возвращается на этап 205 для выбора другого волнового числа k. Если ответ отрицательный, и не остатся представляющих интерес волновых чисел k, тогда процесс продолжается на этапе 209. На этапе 209 процесс заканчивают. Таблица прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора создана. В обоих вариантах реализации изобретения, как обсуждалось со ссылкой на фиг. 1 и 2, создают операторные таблицы с переменными полудлинами оператора L(k) и M(k), зависящими от волнового числа k. Для фиксированного максимального угла распространения max и фиксированных требований к точности справедливо следующее: полудлина оператора будет увеличиваться с ростом k. В таблице приведен пример, показывающий как изменяются длины оператора L и М для ограниченного экстраполяционного оператора с максимальным углом распространения в 65 для различных интервалов волнового числа k. Реальные интервалы волновых чисел в таблице обычно будут изменяться в зависимости от таких факторов, как тип оператора, максимальный угол наклона и требования к точности. Однако общая тенденция заключается в том, что оператор с короткой полудлиной может быть использован для значений волновых чисел, составляющих от 70 до 80% от волнового числа Найквиста. Операторные таблицы с переменной длиной оператора требуют просмотра скоростной модели перед началом экстраполяции волны. Это не требует больших вычислительных затрат и может выполняться только один раз независимо от количества экстраполируемых частот. Наиболее простая процедура заключается в определении наименьшей скорости распространения на каждом уровне глубины. Прямая глубинная экстраполяция выполняется для одного значенияза один раз. Для данного уровня глубины z , когда угловая частотаи наименьшая скорость распространения cmin(z) известны, наибольшее волновое число kmax(z) для этого уровня глубины z определяется формулой Таким образом, могут быть определены необходимые максимальные полудлины экстраполяционного оператора L(k) и М(k) для этого шага глубин z. Здесь источник повышения вычислительной эффективности очевиден. Во-первых, для маленьких и промежуточных значений частотыможет сохраняться высокая численная точность с экстраполяционным оператором, имеющим короткие полудлиныL(k) и М(k). Во-вторых, в высокоскоростных зонах, таких как, например, соль, наивысшее волновое число kmax(z) будет маленьким вследствие высокого значения минимальной скорости распространенияcmin(z). Кроме того, высокая точность и большой угол наклона могут быть реализованы с относительно короткими полудлинами экстраполяционного оператора. Усовершенствование способа, реализуемого настоящим изобретением, заключается в разделении плоскости на каждой глубине z на несколько субобластей D. Вместо определения наименьшей скорости распространения Cmin(z) для всей плоскости на глубине z, определяют наименьшую скорость распространения cmin(D, z) для каждой субобласти D внутри плоскости на глубине z. Тогда, в соответствии с уравнением (13), наибольшее волновое число kmax(D, z) для этой субобласти D на уровне глубины z определяется для угловой частотыформулой Это дат дополнительное повышение эффективности, поскольку в тех субобластях, которые повсюду имеют высокую скорость распространения, могут использоваться относительно более короткие операторы. Теперь, если точка (xi, yj, z) находится в области D на глубине z, тогда 3D-прямая глубинная экстраполяция может быть усовершенствована на основе совместного использования уравнения (14) и уравнения (10), которое приводит к следующей формуле: Аналогично, 2D-прямая глубинная экстраполяция может быть усовершенствована на основе совместного использования уравнения (14) и уравнения (11), которое приводит к следующей формуле: Кроме того, прямая глубинная экстраполяция может быть усовершенствована для Hale-McClellan методики, рассмотренной выше для Hale (1991), Soubaras (1992, 1996), Sollid, А. и Arntsen, В. (1994), на основе совместного использования уравнения (14) и уравнения (12), которое приводит к следующей формуле: На фиг. 3 и 4 показаны две блок-схемы, иллюстрирующие этапы обработки для сейсмической миграции, использующей таблицы прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора. Операторные таблицы создают в результате применения способа, реализуемого настоящим изобретением, предпочтительно одним из описанных выше вариантов со ссылкой на блок-схемы на фиг. 1 и 2. На фиг. 3 приведена блок-схема, иллюстрирующая первоначальные этапы обработки, продолжение которой иллюстрируется на фиг. 4. На этапе 301 выбирают массив сейсмических данных, пригодных для глубинной миграции. Массив сейсмических данных предварительно представляется в пространственно-частотной области, трансформированной из пространственно-временной области, в случае необходимости, при помощи прямого преобразования Фурье. На этапе 302 выбирается диапазон глубин z для массива сейсмических данных, выбранных на этапе 301. Каждая глубина z представляет интервал глубины в массиве сейсмических данных. Множество глубин выбирается систематическим образом, начиная от верхнего уровня глубины в массиве сейсмических данных, последовательно следуя вниз интервал за интервалом. На этапе 303 выбирают множество субобластей D для каждой глубины z в диапазоне глубин z, выбранных на этапе 302 для массива сейсмических данных, выбранных на этапе 301. Рассмотрение субобластей D на каждой глубине z придат гибкость данному изобретению. Однако, в альтернативном варианте реализации способа согласно изобретению субобласти D на каждой глубине z не рассматриваются. Для полноты и ясности процесс обработки будет проиллюстрирован вариантом, содержащим субобласти, но возможность распространения его на вариант, не содержащий субобластей, вполне очевидна. На этапе 304 строят скоростную модель для массива сейсмических данных, выбранных на этапе 301. По скоростной модели определяют локальные скорости с(х, у, z) для диапазона глубин z, выбранных на этапе 302, и субобластей D, выбранных на этапе 303. Скоростная модель может быть построена любым из способов, известных в этой области техники. На этапе 305 определяют наименьшую скорость cmin(D, z) для каждой субобласти D, выбранной на этапе 303 для каждой глубины z. Определение наименьшей скорости в каждой субобласти следует делать-9 007939 на основе изучения скоростной модели, определнной на этапе 303. В альтернативном варианте реализации способа субобласти D для каждой глубины z не рассматриваются. Наименьшая скорость cmin(z) определяется только для каждой глубины z в диапазоне глубин z, выбранном на этапе 302, на основе изучения скоростной модели, определнной на этапе 303. Для полноты и ясности процесс обработки будет проиллюстрирован вариантом, содержащим субобласти, но возможность распространения его на вариант, не содержащий субобласти, вполне очевидна. На этапе 306 выбирают таблицу прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора для массива сейсмических данных, выбранных на этапе 301. Таблицу следует создавать способом согласно изобретению, в частности, одним из описанных вариантов со ссылками на блок-схемы по фиг. 1 и 2. Для 2D-случая длину оператора следует задавать полудлиной L(k) и для 3D-случая длину оператора следует задавать парой полудлин L(k) и М(k). Таблица прямых экстраполяционных операторов может быть создана любым из методов, известных в этой области техники. В частности, способ, реализуемый данным изобретением, применим к методам,приведенных в вышеописанных публикациях, и любым другим методам производным или подобным методам, представленных в этих публикациях. На этапе 307 таблица прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора для массива сейсмических данных, выбранных на этапе 306, в случае необходимости, может быть интерполирована для массива сейсмических данных, выбранных на этапе 301. Интерполяция позволяет создать, хранить и многократно использовать операторные таблицы приемлемого объма. Кроме того, интерполяция может быть проведена для конкретной скоростной модели, используемой для данного массива сейсмических данных, и установленных требований к точности. На этапе 308 процесс возвращают с этапа 410 на фиг. 4, в случае необходимости выбора другой частоты . На этапе 309 выбирают частотудля массива сейсмических данных, выбранных на этапе 301. Выбор частотыпредпочтительно делать систематизированным образом для повышения вычислительной эффективности, хотя систематизированный выбор частотыне является требованием изобретения. Например, выбор частотыможет начинаться с наименьшей представляющей интерес частоты и продолжаться последовательно до наибольшей представляющей интерес частоты, или наоборот, продолжаться последовательно от наибольшей представляющей интерес частоты до наименьшей представляющей интерес частоты. На этапе 310 процесс возвращают с этапа 408 на фиг. 4, в случае необходимости выбора другой глубины z. На этапе 311 выбирается глубина z из множества глубин z, выбранных на этапе 302. Выбор глубины производится систематическим образом, соответствующим экстраполяции в нижнее полупространство. Таким образом, выбор глубины производится, начиная с верхнего уровня глубины для массива сейсмических данных, выбранного на этапе 301, и последовательно продолжается вниз. На этапе 312 процесс возвращают с этапа 406 на фиг. 4, в случае необходимости выбора другой субобласти D. На этапе 313 выбирают субобласть D на глубине z, выбранной на этапе 311 из субобластей, выбранных на этапе 303. Выбор субобластей D следует делать систематизированным образом для повышения вычислительной эффективности, хотя систематизированный выбор субобластей D не является требованием изобретения. Например, выбор субобластей D может начинаться с одной стороны глубинного интервала, представленного глубиной z, и продолжаться последовательно до другой стороны. На этапе 314 процесс переходит на этап 401 на фиг. 4. На фиг. 4 показана блок-схема, иллюстрирующая окончательные этапы обработки, в которой используются таблицы прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора, продолжающейся с фиг. 3. На этапе 401 процесс продолжают с этапа 314 на фиг. 3. На этапе 402 вычисляют наибольшее волновое число kmax(D, z) для субобласти D, выбранной на этапе 313 на фиг. 3. Наибольшее волновое число kmax(D, z) вычисляется для частоты , выбранной на этапе 309 на фиг. 3 с использованием наименьшей скорости cmin(D, z), определнной на этапе 305 на фиг. 3. Вычисление наибольшего волнового числа kmax(D, z) следует производить делением частотына наименьшую скорость cmin(D, z), в соответствии с уравнением (14). На этапе 403 выбирают максимальную длину оператора для субобласти, выбранной на этапе 313 на фиг. 3. Максимальная длина оператора выбирается на основе наибольшего волнового числа kmax(D, z),вычисленного на этапе 402. В 2D случае длину оператора следует выбирать как полудлину L(k), соответствующую наибольшему волновому числу kmaxD, z). В 3D случае длину оператора следует выбирать как пару полудлин L(kmax(D, z и М(kmax(D, z, соответствующих наибольшему волновому числуkmax(D, z). На этапе 404 прямую глубинную экстраполяцию применяют в субобласти, выбранной на этапе 313 на фиг. 3. Прямые глубинные операторы выбирают из таблицы прямых глубинных операторов с динами- 10007939 чески переменной длиной оператора, выбранных на этапе 306 на фиг. 3. Прямые глубинные экстраполяционные операторы выбирают таким образом, чтобы их длина не превышала максимальную длину оператора, выбранную на этапе 403. На этапе 405 определяют, остаются ли какие-либо представляющие интерес субобласти D внутри глубины z, выбранной на этапе 311 на фиг. 3. Если ответ положительный, то представляющая интерес субобласть D сохраняется, тогда процесс продолжают на этапе 406 для выбора другой субобласти D. Если ответ отрицательный, и не остатся представляющей интерес субобласти D, тогда процесс продолжают на этапе 407 для проверки глубины z. На этапе 406 процесс возвращают к этапу 312 на фиг. 3 для выбора другой субобласти D. На этапе 407 определяют, остаются ли какие либо представляющие интерес глубины z внутри массива сейсмических данных, выбранного на этапе 307 на фиг. 3. Если ответ положительный, то представляющая интерес глубина z остатся, тогда процесс продолжают на этапе 408 для выбора другой глубиныz. Если ответ отрицательный, и не остатся представляющей интерес глубины z, тогда процесс продолжают на этапе 409 для проверки частот . На этапе 408 процесс возвращают на этап 310 на фиг. 3 для выбора другой глубины z. На этапе 409 определяют, остаются ли какие-либо представляющие интерес частотыдля субобласти D, выбранной на этапе 312 на фиг. 3. Если ответ положительный, то представляющая интерес частотаостатся, тогда процесс продолжают на этапе 410 для выбора другой частоты . Если ответ отрицательный, и не остатся представляющей интерес частоты , тогда процесс продолжают на этапе 411 для завершения. На этапе 410 процесс возвращают на этап 308 на фиг. 3 для выбора другой частоты . На этапе 411 процесс обработки заканчивают. Данное изобретение используется для 2D- и 3D-глубинной экстраполяции, выполняемой с помощью таблиц с оптимизированными в пространственно-частотной области операторами. Эффективное число коэффициентов экстраполяционного оператора изменяется динамически как функция максимального отношения частоты к скорости распространения на некотором уровне глубины или, альтернативно,внутри субобласти на этом уровне глубины. Использование данного изобретения повышает вычислительную эффективность для прямых экстраполяционных схем при одновременном сохранении точности и стабильности. Следует понимать, что вышеизложенное является лишь детальным описанием конкретного варианта реализации изобретения и что многочисленные изменения, модификации и альтернативы приведенным вариантам могут быть сделаны, в соответствии с раскрытым здесь описанием, без выхода за рамки изобретения. Предшествующее описание ограничивает область применения изобретения. Соответственно, рамки изобретения должны определяться только признаками формулы и их эквивалентами. ФОРМУЛА И 3 ОБРЕТЕНИЯ 1. Способ обработки сейсмических данных, включающий создание прямых глубинных экстраполяционных операторов с переменными длинами оператора, зависящими от максимального угла наклона,требования к точности и волнового числа; создание операторных таблиц с использованием прямого глубинного экстраполяционного оператора, имеющего наименьшую длину оператора, удовлетворяющую требованию к точности при максимальном угле наклона для каждого из множества волновых чисел; и выполнение глубинной миграции с использованием прямого глубинного экстраполяционного оператора в субобласти на некоторой глубине, имеющего наименьшую длину оператора из операторных таблиц для наибольшего волнового числа в указанной субобласти на указанной глубине. 2. Способ по п.1, отличающийся тем, что этап создания операторных таблиц включает в себя выбор максимального угла наклона; выбор типа оператора; выбор требования к точности для указанного типа оператора; выбор множества волновых чисел и выполнение следующих этапов для каждого из множества волновых чисел: выбор множества длин оператора для выбранного волнового числа и выполнение следующих этапов для каждой из множества длин оператора: определение, удовлетворяет ли выбранный тип оператора с выбранной длиной оператора выбранному требованию к точности при выбранном максимальном угле наклона и выбранном волновом числе; определение, является ли длина оператора наименьшей длиной оператора, удовлетворяющей требованию к точности при выбранном максимальном угле наклона для выбранного волнового числа, и запоминание длины оператора в операторной таблице, если длина оператора является наименьшей длиной оператора, удовлетворяющей требованию к точности при максимальном угле наклона для выбранного волнового числа. 3. Способ по п.2, отличающийся тем, что этапы, которые выполняют для каждого волнового числа,включают выбор множества пар первых полудлин оператора и вторых полудлин оператора для выбранного волнового числа; и выполнение следующих этапов для каждой из множества пар первых полудлин- 11007939 оператора и вторых полудлин оператора: определение, удовлетворяет ли выбранный тип оператора с выбранной парой из первой полудлины оператора и второй полудлины оператора выбранному требованию к точности при выбранном максимальном угле и выбранном волновом числе; определение, является ли первая полудлина оператора наименьшей первой полудлиной оператора,удовлетворяющей требованию к точности для выбранного волнового числа, и является ли вторая полудлина оператора наименьшей второй полудлиной оператора, удовлетворяющей требованию к точности для выбранного волнового числа; и запоминание пары из первой полудлины оператора и второй полудлины оператора в операторной таблице, если первая полудлина оператора является наименьшей первой полудлиной оператора, удовлетворяющей требованию к точности для выбранного волнового числа, и если вторая полудлина оператора является наименьшей второй полудлиной оператора, удовлетворяющей требованию к точности при выбранном максимальном угле наклона для выбранного волнового числа. 4. Способ по п.1, отличающийся тем, что этап создания операторных таблиц включает в себя выбор максимального угла наклона; выбор типа оператора; выбор требования к точности для указанного типа оператора; вычисление предварительных операторных таблиц для переменных длин оператора; выбор множества волновых чисел и выполнение следующих этапов для каждого из множества волновых чисел: выбор наименьшей длины оператора в предварительных операторных таблицах, удовлетворяющей требованию к точности для выбранного волнового числа; и запоминание наименьшей длины оператора в операторной таблице. 5. Способ по п.4, отличающийся тем, что этапы, которые выполняют для каждого волнового числа,включают в себя выбор пары из наименьшей первой полудлины оператора и наименьшей второй полудлины оператора в предварительных операторных таблицах, удовлетворяющей требованию к точности для выбранного волнового числа; и запоминание пары из наименьшей первой полудлины оператора и наименьшей второй полудлины оператора в операторной таблице. 6. Способ по п.1, отличающийся тем, что этап выполнения глубинной миграции включает в себя выбор массива сейсмических данных; выбор диапазона глубин в массиве сейсмических данных; выбор субобласти для каждого значения глубины из выбранного диапазона глубин; определение скоростной модели для указанного массива сейсмических данных и диапазона глубин; определение наименьшей скорости в каждой субобласти на скоростной модели; выбор операторной таблицы с переменными длинами оператора; выбор множества частот в выбранной субобласти и выполнение следующих этапов для каждой из множества частот, для каждого значения глубины из выбранного диапазона глубин и для каждой субобласти на данной глубине: вычисление наибольшего волнового числа в субобласти по частоте и наименьшей скорости в этой субобласти; выбор максимальной длины оператора из операторной таблицы для вычисления наибольшего волнового числа; применение операторов из операторной таблицы с длинами оператора, не превышающими максимальную длину оператора в выбранной субобласти. 7. Способ по п.6, отличающийся тем, что операторная таблица с переменными длинами оператора включают прямые экстраполяционные операторы с переменными длинами оператора. 8. Способ по п.6, отличающийся тем, что этап выбора операторной таблицы с переменными длинами оператора дополнительно включает интерполяцию операторной таблицы с переменными длинами оператора. 9. Способ по п.6, отличающийся тем, что длина каждого оператора включает пару из первой полудлины оператора и второй полудлины оператора. 10. Способ по п.2, отличающийся тем, что этап выбора типа оператора включает применение следующей формулы: где Р(хi, уj, , z+z) является сейсмическим волновым полем в точке с горизонтальными координатами хi=iх, уj=jу и глубиной z+z;является угловой частотой; Р(хi, уj, , z) является сейсмическим волновым полем в субобласти D на глубине z; х, у и z являются длинами шагов в направлении х-, у- и zкоординат соответственно; L(kmax(D, z и M(kmax(D, z являются полудлинами оператора в направле- 12007939 нии х- и у-координат соответственно, для наибольшего волнового числа kmax(D, z) в субобласти D на глубине z; W(xi, уj, k(xi, yj, z), z) является прямым глубинным экстраполяционным оператором; и k(хi,уj, z) является локальным волновым числом. 11. Способ по п.10, отличающийся тем, что волновое число k(хi, yj, z) задают формулой где с(хi, yj, z) является локальной скоростью распространения. 12. Способ по п.10, отличающийся тем, что наибольшее волновое число kmax(D, z) для частотыв субобласти D на глубине z задают формулой где cmin(D, z) является наименьшей скоростью в субобласти D на глубине z. 13. Способ по п.2, отличающийся тем, что этап выбора типа оператора включает применение следующей формулы: где Р(хi, , z+z) является сейсмическим волновым полем в точке с горизонтальной координатой хi=iх и глубиной z+z;является угловой частотой; P(xi, , z) является сейсмическим волновым полем в субобласти D на глубине z; х и z являются длинами шагов в направлении х- и z-координат соответственно; L(kmax(D, z является полудлиной оператора для наибольшего волнового числа kmax(D, z) в субобласти D на глубине z в направлении х-координаты; W(xi, k(хi, z), z) является прямым глубинным экстраполяционным оператором; и k(хi, z) является локальным волновым числом. 14. Способ по п.13, отличающийся тем, что волновое число k(хi, z) задают формулой где c(xi, z) является локальной скоростью распространения. 15. Способ по п.2, отличающийся тем, что этап выбора типа оператора включает применение следующей формулы: где P(xi, yj, , z+z) является сейсмическим волновым полем в точке с горизонтальными координатами хi=iх, уj =jу и глубиной z+z;является угловой частотой; Р(хi, уj, , z) является сейсмическим волновым полем в субобласти D на глубине z; х, у и z являются длинами шагов в направлении х-, у- и zкоординат соответственно; L(kmax(D, z является длиной оператора для наибольшего волнового числаkmax(D, z) в субобласти D на глубине z; Wl(k(xi, yj, z), z) является прямым глубинным экстраполяционным оператором, выраженным в цилиндрических координатах; k(хi, уj, z) является локальным волновым числом; и hl(xi, yj, , z) являются вспомогательными полями, полученными в результате применения рекурсивных 2D-фильтров Чебышева к сейсмическому волновому полю P(xi, уj, , z).
МПК / Метки
МПК: G06F 19/00, G01V 1/28
Метки: операторов, экстраполяционных, способ, основе, переменной, глубинных, использования, динамически, миграции, длиной, сейсмической, оператора, прямых
Код ссылки
<a href="https://eas.patents.su/16-7939-sposob-sejjsmicheskojj-migracii-na-osnove-ispolzovaniya-pryamyh-glubinnyh-ekstrapolyacionnyh-operatorov-s-dinamicheski-peremennojj-dlinojj-operatora.html" rel="bookmark" title="База патентов Евразийского Союза">Способ сейсмической миграции на основе использования прямых глубинных экстраполяционных операторов с динамически переменной длиной оператора</a>