Способ применения метода фильтра калмана для обработки электромагнитных данных

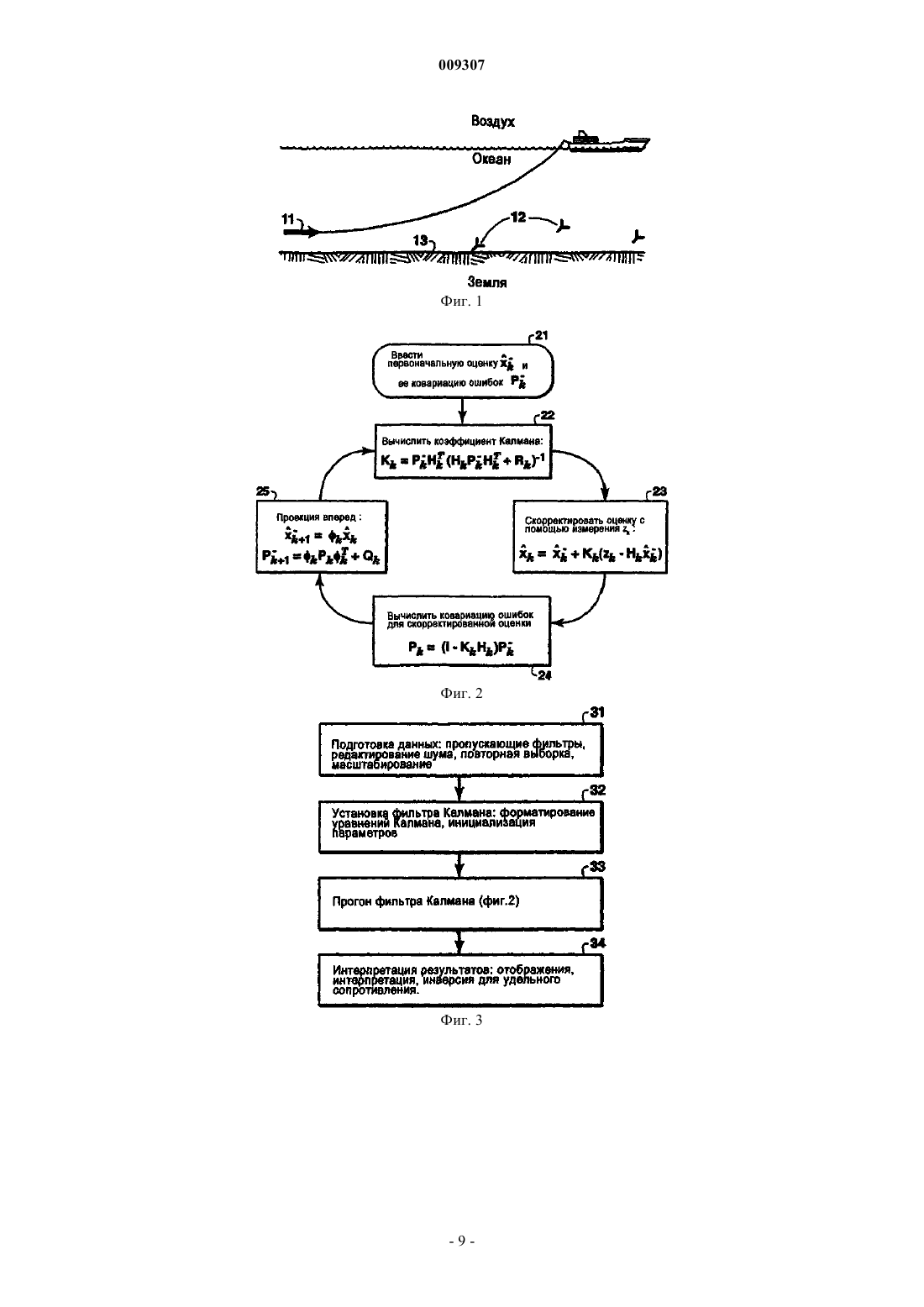
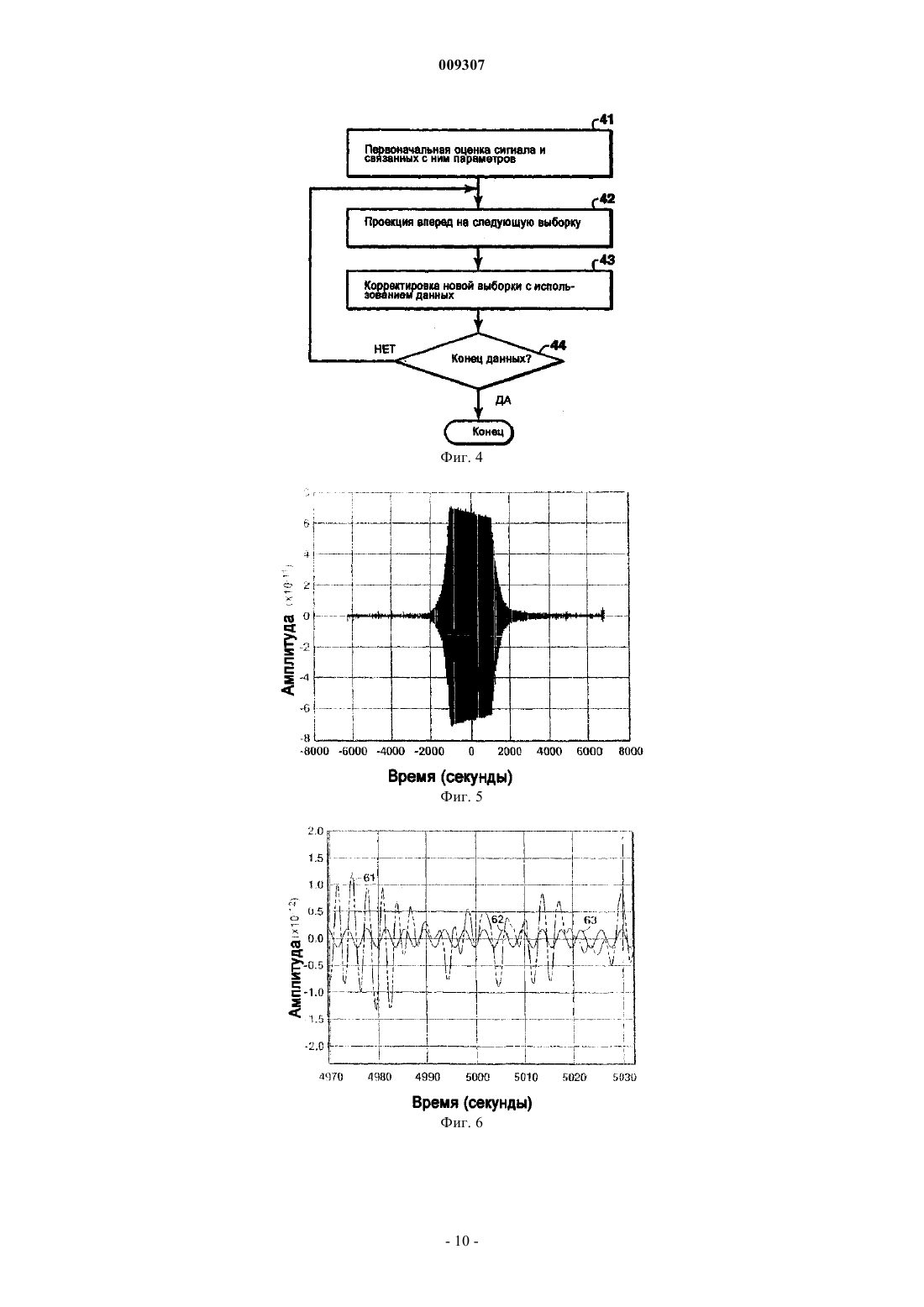
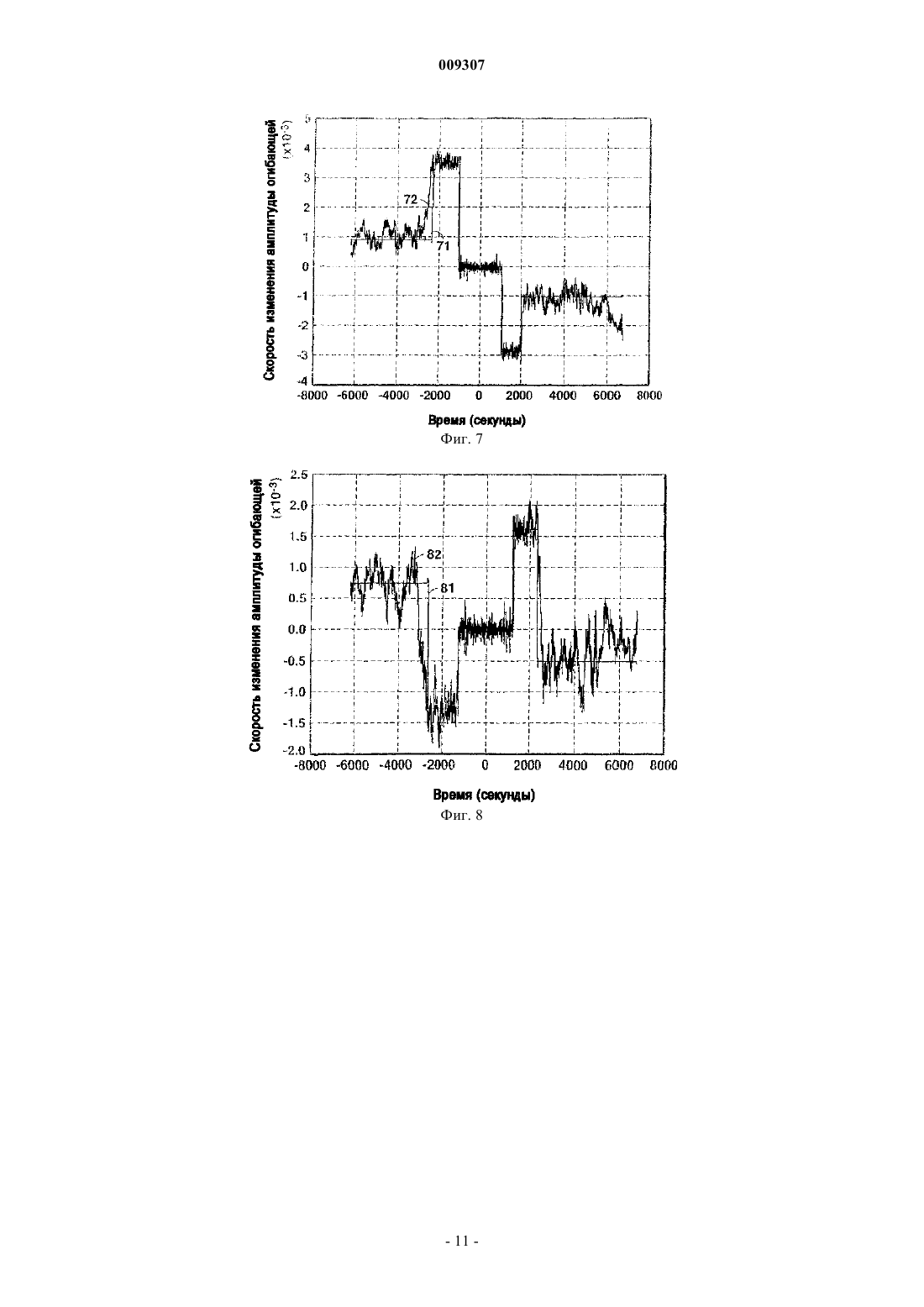
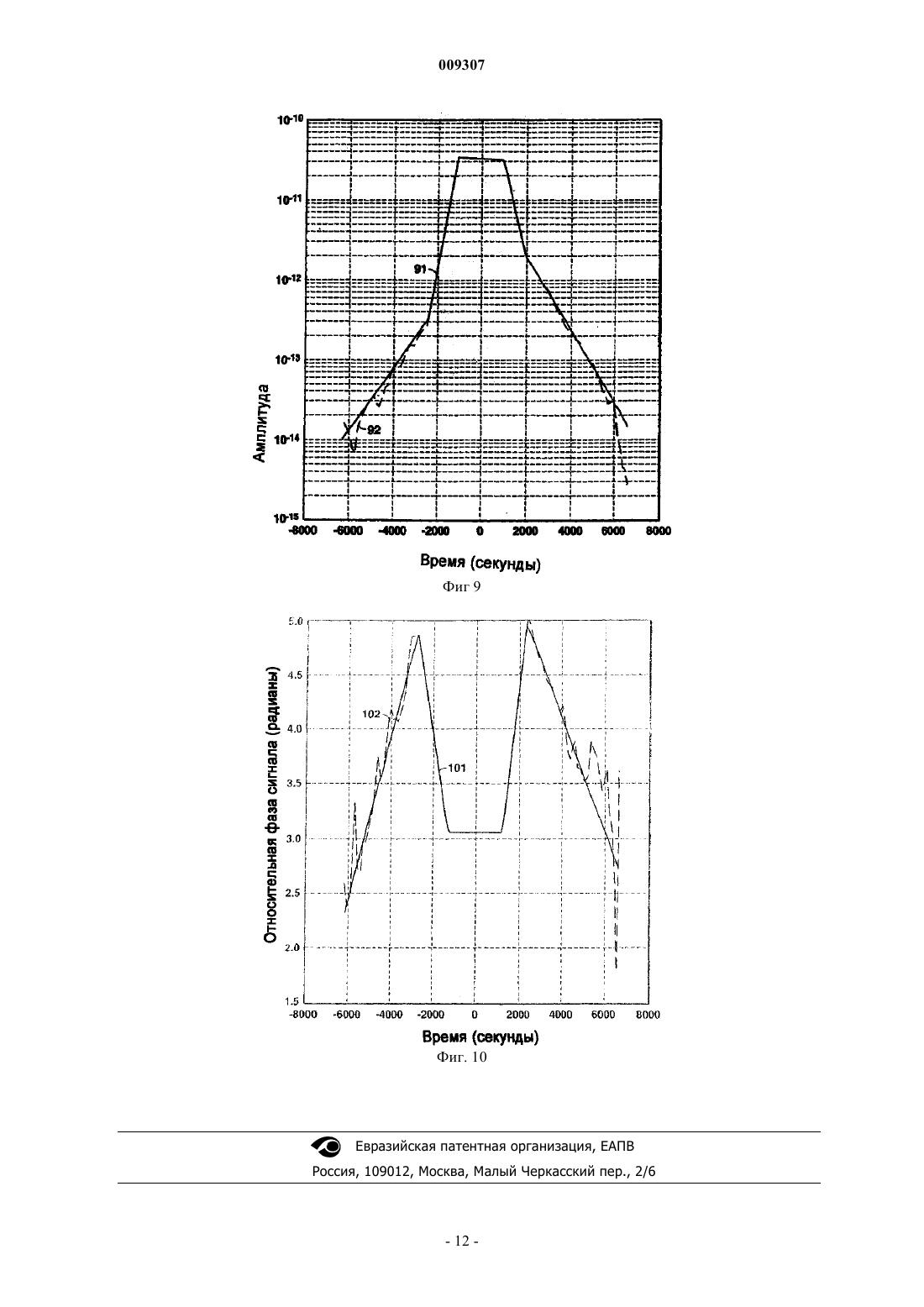
009307 Приоритет настоящей заявки заявлен на основании предварительной заявки на патент США 60/576201, поданной 1 июня 2004 г. Область техники Настоящее изобретение относится, в общем, к области геофизической разведки и, более конкретно,к электромагнитным способам, используемым для разведки углеводородов. В частности, предложен способ отслеживания электромагнитных сигналов источников, используемых в электромагнитном методе разведки с управляемым источником, который позволяет восстанавливать сигнал из шума. Описание известного уровня техники В геофизической разведке на основе электромагнитного способа исследований с управляемым источником (CSEM) используются активные (искусственные) источники для создания электромагнитных полей для возбуждения земли, а также приемные устройства, которые размещаются на поверхности земли, на морском дне или внутри скважин для измерения результирующих электрических и магнитных полей, т.е. реакции земли на возбуждение данным источником. На фиг. 1 показаны основные элементы морской разведки методом CSEM. Судно буксирует погруженный передатчик CSEM 11 по участку морского дна 13. Затем измеренные приемниками 12 электрические и магнитные поля анализируются для определения удельного сопротивления земных структур (подземных формаций) под поверхностью или морским дном. Этот метод применяется в береговой разведке минералов, тектонических исследованиях океана и морской разведке ресурсов нефти и минералов. Сигналы активного электромагнитного источника можно рассматривать как сумму синусоидальных сигналов (например, прямоугольного сигнала, состоящего из частоты основной гармоники и нечетных гармоник). Примером такого источника является горизонтальный электрический диполь, используемый во многих операциях CSEM. При увеличении сдвига, т.е. расстояния между таким дипольным источником 11 и приемниками 12, синусоидальный сигнал может претерпевать значительное затухание. Кроме того, сдвиги на расстоянии часто имеют критическое значение для определения удельного сопротивления представляющих интерес структур, находящихся на большой глубине. Поэтому существует потребность в обеспечении наилучшего возможного отношения сигнал-шум для этого синусоидального сигнала. Традиционные способы обработки для улучшения отношения сигнал-шум таких электромагнитных(ЭМ) данных включают в себя разбивку данных на временные окна, на которых применяется анализ Фурье или подобный метод для вычисления амплитуды и фазы выбранной частотной составляющей(их). См. например, Constable and Cox, "Marine controlled-source electromagnetic sounding 2 (Морское электромагнитное зондирование с управляемым источником). The PEGASUS Experiment", Journal of GeophysicalResearch 101, 5519-5530 (1996). Эти окна не могут быть слишком большими, так как амплитуда и относительная фаза сигнала могут существенно изменяться в пределах аналитического окна. Однако маленькие окна позволяют обеспечить только минимальное улучшение отношения сигнал-шум. В известных способах требуется находить компромисс между этими двумя крайностями. Другой проблемой известных способов является то, что в них не используются корреляции между сигналом и шумом. В частности, существенную проблему для ЭМ отображения активного морского источника представляют низкочастотные магнитотеллурические (МТ) шумы, потому что они могут маскироваться под сигнал, (магнитотеллурический (МТ) шум - это электромагнитные излучения от природных неактивных источников). Можно использовать корреляции между различными детекторами для облегчения отделения сигналов активных источников от этих шумов. Другие корреляции между сигналом и шумом (например, корреляции сигналов на двух горизонтальных составляющих) не находят оптимального применения в известных методах. Алгоритм фильтра Калмана был создан для решения проблем навигационного позиционирования, и он особенно хорошо подходит для категории проблем отслеживания (Калман, 1960). После первой публикации Калмана в Trans.of.the ASME-J.of Basic Engr., 35-45(1960) было опубликовано много работ, посвященных модификациям и применениям базового фильтра Калмана, например в монографии Брауна(Brown) в Introduction to Random Signal Analysis and Kalman Filtering (Введение в анализ случайных сигналов и фильтрацию Калмана), John WileySons, N.Y. (1983). Некоторые из этих модификаций имеют значение для некоторых вариантов осуществления настоящего изобретения. Стандартный фильтр Калмана работает в одном направлении и фильтрует данные в последовательности этого направления (или времени). Поэтому на результат фильтра влияют только предшествующие данные. В работах Rauch et al. (далее Раух) была предложена важная модификация, обеспечивающая оптимальное решение с использованием всей регистрации времени (Rauch, "Solutions to the linear smoothingRauch, et al., "Maximum likelihood estimates of linear dynamic systems" (Оценки максимального правдоподобия линейных динамических систем), AIAA J.3, 1445 (1965). В работе Szelag (далее Шелаг) предложена другая алгоритмическая модификация, которая позволяет фильтру отслеживать синусоидальные сигналы известной частоты, см. "A short term forecasting algorithm for trunk demand servicing" (Алгоритм краткосрочного прогнозирования для удовлетворения потребностей телефонных линий), The Bell SystemTechnical Journal 61, 67-96(1982). Это решение было разработано для отслеживания годовых циклов значений нагрузки телефонных линий. На фиг. 2 представлена последовательность процесса, иллюстрирующая алгоритм Калмана. Более подробно см. монографию Брауна, стр.200. В работе La Scala, et al. описано использование известного расширенного фильтра Калмана для отслеживания изменяющейся во времени частоты ("Design of an extended Kalman filter frequency tracker"(Конструкция блока отслеживания частоты на основе расширенного фильтра Калмана), IEEE Transactionson Signal Processing 44, No.3, 739-742(Mar.,1966). В этой работе используется предположение, что амплитуда сигнала остается постоянной. Следовательно, конкретный используемый алгоритм Калмана нацелен на отслеживание сигнала неизвестной частоты, причем эта частота может претерпевать значительные изменения. Lagunas, et al. описывают расширенный фильтр Калмана для отслеживания сложных синусоид в присутствии шума и изменений частоты, например, доплеровских сдвигов. (High Order Learning inTemporal Reference Array Beamforming", Signal Proc.VI, Theories and Applications, Elsevier Sci.Pub.В.V.,pp.1085-1088(1992). Подобно способу La Scala, алгоритм Lagunas предназначен для отслеживания синусоид неизвестной частоты. Поэтому оба метода недостаточно оптимальны для отслеживания сигнала с постоянной или почти постоянной частотой. Метод Lagunas также позволяет отслеживать изменения амплитуды, если они относительно небольшие. Однако ни одно из известных изобретений не направлено на обработку данных электромагнитной разведки с использованием электромагнитного источника, передающего известные сигналы с известной частотой. Поэтому существует потребность в способе отслеживания больших изменений амплитуды и небольших изменений фазы относительно известной синусоиды с использованием больших окон или даже всех электромагнитных данных. Настоящее изобретение позволяет удовлетворить эту потребность. Краткое изложение сущности изобретения Согласно одному варианту осуществления изобретения предложен способ отслеживания изменений амплитуды и фазы передаваемого периодического электромагнитного сигнала в зашумленных данных,обнаруживаемого в течение времени по меньшей мере одним приемником, причем данный сигнал передают с известной частотой, заключающийся в том, что (а) выбирают алгоритм отслеживания для отслеживания сигнала известной частоты; (b) разделяют время обнаружения на интервалы, в течение каждого из которых обнаруживаемый сигнал и по меньшей мере один связанный с ним параметр предположительно не изменяются; (с) оценивают первоначальные значения для обнаруженного сигнала и по меньшей мере одного связанного с ним параметра и присваивают эти значения первому интервалу времени;(d) оценивают проекцию первоначального сигнала и каждого связанного с ним параметра на один интервал времени вперед; (е) корректируют первоначальные оценки этапа (d), используя упомянутые данные и алгоритм отслеживания; и (f) повторяют этапы (d)-(e) до тех пор, пока не будут обработаны все данные. В некоторых вариантах осуществления изобретения алгоритм отслеживания является алгоритмом Калмана, включающим в себя вектор состояния, определенный уравнением состояния и уравнением измерений. В некоторых из этих вариантов вектор состояния имеет две составляющие - амплитуду сигнала и квадратурный сигнал. В других вариантах осуществления изобретения, особенно полезных для ситуаций, в которых сигнал претерпевает большие затухания, вектор состояния имеет две дополнительные составляющие, которые можно использовать для облегчения отслеживания сигнала: скорость изменения амплитуды огибающей сигнала и скорость изменения относительной фазы сигнала. Краткое описание чертежей Далее настоящее изобретение и его преимущества будут описаны более подробно со ссылками на прилагаемые чертежи, на которых фиг. 1 иллюстрирует схему осуществления обычной электромагнитной разведки с управляемым источником в полевых условиях; фиг. 2 изображает последовательность осуществления основных этапов алгоритма Калмана; фиг. 3 изображает алгоритм осуществления основных этапов одного варианта осуществления способа согласно настоящему изобретению с применением фильтра Калмана в качестве алгоритма отслеживания; фиг. 4 изображает алгоритм осуществления более общего варианта согласно настоящему изобретению и фиг. 5-10 изображают результаты предложенного способа с применением алгоритма Калмана для моделирования данных с частотой сигнала 0,25 Гц и аддитивным случайным шумом. Изобретение будет описано в связи с его предпочтительными вариантами осуществления. Однако,поскольку следующее подробное описание является специфическим для конкретного варианта или конкретного использования изобретения, оно является всего лишь иллюстративным и не ограничивает объем изобретения. Напротив, изобретение охватывает все альтернативы, модификации и эквиваленты, которые могут быть подпадать под объем притязаний изобретения, охарактеризованный в прилагаемой формуле изобретения. Подробное описание предпочтительных вариантов Предложен способ использования фильтра отслеживания, такого как алгоритм Калмана, для отсле-2 009307 живания синусоидального сигнала и восстановления этого сигнала из электромагнитного шума. Предлагаемый способ применения фильтра Калмана позволяет решить проблемы описанных выше известных принципов. Прежде всего, для получения оценки в каждый момент может быть использована большая часть зарегистрированных данных. Это важно, поскольку электромагнитные данные могут быть высоко коррелированны в течение длительных периодов времени благодаря низкой скорости изменений фазы относительно эталонной синусоидальной волны. Иными словами, информация в конкретное время дает информацию о сигнале, который будет гораздо позже. С другой стороны, в анализе Фурье на изолированных временных окнах не используется никакой информации за пределами текущего окна. В частности, рассчитанные амплитуды и фазы могут иметь прерывистый характер между окнами. Метод Калмана может также включать в себя такие характеристики сигнала и шума, как корреляции шума между удаленными детекторами (или различными компонентами одного и того же детектора), корреляции сигналов между компонентами, изменения амплитуды изменяющегося во времени сигнала и шума, и прогнозируемые влияния геологии на данные. Чтобы можно было применить фильтр Калмана, процесс необходимо выразить через два линейных уравнения: уравнение состояния и уравнение измерений. В случаях, которые удовлетворяют это предположение, алгоритм Калмана дает оптимальную оценку сигнала методом наименьших квадратов вместе с соответствующей ковариацией ошибок. Это предположение о линейности будет действительным для большинства применений. Оно может не работать в тех случаях, когда шум измерений не является аддитивным, например при некоторых видах ограничения или искажения сигнала или мультипликативном шуме. Аналогичным образом, уравнение состояния может не соответствовать предположению о линейности, если, например, сигнал совершенно непредсказуем от одной выборки к другой или если система практически нестабильна, когда размер сигнала влияет на матрицу перехода. Однако ситуации, имеющие умеренную нелинейность, можно все же моделировать, используя расширения или другие аппроксимации, как это делается ниже. Требуемое уравнение состояния содержит вектор состояния xk который можно установить несколькими путями для обработки электромагнитных данных. Вектор xk будет содержать, как минимум, две составляющие. Они включают в себя сигнал (например, горизонтальное электрическое поле в конкретном местоположении) и соответствующий ему квадратурный сигнал. Квадратура - это сигнал после поворота фазы на 90. Для синусоидальных сигналов квадратура пропорциональна производной сигнала. Две составляющие необходимы потому, что синусоида это решение дифференциального уравнения второго порядка. Для оценивания каждого сигнала в каждом положении детектора требуются дополнительные пары составляющих. Для каждого рассчитанного сигнала можно также при необходимости смоделировать дополнительные производные. Эти дополнительные производные полезны потому, что обновления производной дают более гладкую коррекцию оценки сигнала. Фильтр Калмана требует определения матриц ковариации шумов и ковариации энергии сигнала. Вводы ковариации шумов можно использовать, например, для индикации уровня шума и корреляций,обусловленных МТ шумом. Вводы ковариации энергии сигнала показывают необходимую степень регулировки фильтра и любую корреляцию сигналов между компонентами. После определения параметров фильтра можно предварительно обработать данные, прежде чем приступать к выполнению алгоритма фильтра. Для начала данные можно масштабировать таким образом, чтобы ожидаемая часть сигнала данных имела относительно плоскую амплитуду. Иными словами,сдвиги на расстоянии масштабируются с повышением, используя грубый прогноз скорости затухания сигнала со сдвигом. Алгоритм фильтра должен только отслеживать изменения этой ожидаемой скорости затухания, что можно реализовать гораздо проще, чем отслеживать быстрое затухание амплитуды со сдвигом. При масштабировании с повышением этих данных для уравновешивания сигнала случайный шум будет также масштабироваться с повышением. Это можно задать в матрице ковариации шумов,чтобы в алгоритме учитывалось, что данные со сдвигом на расстоянии содержат больше шума. В других вариантах предложенного способа большие изменения амплитуды обрабатываются путем моделирования скоростей затухания амплитуды вместо самих амплитуд. Скорости затухания (или подъема) могут иметь подобную амплитуду, даже если сам сигнал изменяется на несколько порядков величины. Можно также идентифицировать всплески шумов или отсутствующие данные, чтобы фильтр переносил синусоиду через эти зоны, не требуя данных. Можно также корректировать шум измерений, чтобы он соответствовал требованию белого шума. Эти корректировки могут включать в себя компенсирующие фильтры, методы подавления постоянной составляющей, фильтры для удаления гармонического шума(если его не рассматривать как сигнал) и моделирование окрашенного шума с использованием отдельной переменной(ых) состояния. У типичного прямоугольного сигнала кроме номинальной основной частоты имеются нечетные гармоники. Эти гармоники можно отфильтровывать (используя пропускающие фильтры) и обрабатывать как отдельные сигналы, или же их можно моделировать одновременно с основными гармониками. Одновременное моделирование имеет смысл, если ожидается, что корректировки гармонического сигнала будут коррелировать с корректировками основного сигнала.-3 009307 После описания модели и предварительной обработки можно использовать алгоритм фильтра Калмана для оценки составляющих вектора состояния как функции времени и соответствующих строк сообщений об ошибках вычисления. Затем можно использовать эту оптимальную оценку в дальнейшей электромагнитной интерпретации путем сравнения с параметрическими моделями или путем использования ее в качестве ввода в инверсию для структуры удельного сопротивления, как предложено в патенте США 6603313 (Srnka). На фиг. 3 показаны основные этапы осуществления одного варианта настоящего изобретения. В этом варианте осуществления изобретения фильтр Калмана отслеживает изменения амплитуды и фазы принимаемого электромагнитного сигнала как функцию времени. В следующем обсуждении предполагается, что источник и/или приемник движутся и поэтому сдвиг между источником и приемником изменяется как функция времени (как на фиг. 1, где изображен движущийся источник). Настоящее изобретение в равной мере подходит и для неподвижного источника и приемников, хотя этот способ и не является эффективным для проведения разведки CSEM. Увеличения сдвига между источником и приемником приводят к существенному ослаблению принимаемого сигнала. Это представляет потенциальную проблему для алгоритма отслеживания, так как ожидаемый сигнал и его корректировки могут изменяться на несколько порядков величины. На этапе 31 на фиг. 3 выполняются определенные предварительные операции для подготовки данных, измеренных приемниками. Одна такая операция направлена на решение проблемы широкого изменения сигнала в пределах сдвига, используемых в разведке. Существует два пути решения этой проблемы. При одном подходе данные можно предварительно масштабировать для компенсирования типичных скоростей понижения амплитуды со сдвигом. Для определения этого затухания амплитуды необходимо обратиться к результатам модели, охватывающим диапазон ожидаемых проводимостей. После масштабирования задача фильтра упрощается, так как он только отслеживает отклонения от этого основного случая, и размер корректировок остается относительно постоянным. При альтернативном подходе к проблеме изменения амплитуды вводятся переменные состояния,которые соответствуют скорости изменения амплитуды и фазы. Эти скорости легче моделировать, так как они имеют относительно постоянные значения для амплитуд, затухающих или возрастающих экспоненциально. Можно также предусмотреть и другие подходы к проблеме амплитуды, включая даже отсутствие каких-либо действий в отношении изменения амплитуды, и все они подпадают под объем изобретения. На этапе 31 также предпочтительно определяется ожидаемый шум в матрице ковариации шумов(обсуждающейся ниже), чтобы алгоритм мог оптимально использовать различные количества данных. Например, могут иметь место случайные всплески шума (краткие шумы с высокой амплитудой). Их можно отметить флажками при предварительной обработке, чтобы фильтр Калмана переносил синусоиды сигнала через эти зоны без использования этих данных. Другая желательная операция предварительной обработки включает в себя фильтрацию частоты для балансировки шумового спектра, для обеспечения точности предположения белого аддитивного шума. Для этого обычно выполняют понижающее масштабирование очень низкочастотных составляющих(например, ниже частоты основного сигнала), так как МТ шум окружающей среды обычно самый большой на этих частотах. Кроме того, можно отфильтровать нижние частоты данных для удаления более высокочастотных шумов и позволить сделать повторную выборку с интервалом большего размера. Повторная выборка улучшает вычислительные требования алгоритма. Типичный прямоугольный сигнал источника будет включать в себя нечетные гармоники в дополнение к номинальной основной частоте. Эти гармоники можно отфильтровать (используя пропускающий или узкополосный режекторный фильтр) и обрабатывать их как отдельные сигналы, или же их можно моделировать одновременно с основными гармониками. Одновременное моделирование может быть предпочтительным, если ожидается, что корректировка гармонического сигнала будет коррелировать с корректировками основного сигнала. В завершение описания этапа 31 следует отметить, что в предпочтительных вариантах изобретения используется несколько методов подготовки данных, включая описанные выше, однако ни один из них не имеет критического значения для изобретения. На этапе 32, показанном на фиг. 3, устанавливают фильтр Калмана для применения. В других вариантах осуществления изобретения можно использовать другие алгоритмы слежения вместо фильтра Калмана. На фиг. 4 показаны основные этапы, которые выполняются в таком более общем варианте осуществления изобретения. На этапе 41 в алгоритм вводятся первоначальные оценки сигнала и связанные с ними параметры. Обычно эти первоначальные значения временных выборок будут включать в себя представляющий интерес сигнал и его производную. Эти первоначальные значения можно определить из данных с близким сдвигом, имеющих высокое отношение сигнал-шум. Альтернативно можно использовать произвольное первоначальное предположение с расчетом на то, что алгоритм быстро сойдется с правильными значениями. На этапе 42 эти первоначальные значения проецируются на одну выборку вперед, используя, например, матрицу вращения, которая будет обсуждаться ниже в связи с фильтром-4 009307 Калмана. На этапе 43 новую выборку корректируют на основании измеренных данных и специфики конкретного алгоритма слежения. На этапе 44 завершается один цикл программы, который повторяется до тех пор, пока не закончатся данные, т.е. пока сигнал не будет спроецирован вперед на тот интервал времени, для которого собирались данные. Краткость этого объяснения обусловлена тем, что другие детали,описанные ниже в связи с фильтром Калмана, также применимы к общему алгоритму. Фильтр Калмана является предпочтительным решением для формулировки пространства состояния для проблемы отслеживания электромагнитного сигнала. Эта формулировка имеет два матричных уравнения: уравнение "состояния" и уравнение "измерений". Уравнение состояния выражается как где xk - вектор состояния в выборке k, Фk - матрица перехода состояния и wk - вынуждающая функция состояния. Шкала времени разделена на конечные интервалы, и измерение каждым приемником преобразуется в одно число (обозначенное zk в уравнении измерений ниже) для каждого интервала времени. Выборка данных к относится к оцифрованному выводу для k-того интервала времени, где k - целочисленный индекс, обозначающий последовательные интервалы времени. Вынуждающая функция - это белая последовательность, которая представляет отличия в следующей выборке вектора состояния, от того, что в противном случае было бы спрогнозировано матрицей перехода, примененной к текущей выборке. Матрица перехода дает прогнозируемый вектор состояния на следующей выборке в отсутствии какого-либо новшества (где wk равно нулю). Метод Шелага был адаптирован для моделирования колеблющегося сигнала. Шелаг использовал двухэлементный вектор состояния с составляющими для колеблющегося сигнала и его квадратурного сигнала (пропорционального производной). В других вариантах изобретения можно использовать дополнительные составляющие для моделирования других производных сигнала. Для случая с двумя составляющими матрица перехода, которая создает колебание с частотой f, определяется как где f - частота сигнала и T - интервал выборки. В предпочтительном варианте осуществления изобретения эта простая формула расширяется, чтобы можно было вместо этого отслеживать амплитуду и относительную фазу, потому что для типичной проблемы SCEM амплитуда и относительная фаза будут постепенно изменяться со временем (сдвигом). В этой формуле используется вектор состояния с четырьмя составляющими: где xs - колеблющийся сигнал, xq - квадратурный сигнал, А - скорость изменения амплитуды огибающей сигнала, и v - скорость изменения относительной фазы сигнала (т.е. сдвиг частоты). Так как амплитуда и фаза не имеют линейной связи с сигналом, в одном варианте осуществления изобретения применяется небольшая корректирующая линеаризация для уравнения состояния. Поскольку ожидается, что изменения v и А будут небольшими, можно полагать, что предположение о линейности будет действительным. Этот процесс линеаризации начинается с оценки значений xs и xq для выборки (k+1), если в выборкеk даны значения для четырех элементов вектора состояния. Если амплитуда или относительная фаза не изменяются, то простая матрица вращения Ф уравнения (2) дает проекцию значений xs и xq на следующую выборку: В этом варианте осуществления изобретения далее предполагается, что амплитуда (огибающая сигнала) увеличивается со скоростью А в секунду. Иными словами, при переходе к следующей выборке амплитуда умножается на (1+TА). Вот что произойдет с огибающей сигнала, если и xs, и xq будут масштабированы с этим коэффициентом: Далее учитывается небольшое изменение относительной фазы, происходящее со скоростью v радиан/с. Оно вызовет сдвиг фазы на vT при переходе к следующей выборке. Его можно ввести в уравнение состояния путем изменения синусоид вращения уравнений (5) следующим образом: Для линеаризации используется тот факт, что vT1, и уравнение (7) принимает вид Объединение уравнений (6) и (8) с сохранением только корректировок первого порядка дает модифицированное уравнение состояния: где и Следует отметить, что изменения относительно синусоиды постоянной амплитуды происходят только через элементы А и v, так как только при этих элементах wk не равно нулю. Также следует определить ковариационную матрицу, связанную с wk. Она является средством для управления скоростью адаптации фильтра - большая ковариация в wk означает, что требуются боле значительные изменения А и v. Когда моделируется несколько составляющих данных, корреляции сигналов можно показывать недиагональными элементами в ковариационной матрице состояния. Возможны также другие модификации уравнения состояния. Как минимум, xk будет содержать две составляющие. Это будет сигнал (например, горизонтальное электрическое поле в конкретном месте) и его соответствующий квадратурный сигнал (пропорциональный производной). Для моделирования изменений амплитуды и фазы модели используются две дополнительные составляющие. Дополнительные составляющие необходимы для каждого сигнала, оцениваемого в каждом местоположении детектора. При необходимости можно также моделировать дополнительные производные для каждого оцениваемого сигнала. Дополнительные производные могут быть полезны, так как обновления производной дают более гладкую коррекцию оценки сигнала. Уравнение измерений для фильтра Калмана в описанном выше варианте выглядит так где zk - измеренные данные в выборке k, H = [1 0 0 0]' - матрица измерений, которая выбирает xs в векторе состояния, и vk - шум измерений. Алгоритм Калмана хорошо работает для шума, который является белым или приблизительно белым. Если же шум узкополосный, например синусоидальный, его можно смоделировать как отдельную составляющую сигнала и удалить. Соответствующая ковариационная матрица для vk дает ожидаемую дисперсию и корреляцию шума. Дисперсия может быть изменяющейся во времени, например, как при работе с масштабированными данными (т.е. шум будет изменяться экспоненциально для экспоненциально масштабированных данных). Можно также определить особенно зашумленные зоны с более значительными дисперсиями для минимизирования эффектов всплесков шума. Ковариационная матрица vk также является местом, куда можно включить информацию о коррелированном шуме для случая с множеством составляющих. Это может быть полезно, например, когда удаленный детектор содержит информацию о МТ шуме. В заключение обсуждения этапа 32 на фиг. 3 можно отметить, что описанный принцип использования фильтра Калмана позволяет решить проблемы, описанные в разделе Описание известного уровня техники. Прежде всего, он позволяет использовать большое эффективное окно данных для получения оценки в каждый момент времени. Это важно, потому что электромагнитные данные могут быть высоко коррелированными в течение длительных периодов времени, благодаря низкой скорости изменения фазы относительно эталонной синусоидальной волны. Иными словами, информация в конкретное время дает информацию о сигнале, который будет гораздо позже. С другой стороны, в анализе Фурье на изолированных временных окнах не используется никакой информации за пределами текущего окна. В частности, рассчитанные амплитуды и фазы могут быть прерывистыми между окнами. В метод Калмана можно также включить такие характеристики сигнала и шума, как, например, корреляции шумов между удаленными детекторами (или различными компонентами одного и того же детектора), корреляции сигналов между компонентами, изменения амплитуды изменяющегося во времени сигнала и шума и прогнозируемые влияния геологии на данные. На этапе 33, показанном на фиг. 3, уравнение состояния, уравнение измерений и соответствующие-6 009307 ковариационные матрицы используются для применения фильтра Калмана, как было проиллюстрировано на фиг. 2. Фильтр Калмана обычно работает в одном направлении. Существует по меньшей мере два пути использования информации, опережающей текущую выборку, т.е. данных, измеренных позже по времени. Один вариант заключается в том, чтобы начинать обработку до некоторой степени вглубь данных и продвигаться назад для получения первоначальной оценки для прогона вперед. Другой вариант заключается в использовании ранее упомянутых модификаций фильтра Рауха, которые включают в себя все данные впереди текущей выборки. Принципу Рауха присущи проблемы с модифицированным уравнением состояния (9) и (10) из-за зависимости матрицы перехода Ф от данных. Выход фильтра Калмана будет представлять собой оптимальные (с минимальной среднеквадратической ошибкой) значения вектора состояния и соответствующие ковариационные матрицы ошибок сигнала (строки с сообщениями об ошибках). В другом алгоритме отслеживания может использоваться другой критерий минимизации ошибок. В заключение описания работы фильтра Калмана в предложенном способе обратимся снова к фиг. 2. На этапе 21 оцениваются первоначальные значения для вектора состояния и его ковариации на некоторой временной выборке. На этапе 22 алгоритм Калмана вычисляет коэффициент Калмана Kk путем оценки показанного уравнения. Коэффициент Калмана Kk определяет, как следует модифицировать измеренные данные для их оптимального объединения с предположением вектора состояния. Это объединение данных выполняют на этапе 23. На этапе 24 оценивается ковариация ошибок для новой оценки. И,наконец, на этапе 25 новая оценка используется для проекции вперед по времени на следующую выборку, и процесс повторяется. При обработке каждой выборки решение для этой выборки определяется методом наименьших квадратов на этот момент времени путем непосредственной оценки уравнений в процессе решения. Уравнения состояния и измерений определяют, как развивается состояние системы и как данные измерений соотносятся с этим состоянием системы. Ковариационные матрицы Qk и Rk на фиг. 2 соответствуют величинам wk и rk в уравнениях состояния и измерений. Значения Qk обычно определяются методом проб и ошибок, они характеризуют, насколько быстро фильтр реагирует на изменения данных. Значения Rk определяются из дисперсии шумов (ожидаемое значение квадрата шума) и ковариации шумов (корреляции между составляющими шума, если это необходимо). Кроме наилучшего решения методом наименьших квадратов для вектора состояния xk алгоритм Калмана также дает соответствующую ковариацию ошибок для этого решения. Конечно, оптимальный характер такого решения зависит от точности определения уравнения состояния и уравнения измерений, включая требуемые ковариационные матрицы для шумов состояния и измерений. Оптимальную оценку вектора состояния можно использовать несколькими способами во время фазы интерпретации (этап 34 на фиг. 3). Например, оценку сигнала xs можно сравнить с параметрическими моделями для выбора из нескольких смоделированных структур удельного сопротивления. Альтернативно xs можно использовать в качестве ввода в инверсию для структуры удельного сопротивления. В любых параметрических исследованиях или инверсии вместо xs можно также использовать А и v. Другим методом интерпретации является использование А и v в "быстрой" одномерной или двумерной инверсии. В одном, таком варианте эти элементы состояния вектора блокируются, чтобы дать кусочно-экспоненциальные функции амплитуды, которые будут соответствовать отдельным слоям в упрощенной геологии. Пример. На фиг. 5-10 проиллюстрирован пример с моделированными данными горизонтального электрического диполя. На фиг. 5 представлены моделированные данные с аддитивным случайным шумом. Частота сигнала составляет 0,25 Гц и затухает приблизительно экспоненциально от нулевого положения времени. Аддитивный шум взят из зарегистрированного магнитнотеллурического шума окружающей среды. На фиг. 6 показан снимок таких зашумленных входных данных (исходный сигнал плюс аддитивный шум) 61 приблизительно на 5000 секундах. На том же графике представлена часть 62 моделированных данных сигнала, свободного от шумов, и оценка 63 сигнала, полученная с помощью предложенного способа. Оценка 63 почти равна свободному от шумов сигналу 62, и их трудно различить на фиг. 6. Такое близкое сходство является мерой успеха настоящего изобретения, поскольку моделированный сигнал не известен для способа. Даны только введенные зашумленные данные, однако изобретение позволяет восстановить часть сигнала. В варианте настоящего изобретении, использованном в данном примере, в качестве алгоритма отслеживания применяется фильтр Калмана, но можно также применять описанный выше предпочтительный алгоритм. Сдвиг, который соответствует представленной на фиг. 6 части, составляет приблизительно 4000 м. На фиг. 7 показана скорость изменения амплитуды свободного от шумов сигнала А (сплошная кривая 71) и вычисленное значение А (рваная кривая 72), полученное фильтром Калмана с использованием зашумленных данных. Можно заметить, что эта оценка имеет наилучшее качество в центральных частях данных, где сигнал имеет самую высокую силу. На фиг. 8 показана скорость изменения относительной фазы v свободного от шумов сигнала(сплошная кривая 81) и вычисленное значение v (рваная кривая 82), полученное фильтром Калмана с использованием зашумленных данных. И здесь также оценка имеет наилучшее качество в центральных частях данных, где сигнал имеет самую высокую силу. На фиг. 9 проиллюстрирована амплитуда сигнала входных данных, свободных от шумов (сплошная кривая 91) по сравнению с оценкой Калмана (штриховая линия 92). Этот полулогарифмический график показывает изменение силы сигнала на более чем три порядка величины. На фиг. 10 показано аналогичное сравнение относительной фазы входного сигнала 101 с оценкой Калмана 102. Представленное выше описание направлено на конкретные варианты настоящего изобретения в целях его иллюстрации. Однако специалистам будет понятно, что в описанные варианты можно внести множество модификаций и изменений. Все такие модификации и изменения подпадают под объем притязаний настоящего изобретения, охарактеризованный в прилагаемой формуле изобретения. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ отслеживания изменений амплитуды и фазы передаваемого периодического электромагнитного сигнала в зашумленных данных, обнаруженных в течение времени по меньшей мере одним приемником, причем данный сигнал передают с известной частотой, заключающийся в том, что:(a) выбирают алгоритм отслеживания для отслеживания сигнала известной частоты,(b) разделяют время обнаружения на интервалы, в течение каждого из которых обнаруженный сигнал и по меньшей мере один связанный с ним параметр предположительно не изменяются,(c) оценивают первоначальные значения для обнаруженного сигнала и по меньшей мере одного связанного с ним параметра и присваивают эти значения первому интервалу времени,(d) оценивают проекцию первоначального сигнала и каждого связанного с ним параметра на один интервал времени вперед,(e) корректируют первоначальные оценки этапа (d), используя упомянутые данные и алгоритм отслеживания, и(f) повторяют этапы (d)-(e) до тех пор, пока не будут обработаны все данные. 2. Способ по п.1, в котором алгоритм отслеживания является алгоритмом Калмана, включающим в себя вектор состояния, определенный уравнением состояния и уравнением измерений, причем вектор состояния имеет по меньшей мере две следующие составляющие - амплитуду обнаруженного сигнала и упомянутый по меньшей мере один выбранный связанный с сигналом параметр. 3. Способ по п.2, в котором вектор состояния имеет две составляющие и упомянутый по меньшей мере один связанный с сигналом параметр пропорционален производной сигнала по времени (квадратурному сигналу). 4. Способ по п.2, в котором вектор состоянии имеет четыре составляющие: амплитуду сигнала, амплитуду квадратурного сигнала, скорость изменения амплитуды огибающей сигнала со временем и скорость изменения относительной фазы сигнала со временем, причем последние две составляющие используются для отслеживания сигнала, испытывающего существенное затухание. 5. Способ по п.2, в котором алгоритм Калмана адаптирован для использования данных, обнаруженных позже по времени, на этапе корректировки. 6. Способ по п.1, в котором дополнительно осуществляют масштабирование первоначальных данных. 7. Способ по п.1, в котором передаваемый сигнал является Фурье-составляющей сигнала источника при электромагнитной разведке подземной формации. 8. Способ по п.7, в котором на последнем этапе определяют структуру удельного сопротивления подземной формации из оценок сигнала или по меньшей мере одного из связанных с ним параметров. 9. Способ по п.2, в котором в уравнении состояния применяют небольшую корректирующую линеаризацию. 10. Способ по п.2, в котором оценку сигнала и связанной с ним ошибки получают для каждого периода времени. 11. Способ по п.4, в котором алгоритм Калмана модифицируют, чтобы позволить ввести А (скорость изменения амплитуды огибающей сигнала по времени) и v (скорость изменения относительной фазы сигнала по времени) в вектор состояния, с использованием предположения для небольшой корректирующей линеаризации, согласно которому предполагается, что (i) амплитуда огибающей сигнала умножена на (1+TА), где А - скорость изменения амплитуды огибающей сигнала по времени и T - интервал времени, и (ii) сигнал подвержен фазовому сдвигу vT, где v - скорость изменения относительной фазы сигнала и vT предположительно 1.