Метод уплотнения данных
Формула / Реферат
1. Способ сжатия массива х из N значений, представляющего характеристики земли, включающий в себя следующие этапы:
(a) разбиение массива х на блоки из М значений, где М < N,
(b) свертывание значений xI(j) = x(IM+j) поперек границы каждого блока I, так что
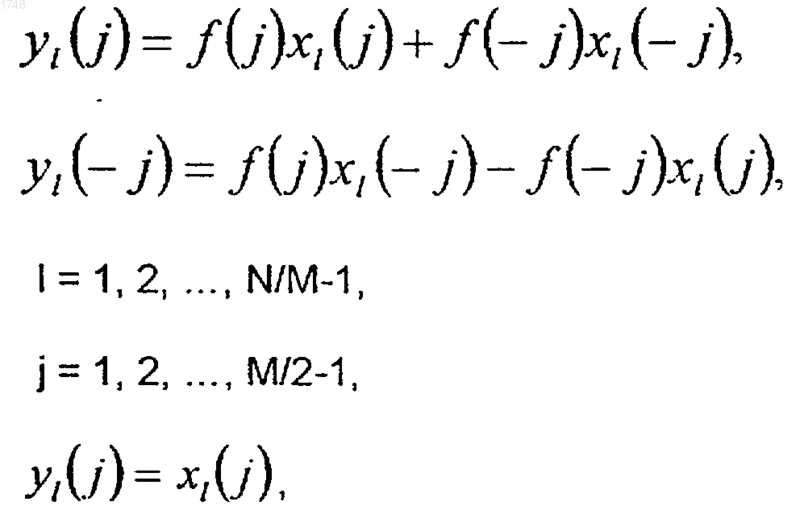
где
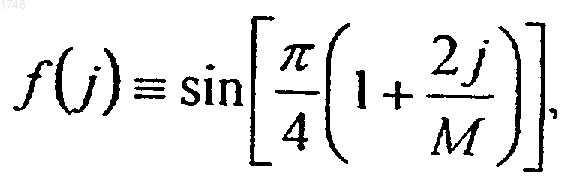
(с) преобразование свернутых значений в каждом блоке массива y, так что
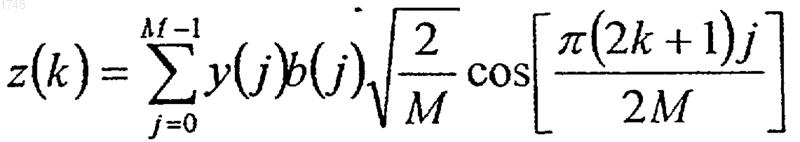
где
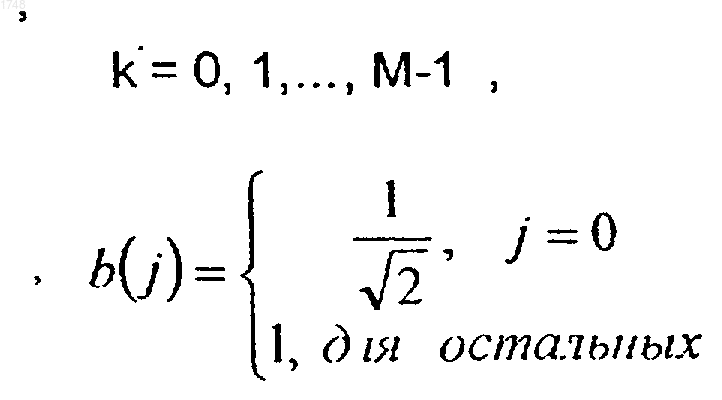
(d) квантование преобразованных значений в каждом блоке массива z для получения целых чисел, и
(e) кодирование целых чисел в поток битов, представляющий собой сжатый массив.
2. Способ по п.1, отличающийся тем, что этапы (а) разбиения на блоки, (b) свертки и (с) преобразования осуществляются последовательно в отношении каждого измерения многомерного массива.
3. Способ по п.2, отличающийся тем, что упомянутые этапы осуществляются в отношении многомерного массива, подмножество которого сжато.
4. Способ по п.3, отличающийся тем, что преобразования осуществляются в отношении многомерного массива, представляющего сейсмические сигналы.
5. Способ по п.1, отличающийся тем, что дополнительно содержит этап распаковки сжатого массива, заключающийся в инвертировании этапов от (а) до (е) в обратном порядке.
6. Способ по п.5, отличающийся тем, что обратные этапы разбиения на блоки (а), свертки (b) и преобразования (с) осуществляются последовательно в отношении каждого измерения многомерного массива.
7. Способ по п.6, отличающийся тем, что упомянутые этапы осуществляются в отношении многомерного массива, подмножество которого подвергнуто распаковке.
8. Способ по п.7, отличающийся тем, что преобразования осуществляют в отношении многомерного массива, представляющего собой сейсмические сигналы.
Текст
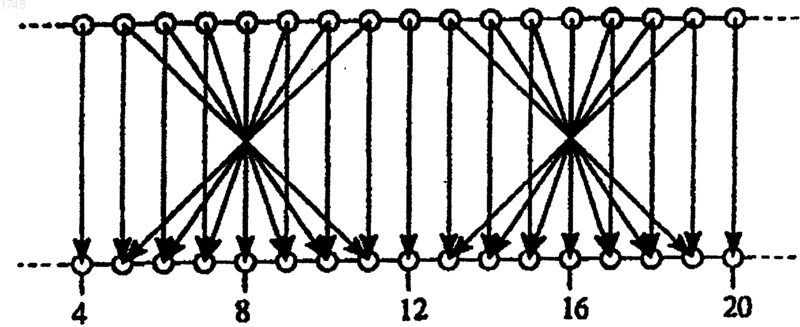
1 Область техники, к которой относится изобретение Эта заявка основывается на предварительной заявке 60/045,915 с приоритетом 7 мая 1997. Область изобретения Изобретение относится в основном к способам сжатия данных и, в частности, к усовершенствованию способа JPEG сжатия изображений, поскольку это изобретение имеет отношение к сейсмическим данным. Описание уровня техники Стандартный способ JPEG сжатия изображений Пеннбакера (Pennebaker) и Митчела(Miteheil) (1993) содержит три этапа, выполняемых для каждого блока пикселей, размером 8 х 8 пикселей в двухмерном массиве: 1. Преобразование блока пикселей, размером 8 х 8 пикселей с использованием дискретного косинусного преобразования (ДКП). 2. Квантование (масштабирование и округление) коэффициентов преобразования в малые целых числа. 3. Кодирование битов с использованием малоразрядного кода, для представления наиболее часто встречающихся целых чисел. При распаковке инвертируют каждый из этих этапов в обратном порядке. Оба способа могут быть легко распространены на сжатие и распаковку массивов данных любого размера. Фиг. 1 изображает двумерный массив сейсмических данных до сжатия. Двумерный массив 32-разрядных чисел с плавающей запятой, изображенный на фиг. 1, соответствует определенному слою в какой-то момент времени,извлеченный из трехмерного массива сейсмических данных. На фиг. 2 показано подмножество того же самого массива в другом масштабе. Фиг. 3 изображает подмножество того же массива в другом масштабе после сжатия и распаковки полного двумерного массива с использованием способа, подобного способу JPEG. Степень сжатия для целого массива составляет приблизительно 103:1, что означает, что первоначальный массив из 32-разрядных чисел с плавающей запятой, содержит приблизительно в 103 раза больше чисел, чем сжатый массив. Для таких больших степеней сжатия применение способа, подобного JPEG вызывает появление искажения изображений блоков, которые можно увидеть на фиг. 3. При более низких степенях сжатия, неоднородности между блоками станут менее заметны, но они будут иметь значение, особенно при дальнейшей обработке, или расшифровке данных после распаковки. Искажения изображения на фиг. 3 - результат сжатия и распаковки каждого блока,размером 8 х 8 пикселей, без попытки сохранить непрерывность между блоками. 2 Несмотря на наличие искажений изображений, очень важна способность к независимому сжатию и распаковке маленьких массивов данных. В частности это позволяет получить доступ к какой-либо части большого сжатого массива, без распаковки всего массива. Это также дает возможность адаптировать способ сжатия к пространственным изменениям данных по амплитуде и спектру. Эти возможности отсутствуют в способах сжатия, основанных на волновых преобразованиях (например, Брэдлей(Bradley) и др., 1993; Викерхаузер (Wickerhauser), 1994). Задача данного изобретения состоит в обеспечении вышеупомянутых возможностей,без появления искажения изображений блоков. Данная проблема может быть решена применением способа сжатия данных, использующем перекрывающиеся блоки, так чтобы распакованные значения могли быть вычислены независимо от смежных значений. Это решение использовалось Йео (Yeo) и Лиу (Liu) (1995), в их адаптации способа JPEG к обработке трехмерных медицинских изображений. Однако использование перекрывающихся блоков увеличивает число блоков, подлежащих сжатию, что увеличивает время вычисления и уменьшает степень сжатия. В данном описании упомянуты в качестве ссылок следующие публикации Брэдлей (Bradley), J. N., С. М. и Хоппер (Hopper), Т., 1993,Волновой/скалярный стандарт квантования ФБИ (FBI) для сжатия полутонового отпечатка пальца. (The FBI wavelet/scalar quantization standard for gray-scale fingerprint image compression):Visual Information Processing II, SPIE Proceedings, 293-304. (ftp://ftp.c3.lan1.gov/pub/WSQ). Джаверт (Jawerth) В. и Свелденс (Sweldens) W., 1995, Биортогональное сглаживание локальных тригонометрических баз: (Biorthogonal smooth local trigonometric bases): J. Fourierpapers/-papers.html). Джаверт (Jawerth) В., Лиу (Liu) Y. и Свелденс (Sweldens) W., 1996, Сжатие сигнала со сглаживанием локальных тригонометрических баз: (Signal compression with smooth local trigonometricD.H., 1989, ЛОТ (LOT) - трансформирующее кодирование без эффектов блокировки (TheProcessing, 37, p. 4, 553-559. Малвар (Malvar) H.S., 1990, Кодирование с перекрытием для эффективного преобразования 3 сжатия данных неподвижных изображений:Nostrand Reinhold. Принсен (Princen) J.P. и Брэдлей (Bradley) А.В., 1956, Проект набора фильтров анализа / синтеза, основанный на временной замене имен домена: (Analysis/synthesis filter bank designTransaction on Acoustics, Speech, and Signal Processing, 34, p. 5, 1153-1161. Викерхаузер (Wickerhauser) M.V., 1994,Адаптивный волновой анализ: от теории до программного обеспечения: (Adapted wavelet analysis from theory to software): A. K. Peters. Йео (Yeo) В. и Лиу (Liu) В., 1995, Передача объемов сжатых трехмерных скалярных данных на основе ДКП: (Volume rendering of DCTbased compressed 3D scalar data: IEEE Transactions on Visualization and Computer Graphics, 1, p. 1, 29-43. В основу изобретения положена задача создать улучшенный способ сжатия JPEG данных, который можно использовать для сжатия небольших подмножеств данных без появления искажений изображений блоков. Краткое изложение сущности изобретения Изобретение предназначено для сжатия данных, в котором используются этапы способа(ДКП) и кодирования Хаффмана (Huffman) для квантования коэффициентов преобразования. Предлагаемый способ является усовершенствованным способом JPEG, заключающийся прежде всего в дополнительных этапах, которые позволяют избежать искажений изображений блоков, и в квантовании коэффициентов преобразования. Краткое описание чертежей Фиг. 1 изображает срез трехмерного массива сейсмических данных в определенный момент времени, который является двумерным массивом 32-разрядных чисел с плавающей запятой, который не подвергался сжатию; фиг. 2 - подмножество двумерного массива, изображенного на фиг. 1, в другом масштабе; фиг. 3 - данные изображенные на фиг. 2 после сжатия и распаковки с использованием способа JPEG, на ней показаны искажения изображений блоков и неоднородности между блоками, размером 8 х 8 пикселей, которые независимо подвергались сжатию; фиг. 4 - данные, изображенные на фиг. 2 после сжатия и распаковки с использованием способа подобного способу JPEG, который был разработан для подавления искажения изображений блоков; фиг. 5 - матрицу СIII-1, соответствующую обратному блочному ДКП-III длины 32, где черные пиксели соответствуют положительным значениям, а белые - соответствуют отрицательным значениям; 4 фиг. 6 - матрицу, соответствующую обратному блочному ДКП-III, с длиной блока равной 8; на фиг. 7 - столбцы 11 и 19 матрицы обратного блочного ДКП-III, изображенной на фиг. 6, где искажения изображения блоков вызваны неоднородностями между блоками при использовании способа сжатия JPEG. Они показаны между выборками 15 и 16, первая выборка в каждой косинусоиде лежит вне кривой, представленной на графике, вследствие неоднородности функции b(j), определяемой уравнением(1 с), что приведено ниже; фиг. 8 - плавно сужающуюся в обе стороны косинусоиду, полученную путем развертки усеченной косинусоиды, изображенной на фиг. 7, которая является столбцами 11 и 19 матрицы обратного свернутого ДКП-III, показанной на фиг. 9; фиг. 9 - матрицу, соответствующую обратному свернутому ДКП-III, в которой столбцы перекрываются от блока к блоку со значениями,которые плавно снижаются до нуля, так чтобы взвешенная сумма эти столбцов не вызывает появления искажений изображений блоков; на фиг. 10 - матрицу, соответствующую операции, используемой для развертки обратного блочного ДКП-III, причем матрица на фиг. 9 получена из той же матрицы, что и изображенная на фиг. 6; фиг. 11 - операцию развертки, которая является парным комбинированием и заменой значений поперек границ блоков матрицы ДКП,при этом свертывание является инверсией этой операции; фиг. 12 - последовательность действий при распаковке выделенной выборки в блоке А, при которой требуется, чтобы данные сначала декодировались, деквантовались и выполнялось обратное ДКП-III блоков А, В, С и D, и затем выполнялась развертка четырех выделенных выборок, где операции свертывания и развертывания являются попарным смешиванием выборок поперек границ блока ДКП. Описание предпочтительного варианта осуществления изобретения Это изобретение предназначено для улучшения способа сжатия данных, основанного на смешивании данных в смежных блоках во время сжатия по способу, подобному способу JPEG. Сжатие данных по способу JPEG было описано многими авторами (например, Princen и Bradley,1986; Malvar и Staelin, 1989; Malvar, 1990; Wickerhauser, 1994, Jawerth и др., 1995). Преимущество такого сжатия данных состоит в том, что оно имеет тенденцию к увеличению степени сжатия, при небольшом увеличении времени вычисления. На фиг. 4 представлено то же подмножество двумерного массива, изображенного на фиг. 1, после сжатия и распаковки с использованием второго способа, подобного JPEG, основанного 5 на данном изобретении, описанном ниже. В этом случае, хотя степень сжатия для полного массива приблизительно равна 112:1, после распаковки отсутствуют искажения изображений блоков. Различие между предшествующими способами, подобными JPEG, и способом согласно изобретению состоит в модификации блочного дискретного косинусного преобразования,имеющего место в стандартном способе JPEG. Эта модификация, содержащаяся в данном изобретении, уменьшает искажения изображений блоков, при сохранении качеств базового способа JPEG. Дискретное косинусное преобразование(ДКП) В предыдущем способе сжатия JPEG использовалось дискретное косинусное преобразование - ДКП-II. В изобретении используется другое дискретное косинусное преобразование ДКП-III. (Нумерацию дискретных косинусных преобразований см. Wickerhauser, 1994, с. 84). ДКП-III. Прямое ДКП-III определяется как и соответствующее ему обратное преобразование Прямые и обратные преобразования могут быть представлены как умножение матриц, причем z = СIIIу и у = СIII-1, где матрица СIII содержит элементы Матрица обратного преобразования CIII-1 изображена при М = 32 на фиг. 5. Любой вектор из 32 вещественных чисел может быть представлен как взвешенная сумма столбцов этой матрицы. В одномерном способе сжатия, вектор у значений может быть аппроксимирован лишь несколькими столбцами матрицы СIII-1. Весовой коэффициент каждого столбца задает коэффициенты преобразования вектора z. Высокие степени сжатия требуют, чтобы многие коэффициенты вектора z были бы малы, стремились к нулю. Такие малые значения коэффициентов будут квантоваться к нулевым значениям, которые далее могут быть эффективно закодированы с использованием небольшого числа битов. В способе JPEG осуществляется сжатие двумерных изображений, а не одномерных векторов. Предыдущее ДКП-II, используемое в способе сжатия JPEG - двумерное преобразова 001748 6 ние. Однако из-за того, что дискретное косинусное преобразование многомерных данных может быть представлено как последовательность одномерных преобразований по каждому измерению, для простоты изложения описывается только одномерное преобразование. Блочное ДКП-III. Для длинных векторов данных, таких как сейсмические трассы, применение дискретного косинусного преобразования целого вектора не позволит определить достаточное количество коэффициентов преобразования. Поэтому как и в способе JPEG используется блочное ДКП с длиной преобразования М = 8, а недостающие данные векторов приравниваются к нулю; если необходимо, чтобы длина N была кратной 8. Матрица, соответствующая обратному блочному ДКП-III, представлена на фиг. 6, для N = 32 и М = 8. Кроме того, для сжатия лучше подходит блочное преобразование, которое эффективно также и сточки зрения стоимости вычислений,которая увеличивается линейно в зависимости от длины N вектора данных. Подобно предыдущему ДКП-II, используемому в способе сжатия JPEG, ДКП-III имеет несколько полезных свойств. Во-первых, ДКПIII преобразовывает вещественные числа в вещественные, поэтому не требуется никаких вычислений с комплексными числами. Так же, как и предыдущее ДКП-II, ДКП-III обеспечивает однозначное преобразованием СIII-1 = СIII1. [Это свойство следует из уравнения (1), приведенного выше]. Матрица прямого блочного ДКП-III,представленная на фиг. 6, просто вычисляется из обратного блочного ДКП-III. Другим полезным свойством является то,что обратное ДКП-III - эквивалентна прямому ДКП-II: СIII-1 = СII. Эта связь между ДКП-III и ДКП-II, и выбор длины преобразования М = 8 позволяет использовать весьма оптимальные для ДКП-II способы, используемые в способе сжатия JPEG простой заменой прямых и обратных этапов. Все свойства, указанные выше полезны, но почему не так просто использовать предыдущее ДКП-II Ответ находится в модификации ДКПIII согласно изобретению, чтобы избежать искажений изображений блоков, вызванных сжатием JPEG. Искажения изображений блоков появляются только тогда, когда для аппроксимации вектора используется только подмножество столбцов матрицы, показанных на фиг. 6. Предположим, что такой вектор сильно сжат с использованием только двух столбцов c k=11 иk=19. Как это следует из фиг. 7, любая нетривиальная комбинация из этих двух столбцов в приближении имеет неоднородность между данными с индексами j = 15 и j =16. Такие неоднородности создают искажения изображений блоков, видимые на изображениях, которые были сжаты с использованием способа JPEG. 7 Свернутый ДКП-III. Чтобы избежать появления искажений изображения, вызванных использованием блочного ДКП-III, в сжатии косинусоида в блоках,представленная на фиг. 7, заменяется плавносужающейся в обе стороны косинусоидой, изображенной на фиг. 8. При сравнении законченной матрицы обратного преобразования, изображенной на фиг. 9 с матрицей обратного блочного ДКП-III на фиг. 6, видно, что число выборок в каждом косинусе увеличено до 16(кроме концов), так чтобы косинусоиды в смежных блоках перекрывались, и так чтобы каждая косинусоида плавно приближалась к нулю. Взвешенная сумма этих косинусоид не вызовет неоднородностей, показанных на фиг. 7. Преобразования, основанные на таких плавносужающихся косинусоидах, часто называют локальными косинусными преобразованиями, или ортогональными преобразованиями(Wickerhauser, 1994, с. 370; здесь имеется сходство между фиг. 8 и 11.5 в Wickerhauser). Здесь эти преобразования упомянуты как свернутые косинусные преобразования, и они отражают способ, которым они были произведены. Так преобразование, используемое в способе сжатия, согласно изобретению - есть свернутое ДКП-III. Обратное преобразование, соответствующее матрице, изображенной на фиг. 9, названо обратным свернутым ДКП-III. Свертка - способ достичь плавного сужения 16-значений косинусов с использованием высокооптимизированного блочного М = 8 ДКП. Wickerhauser (1994, с. 103) описывает этот способ и описывает его применение к процессу сжатия. Операция свертки, используемая при сжатии в данном изобретении, - одна из многих,описанных Wickerhauser, но получила право на жизнь работами Jawerth и Sweldens (1995) иJawerth и др. (1996). Позже аспекты свертки обсуждались другими авторами, как являющиеся приемлемыми для сжатия. Разумность и эффективность свертки заключается в том, что матрица обратного свернутого ДКП-III, изображенная на фиг. 9, является результатом развертки матрицы, показанной на фиг. 10, и матрицы обратного блочного ДКП-III,показанной на фиг. 6. Поскольку каждая строка и столбец развернутой матрицы содержат не больше, чем два ненулевых элемента, стоимость вычисления развертывания является незначительной по сравнению со стоимостью вычислений обратного блочного ДКП-III. На практике, матрицы, изображенные на фиг. 6, 9 или 10, фактически никогда не получают. Более того, операции, выполненные на выборочных значениях, имеют тот же самый эффект, что и умножение этих матриц. Для матрицы обратного блочного ДКП-III, показанной на фиг. 6, эта операция является высокоэффективным прямым блочным ДКП-II, при исполь 001748 8 зовании ее в способе сжатия JPEG. Для развернутой матрицы на фиг. 10 эта операция представляет собой парное смешивание значений поперек границ блоков при индексах j = 8, 16, , как это проиллюстрировано на фиг. 11. Операция свертки является инверсией операции развертки, т.е. различное парное смешивание тех же самых значений. Поскольку свертывание и развертывание центрированы относительно границ блоков, эти операции можно кратко определить в виде сдвинутых значений,которые определяются как у 1(j) = y(IM + j). Где символ I является индексом блока и j - индексом значения внутри блока. Тогда, свертывание производится следующим образом: и операцию развертывания производится следующим образом: где функция свертки f(j) определяется посредством Плавносужающийся косинус на фиг. 8 и матрица таких косинусов на фиг. 9 были вычислены из столбцов матрицы, изображенной на фиг. 6, с использованием уравнений (3b). Прямое свернутое ДКП-III значений x(j) определяется вычислением y(j) по уравнению(3 а), затем для каждого блока из 8 выборок вычисляется z(k) по уравнению (1a). Аналогично,обратное свернутое ДКП-III определяется вычислением y(j) по уравнению (1b) для каждого блока, а затем вычислением x(j) по уравнению(3b). Как показано в Wickerhauser (1994, с. 105),Jawerth и Sweldens (1995) и Jawerth и др. (1996),существует много альтернативных, но похожих способов свертки. Операция свертки, определяемая уравнением (3), выбрана по двум причинам. Во-первых, операция свертки однозначна. Развернутая матрица, показанная на фиг. 10,получается транспонированием соответствующей свернутой матрицы (она не показана). Чтобы убедиться в этом, достаточно увидеть, что функция свертывания по уравнению (3 с) удовлетворяет условию f2(j)+f2(-j)=1, и затем выразить операции свертки и развертки в соответствии с уравнениями (3 а) и (3b) как умножение 9 матриц размером 2 х 2. Аналитически инверсия свернутой матрицы размером 2 х 2, как можно видеть, соответствует ее транспонированной матрице, равной развернутой матрице, размером 2 х 2. В целом, операция свертки поэтому и однозначна, потому что она состоит из смешивания 2 х 2 значений поперек границ блоков. Во-вторых, операция свертки в соответствии с изобретением гарантирует, что постоянная функция, такая как x(j) = 1, даст коэффициенты преобразования zI(k) в каждом блоке, и ненулевыми они будут только для k = 0, поэтому и увеличивается степень сжатия констант (или медленно меняющихся данных). В терминологии, предложенной Jawerth и др. (1996), прямое свернутое ДКП-III достигает "разрешающей способности константы". Чтобы убедиться в этом втором свойстве свернутого ДКП-III, применим аналитическую операцию свертывания по уравнениям (3 а) к постоянном значениям XI(j) = 1, и проверим, что в результате где CIII(k,j) определены уравнением (2). Другими словами, функция свертки выбрана так, чтобы постоянные значения сворачивались так,чтобы точно соответствовать (с точностью до масштабного коэффициента М) первому (k = 0) косинусу ДКП-III. Поскольку этот косинус ортогонален ко всем другим косинусам этого преобразования, коэффициенты преобразования в каждом блоке будут отличны от нуля при k = 0 только после применения прямого свернутого ДКП-III. Значение каждого ненулевого коэффициента будет zl(0) = M. Более точно, это справедливо для всех,кроме первых и последних, блоков. Хотя разрешающая способность констант для первых и последних блоков может быть получена путем модификации матриц свертки и развертки, так чтобы они не были однозначными в углах, для этих блоков принята меньшая степень сжатия и поэтому сохраняется свойство того, что операции свертки и развертки однозначны. Сравнение с ДКП-II, используемом в способе сжатия JPEG Вначале ДКП-II использовалось в способе сжатия JPEG для достижения разрешающей способности констант без свертывания, потому что первый косинус ДКП-II (например, первая строка матрицы на фиг. 5) постоянен. В действительности, это свойство и есть причина того,почему ДКП-II, а не ДКП-III, определяет сжатие в способе JPEG. Можно предположить использование свертки в ДКП-II, потому что свертку перед JPEG сжатием и развертку после JPEG сжатия можно выполнить без какого-либо изменения в стандартном способе сжатия JPEG. К сожалению, операции свертки и развертки в соответствии с уравнениями (3) не соответствуют ДКП-II. Действительно, по уравнениям(3b) не получится плавносужающийся косинус,подобно изображенному на фиг. 8.Jawerth и др. (1995) описывают альтернативные операции свертки и развертки, которые соответствуют ДКП-II, и это обеспечивает разрешающую способность констант. Однако эти операции не однозначны. Они фактически некорректны, имеют тенденцию усиливать неоднородности в значениях, которые появляются около границ блоков, и таким образом уменьшают эффективность сжатия. В противоположность этому, операции свертки и развертки на основе уравнений (3) однозначны, так же как и прямое и обратное ДКП-III согласно уравнениям (1). Если через F обозначить свернутую матрицу, то тогда прямое свернутое ДКП-III может быть выражено как z = СIIIFx, и видно, что Другими словами, сумма квадратов значений после свернутого ДКП-III равняется той же сумме перед свернутым ДКП-III. Это свойство может быть использовано для оценки искажений данных после распаковки, вызванных квантованием коэффициентов преобразования. Квантование и кодирование Как описано выше, преобразование, использованное в способе сжатия по данному изобретению, является инверсией преобразования,используемого в способе сжатия JPEG, но со сверткой для уменьшения искажения изображений блоков. Используемые этапы квантования и кодирования также адаптированы применительно к используемым в способе сжатия JPEG. Различия между способом JPEG и по данному изобретению описаны ниже. Квантование Поскольку способ сжатия JPEG предназначен для изображений, то данные перед сжатием представлены 8- или 12-разрядными значениями (цветные изображения представлены красно-зелено-синими триплетами таких выборок). После двумерного преобразования с помощью ДКП-II, 8-разрядным данным может потребоваться до 11 разрядов, потому что самое большое значение после двумерного ДКП-II может увеличиться до 8 раз по отношению к тому, что было перед преобразованием. Обычно, самое большое значение после ДКП-11 может увеличиться до МD/2 раз по отношению к значению перед преобразованием, где D - размерность преобразования. Другими словами Этот верхняя граница достигается тогда,когда данные точно соответствуют одному из 11 косинусов, используемых в ДКП-II, такого как постоянного первого косинуса CII(k=0, j). Тот же самый коэффициент МD/2 также используется применительно к свернутому ДКПIII, используемому в способе сжатия по этому изобретению. Поэтому после преобразования целочисленных 8-разрядных данных с помощью свернутого ДКП-III, в соответствии с методом квантования и кодирования по данному изобретению подвергают 11-разрядные целые числа двумерному сжатию, а целые 13-разрядные числа - трехмерному сжатию. Этап квантования, как и в способе сжатияJPEG, так и в изобретении является масштабированием, таким чтобы уменьшить число разрядов, которые будут закодированы, и именно это сокращение числа разрядов отвечает за искажение данных, которые сначала подвергаются сжатию, а затем подвергают распаковке. В таких способах сжатия с потерями эти искажения допускается в обмен на высокие степени сжатия. В способе сжатия JPEG, коэффициенты преобразования внутри каждого блока квантуются по-разному, с высокими волновыми числами (пространственными частотами), представляемыми меньшим количеством разрядов,чем низкие волновые числа. Это масштабирование, зависимое от волновых чисел при JPEG сжатии, обычно оптимизируется в соответствии со зрительным восприятием человека. В способе сжатия по данному изобретению, все волновые числа квантуются одинаково. Ошибки не представлены, поскольку они зависят от волнового числа. Одна причина этого в том, что для сейсмических данных часто представляют интерес высокие волновые числа. Например, дефекты подложки изображения с сейсмическими данными соответствуют высоким волновым числам. Другая причина в том,что сейсмические данные часто анализируются с помощью компьютеров, которые не учитывают особенности человеческого зрения. Локальное квантование При сжатии 8-разрядных данных изображения, значения данных лежат между -128 и+127 и можно принять, что блоки данных с низкой амплитудой являются незначащими и могут быть безопасно округлены до нуля во время сжатия. В способе JPEG, в частности, это допускается, поскольку это позволяет получить один набор масштабных коэффициентов квантования для всего изображения. Как обсуждалось выше, эти масштабные коэффициенты могут варьироваться (различные волновые числа) в пределах блока, но для каждого блока используется один и тот же набор волновых чисел. В этом смысле, квантование, используемое в способе JPEG - глобально. При сжатии 32-разрядных данных с плавающей запятой, предпочтительно выполнять локальное квантование с масштабными коэф 001748 12 фициентами, которые изменяются от блока к блоку. Поэтому перед сжатием таких данных их максимальное значение амплитуды xmax не известно, и проверка каждого значения перед сжатием для его определения может быть весьма дорогостоящей. Кроме того, малые значения не могут быть приняты как незначащие, поскольку сейсмические данные часто требуют большой обработки прежде, чем это предположение могло быть принято. Поэтому хотя и используется единый масштабный коэффициент для квантования всех коэффициентов преобразования в пределах блока, его можно разрешить изменять от блока к блоку. Таким образом, в приведенном выше уравнении (5) zmax обозначает максимальный коэффициент в пределах каждого преобразуемого блока, и различные масштабные коэффициенты, вычисляемые для каждого блока. Локальное квантование обеспечивает более низкие степени сжатия (производит больше"битов в выборке"), чем глобальное квантование. Очевидная причина этого в том, что требуются дополнительные биты, для сохранения масштабных коэффициентов квантования для каждого блока, подлежащего сжатию. Менее очевидная причина в том, что локальное квантование может при квантовании дать меньшее количество нулей, чем глобальное квантование. Поэтому и производится выбор либо локального, либо глобального квантования в способе сжатия по данному изобретению. Локальное квантование не может иметь дело с большим динамическим диапазоном в пределах одного блока. Например, низко амплитудные отражения в необработанных сейсмических данных могут быть скрыты в высоко амплитудных поверхностных волнах. Внутри блоков, на которые наложен высоко амплитудный шум, способ сжатия по данному изобретению даже с локальным квантованием может квантовать низко амплитудный сигнал в нуль, так что сигнал не может быть восстановлен после распаковки. Поэтому высоко амплитудный шум должен быть уменьшен перед сжатием. Сжатие в виртуальной памяти Виртуальная память представляет собой память большую, чем это существует физически. Виртуальная память наиболее эффективна для тех приложений, которые обращаются к данным, расположенным около данных, к которым недавно обращались. Такие приложения имеют хорошую локализацию ссылок. Приложения, работающие с двумерными или трехмерными массивами, имеют хорошую локализацию ссылок. Например, приложение обработки сейсмических данных может отображать последовательные двумерные слои данных из трехмерного массива. С помощью способа локальной распаковки достаточно быстро, могут быть распакованы блоки, содержащие выборки из тех слоев, какие требуются, без распаковки 13 всего трехмерного массива. Способ сжатия по данному изобретению особенно полезен для таких приложений. Ключом к таким приложениям является способность к сжатию и распаковке подмножеств большого массива, без сжатия или распаковки всего массива. Это свойство легко достичь для сжатия, основанного на блочном ДКПII, подобно тому, что используется в JPEG сжатии. Так, чтобы распаковать одну выборку, необходимо провести декодирование, деквантование и обратное ДКП-II блока, содержащего эту выборку. Как только распаковка для одной этой выборки выполнена, распаковка всех остальных выборок того же блока также является выполненной. Принимая такую локализацию ссылок,стоимость вычисления распаковки других выборок в этом блоке не будет очень большой. Для способа сжатия, предложенного в данном изобретении, основанного на свернутом ДКП-III, требуется некоторая дополнительная работа. Рассмотрим двумерное сжатие и четыре блока размером 8 х 8 значений, изображенных на фиг. 12. Чтобы распаковать выборку, соответствующую заполненному кругу в блоке А, требуется(1) декодировать, деквантовать и выполнить обратное ДКП-III всех четырех блоков (А,В, С и D);(2) развернуть четыре выборки, соответствующие заполненным кругам. Развертка поперек границ блоков проводится так, как это изображено на фиг. 11 и описано уравнением (3b),т.е. сначала выполняется для одного измерения,а затем для других. Хотя для данной операции требуются четыре блока, но как только распаковка выборки в блоке А выполнена, большинство работы, необходимой для распаковки соседних выборок, также уже выполнено. Снова,принимая во внимание локализацию ссылки, это дополнительное вычисление не будет очень большим. Другое отличие между этапами квантования данного изобретения и основного способа сжатия JPEG, состоит в необходимости квантования 32-разрядных данных с плавающей запятой, которые имеют гораздо больший диапазон,чем измененные 8- или 12-разрядные данные изображения. Для квантования значения с плавающей запятой z в целое число i с использованием В+1 разряд (включая знаковый разряд),производят следующие действия где s - коэффициент масштабного квантования. Для того чтобы не возникло переполнение, требуется, чтобы i2B. Это ограничение и уравнение (6) ведут к следующему уравнению для вычисления коэффициента масштабирования: где- наименьшее положительное число, которое можно вычесть из 1 с использованием арифметики с плавающей запятой, для того чтобы получить число, не равное 1. Кодирование Хаффмана В стандартном способе сжатия JPEG имеется два способа кодирования целых чисел, полученных квантованием, кодирование Хаффмана и арифметическое кодирование, также возможно много других методов кодирования. В способе JPEG используется кодирование Хаффмана, которое также используется и в способе сжатия по данному изобретению, потому что оно быстро вычисляется, просто в осуществлении и доступно. С одним исключением алгоритмы кодирования и декодирования Хаффмана удовлетворяют требованиям способа JPEG. В способеDC коэффициенты часто бывают сильно коррелированы с соседними блоками. Это не используется в способе по данному изобретению, по двум причинам(1) это представляет собой зависимость"блок-от-блока" которая усложняет сжатие и распаковку отдельных блоков;(2) сейсмические данные обычно имеют сравнительно малые DC коэффициенты. (Хотя и малые, DC коэффициенты редко не принимаются в расчет из-за короткого преобразования при М=8). Поэтому DC коэффициенты кодируются так же, как и другие (АС) коэффициенты. Локальная компрессия Главное преимущество способа, подобного способу JPEG состоит в том, что часть многомерного массива может быть сжата или использована без обработки всего массива. Напротив, в способах сжатия, основанных на волновых преобразованиях (например, Bradley и др. 1993;Wickerhauser, 1994) этого нет. Но, несмотря на то, что в способе JPEG это явно не выражено,блочное ДКП-II, используемое в способе сжатияJPEG, дает такую возможность. Эта возможность используется в способе сжатия по данному изобретению, основанного на свернутом ДКП-III. Каждый блок данных в массиве можно представить, по аналогии, как страницу виртуальной памяти. Для двумерного сжатия каждая такая страница содержала бы 64=8 х 8 выборок; для трехмерной - 512=8 х 8 х 8 выборок. Выборки распакованы, когда они открыты, а волновое числа сжаты, когда они считаны из волновых чисел. Рабочее количество несжатых страниц хранится в памяти, в то время как большинство страниц остается в сжатом состоянии и хранится или в памяти или на диске. (Если они сохранены на диске, то страницы могут быть объеди 15 нены, чтобы повысить эффективность вводавывода). Если рабочее количество достаточно большое и если в нашем приложении хорошая локализация ссылки, то стоимость вычислений сжатия и/или распаковки каждой страницы будет поглощена доступом к большинству выборок внутри той же страницы. Адаптация способа сжатия JPEG, согласно изобретению, позволяет использовать многие этапы этого же способа. Способы JPEG используются для 8-разрядного ДКП путем замены прямых и обратных преобразований. Способ квантования JPEG был изменен, чтобы избежать обработки данных с низкими волновыми числами, и для обработки изменений в амплитудах данных "от блока к блоку". Значения также сворачиваются поперек границ блоков перед прямым ДКП, и разворачиваются после обратного ДКП. Операции свертки и развертки подавляют искажения изображений блоков, видимые в изображениях, сжатых с помощью способа JPEG. Для сравнения способов по данному изобретению с другими способами существует два критерия эффективности - время вычислений и искажения при определенной степени сжатия. Проведенные эталонные тесты с более ранней версией способа по этому изобретению дают положительный результат. Время вычисления уменьшилось и примерно наполовину, а искажения остались практически на том же уровне для широкого диапазона степеней сжатия (Diller, 1997). Время вычислений, предположительно, меньше для способа по данному изобретению по сравнению с волновыми способами (изза меньшего количества операций сложения и умножения и более рационального использования памяти). ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ сжатия массива х из N значений,представляющего характеристики земли, включающий в себя следующие этапы:(a) разбиение массива х на блоки из М значений, где МN,(b) свертывание значений xI(j) = x(IM+j) поперек границы каждого блока I, так что(с) преобразование свернутых значений в каждом блоке массива y, так что где(d) квантование преобразованных значений в каждом блоке массива z для получения целых чисел, и(e) кодирование целых чисел в поток битов, представляющий собой сжатый массив. 2. Способ по п.1, отличающийся тем, что этапы (а) разбиения на блоки, (b) свертки и (с) преобразования осуществляются последовательно в отношении каждого измерения многомерного массива. 3. Способ по п.2, отличающийся тем, что упомянутые этапы осуществляются в отношении многомерного массива, подмножество которого сжато. 4. Способ по п.3, отличающийся тем, что преобразования осуществляются в отношении многомерного массива, представляющего сейсмические сигналы. 5. Способ по п.1, отличающийся тем, что дополнительно содержит этап распаковки сжатого массива, заключающийся в инвертировании этапов от (а) до (е) в обратном порядке. 6. Способ по п.5, отличающийся тем, что обратные этапы разбиения на блоки (а), свертки(b) и преобразования (с) осуществляются последовательно в отношении каждого измерения многомерного массива. 7. Способ по п.6, отличающийся тем, что упомянутые этапы осуществляются в отношении многомерного массива, подмножество которого подвергнуто распаковке. 8. Способ по п.7, отличающийся тем, что преобразования осуществляют в отношении многомерного массива, представляющего собой сейсмические сигналы.
МПК / Метки
МПК: G06K 9/36
Метки: уплотнения, данных, метод
Код ссылки
<a href="https://eas.patents.su/11-1748-metod-uplotneniya-dannyh.html" rel="bookmark" title="База патентов Евразийского Союза">Метод уплотнения данных</a>
Предыдущий патент: Гидрофонный модуль для морского сейсмического кабеля
Следующий патент: Способ и устройство для электрохимической обработки
Случайный патент: Гибридный белок проинсулина и способ получения из него рекомбинантного инсулина












