Модельный элементарный флексор

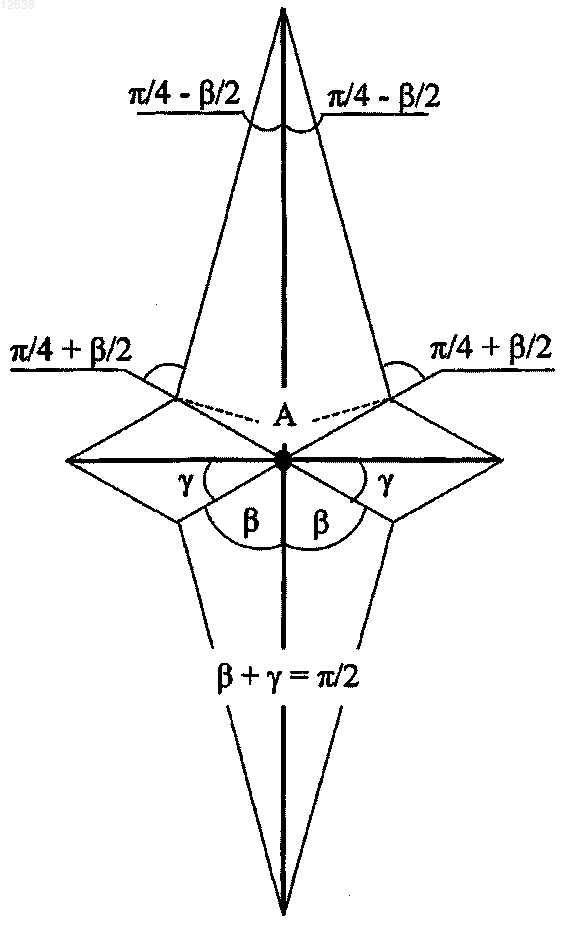
012538 Настоящее изобретение принадлежит к различным областям техники и промышленности, где применяются полиэдральные оболочки, в первую очередь к строительству, к авиационной и корабельной промышленности и к точному приборостроению. Может быть использовано для разработки конструкций со сменной геометрической формой. В частности, рассматриваются тонкие упругие полиэдральные оболочки постоянной толщины. Срединные поверхности у этих оболочек - полиэдры. В различных применениях, в теоретических и технических расчетах, оболочки задаются своими срединными поверхностями. Полиэдральные оболочки применяются в основном в строительстве [1, 2]. Они используются и в других технических областях при проектировании конструкций по конечно-элементному методу. Растущее значение полиэдральных оболочек подчеркивается известным примером из военной авиации: американский самолет F-117A имеет фюзеляж пирамидальной конфигурации, которая является одним из его существенных технологических достоинств [3]. Главное требование к любой оболочке, в частности к полиэдральной оболочке, - устойчивость в эксплуатации. Предмет настоящего изобретения выходит на другие конструкции. Мы имеем дело с полиэдральными оболочками, которые допускают при маленьких нагрузках значительные контролируемые изменения геометрической формы. В технической практике подобные подвижные конструкции неизвестны. Как исключительный пример, здесь можно привести знакомые лишь геометрам материальные модели нежестких сфероидных простых полиэдров-флексоров и жестких открытых правильных звездчатых пирамид. Простыми называются полиэдры, если они не имеют самопересечений. Нежесткими называются полиэдры, которые допускают непрерывные изгибания по О. Коши. Т.е. деформации, при которых грани перемещаются как твердые пластины, так что длины кромок постоянны и изменяются лишь двугранные углы между соседними гранями. Напомним, что в общем понимании изгибание - это изометрическая деформация поверхности. Понятие флексор было введено Р. Коннелли, который впервые доказал существование простых, допускающих изгибание полиэдров-сфероидов. Материальная модель такого флексора, которая представляет собой оболочку постоянной толщины, носит название теоретического флексора. В технической литературе термину теоретический флексор отвечают разные наименования: механизм и кинематический механизм (рус.), механизм в себе (фр.), точный механизм(англ.). В практике термин механизм часто относят к феномену разрушения конструкции. С другой стороны, существование самого механизма не обсуждается, поскольку оболочки используются лишь в том случае, если их стабильность спрогнозирована обычными экспериментальными методами. На данное время известно всего три полиэдра-флексора коннелливского типа. Они были обнаружены в 1978 г., авторы - Р. Коннелли (18 вершин), Н. Кейпер и П. Делинь (11 вершин), К. Стефен (9 вершин) [4]. По опыту известно, что полиэдральные оболочки, построенные на базе этих флексоров, т.е. теоретические флексоры, допускают большие свободные, без видимых искажений материала деформации в классе полиэдров; здесь деформации свободные, если они приводят к достаточно малым нагрузкам. Такие трансформации полиэдральных оболочек являются однозначными и обратимыми, довольно точно воспроизводящими некоторые изгибания срединной поверхности оболочки. Конкретно упомянутые качества деформаций имеют следующие конкретные последствия. При незначительной нагрузке оболочка непрерывно деформируется с амплитудой деформации, сравнимой с габаритными размерами. Грани оболочки, вращаясь вокруг ребер, перемещаются практически как твердые пластины. Напряжения в оболочке, которые возникают от приложенных усилий, разгружаются в маленьких окрестностях ребер,реально стабилизируя всю систему ребер оболочки. В данном случае оболочку, которая обладает перечисленными качествами, будем называть геометрически изгибаемой в классе полиэдров. Это определение относится как к замкнутым, так и к открытым оболочкам, или панелям. Более того, оно может относиться к оболочкам с жесткими срединными поверхностями, что является принципиально важным. Геометрическая изгибаемость теоретических флексоров известна по опыту, это вызвано нежесткостью срединного полиэдра оболочки. Некоторые оболочки с жесткими срединными поверхностями, которые являются геометрически изгибаемыми подобно теоретическим флексорам, открыты автором недавно [5, 6, 7], с помощью отдельных полиэдров, правильных звездчатых пирамид. Естественно называть такие полиэдры модельными флексорами. На основании названных работ автором был получен патент Украины 54692. Термин идеальный подчеркивает вид потери устойчивости оболочкой, который был предусмотрен еще Л. Эйлером, рассматривался в литературе как потеря устойчивости в малом [8]. Это устройство не имеет аналогов, так как достигаемый им технический результат основывается на новом и неожиданном феномене в теории оболочек, который был открыт автором. В частности, было открыто, что оболочка с жесткой срединной поверхностью должна допускать нежесткую - мягкую или затянутую - потерю устойчивости. Это неожиданно, так как в механике еще до настоящего времени придерживаются следующего принципа жесткости: оболочка с жесткой срединной поверхностью будет устойчивой в эксплуатации [1, 2]. Описанный модельный идеальный флексор будет принят в качестве прототипа для нового устройства, заявляемого здесь, поэтому будет полезно привести его формулу. Модельный идеальный флексор представлен правильной звездчатой пирамидой или построенной на базе пирамиды с сохранением в плане ее вариантов симметрии и выпуклости лепестков звездчатой шатровой полиэдральной панели из тонких упругих граней с шарнирными соединениями. Панель имеет плоский край, к которому прилегают боковые грани в форме треугольников или прямоугольников; кроме-1 012538 того, она имеет центральный элемент в виде вершины, ребра или грани, к которому также прилегают боковые грани. Когда срединный полиэдр панели спроектирован на плоскость края, каждая боковая грань спроектирована в треугольник, внутренние и внешние удвоенные углы которого равны соответственно /2- и /2+, где =/n является третьим углом треугольника, где n2 целого типа. Этим обеспечивается однозначная, непрерывная и свободная деформируемость флексора в классе полиэдральных панелей за счет нежесткой - мягкой или затянутой - потери устойчивости при плоском скольжении края панели. Размеры панели являются общими и заданными независимо, они представлены пространственными параметрами. Давайте сравним заявляемое устройство и его прототип. Мы видим, что они существенно отличаются диапазоном значений, которые может иметь угол . Формула прототипа содержит ограничение в виде =/n, где n - целое. Это нежелательное ограничение возникает поскольку модельный элементарный флексор был сконструирован с помощью правильной пирамиды. Формула данного изобретения не содержит такого ограничения, уголможет иметь любое значение в интервале (0, /2). Все другие признаки устройств совпадают, в частности это касается цели изобретения и физической причины свободной деформируемости оболочек. Для того чтобы увидеть это, достаточно рассмотреть приближенные математические изгибания срединных поверхностей полулепестков соответствующих звездчатых пирамид. Здесь мы придерживаемся следующего фундаментального принципа изометрии, сформулированного в общем виде А.В. Погореловым для общих тонких оболочек: деформация нагруженной тонкой оболочки целиком определяется соответствующим изгибанием ее срединной поверхности [9]. Указанные соответствующие изгибания описываются общими формулами, приведенными впервые в работе [10]. Они открыты не из математики, а на основании качественных положений экспериментальной механики об общем характере потери устойчивости оболочкой, изложенных А.С. Вольмиром в монографии [11]. Соответствующие обсуждения и обоснования были детально представлены в пленарном докладе автора на международной геометрической конференции [12]. Для прототипа соответствующие изгибания срединных поверхностей были открыты сначала для отдельных типов правильных пирамид. Заметим, что в заявленной формуле в качестве нового важного признака неявно заложена и определенная возможность определения допусков при технической реализации устройства; такая возможность не включена в формулу прототипа. Также заметим, что некоторые из элементов правильных пирамид - лепестков или полулепестков - могут быть использованы для построения более сложных полиэдральных панелей, которые являются модельными флексорами. Это же распространяется и на заявляемое устройство. Таким образом, мы приходим к выводу, что новая формула более общая, содержательная и полная в отличие от формулы прототипа и определяет новый класс модельных идеальных флексоров. В основу изобретения поставлена задача создания новой серии модельных флексоров в виде технологически элементарных оболочек с целью их применения для проектирования и создания конструкций с непрерывно и свободно изменяемой геометрической формой. Задача решается с помощью отдельной полиэдральной оболочки в виде четырехугольной звездчатой пирамиды, составленной из тонких упругих граней с шарнирными соединениями. Пирамида имеет две пересекающих лепестки плоскости симметрии. Указанные геометрические свойства целиком определяют пирамиду. Заметим, что в технике известны различные типы шарниров [13]: обычный цилиндрический шарнир, который носит название кинематической пары, или целая кинематическая цепь из цилиндрических шарниров; шарнир складки (узкая полоса материала оболочки); шарнир-подшипник, универсальные резиново-металлические шарниры и т.п. Какие шарниры потребуются в каждом конкретном случае будет решено после детального экспериментального и теоретического анализа инженером. На фиг. 1 показан в плане срединный полиэдр рассматриваемой оболочки заявленного устройства в форме четырехугольной звезды. Центральный элемент полиэдра - обозначенная жирной точкой вершина пирамиды А. Звезда симметрична относительно взаимно ортогональных прямых, которые вместе с тем являются линиями симметрии ее лепестков. Таким образом, каждый лепесток звезды состоит из двух равных треугольников, соприкасающихся по его диагонали, которая является проекцией выпуклого наклонного ребра пирамиды. Соседние лепестки разделены между собою сегментами, представляющими собой проекции вогнутых, наклонных ребер. Для любого из треугольников звезды его внутренний и внешний удвоенные углы, прилежащие к контуру звезды, равны соответственно /2- и /2+, гдепредставляет собой третий угол треугольника. Все указанные углы показаны на фиг. 1, где продемонстрирован только один лепесток. Соответствующие углы треугольников обозначены символамии . В общем случае эти углы ,иимеют произвольные значения из интервала (0, /2), удовлетворяя лишь естественному условию +=/2. На фиг. 2 показан план срединной поверхности сложной панели-прототипа. Панель сконструирована с помощью модельного флексора - правильной треугольной звездчатой пирамиды. Конструкция выполнена следующим образом: любая из двух граней соседних лепестков треугольной пирамиды заменяется двумя полулепестками шестиугольных звездчатых пирамид, их проекции представлены равнобедренными треугольниками; следующие две прямоугольные грани вставлены вдоль плоскости симметрии-2 012538 пирамиды. Проекции добавленных треугольников и прямоугольных граней выделены на фиг. 2 жирными линиями. Центральный элемент пирамиды - ребро АВ. Символамииобозначены соответствующие"третьи" углы треугольников звезды. Легко увидеть, что эти углы удовлетворяют равенству ==60. Символами а, b, с обозначены стороны граней треугольной пирамиды, символами r, g, s, f обозначены стороны граней шестиугольных пирамид. Исходя из формулы заявленного устройства, мы можем существенным образом варьировать конфигурацию рассматриваемой панели, а именно заменяя полулепестки треугольной пирамиды элементарного флексора полулепестками четырехугольных элементарных флексоров. Единственное условие, которое должно выполняться - углыидолжны удовлетворять следующему равенству: +=120, например =65 и =55. Тем самым возможно построение однопараметрического семейства новых сложных модельных флексоров. На фиг. 3 показан план срединной поверхности четырехугольной звездчатой пирамиды, которая является модельным флексором. Данная пирамида имеет две плоскости симметрии, которые не пересекают лепестки. Полулепестками пирамиды являются полулепестки модельных элементарных флексоров, четырехугольных звездчатых пирамид. На фиг. 3 обозначены ребра срединного полиэдра и соответствующие углыи . Двум линиям симметрии четырехугольной звезды соответствуют проекции вогнутых ребер полиэдра, центральный элемент полиэдра - вершина А. Для угловивыполняется равенство+=/2. На фиг. 4 показан план срединной поверхности модельного флексора. Оболочка получена из оболочки, представленной на фиг. 3 вставками вдоль плоскостей симметрии наклонных гранейпрямоугольников и центрального элемента, представленного на фиг. 4 прямоугольником ABCD, параллельным плоскости края пирамиды. Вставки выделены жирными линиями. Размер центрального элемента определяется выбором длин s и f соответствующих сторон прямоугольников. Суть изобретения состоит в создании элементарной подвижной конструкции, в которой реализуется уже упомянутый аксиоматический принцип геометрической теории устойчивости тонких упругих оболочек А.В. Погорелова [9]: деформационные качества технической конструкции целиком определяются характером соответствующих изгибаний ее срединной поверхности. Решение дано в виде четырехугольной звездчатой пирамиды, срединный полиэдр которой представлен на фиг. 1. Несколько более сложных модельных флексоров, представленных оболочками, построенными на базе элементов элементарной звездчатой пирамиды, их лепестков и полулепестков, но всегда с плоскими краями, показаны на фиг. 2,3, 4. Срединный полиэдр четырехугольной звездчатой пирамиды, как и срединная поверхность модельного флексора, не допускает изгибаний по О. Коши при скольжении края в плоскости [5]. В этих же условиях данный полиэдр, как и полиэдр производной модели, непрерывно изгибается с переламыванием граней около центрального элемента и вогнутых ребер или вблизи края [5]. В качестве примера, на фиг. 1 пунктиром обозначена подвижная линия слома граней одного лепестка. Подобная деформация полиэдра имеет в геометрии известное наименование - линейное изгибание [5]. Изгибание контролируется двумя параметрами: фазой, или обобщенным отклонением новых образованных вершин от старых вершин полиэдра, и амплитудой, или стрелой прогиба полиэдра. Фазу отмечает знак, "минус" показывает наличие на сгибаемом полиэдре самопересечений. На исходном этапе изгибания фаза приблизительно пропорциональная квадрату амплитуды. По классификации, принятой в аналитической теории динамических систем, такая деформация относится к нежесткой, конкретно к мягкой или затянутой, потере устойчивости; см. монографию В.И. Арнольда [14]. Описанная деформация обеспечивается соотношениями углов,предусмотренными для треугольников в плане среднего полиэдра пирамиды. Вариант потери устойчивости срединного полиэдра - мягкая или замедленная - и характер слома ребер определяются выбором его управляющих параметров, размеров пирамиды и уточняются физическим экспериментом. Технический результат. При незначительной поперечной нагрузке и скольжении края в плоскости элементарный модельный флексор представляет собой специальную четырехугольную звездчатую оболочку-пирамиду, не жестко теряющую устойчивость, и в момент бифуркации переходит в сопредельное, бесконечно близкое к начальному равновесному положению. Эти факты свидетельствуют, что в соответствии со статическим критерием Л. Эйлера панель представляет собой идеальную оболочку, которая предполагает потерю устойчивости в малом. При закритической деформации панели с медленным возмущением фазы, амплитуда растет достаточно быстро, в результате существенным образом изменяется пространственная конфигурация панели, происходит ее геометрическое изгибание в классе панелей-полиэдров. Данный феномен инициирует разнообразное использование элементов данного устройства - лепестков и полулепестков - для создания новых модельных флексоров, в частности нового типа мембран в проектировании аналога сварного металлического сильфона, сильфона как с симметричным, так и с несимметричным профилем гофров [15, 16]. Флексорность панелей, представленных на фиг. 3, 4, выявляется в тех же физических условиях и характеристиках, как и для модельного элементарного флексора. Шарнирный сильфон. Рассмотрим запертую полиэдральную оболочку с шарнирными соединениями граней, симметричную относительно определенной плоскости, элементы симметрии которой - панели, идентичные любой-3 012538 панели, изображенной на фиг. 4. Изымем у составных панелей центральные элементы. В результате, мы получаем полиэдральную оболочку, представляющую собой не что иное, как трубчатый сильфон S с одним гофром, своеобразный аналог сварного сильфона. Присоединяя шарнирами по краям сильфона S соответствующие кольцевые фланцы, будем иметь устройство, которое можно промышленно использовать как новый линзовый компенсатор - компенсатор теплового напряжения в технологических трубопроводах [15]. Собирая шарнирными соединениями пакеты сильфонов, тождественных сильфону S, будем иметь общие трубчатые гофрированные оболочки с произвольным числом гофров. Их естественно называть шарнирными сильфонами. Очевидно, шарнирные сильфоны можно использовать в качестве чувствительных элементов в точных приборах, которые действуют по принципу силовой компенсации[16]. Можно надеяться, что по своим техническим характеристикам шарнирные сильфоны по меньшей мере уравниваются со сварными. И они стойкие относительно изгибания оси, в них исключены контакты поверхностей гофров. Кроме того, они также преобладают над сварными значительно упрощенным способом изготовления и совершенным методом математического и компьютерного вычисления. Панель, представленная на фиг. 4, имеет другое важное промышленное применение. Это проектирование нового типа технических амортизаторов. Здесь ощутимый эффект будет достигаться за счет выбора для панели соответствующих упругих шарниров для соединений граней. Техническая реализация сильфона S. Материал: аустенитные или мартенситные нержавеющие стали, сплавы на основе хрома или никеля, титановые сплавы, например сталь 4X13, сплавы EI702 или 36 ХТЮ [16]; типы шарниров уточняют экспериментально. Геометрические размеры, мм: сильфон S имеет в плане симметрию относительно двух прямых; =87, b=36, с=100, r=61.3, g=56, значение s и f избираются соответственно технической задаче, длина сильфона S вдоль оси равняется 50; отклонение от истинных размеров не превосходит 0,1 мм. Теоретический свободный прогиб сильфона (рабочий ход, [16, с. 98, 129]) при растяжениисжатии незначительными нагрузками вдоль оси - почти четверть его длины. Этот результат фактически подтверждается на соответствующей модели из картона с толщиной граней 0,25 мм. Есть основания надеяться, что у сильфона S, изготовленного из конструкционного материала, рабочий ход будет порядка 10 мм. Приложение. Изучение модельного флексора ведет к открытию нового явления в механике закритически больших деформаций твердых тел. Это непосредственно проверяется на моделях, изготовленных из широко используемых материалов - картона, пластмассы, майлара и т.д. Для этих целей необходимо сконструировать реальную замкнутую полиэдральную оболочку в виде планера, который компонуется из двух экземпляров панели, показанной на фиг. 2, реальные величины параметров должны быть установлены следующими: =87, b=36, c=100, r=61.3, g=56, s=40, f=32.3. Оболочка из качественного картона, изготовленная автором в 1997 г., выдержала сотни циклов изгибаний и до сих пор находится в удовлетворительном состоянии. Литература. 1. Janos Baracs, Henry Crapo, Ivo Rosenberg et Walter Whiteley. Mathematiques et architecture. "La topologie structurale",41-42, Montreal, 1978. 2. Современные пространственные конструкции: Справочник. Под ред. Ю.А. Дыховичного и Э.З. Жуковского. Москва, "Высшая школа", 1991. 3. Современные боевые самолеты: Справ. пособие. Авт.-сост. Н.И. Рябинкин. Минск, "Элайда",1997. 4. И.Х. Сабитов. Локальная теория изгибаний поверхностей. "Итоги науки и техники. Серия: Современные проблемы математики, т. 48". Москва, ВИНИТ, 1989. 5. А.Д. Милка. Изгибания поверхностей, бифуркации динамических систем и устойчивость оболочек. Междунар. конф. "Дискр. геометрия и ее прилож.". Тезисн. докл., Москва, янв. 2001. 6. A.D. Milka. The Star-like Pyramids of A.D. Alexandrov and S.M. Vladimirova. Siberian Adv. Math.,v. 122, p. 56-72, 2002, New York, USA. 7. A.D. Milka. Bending of Surfaces, Bifurcation, Dynamical Systems and Stability of Shells. InternationalCongress of Mathematicians. Abstracts. Aug. 2002, Beijing, China. 8. Э.И. Григолюк, В.В. Кабанов. Устойчивость оболочек. Москва, "Наука", 1978. 9. А.В. Погорелов. Изгибания поверхностей и устойчивость оболочек. Киев, "Научная мысль", 1998. 10. A.D. Milka. Linear bending of star-like pyramids. C. R. Mecanique 331 (2003) 805-810, Paris, France. 11. A.C. Вольмир. Устойчивость упругих систем. Москва, "Физматгиз", 1963. 12. А.Д. Милка. Геометрия изгибаний звездчатых оболочек-бипирамид. Междунар. конф. "Геометрия в Одессе-2004. Дифференциальная геометрия и ее применения". Тезисы, докл., Одесса, май, 2004. ФОРМУЛА ИЗОБРЕТЕНИЯ Модельный элементарный флексор в виде четырехугольной звездчатой пирамиды, составленной из тонких упругих граней с шарнирными соединениями, которая имеет две плоскости симметрии, пересекающие лепестки флексора, причем каждая грань в проекции срединного полиэдра на плоскость края отображается в виде треугольника, чьи внутренний и внешний удвоенные углы, смежные с краем, равны соответственно /2- и /2+, с целью обеспечения его однозначной, непрерывной и свободной деформируемости в классе полиэдральных панелей, при плоском шарнирном скольжении края и с большими поперечными прогибами за счет нежесткой - мягкой или замедленной - потери устойчивости, отличающийся тем, что каждый из углов , третьи углы соответствующих треугольников выбираются из интервала (0, /2), и вдобавок размеры в плане и стрела подъема флексора являются его генеральными, заданными независимо параметрами.