Способ и программа моделирования физической системы с использованием объектно-ориентированного программирования
Формула / Реферат
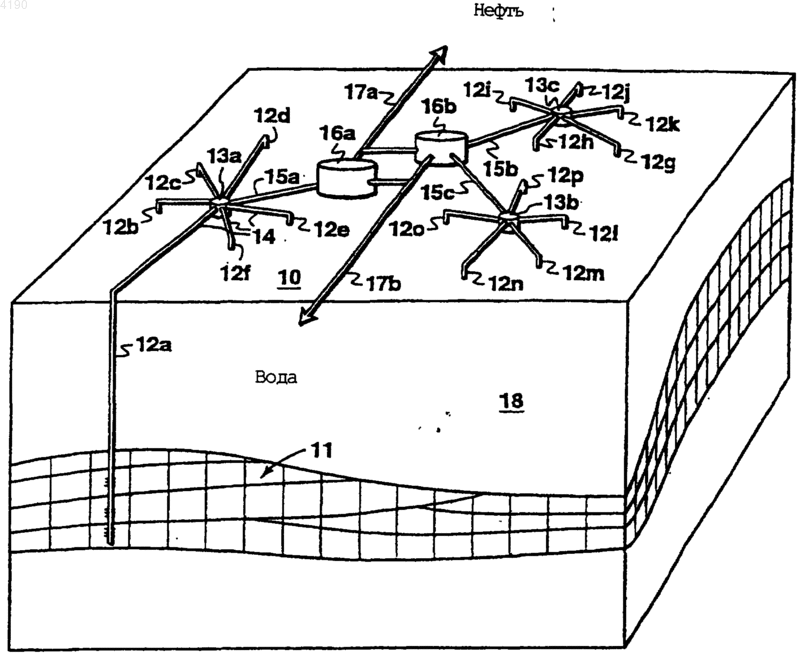
1. Способ прогнозирования свойства по меньшей мере одного флюида во флюидосодержащей физической системе, с использованием объектно-ориентированной программы, содержащий этапы, на которых формируют классы объектов моделирования, содержащие объекты группы ячеек и объекты группы соединений, и выполняют программу на компьютере для определения свойства по меньшей мере одного флюида в физической системе как функции времени.
2. Способ по п.1, отличающийся тем, что физическая система содержит углеводородосодержащую приповерхностную формацию.
3. Способ по п.1, отличающийся тем, что физическая система содержит флюидосодержащие установки, связанные с добычей углеводородов из приповерхностной углеводородосодержащей формации.
4. Способ по п.1, отличающийся тем, что физическую систему представляют посредством единичного объекта модели.
5. Способ по п.4, отличающийся тем, что физическую систему представляют посредством совокупности объектов подмодели, каждый из которых представляет часть физической системы.
6. Способ по п.1, отличающийся тем, что все ячейки группы ячеек имеют общие характеристики.
7. Способ по п.1, отличающийся тем, что все характеристики переноса для всех соединений группы соединений обрабатывают одинаковым образом.
8. Способ по п.1, отличающийся тем, что физическую систему делят на множественные домены, и программа содержит объекты группы ячеек и объекты группы соединений, связанные с ячейками и соединениями в каждом домене, и объекты группы соединений, связанные с соединениями между ячейками одного домена с ячейками другого домена.
9. Способ по п.1, отличающийся тем, что ячейки образуют неструктурированную сетку.
10. Способ по п.1, отличающийся тем, что любая ячейка из совокупности ячеек принадлежит только одному объекту группы ячеек.
11. Способ по п.1, отличающийся тем, что ячейки представляют собой ячейки сетки PEBI.
12. Способ по п.1, отличающийся тем, что ячейки являются трехмерными.
13. Способ по п.1, отличающийся тем, что сетка ячеек неструктурирована по площади и структурирована по вертикали.
14. Способ по п.1, отличающийся тем, что программу выполняют на совокупности вычислительных модулей, связанных между собой.
15. Способ по п.1, отличающийся тем, что программу выполняют на совокупности доменов с использованием совокупности ЦП.
16. Способ моделирования характеристики сложной системы с использованием объектно-ориентированной программы, содержащий этапы, на которых
a) дискретизируют физическую систему на совокупность объемных ячеек,
b) формируют совокупность соединений, представляющих перенос из ячейки в ячейку,
c) формируют совокупность объектов, задающих сложную систему, причем объекты содержат группы ячеек и группы соединений и
d) используют объекты в объектно-ориентированной программе моделирования для моделирования характеристики сложной системы.
17. Способ моделирования потока флюидов в углеводородном коллекторе и связанных с ним скважинах и установках, содержащий этапы, на которых
a) дискретизируют физическую систему на совокупность объемных ячеек,
b) распределяют объемные ячейки по группам на основании выбранных характеристик ячеек,
c) формируют объект группы ячеек, связанный с каждой группой ячеек, причем объект группы ячеек содержит информацию, необходимую для связанной с ним группы ячеек,
d) определяют соединения для потока флюида и переноса энергии между ячейками, образующими пару,
e) составляют системы уравнений, которым подчиняется поток флюидов и перенос энергии через соединения, связывающие ячейки в пары,
f) распределяют соединения, связывающие ячейки в пары, по группам, каждая из которых соединяет пару объектов группы ячеек,
g) формируют объект группы соединений, связанный с каждой группой соединений, причем объект группы соединений содержит информацию, необходимую для связанной с ним группы соединений,
h) моделируют поток флюидов и перенос энергии с использованием объектов группы ячеек и объектов группы соединений для расчета свойств флюидов, содержащихся в каждой ячейке, и для расчета потока флюидов и переноса энергии через соединения, и
i) используют результаты моделирования, полученные на этапе (h), для моделирования потока флюидов в углеводородном коллекторе и связанных с ним скважинах и установках.
18. Способ по п.17, отличающийся тем, что ячейки представляют собой ячейки сетки PEBI.
19. Способ по п.17, отличающийся тем, что ячейки являются трехмерными.
20. Способ по п.17, отличающийся тем, что сетка ячеек неструктурирована по площади и структурирована по вертикали.
21. Способ моделирования потока флюидов в углеводородном коллекторе и связанных с ним скважинах и установках, содержащий этапы, на которых
a) дискретизируют физическую систему на совокупность объемных ячеек,
b) распределяют объемные ячейки по доменам,
c) распределяют объемные ячейки в каждом домене по группам на основании выбранных характеристик ячеек,
d) формируют объект группы ячеек, связанный с каждой группой ячеек, причем объект группы ячеек содержит информацию, необходимую для связанной с ним группы ячеек,
e) определяют соединения для потока флюида и переноса энергии между ячейками, образующими пару,
f) составляют системы уравнений, которым подчиняется поток флюидов и перенос энергии через соединения, связывающие ячейки в пары,
g) распределяют соединения, связывающие ячейки в пары, по группам, каждая из которых соединяет пару объектов группы ячеек,
h) формируют объект группы соединений, связанный с каждой группой соединений, причем объект группы соединений содержит информацию, необходимую для связанной с ним группы соединений,
i) формируют объект подмодели, связанный с каждым доменом объемных ячеек, причем объект подмодели содержит группы ячеек, принадлежащие домену, и группы соединений, которые либо (1) соединяют ячейки данной группы ячеек, принадлежащей домену, с ячейками той же группы ячеек, либо (2) соединяют ячейки данной группы ячеек, принадлежащей домену, с ячейками другой группы ячеек, принадлежащей домену,
j) формируют объект модели, содержащий (1) объекты подмодели и (2) объекты группы соединений, которые соединяют ячейки данного объекта подмодели с ячейками другого объекта подмодели,
k) моделируют поток флюидов и перенос энергии с использованием объектов группы ячеек, группы соединений, подмодели, модели для расчета свойств флюидов, содержащихся в каждой ячейке, и для расчета потока флюидов и переноса энергии через соединения, и
l) используют результаты моделирования, полученные на этапе (k), для моделирования потока флюидов в углеводородном коллекторе и связанных с ним скважинах и установках.
22. Способ по п.21, отличающийся тем, что ячейки представляют собой ячейки сетки PEBI.
23. Способ по п.17, отличающийся тем, что сетка ячеек неструктурирована по площади и структурирована по вертикали.
24. Способ по п.21, отличающийся тем, что ячейки являются трехмерными.
25. Компьютерно-реализуемый способ моделирования изменяющегося во времени свойства по меньшей мере одного флюида во флюидосодержащей физической системе, содержащий этапы, на которых
a) получают и сохраняют в памяти компьютера список объектов, по меньшей мере один из которых представляет совокупность групп ячеек и совокупность групп соединений,
b) в течение заданного периода времени моделирования используют объекты в средстве моделирования для моделирования свойства по меньшей мере одного флюида в физической системе и
c) формируют выходные данные, представляющие значения свойства, изменяющегося во времени.
26. Компьютерно-считываемая среда хранения данных, материально реализующая программу по п.1 или 25, выполняемую на компьютере для осуществления способа прогнозирования свойства по меньшей мере одного флюида во флюидосодержащей физической системе, с использованием объектно-ориентированной программы, причем упомянутый способ предусматривает использование объектов группы ячеек и объектов груяяы соединений.
27. Компьютерно-считываемая среда хранения данных по п.26, отличающаяся тем, что содержит по меньшей мере одно из запоминающих устройств, а именно, ОЗУ, ПЗУ, диск, СИС и ППЗУ.
28. Компьютерная система для осуществления моделирования с использованием объектно-ориентированной программы по п.1 или 25 прогнозирования свойства по меньшей мере одного флюида во флюидосодержащей физической системе, содержащая
a) центральный процессор (ЦП),
b) пользовательский интерфейс, содержащий средство поддержки пользовательского выбора параметров моделирования в ходе выполнения программы,
c) запоминающее устройство для хранения данных и объектно-ориентированного программного кода, подключенное к ЦП для обеспечения выполнения хранящегося в нем программного кода, причем в запоминающем устройстве хранятся совокупность объектов, которая содержит совокупность групп ячеек и совокупность групп соединений, и объектно-ориентированная программа, и
d) средство осуществления моделирования для прогнозирования свойства по меньшей мере одного флюида с использованием совокупности объектов.
29. Система по п.28, отличающаяся тем, что совокупность объектов моделирования упорядочена в классы.
30. Система по п.29, отличающаяся тем, что классы содержат модель и одну или несколько подмоделей.
31. Система по п.30, отличающаяся тем, что классы дополнительно содержат одну или несколько групп ячеек и одну или несколько групп соединений.
Текст
1 Настоящее изобретение относится к способу моделирования по меньшей мере одной характеристики физической системы с использованием объектно-ориентированного программирования. В одном из аспектов изобретение относится к способу моделирования потока флюида и переноса в физической системе, содержащей, но не исключительно, по меньшей мере часть углеводородосодержащей формации. Способ особенно полезен при осуществлении параллельных расчетов при моделировании коллектора. Предшествующий уровень техники Численное моделирование широко используется в промышленности в качестве способа моделирования физической системы с использованием компьютера. В большинстве случаев желательно моделировать процессы переноса,происходящие в физической системе. В процессе переноса обычно участвуют масса, энергия,импульс или некоторые их комбинации. С использованием численного моделирования можно моделировать и наблюдать физическое явление и определять параметры конструкции, не проводя реальные лабораторные эксперименты и полевые испытания. Моделирование коллектора представляет большой интерес, поскольку оно позволяет прогнозировать поведение реального коллектора углеводородов на основании поведения модели коллектора. Обычно, целью моделирования коллектора является достаточно тщательное изучение сложных химических и физических процессов, в том числе, движений флюидов,происходящих в коллекторе, для прогнозирования поведения коллектора в будущем с целью максимизации отдачи коллектора. Под моделированием коллектора обычно понимают гидродинамику потока в коллекторе, но, в более широком смысле, моделирование коллектора можно также рассматривать как моделирование всей углеводородосодержащей системы, которая может содержать не только коллектор, но также инжекционные скважины, эксплуатационные скважины, наземные трубопроводы, сопутствующие водоносные горизонты и наземные обрабатывающие установки. Расчеты модели коллектора в таких углеводородосодержащих системах базируются на потоках флюидов по всей моделируемой углеводородосодержащей системе. Эти расчеты осуществляют с той или иной степенью строгости, в зависимости от требований конкретного модельного исследования и возможностей используемого программного обеспечения для моделирования. Принцип численного моделирования состоит в численном решении уравнений, описывающих физическое явление, с помощью компьютера. Такие уравнения обычно представляют собой обыкновенные дифференциальные уравнения и дифференциальные уравнения в частных производных. Для численного решения 2 таких уравнений используют метод конечных элементов, метод конечных разностей, метод конечных объемов и т.п. Вне зависимости от используемого метода, делят моделируемую физическую систему на ячейки (множество которых называют сеткой), и переменные состояния, изменяющиеся в пространстве на протяжении модели, выражают множествами значений для каждой ячейки. Такие свойства породы коллектора, как пористость и проницаемость,обычно полагают постоянными в пределах ячейки. Другие переменные, например, давление флюидов и насыщенность фазы, задают в определенных точках внутри ячейки, которые иногда называют узлами. Линия связи между двумя узлами называется "соединением". Поток флюида между двумя ячейками в типовом случае моделируется как поток вдоль соединения между ними. Поскольку при моделировании коллектора бывает необходимо учитывать существенно различные среды потока флюидов (например,пористая порода, скважинная труба, обрабатывающее оборудование), множество ячеек может содержать множество сегментов, отличающихся средами потоков флюидов. Хотя отдельные сегменты, например, сегменты добывающего оборудования и сегменты наземного трубопровода,можно выражать посредством одной ячейки,иногда программы моделирования коллектора разбивают такие сегменты на несколько ячеек. Составляют систему уравнений, выражающих фундаментальные законы сохранения массы, энергии и/или импульса в каждой ячейке и переноса массы, энергии и/или импульса между ячейками. Количество таких уравнений может составлять миллионы. Замена переменных состояния, изменяющихся в пространстве модели, конечным количеством значений переменных для каждой ячейки называют дискретизацией. Для анализа свойства, изменяющегося во времени, необходимо вычислять физические величины через дискретные промежутки времени, именуемые квантами времени, несмотря на то, что условия изменяются непрерывно как функция времени. Таким образом, моделирование процессов переноса, зависящих от времени,осуществляется в последовательности квантов времени. В течение кванта времени между ячейками происходит перенос того или иного рода. В процессе переноса, ячейка может обмениваться с близлежащими ячейками массой, импульсом или энергией. В пористой среде приповерхностного коллектора, перенос массы и импульса вычисляют по закону Дарси. В эксплуатационной колонне ствола скважины, расчеты переноса массы и импульса можно производить общеизвестными методами, позволяющими описывать многофазный турбулентный поток. Поток флюидов может сопровождаться конвекционным переносом энергии, который может осуще 3 ствляться сквозь породу коллектора. В некоторых случаях, учитывают также перенос энергии посредством излучения. Иногда желательно учитывать химические реакции, приводящие к выделению или поглощению массы и энергии в ячейке на протяжении кванта времени. Уравнения, которым подчиняется поведение каждой ячейки на протяжении кванта времени, объединяют в себе законы сохранения массы, импульса и энергии, которые необходимо использовать при расчете переноса. Эти уравнения могут описывать процесс переноса в неустановившемся состоянии или в установившемся состоянии. Если уравнение описывает процесс в неустановившемся состоянии, то закон сохранения можно выразить в виде: В случае процесса в квазиустановившемся состоянии, закон сохранения можно выразить следующим образом: В процессе моделирования, для каждого кванта времени, приходится решать одно или несколько громоздких матричных уравнений,количество которых зависит от используемого метода расчета с квантованием по времени. Поскольку матричные уравнения весьма громоздки(по меньшей мере, одно уравнение на ячейку),их решают методом итерации, за исключением малых моделей. Для моделирования коллекторов были предложены различные методы расчета с квантованием по времени. Два из них, получившие наиболее широкое распространение, именуются"IMPES" и полностью неявный. Согласно методу IMPES, аббревиатура которого расшифровывается как "implicit - pressure, explicit saturation" (неявное - давление, явное - насыщенность), потоки между соседними ячейками вычисляют, исходя из значений давления в конце кванта времени и значений насыщенности в начале кванта времени. Давления в конце кванта времени IMPES являются взаимозависимыми и подлежат одновременному определению. Этот метод называют неявным, поскольку каждое давление зависит от других величин (например,других давлений в конце кванта времени), которые известны лишь неявно. Основная процедура сводится к составлению матричного уравнения,в котором неявными переменными являются только давления, решению этого матричного уравнения относительно давлений, и использованию этих давлений для последовательного вычисления значений насыщенности в явном виде для всех ячеек. Таким образом, после того, 004190 4 как давления изменяются во времени, значения насыщенности обновляются в явном виде. Вычислив значения насыщенности, можно вычислять новые относительные проницаемости и капиллярные давления; они в явном виде используются в следующем кванте времени. Аналогичный подход можно использовать для других возможных искомых переменных, например, концентраций, масс компонентов, температуры или внутренней энергии. Полностью неявный метод предусматривает, что давление и насыщенность являются неявными переменными. Расходы вычисляют, исходя из фазных давлений и значений насыщенности в конце каждого кванта времени. Расчет расходов, давления и насыщенности предусматривает решение нелинейных уравнений соответствующими методами итерации. На каждой итерации составляют и решают матричное уравнение, в котором неизвестные (давление и насыщенность) изменяются в ходе итерации. После нахождения значений давления и насыщенности, обновление этих членов продолжают с использованием новых значений давления и насыщенности. Итерационный процесс заканчивается, когда выполняются заданные критерии сходимости. Метод IMPES требует сравнительно немного компьютерного времени в расчете на квант времени, но в некоторых процедурах моделирования его ограничения по стабильности вынуждают использовать большое количество малых квантов времени. Это может приводить к большим вычислительным затратам. Полностью неявный метод требует большего компьютерного времени в расчете на квант времени, по сравнению с IMPES, но позволяет использовать кванты времени значительно большего размера. Во многих процессах моделирования коллектора неявные вычисления необходимы лишь для малой доли ячеек. Были предложены программы моделирования для осуществления какIMPES, так и полностью неявных вычислений. Это дает возможность использовать длинные кванты времени, характерные для полностью неявного метода и в то же время снизить вычислительные затраты в расчете на квант времени. Дополнительную информацию по моделированию коллекторов и методам расчета можно найти в:(1) Дж. В. Уаттс, патентная заявка США 60/074188, Усовершенствованный процесс прогнозирования поведения приповерхностной формации (J.W. Watts, "Improved Process for(3) Азиз, К. и Сеттари А. Моделирование нефтяных коллекторов (Aziz К., Settari A., Pe 5(4) Д.В. Писмэн Основы численного моделирования коллекторов (D.W. Peaceman, "Fundamentals of Numerical Reservoir Simulation"), Elsevier, НьюЙорк, 1977 г.;SPE 38441, представленная на симпозиуме SPEApproach for Residual and Jacobian Array Construction in Reservoir simulations"), статья SPE 28248, представленная на конференции SPE 1994 г. по компьютеризации нефтедобычи, Даллас, Техас, 31 июля - 3 августа 1994 г. Были предприняты попытки воплотить самые разнообразные методы моделирования коллектора в единой компьютерной программе. Однако, такие универсальные системы моделирования очень сложны, в основном, из-за того,что они проектируются для обеспечения одной или более из следующих возможностей:(1) представлять большое количество разных типов ячеек (например, для разных доменов коллектора, скважинных труб, наземных установок по сбору и распределению и наземных обрабатывающих установок);(2) использовать различные методы расчета с квантованием по времени (например, IMPES, полностью неявный, последовательный неявный, адаптивный неявный и/или каскадный методы);(3) использовать разные способы представления коллекторных флюидов;(4) использовать разные способы расчета переноса между ячейками;(5) осуществлять так называемую мазутную модель, согласно которой углеводороды состоят из двух компонентов, а также осуществлять представления смеси, в которых углеводороды содержат такие соединения, как метан,этан, пропан и более тяжелые углеводороды;(6) моделировать процессы нагнетания пара или внутрипластового горения, когда необходимо учитывать изменения температуры как функцию времени, для чего требуется составлять уравнения энергетического баланса и производить сопутствующие расчеты;(7) моделировать процессы вытеснения нефти из пласта смешивающимися с ней агентами с использованием особых свойств флюидов и расчетов переноса;(8) моделировать процессы добычи углеводородов с учетом нагнетания сурфактантов,полимеров или иных агентов и втекания этих флюидов в коллектор;(9) моделировать закачку агентов, реагирующих друг с другом, углеводородами коллектора или породой коллектора; и(10) моделировать миграцию углеводородов и геологического отложения на протяжении геологического времени. В большинстве моделей коллекторов используются так называемые структурированные сетки, ячейки которых имеют трехмерные прямоугольные формы, искаженные для возможно более полного согласования с геологическими образованиями и структурами течения. Некоторые геологические образования и модельные ситуации нельзя адекватно представить в виде структурированных сеток. Этот недостаток можно частично преодолеть методом локального уточнения, согласно которому выделенные ячейки делят на ячейки меньшего размера и устанавливают непрямые соединения между ячейками, которые обеспечивают поток между ячейками, которые физически примыкают друг к другу, но не являются соседними в структуре данных. Более кардинальное решение этой проблемы заключается в том, чтобы использовать гибкость, обеспечиваемую полностью неструктурированной сеткой. Для этого требуется изменить порядок, в котором программа моделирования сохраняет свои данные и осуществляет свои вычисления. Поскольку универсальные вычисления при моделировании коллектора могут потребовать существенных вычислительных ресурсов, было предложено делить модель на сегменты меньшего размера и осуществлять параллельные расчеты на многопроцессорных компьютерах. Принципиальная привлекательность параллельных расчетов состоит в возможности сокращения времени, необходимого для построения модели, в идеале, в n раз для n-процессорного компьютера. Параллельный расчет не достигает идеала ввиду некоторых факторов, в том числе,рекурсии в решении линейных уравнений, непроизводительных затрат, связанных с передачей сообщений, необходимых для различных расчетов, и диспропорции нагрузки, обусловленных неоднородностями в физических процессах проблемы и определении характеристик углеводородных флюидов. Разработанные ранее универсальные программы моделирования используют регулярные,структурированные ячейки, характеризуемые различными типами соединений и ячеек. Эти программы моделирования по разному оперируют этими типами соединений и ячеек, что приводит к бессистемности в методологии и усложнению кода. При использовании локального уточнения такие программы дополняются непрямыми соединениями между ячейками и возможностями параллельного расчета, что делает их исключительно сложными и затрудняет их использование. Такие программы оказываются неэффективными и ненадежными. 7 В промышленности ощущается постоянная потребность в программе моделирования коллектора, которая способна осуществлять широкий круг модельных расчетов с использованием неструктурированной сетки на параллельных компьютерах. Таким образом, необходим способ, организующий и реализующий вычисления так, чтобы минимизировать сложность и, одновременно, обеспечить вычислительную эффективность. Сущность изобретения Заявлен объектно-ориентированный способ моделирования свойства по меньшей мере одного флюида во флюидосодержащей физической системе, представленной совокупностью объемных ячеек и совокупностью соединений между ячейками, предусматривающий использование объектов группа ячеек и объектов группа соединений. Изобретение может предусматривать дополнительные объекты, например, объект, содержащий всю модель, и объект,содержащий часть всей модели. Краткое описание чертежей Настоящее изобретение и его преимущества поясняются в последующем подробном описании со ссылками на чертежи, на которых подобные элементы обозначены одинаковыми позициями. Фиг. 1 А - упрощенный пример системы трехмерной структурированной сетки, содержащей шесть ячеек в направлении j, шесть ячеек в направлении i и четыре ячейки в направленииk. Фиг. 1 В - пример двумерной неструктурированной сетки, содержащей 36 ячеек. Фиг. 2 А - упрощенный пример системы трехмерной структурированной сетки, подобный примеру, приведенному на фиг. 1 А, за исключением того, что часть системы сетки разделена на дополнительные ячейки, что схематически изображено на фиг. 2 В. Фиг. 3 - упрощенный пример системы двумерной неправильной сетки, содержащей горизонтальные ряды ячеек, заканчивающиеся внутри модели. Фиг. 4 - простая схема трехмерного представления углеводородосодержащей системы,которая может быть представлена средством многоцелевого моделирования коллектора с использованием способа, отвечающего настоящему изобретению. Фиг. 5 А - упрощенная схема трехмерной структурированной сетки, подобной показанной на фиг. 1 А, которая разделена на два домена,изображенных на фиг. 5 В и 5 С. Фиг. 6 - общая иллюстрация концепции наследования в объектно-ориентированном программировании. Фиг. 7 - общая иллюстрация концепции включения в объектно-ориентированном программировании. 8 Фиг. 8 А - иллюстрация модели из восьми ячеек и фиг. 8 В - схема организации ячеек и соединений, соответствующая фиг. 8 А. Фиг. 9 - схематическая иллюстрация групп ячеек и групп соединений, сформированных из ячеек и соединений, изображенных на фиг. 8 В,которые можно использовать согласно способу,отвечающему настоящему изобретению. Фиг. 10 - схема пяти классов групп ячеек,которые можно вывести из одного базового класса. Фиг. 11 - схема, показывающая отношения наследования между классами групп соединений, в соответствии с принципами объектноориентированного программирования. Фиг. 12 - схема, показывающая отношения классов между четырьмя типами объектов, используемыми в настоящем изобретении. Фиг. 13 А - система двумерной сетки, которая разделена на четыре домена, обозначенные позициями 100-103. Фиг. 13 В - иллюстрация четырех групп ячеек, которые можно получить из домена 100. Фиг. 13 С - иллюстрация групп ячеек домена 100, показанных на фиг. 13 В, и групп ячеек доменов 101, 102, 103. В расчетах соединений в домене 100 участвуют группы ячеек, ограниченные пунктирной линией 110. Фиг. 13D - иллюстрация групп ячеек домена 100, где стрелки обозначают группы соединений, которые соединяют ячейки в группах ячеек домена 100. Фиг. 13 Е - иллюстрация групп ячеек домена 100, где стрелки обозначают группы соединений, которые соединяют ячейки между группами ячеек домена 100. Фиг. 13F - иллюстрация групп ячеек домена 100 и групп ячеек доменов 101 и 102, где стрелки обозначают группы соединений, которые соединяют ячейки домена 100 с группами ячеек доменов 101 и 102. Фиг. 14 - блок-схема высокого уровня, иллюстрирующая пример параллельной вычислительной системы, в которой используется объектно-ориентированное программирование, согласно настоящему изобретению. Чертежи не предназначены для исключения из объема изобретения других вариантов осуществления, которые являются результатом нормальных и ожидаемых модификаций этих конкретных вариантов осуществления. Подробное описание изобретения Настоящее изобретение обеспечивает новый способ моделирования физической системы, численно выражаемой посредством уравнений в частных производных. Способ можно использовать при моделировании двух- и трехмерных доменов, дискретизованных в структурированные сетки, неструктурированные сетки или их комбинацию. Способ можно также использовать в ситуациях, когда вычислительный 9 подход приводит к топологии с размерностью выше трех, что случается при моделировании потока флюидов через пористую среду с разломами. Изобретение особенно полезно при моделировании характеристики физической системы, в которой имеет место явление переноса. Термин явления переноса, используемый в этом описании, применяется в широком смысле и подразумевает перенос импульса (вязкое течение), перенос энергии (теплопроводность,конвекция и излучение) и перенос массы (диффузия). Настоящее изобретение можно применять в самых разных областях, например, в физике, определении характеристик пород, кристаллографии, электроэнергетике, биологии,математике, гидромеханике и нефтедобыче. Например, настоящее изобретение можно использовать для моделирования извлечения углеводородов из породы коллектора с использованием различных вспомогательных методов добычи, в том числе, но не только, тепловых методов добычи, в частности, операций нагнетания пара,операций нагнетания воды и методов закачивания газа, которые можно применять в условиях смешивания или отсутствия смешивания. Настоящее изобретение можно также использовать при моделировании переноса загрязнения через приповерхностные формации. Настоящее изобретение, в частности, полезно при осуществлении многоцелевого моделирования коллектора на основе систем неструктурированных сеток и особенно полезно для параллельных расчетов при моделировании углеводородосодержащих систем, которые могут включать в себя не только коллектор, но и инжекционные скважины,эксплуатационные скважины, наземные трубопроводы, сопутствующие водоносные горизонты и наземные обрабатывающие установки. Способ моделирования, отвечающий настоящему изобретению, предусматривает новый порядок сохранения расчетных данных и новый порядок вычислений. Изобретение базируется на принципах объектно-ориентированного программирования и предусматривает использование двух типов объектов программирования: один из которых представляет собой группу ячеек, а другой - группу соединений. Изобретение предусматривает возможность использования дополнительных объектов, например,объекта, содержащего всю модель, и объекта,содержащего часть всей модели. В данном описании эти четыре типа объектов будем именовать, соответственно, группа ячеек, группа соединений, модель и подмодель. Каждая группа ячеек содержит все или почти все данные, необходимые для выполнения расчетов, касающихся содержащихся в ней ячеек. Эти ячейки должны иметь определенные общие характеристики. Например, одна группа ячеек может содержать ячейки коллектора, на которых выполняются полностью неявные вычисления, а другая группа ячеек может содер 004190 10 жать ячейки коллектора, на которых выполняются вычисления IMPES. Каждая группа соединений содержит все или почти все данные, необходимые для расчетов, касающихся содержащихся в ней соединений. Поток через все эти соединения надлежит вычислять одним и тем же способом. Неограничительные примеры предусматривают, что все соединения в одной группе соединений подчиняются закону Дарси, все соединения в другой группе соединений подлежат механистическому расчету многофазного турбулентного течения, и все соединения в еще одной группе соединений подлежат расчету многофазного течения на основании заданных таблиц гидравлических параметров. Кроме того, каждое соединение в группе соединений должно связывать ячейку одной группы ячеек с другой ячейкой из той же группы ячеек или ячейку одной группы ячеек с ячейкой из другой группы ячеек. Подмодель содержит одну или несколько групп ячеек и нуль или более групп соединений,которые соединяют ячейки той или иной группы ячеек друг с другом или соединяют ячейки одной группы ячеек с ячейками другой группы ячеек, принадлежащей подмодели. Модель содержит одну или несколько подмоделей и нуль или более групп соединений, которые соединяют подмодели друг с другом. Например, если модель содержит две группы ячеек, одна из которых содержит ячейки, на которых выполняются расчеты IMPES, а другая содержит ячейки, на которых выполняются полностью неявные расчеты, то модель может содержать по меньшей мере три группы соединений, а именно: 1. соединения между ячейками в группе ячеек IMPES; 2. соединения между ячейками в полностью неявной группе ячеек; 3. соединения между ячейками группы ячеек IMPES и ячейками полностью неявной группы ячеек. Объекты модель и подмодель, в частности, пригодны для использования при параллельном осуществлении модельных расчетов . В отличие от программ моделирования,отвечающих уровню техники, которые осуществляют итерации над ячейками, способ, отвечающий настоящему изобретению, предусматривает итерации над объектами группа ячеек. При осуществлении итераций, согласно способу, отвечающему настоящему изобретению,каждый объект группа ячеек использует подходящий метод итерации и осуществляет итерации над своими ячейками, производя необходимые расчеты на каждой ячейке. Аналогично,расчеты, которые прежде производились путем итерации над соединениями, теперь производятся путем итераций над объектами группа соединений, причем каждая группа соединений пользуется своим методом итераций и осущест 11 вляет итерации над своими соединениями, производя необходимые расчеты на каждом соединении. Каждый объект группа соединений знает (т.е. располагает информацией о том),какие две группы ячеек она соединяет, или что она соединяет группу ячеек с самой собой. Аналогично, каждое соединение группы соединений знает, какие две ячейки, одна из которых принадлежит первой группе ячеек, а другая - второй группе ячеек (которая может совпадать с первой), оно соединяет. Объекты группа ячеек и группа соединений обеспечивают новый способ организации программного обеспечения, который позволяет производить обычно сложные расчеты с помощью простой, непротиворечивой структуры. Для осуществления нужных типов вычислений может понадобиться много типов групп ячеек и групп соединений. Добавление новых типов групп ячеек и групп соединений не приводит к повышению сложности структуры программы в целом. Методы вычислений, которые необходимо использовать в новых типах групп ячеек и групп соединений, инкапсулированы в соответствующих классах программного обеспечения. Объекты модель и подмодель обеспечивают способ организации особых вычислений, связанных с параллельной обработкой. Эти объекты дают возможность осуществлять параллельную обработку таким образом, чтобы минимизировать и исключить повышение сложности. По сравнению с применявшимися ранее программами моделирования преимущества настоящего изобретения можно получить, практически не теряя вычислительной эффективности. Ниже представлены основные принципы формирования ячеек и соединений, параллельных вычислений и объектно-ориентированного программирования, в целях пояснения сущности изобретения. Ячейки и соединения При практическом осуществлении способа, отвечающего настоящему изобретению, моделируемую физическую систему делят на совокупность объемных ячеек. Количество этих ячеек может составлять от десятков до миллионов. Дискретизацию осуществляют методами конечных разностей, конечных объемов, конечных элементов или аналогичными методами,основанными на делении моделируемой физической системы на сегменты меньшего размера. Данное описание настоящего изобретения, в основном, обращается к методам конечных разностей. Специалистам в данной области должно быть понятно, что изобретение можно использовать, применяя методы конечных элементов или методы конечных объемов. В случае применения методов конечных элементов, в качестве ячеек применяются конечные элементы, а в случае применения методов конечных объемов, 004190 12 в качестве ячеек применяются конечные объемы. В настоящей заявке, для простоты представления, используется термин ячейка, но следует иметь в виду, что при использовании в моделировании метода конечных элементов,термин ячейка, используемый в данном описании и формуле изобретения, следует заменить термином элемент. Вне зависимости от используемых методов, дискретизация позволяет перейти от дифференциальных уравнений в частных производных к конечномерной системе алгебраических уравнений. При практическом осуществлении данного изобретения ячейки могут иметь любую геометрическую форму, например, параллелепипедов(или кубов) или гексаэдров (обычно имеющих четыре приблизительно вертикальных угловых ребра, которые могут отличаться длиной), а также тетраэдров, ромбоидов, трапецоидов или треугольников. Сетка также может содержать прямоугольные ячейки, организованные в правильную, структурированную схему (пример которой приведен на фиг. 1 А). Структурированные ячейки имеют сходную форму и одинаковое количество сторон или граней. Чаще всего используют декартовы или радиальные структурированные сетки, в которых каждая ячейка имеет четыре стороны в двухмерном варианте или шесть граней в трехмерном варианте. Сетка также может содержать ячейки, различающиеся по форме, уложенные в неправильную, неструктурированную схему, а также может содержать совокупность структурированных и неструктурированных схем. Сетка называется гибкой или неструктурированной,если она сформирована из многоугольников(многогранников в трехмерном случае), форма,размеры и количество сторон или граней которых могут изменяться от места к месту (на фиг. 1 В показан пример двухмерной неструктурированной сетки, которая более подробно рассмотрена ниже). Могут формироваться полностью неструктурированные сетки практически любой формы. Все ячейки, предпочтительно, но не обязательно, выровнены по границам с другими ячейками, т.е. одна сторона ячейки не может контактировать со сторонами двух других ячеек. В традиционном моделировании коллекторов обычно предполагают, что большинство ячеек, представляющих коллектор, образуют структурированную, декартову сетку. На фиг. 1 А показан пример традиционного представления трехмерного домена коллектора. Это представление дает возможность идентифицировать каждую ячейку посредством набора индексов, например,(i, j, k). Пример системы декартовой сетки показан на фиг. 1 А. Согласно фиг. 1 А, с использованием системы индексов (i, j, k), ячейку, обозначенную(3, 4, 4) можно представить таким образом в компьютере. Данные, определенные на декартовой сетке, можно представлять с использованием 13 традиционных массивов, которыми оперируют большинство языков программирования; специалисты в данной области могут использовать такие массивы для представления величин,применимых к этим ячейкам. Например, давление в ячейке (i, j, k) можно представить на языке программирования Фортран как P (I, J, K), где Р- это массив действительных чисел соответствующей размерности. Удобство такого подхода в том, что можно легко узнавать значение параметра в соседних ячейках. Например, давление в шести ячейках, примыкающих к данной ячейке,выражается как P(I-1,J,K), P(I+1,J,K), P(I,J-1,K),P(I,J+1,K), P(I,J,K-1) и P(I,J,K+1), соответственно. То же справедливо для других величин, заданных в ячейках. Если возможен перенос флюида непосредственно между двумя ячейками, ячейки считают соединенными, и флюид представляют перетекающим через соединение между ними. Для этих соединений ячеек величины определяют точно так же, как и для самих ячеек. Эти величины сохраняют в массивах той же размерности, что и массивы, содержащие величины, заданные в ячейках. Например, проницаемость в направлении i между ячейкой (i, j, k) и ячейкой(i+l, j, k) можно представить как TI (I, J, K), с учетом того, что TI (NI, J, K), где NI - максимальное значение i, в действительности, не существует, поскольку это означало бы соединение ячейки с ячейкой, за пределами модели; это имеет тот же результат, что и соответствующий установке TI (NI, J, К)=0. Аналогично задают проницаемость в направлении j, TJ (I, J, K), между ячейками (i, j, k) и (i, j+1, k) и проницаемость в направлении k, TJ (I, J, K), между ячейками (i, j, k) и (i, j, k+1), которые сохраняют аналогичным образом. В языке Фортран, размеры трехмерного массива можно задавать в виде максимального разрешенного значения каждого из индексов. Например, размеры вышеупомянутого массива давления можно задать как P (NI, NJ, NK), гдеNI, NJ и NK - максимальные разрешенные значения для I, J и К, соответственно, для P (I, J, K). Фортран упорядочивает элементы массивов в памяти таким образом, что элементы, соответствующие последовательным значениям I, располагаются рядом друг с другом, элементы, соответствующие последовательным значениям J,разделяются NI элементами, и элементы, соответствующие последовательным значениям К,разделяются NINJ элементами. Значение P (I, J,K) хранится в IJK-ом элементе массива Р, гдеIJK=I+(J-l)NI+(K-1)NINJ. Хотя структурированные сетки просты в использовании, им не достает гибкости для адаптации к изменениям в коллекторе и геометрии скважины, и они часто не могут адекватно отвечать пространственным изменениям физических свойств породы и флюидов в коллекторе. Такая негибкость вносит ограничения на типы 14 углеводородосодержащих систем, которые можно эффективно представлять с помощью структурированных сеток. Для преодоления этих недостатков были предложены различные усовершенствования. Например, часто приходится использовать подробное представление одной части коллектора и более грубое представление остального коллектора. Для этого можно воспользоваться методом локального уточнения. Это значит, что прямоугольную группу ячеек заменяют сеткой более мелких ячеек. Например, применительно к системе грубой сетки, показанной на фиг. 2 А, ячейки в интервалах (i=3,4,5; j=1,2; k=2,3) можно заменить сеткой 6x4x6 более мелких ячеек, которая показана на фиг. 2 В. Как и грубая сетка (фиг. 2 А),эта локальная тонкая сетка (фиг. 2 В) также структурирована. Структурированные сетки затруднительно использовать для представления геологических слоев в коллекторе, которые выклиниваются или исчезают. На фиг. 3 показано двумерное представление слоев 50-55 ячеек, в котором слои 52 и 53 ячеек исчезают вследствие выклинивания, что дает возможность непосредственного перетока флюидов между слоями 51 и 54 ячеек. Один способ представления выклинивающихся слоев состоит в том, что соответствующие слои в модельной сетке также исчезают в этих положениях. Когда это происходит, возникает соединение между ячейками, которые обычно напрямую между собой не сообщаются. Были предложены программы моделирования,способные справляться с этой проблемой выклинивания за счет так называемых особых или непрямых соединений между ячейками. В общем случае, моделирование коллекторов углеводородосодержащих систем, содержащих значительно отличающиеся среды распространения потока флюидов, неудобно осуществлять посредством структурированных, прямоугольных сеток. Для выполнения такого моделирования необходимо обеспечить соединение между разными средами распространения потока. На фиг. 4 изображена неограничительная схема упрощенной трехмерной углеводородосодержащей системы, содержащей углеводородосодержащую формацию 11, через которую пробурены скважины 12 а-12 р (только одна скважина 12 а показана на чертеже проходящей через покрывающий слой 18 в формацию 11). Каждая скважина содержит трубу (не показана), которая обеспечивает флюидное сообщение между поверхностью земли 10 и формацией 11. Флюиды,добываемые из формации 11, проходят через скважины 12 а-р, через наземные линии сбора 14 к насосным установкам 13 а, 13b и 13 с, через дополнительные линии сбора 15 а, 15b и 15 с на наземные обрабатывающие установки 16 а и 16b,в качестве которых могут выступать традиционные водонефтяные сепараторы (для простоты 15 представления, только три из многочисленных наземных линий сбора между скважинами и насосными установками обозначены позицией 14). От обрабатывающих установок, нефть идет по линии 17 а, а вода идет по линии 17b для дальнейшей обработки и/или использования. Моделирование коллектора может предусматривать моделирование течения флюидов и смесей внутри формации 11, через скважины 12 а-р,через наземные линии сбора 14 и 15 а-с, через насосные установки 13 а-с и через обрабатывающие установки 16 а и 16b. Для выполнения моделирования углеводородосодержащей системы, при моделировании обычно предполагается, что вычисления для коллектора производятся в неустановившемся состоянии, а для установок - в квазиустановившемся состоянии. Различие двух предположений связано с количеством объемов ячейки,протекающих через ячейку в течение кванта времени. Обычно, в ячейке коллектора, объем флюида, поступающего в ячейку и выходящего из нее в течение кванта времени, составляет лишь малую долю объема ячейки. В наземной системе, напротив, через ячейку в течение кванта времени может пройти много объемов ячейки. В результате, постоянные времени, характеризующие наземную систему, обычно бывают значительно меньше тех, которые характеризуют коллектор. Наземная система достигает эффективного установившегося состояния за типичный квант времени. В ситуациях, когда структурированные сетки неэффективны, было предложено использовать гибкие сетки. Неструктурированные сетки легче согласовать с весьма разнообразными средствами распространения потока флюидов,чем структурированные сетки, и, по этой причине, неструктурированные сетки были предложены для использования при моделировании углеводородосодержащих систем. Один тип гибкой сетки, который можно использовать в способе и модели, отвечающих данному изобретению, представляет собой сетку Воронои. Ячейка Воронои, по определению,это область пространства, любая точка которой ближе к содержащемуся в этой ячейке центральному узлу, чем к любому другому узлу, и сетка Воронои состоит из таких ячеек. Каждая ячейка определяется узлом и несколькими соседними узлами. Сетка Воронои является локально ортогональной в геометрическом смысле; это значит, что границы ячейки перпендикулярны линиям, соединяющим узлы по обе стороны каждой границы. По этой причине, сетки Воронои чаще называют сетками перпендикулярных биссекций (PEBI). В некоторых случаях,можно рассматривать блок прямоугольной сетки (декартову сетку) как особый случай сеткиPEBI. Сетка PEBI обладает достаточной гибкостью, чтобы представлять весьма разнообразную геометрию коллектора, поскольку положе 004190 16 ние узлов можно выбирать произвольно. Для формирования сетки PEBI назначают местоположения узлов в данной области, после чего формируют границы ячеек таким образом, чтобы каждая ячейка содержала все точки, которые ближе к местоположению ее узла, чем к местоположению любого другого узла. Поскольку межузловые соединения в сеткеPEBI делятся пополам границами ячейки под прямым углом, это значительно упрощает решение уравнений течения для случая изотропной проницаемости (т.е., когда проницаемость одинакова во всех направлениях, хотя она может изменяться в пространстве). При этом условии такая сетка называется k-ортогональной. Для k-ортогональной сетки перенос между двумя ячейками зависит только от свойств двух ячеек и от соединения между ними. В случае анизотропной проницаемости, условие kортогональности усложняется, но, в общем случае, можно сформировать сетки, удовлетворяющие ему. Даже, когда это невозможно осуществить на практике, отклонение от kортогональности обычно невелико. В этом случае, погрешность также мала, и изменять расчеты не требуется. Если отклонение от kортогональности велико, то можно использовать аппроксимацию разветвленного потока. При использовании аппроксимации разветвленного потока, перенос между двумя ячейками зависит от свойств этих двух ячеек, а также от некоторых соседних ячеек. Для простоты, в последующем описании предполагаетсяkортогональность, но специалисты в данной области могут распространить способ, отвечающий изобретению, опираясь на идеи данного изобретения, на обработку аппроксимаций разветвленного потока. На фиг. 1 В показан пример двухмерной сетки PEBI. Точки 40 обозначают узлы ячеек,сплошные линии 41 обозначают границы ячеек,а пунктирные линии 42, соединяющие узлы,обозначают соединения между ячейками. Поток флюида, равно как и другие явления переноса между двумя узлами обычно моделируется в виде потока через соединения между ними. Сетку, образованную соединением соседних узлов ячеек PEBI, обычно называют сеткой Делони,если она состоит только из треугольников. В случае двухмерной сетки Делони, коллектор разбивается на треугольники, причем узлы совпадают с вершинами треугольников, так, чтобы треугольники заполняли коллектор. Такая триангуляция является сеткой Делони, когда окружность, проходящая через вершины треугольника (описанная окружность) не охватывает никакого другого узла. В трехмерном случае,домен коллектора разбивают на тетраэдры так,чтобы полностью заполнить объем коллектора. Такая триангуляция является сеткой Делони,когда сфера, проходящая через вершины тетраэдра (описанная сфера) не охватывает никакого 17 другого узла. Более подробное описание формирования сетки PEBI см. Палаги К.Л., Азиз К. Использование сетки PEBI в моделировании коллектора (Palagi, C.L., Aziz К.: "Use of PEBIGrid in Reservoir Simulation"), статья SPE 22889,представленная на 66-й ежегодной технической конференции и выставке, Даллас, Техас (6-9 октября 1991 г.). В расчетах с применением неструктурированных сеток можно использовать структуру данных, основанную на ячейках и соединениях. См., например, статью К.Т. Lim, D.J. Schiozer, К.Array Construction in Reservoir simulations"), SPE 28248, представленную на конференции SPE 1994 г. по компьютеризации нефтедобычи, Даллас, Техас, 31 июля - 3 августа 1994 г., в которой предлагается использовать ячейки и соединения. Размер массива давления задают равным количеству ячеек, причем давление в ячейке n обозначают Р(N). Три вышеописанных массива проницаемости объединяют в один массив, размер которого достаточно велик, чтобы вместить все значения проницаемости. Помимо этого массива, должно быть еще два целочисленных массива, указывающих, какие две ячейки имеют соединение с данной проницаемостью. Пусть,например, ячейки остаются в том же порядке, в каком они располагаются в вышеприведенном примере структурированной сетки. Тогда, в новой структуре данных, P(N) соответствует P (I,J, K), где N=I+(J-1)NI+(K-1)NINJ. Если Т (М) соответствует TK (I, J, K), то эти два целых числа принимают значенияIR(M)=N+NINJ. Способ и программа, отвечающие данному изобретению, не ограничиваются моделированием конкретной размерности. Можно создать прогнозирующую программу для одномерного(1-D), двухмерного (2-D) и трехмерного (3-D) моделирования физического домена. В приложениях моделирования коллектора, одномерная модель будет использоваться редко, поскольку она не обеспечивает моделирование по площади и по вертикали. Одномерная модель нагнетания газа для прогнозирования эффективности вытеснения не может эффективно представлять гравитационные эффекты, перпендикулярные направлению потока. Однако, одномерные модели нагнетания газа можно использовать для исследования чувствительности отдачи коллектора к изменениям параметров процесса и для интерпретации лабораторных испытаний на вытеснение. Двухмерные площадные модели закачивания жидкости можно использовать, когда в поведении коллектора преобладают площадные структуры потока. Например, площадные модели обычно используют для сравнения возможных сеток размещения скважин или для оценивания влияния неоднородности по площади на поведение коллектора. Двухмерные модели за 004190 18 качивания газа, построенные в поперечном сечении и по радиусу, можно использовать, когда в поведении коллектора преобладают структуры потока в вертикальных поперечных сечениях. Например, модели, построенные в поперечном сечении и по радиусу, обычно используют для моделирования процессов с преобладанием гравитационных эффектов, например, закачивания газа от центра к периферии или закачивания газа в коллекторы с высокой вертикальной проницаемостью, или для оценивания влияния неоднородности по вертикали на поведение коллектора. Трехмерные модели могут быть полезны для эффективного представления сложной геометрии коллектора или сложных механизмов поведения флюидов в коллекторе. Модель может представлять собой, например, трехмерную модель, содержащую слои сеток PEBI, которые в нефтяной промышленности иногда называют 21/2-D. Слоистые сетки PEBI являются неструктурированными по площади и структурированными (слоистыми) по вертикали. Построение слоистых 3-D сеток описано в (1) Heinemann,Z.E., et al., "Modeling Reservoir Geometry withIrregular Grids" (Хайнеман З.Е. и др. Моделирование геометрии коллектора с помощью неправильных сеток), SPE Reservoir Engineering,май 1991 г. и (2) Verma, S., et al., "A Control Volume Scheme for Flexible Grids in Reservoir Simulation", SPE 37999, симпозиум SPE пo моделированию коллектора, Даллас, Техас, июнь 1997 г. Параллельные вычисления Для сокращения времени, необходимого для проведения модельных расчетов, может потребоваться осуществлять моделирование параллельно на нескольких центральных процессорах. Эти ЦП могут совместно пользоваться памятью в едином блоке, или каждый из нескольких ЦП, объединенных в сеть, может иметь свою собственную память. В этих двух типах систем используются так называемые совместно используемая память и распределенная память, соответственно. Кроме того, можно объединить в сеть несколько многопроцессорных устройств, создав смешанную систему распределенной и совместно используемой памяти. Независимо от того, является ли память совместно используемой или распределенной,параллелизма в модельных расчетах достигают одним и тем же способом. Модель делят на расчетные блоки, обычно именуемые доменами. Например, если для использования доступны два центральных процессора, сеточную модель,показаннуюна фиг. 5 А, можно разделить на два домена, которые показаны на фиг. 5 В и 5 С. Это деление обычно производят так, чтобы все домены содержали, по возможности, одинаковое количество ячеек. В примере, показанном на фиг. 5 А, два домена (фиг. 5 В и 5 С) содержат в точности одинаковое количество ячеек. Каждо 19 му домену можно сопоставить один из двух центральных процессоров, и каждый центральный процессор может осуществлять практически все расчеты, относящиеся к соответствующему домену. На определенных этапах вычислений необходимо переносить данные между доменами и, следовательно, между центральными процессорами. Для этого используют так называемую пересылку сообщений. Каждую ячейку модели сопоставляют одному из двух доменов. Кроме того, каждое соединение между двумя ячейками одного домена сопоставляют этому домену. Соединения между ячейками разных доменов можно рассматривать как принадлежащие одному из доменов, принадлежащие обоим доменам или не принадлежащие ни одному из них. Согласно настоящему изобретению, предпочтительно считать междоменные соединения не принадлежащими ни одному из доменов, но используемыми обоими. В любом случае, междоменные соединения требуют иной обработки, чем внутридоменные соединения . Объектно-ориентированное программирование Способ и модель, отвечающие данному изобретению, реализуются посредством объектноориентированного программирования (ООП). Наиболее распространенными языками программирования для ООП являются Simula, Eiffel, C,Smalltalk, Objective-C или их модификации. Однако практическое применение данного изобретения не ограничивается конкретным языком ООП. Принципы построения объектно-ориентированных программ хорошо известны специалистам в области систем ООП и будут описаны лишь в общих чертах. Более подробное описание построения и работы объектно-ориентированных программ можно найти в книге "What Every Programmer(Что должен знать каждый программист об объектно-ориентированном программировании), Meiler Page-Jones, Dorset HousePublishing, New York, 1995. В объектно-ориентированной программе главная роль отводится данным, а функции, обращающиеся к этим данным, имеют второстепенное значение, в отличие от стиля программирования, в котором первичны функции, а передаваемые им данные вторичны. В отличие от программы, описываемой, в основном, посредством процедур, которым можно передавать данные и которые могут сами возвращать данные (например, программы,написанной на Фортране или Коболе), объектноориентированная программа организована вокруг объектов. Объектом является структура данных и набор операций или функций, которые могут обращаться к этой структуре данных. Системы ООП обычно содержат большое количество объектов. Каждая операция (функция), способная обращаться к структуре данных, называется методом. Каждый объект является элементом класса. Такой объект называют представителем класса, элементом которого он является. Класс зада 004190 20 ет информацию, связанную с объектом (его данные), и операции, которые он может выполнять (его методы). ООП позволяет моделировать объектами, по существу, любую сущность реального мира посредством ее характеристик,выражаемых данными, и ее поведение, выражаемое операциями, которые могут выполняться с использованием этих данных. Таким образом, объектами можно моделировать как конкретные вещи, например, ячейки в модели коллектора, так и абстрактные понятия, например,числа. Настоящее изобретение пользуется тремя преимуществами ООП, которые заключаются в его основных принципах: инкапсуляции, полиморфизма и наследования. Объекты скрывают, или инкапсулируют,внутреннюю структуру своих данных и алгоритмы выполнения своих функций. Вместо того, чтобы демонстрировать эти детали реализации, объекты представляют интерфейсы, которые отчетливо выражают их сущность, но не дают никакой посторонней информации. Интерфейс допускает лишь ограниченное количество взаимодействий между внешней средой и объектом. В программировании C, большинство взаимодействий предусматривает использование методов объекта. Используя методы объекта, внешняя среда может побуждать объект к каким-либо действиям, но подробности того, как объект осуществляет эти действия,недоступны для внешней среды. Таким образом,объект инкапсулирует свои данные и методы,скрывая их от внешней среды. Полиморфизм является следующим шагом после инкапсуляции. Компонент программного обеспечения может делать запрос другому компоненту, не имея точной информации о том, что представляет собой этот компонент. Компонент,который принимает запрос, интерпретирует его и определяет, в соответствии со своими переменными и данными, как выполнить запрос. Наследование позволяет разработчикам повторно использовать уже существующие конструкцию и код. Наследование позволяет расширять ранее написанную программу путем создания новых суперклассов и подклассов объектов. Для описания новых объектов задают их отличия от уже существующих объектов, что избавляет от необходимости заново писать программу, оперирующую новыми типами данных или функциями. Общие данные и методы принадлежат базовому классу. Более частные классы наследуют эти данные и методы и задают собственные данные и методы. Эти частные классы являются производными базового класса. Пример наследования можно проиллюстрировать с использованием классов, которые реализуют три типа многоугольников. Например, в качестве многоугольника может выступать треугольник, прямоугольник или шестиугольник. Согласно фиг. 6 эти три многоуголь 21 ника можно реализовать с использованием базового класса, а именно многоугольник 20, и трех производных классов, а именно треугольник 21, прямоугольник 22 и шестиугольник 23. Маленький треугольник 24 на фиг. 6 указывает,что классы ниже его наследуют от классов выше его. В данном примере многоугольник может представлять собой треугольник, прямоугольник или шестиугольник. Независимо от этого,он обладает площадью и цветом. Соответственно, базовый класс многоугольник содержит такие элементы данных, как площадь и цвет. Три производных класса (треугольник,прямоугольник и шестиугольник) наследуют эти элементы данных от базового класса. Кроме того, методы, одинаковые для трех производных классов, могут существовать в базовом классе. Например, метод базового класса может задавать элементы данных площадь и цвет, выделять под них память и инициализировать их. Однако вычисление площади отличается для каждого из трех типов многоугольника, поэтому каждый производный класс должен иметь собственный метод ее вычисления. Таким образом,каждый из классов, треугольник, прямоугольник и шестиугольник имеет метод, именуемый вычислениеплощади, который осуществляет операции, необходимые для расчета соответствующей площади, каковы бы эти операции ни были. Внешняя среда может содержать, например, массив объектов Многоугольник, некоторые из которых являются объектами Треугольник, некоторые - объектами Прямоугольник, а некоторые - объектами Шестиугольник. Она может получить площадь каждого из этих объектов, запросив его выполнить вычислениеплощади. Чтобы получить площадь конкретного многоугольника, внешней среде не обязательно знать, как вычисляется его площадь. Фактически, внешней среде не нужно знать даже вид многоугольника. Объекты могут содержать другие объекты. Например, чертеж может содержать многоугольники. Согласно фиг. 7, чертеж можно реализовать как объект, который является представителем класса, именуемого Чертеж 25. Этот объект может содержать объекты Многоугольник 26. Согласно фиг. 7, ромб 27 указывает, что объект более высокого класса, Чертеж 25, содержит неопределенное количество объектов более низкого класса, Многоугольник 26. В этом примере, количество объектов Многоугольник может быть равно нулю или более,поскольку Чертеж не обязан содержать многоугольник. Для объекта, внешней средой является высокоуровневый код приложения, который использует объект для выполнения своих задач. Инкапсуляция, полиморфизм и наследование позволяют коду высокого уровня оперировать 22 объектами сходных, но не идентичных, типов,как если бы они действительно были однотипными. Это значительно упрощает код высокого уровня, давая возможность написать код, который выполняет более сложные операции, чем код, написанный на процедурном языке. Расчеты ячеек и соединений Большинство модельных расчетов, производимых для каждого кванта времени, можно разделить на три категории: 1. определение свойств флюидов и переноса; 2. составление одного или нескольких матричных уравнений; и 3. решение матричного(ых) уравнения(ий). Свойства флюидов задают в ячейках и, таким образом, определяют путем итераций над ячейками. Свойства переноса относятся к соединениям, хотя некоторые из них можно задавать в ячейках. В целом, свойства переноса определяют, сочетая итерации над ячейками и над соединениями. Матричное уравнение содержит величины, заданные в ячейках, и величины, заданные на соединениях. Соответственно, его составляют, сочетая итерации над ячейками и над соединениями. Когда матричное уравнение составлено,его требуется решить. Специалистам в данной области известно много методов решения матричных уравнений. Обычно, для этого требуется производить итерации над соединениями ячейки, а также над ячейками и, возможно, над всеми соединениями. Поэтому для решения требуется дополнительная информация - список соединений каждой ячейки. Этот список можно обеспечивать в разных видах, например, в виде списка индексов недиагональных коэффициентов в строке матрицы и списка столбцов, в которых появляются эти члены. Независимо от вида списка, он должен эффективно идентифицировать каждое соединение ячейки. Объекты группа ячеек и объекты группа соединений Согласно одному варианту осуществления настоящего изобретения, используют по меньшей мере два класса объектов, заданных в соответствии с принципами объектно-ориентированного программирования: представитель одного класса содержит одну или несколько ячеек, а представитель другого класса содержит одно или несколько соединений. Другие варианты осуществления предусматривают использование дополнительных объектов, например, но не только, объекта, содержащего всю модель и/или объекта, содержащего часть всей модели. На фиг. 8 А и 8 В показан упрощенный пример ячеек и связанных с ними соединений. На фиг. 8 А изображено двухмерное представление 8 ячеек, пронумерованных от 0 до 7. Ячейки 0, 1, 4 и 5 представляют ячейки первого домена моделирования, а ячейки 2, 3, 6 и 7 представляют ячейки второго домена моделирования, 23 смежного с первым доменом. На фиг. 8 В изображено схематическое представление восьми ячеек, показанных на фиг. 8 А, и 10 соединений между ними. Показано 10 соединений (обозначенных буквами а, b, с, d, e, f, g, h, i и j). Каждое соединение изображено в виде квадрата, от которого отходят линии, ведущие к двум ячейкам,связанным этим соединением. Например, соединение а представляет собой соединение между ячейкой 0 и ячейкой 1, а соединение g представляет собой соединение между ячейкой 0 и ячейкой 4. На фиг. 9 показан пример группирования ячеек и соединений, изображенных на фиг. 8 В, в соответствии с практикой данного изобретения. Согласно фиг. 9 группа ячеек 20 содержит ячейки 0, 1, 4 и 5; группа ячеек 21 содержит ячейки 2, 3, 6 и 7. Группа соединений 30 содержит соединения a, g, h и d; группа соединений 31 содержит соединения b и е; и группа соединений 31 содержит соединения с, i, j и f. Все ячейки,входящие в группу ячеек 20 или 21, принадлежат одному домену. Группы соединений 30 и 32 состоят из соединений в пределах одного домена, а группа соединений 31 сформирована для представления множества соединений, соединяющих ячейки первого домена с ячейками второго домена. Настоящее изобретение предусматривает осуществление вычислений для разных типов ячеек в соответствии с принципами объектноориентированного программирования. Каждый тип ячейки определяют, задавая по меньшей мере три характеристики - ее физический тип, ее метод расчета и ее флюидное представление. Для моделирования коллектора каждая ячейка может относиться к одному из следующих неограничительных примеров физических типов. 1. Коллектор. Это наиболее распространенный тип ячейки. 2. Разлом. Эта ячейка может, например,представлять разлом в модели с двумя значениями пористости и двумя значениями проницаемости коллектора с разломами. 3. Скважина. В добывающей скважине флюид течет из коллектора в эту скважину. Скважина может содержать одну ячейку скважины или несколько ячеек скважины. В первом случае, флюид, поступающий в ячейку из коллектора, выходит из ячейки, перетекая в наземные установки сбора. В последнем случае, флюид перетекает из одной ячейки скважины в следующую, пока не достигнет ячейки скважины,соединенной с наземной установкой сбора. Из этой ячейки скважины флюид поступает в наземные установки сбора. 4. Труба. Ячейка трубы представляет отрезок трубы. Эта труба может входить в наземную систему сбора или представлять собой скважинную трубу, по которой добытый флюид поступает из ячейки скважины на поверхность. 24 5. Сепаратор. В сепаратор поступает один поток флюида, а выходят из него два или более потока. Обычно сепаратор отделяет воду от углеводорода или жидкий углеводород от газообразного углеводорода. Возможны и другие типы ячеек, и данное изобретение не ограничивается вышеприведенными примерами. Специалисты в данной области могут разработать дополнительные типы ячеек, пригодные для конкретного прикладного моделирования. На фиг. 10 показаны пять классов, представленные блоками 61, 62, 63, 64 и 65, которые основаны на вышеперечисленных пяти типах ячеек, и которые можно вывести из одного базового класса, который называется Группаячеек 60. Группаячеек 60 содержит данные и процедуры, общие для пяти производных классов 61, 62, 63, 64 и 65. Каждый из производных классов (например, класс 61, Группаячеекколлектора) содержит данные и методы, присущие только этому классу. Треугольник 66, изображенный на фиг. 10, обозначает наследование в том смысле, в каком этот термин используется в объектно-ориентированном программировании. Это значит, что данные и способы, общие для пяти производных классов (6165), следует задавать только в базовом классе,Группаячеек 60. Метод расчетов следует выбирать для каждой ячейки. В качестве методов расчета предпочтительно использовать, в том числе, следующие: 1. IMPES; 2. полностью неявный. Метод расчета можно осуществлять одинаково для вышеописанных пяти производных классов. В результате, метод расчета и данные,необходимые для расчетов, можно размещать в базовом классе, Группаячеек 60. Каждый из пяти производных классов (классы 61-65) будут наследовать метод расчета от класса Группаячеек 60. Флюидное представление ячейки задают,указывая имеющиеся компоненты, учитывая или не учитывая энергию, и указывая метод вычисления свойств. Одна часть модели может представлять флюиды коллектора одним набором компонентов, а другая часть может представлять флюиды вторым набором компонентов. Альтернативно, в одной части модели можно производить расчет баланса энергии, а в другой - не производить. Для данного набора компонентов свойства можно вычислять разными методами. Ниже приведен неограничительный список возможных методов вычисления свойств. 1. Нефть-вода/мазутный метод. 2. Нефть-газ/мазутный метод. 3. Газ-вода/мазутный метод. 4. Нефть-газ-вода/мазутный метод. 25 5. Нефть-вода/тепловой метод. Вода может быть в жидкой фазе или в газообразной фазе(например, в виде пара). 6. Нефть-газ-вода/тепловой метод. 7. Уравнение состояния для данного состава. 8. Равновесное значение для данного состава. 9. Уравнение состояния для данного состава/тепловой метод. 10. Равновесное значение для данного состава/тепловой метод. Как и рассмотренный выше метод расчета,вычисления свойств флюидов можно реализовать в базовом классе, Группаячеек 60, изображенном на фиг. 10. Каждый объект группа ячеек объединяет по одному варианту выбора для каждой из трех категорий характеристик ячейки. Пусть, например, объект группа ячеек относится к физическому типу скважина, его метод расчета - полностью неявный, и в его флюидном представлении используется нефть-газ-вода/мазутный метод. Тогда он будет содержать полностью неявные ячейки скважины, в которых свойства флюидов определяются путем расчетов мазутным методом с использованием компонентов нефть, вода и газ. Первые шесть типов вышеперечисленных групп ячеек характеризуются набором компонентов, которые являются компонентами, используемыми в этих шести типах. Последние четыре не характеризуются таким набором; их набор компонентов задан как часть входных данных модели. Для последних четырех типов групп ячеек, количество компонентов и их наименование может варьироваться от одной группы ячеек к другой, но в пределах данной группы ячеек они должны быть фиксированы. В вышеприведенном примере может существовать 5x2x10, т.е. 100 возможных комбинаций физических типов ячейки, методов расчета и флюидных представлений, но для их реализации требуются только один базовый класс и пять производных классов. Кроме того, в силу использования наследования, производные классы обязаны реализовать только им одним присущие особенности. Выведение всех классов групп ячеек из одного базового класса дает возможность полиформно оперировать ими. Например, в C, код более высокого уровня, который содержит группы ячеек, может обращаться к ним посредством массива указателей на базовый класс,Группаячеек 60. Это дает возможность коду более высокого уровня использовать объекты,не зная, к каким конкретным видам групп ячеек они относятся. Если используются множественные объекты группа ячеек, то используются также множественные объекты группа соединений. Каждое соединение в модели следует помещать в одну из групп соединений. Каждая группа со 004190 26 единений соединяет либо две группы ячеек, либо группу ячеек с самой собой. Каждая группа соединений осуществляет определенный тип расчета переноса. Каждый тип группы соединений может соединять только определенные типы групп ячеек. Например, было бы неправильно соединять две ячейки коллектора посредством соединения многофазного турбулентного потока. С другой стороны, данный тип группы соединений может соединять несколько типов групп ячеек. Например, группа соединений многофазного турбулентного потока может соединять группу ячеек коллектора с группой ячеек наземного сбора, группу ячеек наземного сбора с самой собой или группу ячеек наземного сбора с группой ячеек сепаратора. Каждый тип групп соединений определяют, задавая по меньшей мере три свойства: (1) метод вычисления переноса флюидов, (2) типы расчетов для групп ячеек, который он соединяет, и (3) возможность соединения групп ячеек,которые используют разные наборы компонентов. Ниже приведены неограничительные примеры принципов расчета переноса, которые все относятся к физическим типам ячеек. 1. Закон Дарси с использованием таблицы поиска без гистерезиса. Применим, например, к потоку между ячейками в коллекторе. 2. Закон Дарси с использованием таблицы поиска с гистерезисом. Применим, например, к потоку между ячейками коллектора. 3. Закон Дарси с использованием степенных уравнений. Применим, например, к потоку между ячейками коллектора. 4. Поток из разлома в разлом. 5. Поток из коллектора в разлом. 6. Механистический многофазный турбулентный поток. Применимо, например, к потоку из скважины в скважину, из скважины в трубу,из трубы в трубу и из трубы в сепаратор. 7. Многофазный поток с использованием табличных расчетов. Применим, например, к потоку из скважины в скважину, из скважины в трубу, из трубы в трубу и из трубы в сепаратор. 8. Поток из коллектора в скважину. 9. Поток из разлома в скважину. Неограничительные примеры типов расчета соединенных групп ячеек включают в себя: 1. IMPES-IMPES; 2. полностью неявный - полностью неявный; 3. IMPES - полностью неявный. Исходя из флюидных представлений, используемых в соединенных группах ячеек,флюидные представления в группах ячеек можно представить как: 1. одно и то же флюидное представление,используемое в обеих группах ячеек, или 2. разные флюидные представления, используемые в двух группах ячеек. 27 На фиг. 11 схематически изображены классы, необходимые для реализации девяти возможных вариантов потока для девяти вышеперечисленных физических типов ячеек и отношения наследования между полученными классами. Базовый класс, изображенный на фиг. 11 блоком 70 и именуемый Группасоед, может содержать общие данные и реализовать общие функции для следующих трех классов. 1. Bce потоки коллектор-коллектор, коллектор-разлом и разлом-разлом. Этот класс можно назвать Группасоедколкол, который изображен на фиг. 11 блоком 71. 2. Потоки коллектор-скважина и разломскважина. Этот класс можно назвать Группасоедколскв, который изображен блоком 72. 3. Потоки в пределах сети установок. Этот класс можно назвать Группасоедустуст, который изображен блоком 73. Согласно фиг. 11, класс Группасоедколкол(блок 71) должен существовать в трех вариантах; один вариант осуществляет тип расчета полностью неявный - полностью неявный (блок 74), другой осуществляет тип расчета IMPES-IMPES (блок 75), и еще один осуществляет тип расчета IMPES полностью неявный (блок 78). В сети установок(блок 73) осуществляются только полностью неявные расчеты по причине ограничений по стационарности, присущие методу IMPES. Поэтому для класса Группасоедустуст требуется только вариант полностью неявный полностью неявный. Треугольники 80, 81 и 82 указывают, что более низкие классы наследуют от более высоких классов. Кроме того, в случае расчетов тепловых эффектов необходимо производить расчеты переноса энергии. Конвекционный перенос энергии можно рассматривать по аналогии с конвекционным переносом массы. Поскольку возможен также перенос энергии путем теплопроводности, при желании, можно включить также расчеты теплопроводности, в частности, для соединений, внутренних по отношению к коллектору. В других типах соединений, конвекционный перенос энергии может доминировать, и в этом случае включать расчеты теплопроводности нецелесообразно. Конвекционный перенос энергии обычно считают настолько сходным с конвекционным переносом массы, что их расчет не нужно производить по отдельности. Перенос энергии за счет теплопроводности необходимо рассчитывать отдельно, поэтому каждый из девяти вышеперечисленных типов расчета переноса может, в принципе, предусматривать расчет теплопроводности; однако на практике расчет теплопроводности требуется только в коллекторе. Способ, отвечающий настоящему изобретению, может также включать в себя расчеты,связанные с химическими реакциями. В отсутствие химических реакций, сохранение массы 28 фактически эквивалентно сохранению химических соединений. При наличии химических реакций, ввиду синтеза и распада соединений,сохранение массы эквивалентно сохранению элементов. Химические реакции могут приводить к выделению или поглощению энергии. Учет химических реакций не требует изменения способа, отвечающего настоящему изобретению. Он требует только добавления новых типов групп ячеек и групп соединений, которые специалисты в данной области могут добавить,опираясь на идеи, изложенные в этом описании. В вышеизложенном описании данного изобретения описано использование только двух типов объектов: групп ячеек и групп соединений. Согласно другому варианту осуществления изобретения, способ предусматривает дополнительно один или несколько объектов подмодель и один или несколько объектов модель. Эти объекты выступают в качестве контейнеров для групп ячеек и групп соединений. Объект подмодель содержит один или несколько объектов группа ячеек и нуль или более объектов группа соединений. Любые группы соединений в подмодели соединяют либо ячейки одной из групп ячеек подмодели с ячейками той же группы ячеек, либо ячейки одной из групп ячеек подмодели с ячейками другой группы ячеек подмодели. Объект модель содержит один или несколько объектов подмодель и нуль или более объектов группа соединений, каждый из которых соединяет группу ячеек одной подмодели модели с группой ячеек другой подмодели модели. Группы соединений, внутренние по отношению к подмодели, невидимы для модели. На фиг. 12 показана упрощенная схема отношений включения для классов, именуемых Модель 85, Подмодель 86, Группаячеек 87 и Группасоед 88. Ромбовидные символы 89, 90,91 и 92 обозначают включение в том смысле, в каком этот термин используется в объектноориентированном программировании. Согласно фиг. 12, Модель 85 может содержать один или несколько объектов Подмодель 86. При наличии только одного объекта Подмодель 86 не существует объекта Группасоед 88, содержащегося непосредственно в объекте Модель 85. При наличии двух или более объектов Подмодель 86 и соединений между ними, объект Модель 85 содержит один или несколько объектов Группасоед 88. Каждый объект Подмодель 86 содержит по меньшей мере один объект Группаячеек 87. Объект Подмодель 86 не обязан содержать какой-либо объект Группасоед 88. На фиг. 13 А показан физический домен,разделенный на четыре пространственных домена 100, 101, 102 и 103. Каждый домен содержит ячейку и данные соединения. При составлении уравнений моделирования используются три основных типа вычислений: только для ячейки, только для соединения и ячейка 29 соединение-ячейка. Вычисления только для ячейки и только для соединения являются независимыми и могут выполняться параллельно без привлечения совместно используемой информации. Вычисления ячейка-соединениеячейка по границе между двумя доменами требуют информации из двух доменов. Например,перепад давлений от одной ячейки к другой,соединенной с ней ячейке является количественным параметром соединения и может быть вычислен как:dp(соединение)=р(левая ячейка)-р(правая ячейка) Требуются данные по обе стороны соединения, поэтому такое вычисление относится к типу ячейка-соединение-ячейка. Соединению приписывают левую и правую стороны. Поток слева направо считают положительным. Вычисление типа ячейка-соединение-ячейка,подобное вышеописанному, удобно осуществлять путем итераций над соединениями группы соединений. Если данные ячейки с одной стороны соединения не содержатся в данном домене,то данные ячейки следует получать из соседнего домена. В предыдущем абзаце предполагается наличие k-ортогональной сетки, поскольку в процессе вычисления участвуют только две соединенные ячейки. В случае использования аппроксимации разветвленного потока, в процессе вычисления должны участвовать и другие соседние ячейки. Группа соединений должна иметь информацию о том, какие соседние ячейки связаны каждым из ее соединений, а также должна содержать другую информацию. Специалистам в данной области не составит труда расширить настоящее изобретение для включения этой дополнительной информации, исходя из идей, изложенных в данной заявке. Такое расширение предусматривает возможность того, что соединение может задействовать более двух групп ячеек. Это значит, что вместо наличия по меньшей мере одной группы соединений для каждой соединенной пары групп ячеек, предусмотрено наличие по меньшей мере одной группы соединений аппроксимации разветвленного потока для каждого уникального набора групп ячеек,участвующих в расчете соединения. В соответствии с этими требованиями, домен можно разделить на группы данных ячейки и данных соединения. Для определенных расчетов соединения требуется информация ячеек из соседних доменов. В примере, показанном на фиг. 13 А, предусмотрено наличие соединений только между доменами 100 и 101, 100 и 102,101 и 103, 102 и 103 и отсутствие соединений ячеек между доменами 100 и 103 и между доменами 102 и 101. Внутри домена ячейки и соединения делятся на различные группы ячеек. Группа ячеек состоит из всех ячеек, участвующих в расчетах соединения для конкретного множества доменов. Домен 100 можно разделить на четыре 30 группы ячеек 100 а, 100b, 100 с и 100d, которые схематически изображены на фиг. 13 В. В домене 100, например, группа ячеек 100 а представляет собой множество всех ячеек, соединенных только с ячейками домена 100. Группа ячеек 100b представляет собой множество всех ячеек,соединенных только с ячейками домена 101. Группа ячеек 100 с представляет собой множество всех ячеек, соединенных только с ячейками домена 102. Группа ячеек 100d представляет собой множество всех ячеек, соединенных с ячейками доменов 101 и 102. Каждая ячейка принадлежит только одной группе ячеек. На фиг. 13 С схематически изображены четыре группы ячеек для каждого из четырех доменов 100, 101, 102 и 103 (группы ячеек 100 а, 100b,100 с и 100d для домена 100; группы ячеек 101a,101b, 101 с и 101d для домена 101; группы ячеек 102 а, 102b, 102 с и 102d для домена 102; и группы ячеек 103 а, 103b, 103 с и 103d для домена 103). В расчетах соединений в домене 100 участвуют все группы ячеек домена 100 и некоторые группы ячеек доменов 101 и 102. Такие группы ячеек домена 100 показаны на фиг. 13 С обведенными пунктирной линией 110. Для расчетов соединений внутри домена соединения разделяют на множество групп соединений. Каждой группе ячеек, связанной с определенным доменом, соответствует группа соединений, соединяющая ячейки данной группы ячеек с другими ячейками той же группы ячеек (предполагаем, что такие соединения существуют). Для домена 100 они обозначены на фиг. 13D стрелками 200, 201, 202 и 203. Другие группы соединений соединяют ячейки одной группы ячеек с ячейками другой группы ячеек, что изображено стрелками 204,205, 206 и 207 на фиг. 13 Е. Дополнительные группы соединений соединяют группы ячеек одного домена с группами ячеек другого домена. Согласно фиг. 13F,группы ячеек 100b и 100d домена 100 соединены с группами ячеек 101b и 101d домена 101,что изображено стрелками 208 и 209, и группы ячеек 100 с и 100d домена 100 соединены с группами ячеек 102 с и 102d домена 102, что изображено стрелками 211 и 210. Всю сетку, представляющую домены, изображенные на фиг. 13 А, можно представить посредством объекта Модель 85, изображенного на фиг. 12. Объект Модель 85 содержит четыре объекта Подмодель 86, каждый из которых представляет один из четырех доменов (100,101, 102 и 103). Объект Модель 85 содержит также восемь объектов Группасоед 88: два,соединяющих домен 100 с доменом 101, два,соединяющих домен 100 с доменом 102, два,соединяющих домен 101 с доменом 103, и два,соединяющих домен 102 с доменом 103. Каждый объект Подмодель 86 содержит четыре объекта Группаячеек. Для домена 100 эти подгруппы показаны на фиг. 13 В. Ячейки группы 31 100 а соединены только с ячейками домена 100,ячейки группы 100b соединены с ячейками домена 101, а также с ячейками домена 100, ячейки 100 с соединены с ячейками домена 102, а также домена 100, и ячейки группы 100d соединены с ячейками доменов 101 и 102, а также с ячейками домена 100. Ячейки групп 100b, 100 с и 100d - это ячейки, данные которых требуются доменам 101 и/или 102. Домену 100 требуются данные аналогичных групп ячеек в доменах 101 и 102. На фиг. 13F эти группы ячеек обозначены штриховкой. На фиг. 14 показана схема системы аппаратного и программного обеспечения настоящего изобретения. Система содержит один или несколько вычислительных модулей 200 и 201,дисплейный терминал 203 и энергонезависимое запоминающее устройство 204. Каждый вычислительный модуль содержит два энергозависимых запоминающих устройства 205 и 206,обычно это оперативная память (ОЗУ), для обеспечения оперативного хранения объектноориентированной программы 207 (установленной на обоих вычислительных модулях 200 и 201), активных данных и промежуточных результатов, и один или несколько центральных процессоров (ЦП) для осуществления расчетов,касающихся одного или нескольких доменов. Исключительно в целях иллюстрации, показаны только два расчетных домена 208 и 209 для вычислительного модуля 200 и два расчетных домена 210 и 211 для вычислительного модуля 201. Согласно фиг. 14, два ЦП 217 и 218 связаны с вычислительным модулем 200 и два ЦП 219 и 220 связаны с вычислительным модулем 201. Вычислительные модули 200 и 201 могут представлять собой универсальные компьютеры, миникомпьютеры, рабочие станции или персональные компьютеры. В случае использования при практическом осуществлении изобретения более одного вычислительного модуля,вычислительные модули можно связывать между собой высокоскоростными линиями связи,которые на фиг. 14 символически представлены соединением, обозначенным позицией 225. Энергонезависимое запоминающее устройство 204 используется для постоянного хранения объектно-ориентированной программы 207 и данных. Оно обычно содержит запоминающее устройство прямого доступа (ЗУПД), а также может содержать накопитель на магнитной ленте, привод перезаписываемого оптического диска и другие общеизвестные устройства. Дисплейный терминал 203 может содержать экран или иное устройство визуального отображения информации, а также клавиатуру. Настоящее изобретение может быть реализовано в виде программного обеспечения или в виде сочетания программного и аппаратного обеспечения. В случае полной или частичной программной реализации, изобретение может быть реализовано, постоянно или временно, на(ПЗУ), на диске или дисках, в специализированной интегральной схеме (СИС), в перезаписываемой постоянной памяти (ППЗУ) и т.д. Выше описаны принцип настоящего изобретения и оптимальные варианты применения этого принципа. Специалистам в данной области очевидно, что вышеописанные варианты осуществления допускают различные изменения, не выходящие за рамки сущности и объема изобретения, определяемые прилагаемой формулой изобретения. Поэтому следует понимать,что данное изобретение не ограничивается показанными и описанными выше конкретными деталями. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ прогнозирования свойства по меньшей мере одного флюида во флюидосодержащей физической системе, с использованием объектно-ориентированной программы, содержащий этапы, на которых формируют классы объектов моделирования, содержащие объекты группы ячеек и объекты группы соединений, и выполняют программу на компьютере для определения свойства по меньшей мере одного флюида в физической системе как функции времени. 2. Способ по п.1, отличающийся тем, что физическая система содержит углеводородосодержащую приповерхностную формацию. 3. Способ по п.1, отличающийся тем, что физическая система содержит флюидосодержащие установки, связанные с добычей углеводородов из приповерхностной углеводородосодержащей формации. 4. Способ по п.1, отличающийся тем, что физическую систему представляют посредством единичного объекта модели. 5. Способ по п.4, отличающийся тем, что физическую систему представляют посредством совокупности объектов подмодели, каждый из которых представляет часть физической системы. 6. Способ по п.1, отличающийся тем, что все ячейки группы ячеек имеют общие характеристики. 7. Способ по п.1, отличающийся тем, что все характеристики переноса для всех соединений группы соединений обрабатывают одинаковым образом. 8. Способ по п.1, отличающийся тем, что физическую систему делят на множественные домены, и программа содержит объекты группы ячеек и объекты группы соединений, связанные с ячейками и соединениями в каждом домене, и объекты группы соединений, связанные с соединениями между ячейками одного домена с ячейками другого домена. 33 9. Способ по п.1, отличающийся тем, что ячейки образуют неструктурированную сетку. 10. Способ по п.1, отличающийся тем, что любая ячейка из совокупности ячеек принадлежит только одному объекту группы ячеек. 11. Способ по п.1, отличающийся тем, что ячейки представляют собой ячейки сетки PEBI. 12. Способ по п.1, отличающийся тем, что ячейки являются трехмерными. 13. Способ по п.1, отличающийся тем, что сетка ячеек неструктурирована по площади и структурирована по вертикали. 14. Способ по п.1, отличающийся тем, что программу выполняют на совокупности вычислительных модулей, связанных между собой. 15. Способ по п.1, отличающийся тем, что программу выполняют на совокупности доменов с использованием совокупности ЦП. 16. Способ моделирования характеристики сложной системы с использованием объектноориентированной программы, содержащий этапы, на которыхa) дискретизируют физическую систему на совокупность объемных ячеек,b) формируют совокупность соединений,представляющих перенос из ячейки в ячейку,c) формируют совокупность объектов, задающих сложную систему, причем объекты содержат группы ячеек и группы соединений, иd) используют объекты в объектноориентированной программе моделирования для моделирования характеристики сложной системы. 17. Способ моделирования потока флюидов в углеводородном коллекторе и связанных с ним скважинах и установках, содержащий этапы, на которыхa) дискретизируют физическую систему на совокупность объемных ячеек,b) распределяют объемные ячейки по группам на основании выбранных характеристик ячеек,c) формируют объект группы ячеек, связанный с каждой группой ячеек, причем объект группы ячеек содержит информацию, необходимую для связанной с ним группы ячеек,d) определяют соединения для потока флюида и переноса энергии между ячейками,образующими пару,e) составляют системы уравнений, которым подчиняется поток флюидов и перенос энергии через соединения, связывающие ячейки в пары,f) распределяют соединения, связывающие ячейки в пары, по группам, каждая из которых соединяет пару объектов группы ячеек,g) формируют объект группы соединений,связанный с каждой группой соединений, причем объект группы соединений содержит информацию, необходимую для связанной с ним группы соединений, 004190h) моделируют поток флюидов и перенос энергии с использованием объектов группы ячеек и объектов группы соединений для расчета свойств флюидов, содержащихся в каждой ячейке, и для расчета потока флюидов и переноса энергии через соединения, иi) используют результаты моделирования,полученные на этапе (h), для моделирования потока флюидов в углеводородном коллекторе и связанных с ним скважинах и установках. 18. Способ по п.17, отличающийся тем, что ячейки представляют собой ячейки сетки PEBI. 19. Способ по п.17, отличающийся тем, что ячейки являются трехмерными. 20. Способ по п.17, отличающийся тем, что сетка ячеек неструктурирована по площади и структурирована по вертикали. 21. Способ моделирования потока флюидов в углеводородном коллекторе и связанных с ним скважинах и установках, содержащий этапы, на которыхa) дискретизируют физическую систему на совокупность объемных ячеек,b) распределяют объемные ячейки по доменам,c) распределяют объемные ячейки в каждом домене по группам на основании выбранных характеристик ячеек,d) формируют объект группы ячеек, связанный с каждой группой ячеек, причем объект группы ячеек содержит информацию, необходимую для связанной с ним группы ячеек,e) определяют соединения для потока флюида и переноса энергии между ячейками,образующими пару,f) составляют системы уравнений, которым подчиняется поток флюидов и перенос энергии через соединения, связывающие ячейки в пары,g) распределяют соединения, связывающие ячейки в пары, по группам, каждая из которых соединяет пару объектов группы ячеек,h) формируют объект группы соединений,связанный с каждой группой соединений, причем объект группы соединений содержит информацию, необходимую для связанной с ним группы соединений,i) формируют объект подмодели, связанный с каждым доменом объемных ячеек, причем объект подмодели содержит группы ячеек,принадлежащие домену, и группы соединений,которые либо (1) соединяют ячейки данной группы ячеек, принадлежащей домену, с ячейками той же группы ячеек, либо (2) соединяют ячейки данной группы ячеек, принадлежащей домену, с ячейками другой группы ячеек, принадлежащей домену,j) формируют объект модели, содержащий(1) объекты подмодели и (2) объекты группы соединений, которые соединяют ячейки данного объекта подмодели с ячейками другого объекта подмодели, 35k) моделируют поток флюидов и перенос энергии с использованием объектов группы ячеек, группы соединений, подмодели, модели для расчета свойств флюидов, содержащихся в каждой ячейке, и для расчета потока флюидов и переноса энергии через соединения, иl) используют результаты моделирования,полученные на этапе (k), для моделирования потока флюидов в углеводородном коллекторе и связанных с ним скважинах и установках. 22. Способ по п.21, отличающийся тем, что ячейки представляют собой ячейки сетки PEBI. 23. Способ по п.17, отличающийся тем, что сетка ячеек неструктурирована по площади и структурирована по вертикали. 24. Способ по п.21, отличающийся тем, что ячейки являются трехмерными. 25. Компьютерно-реализуемый способ моделирования изменяющегося во времени свойства по меньшей мере одного флюида во флюидосодержащей физической системе, содержащий этапы, на которыхa) получают и сохраняют в памяти компьютера список объектов, по меньшей мере один из которых представляет совокупность групп ячеек и совокупность групп соединений,b) в течение заданного периода времени моделирования используют объекты в средстве моделирования для моделирования свойства по меньшей мере одного флюида в физической системе иc) формируют выходные данные, представляющие значения свойства, изменяющегося во времени. 26. Компьютерно-считываемая среда хранения данных, материально реализующая программу по п.1 или 25, выполняемую на компьютере для осуществления способа прогнозирования свойства по меньшей мере одного флюида во флюидосодержащей физической системе, с использованием объектно-ориентированной программы, причем упомянутый способ предусматривает использование 36 объектов группы ячеек и объектов группы соединений. 27. Компьютерно-считываемая среда хранения данных по п.26, отличающаяся тем, что содержит по меньшей мере одно из запоминающих устройств, а именно, ОЗУ, ПЗУ, диск,СИС и ППЗУ. 28. Компьютерная система для осуществления моделирования с использованием объектно-ориентированной программы по п.1 или 25 прогнозирования свойства по меньшей мере одного флюида во флюидосодержащей физической системе, содержащаяa) центральный процессор (ЦП),b) пользовательский интерфейс, содержащий средство поддержки пользовательского выбора параметров моделирования в ходе выполнения программы,c) запоминающее устройство для хранения данных и объектно-ориентированного программного кода, подключенное к ЦП для обеспечения выполнения хранящегося в нем программного кода, причем в запоминающем устройстве хранятся совокупность объектов, которая содержит совокупность групп ячеек и совокупность групп соединений, и объектноориентированная программа, иd) средство осуществления моделирования для прогнозирования свойства по меньшей мере одного флюида с использованием совокупности объектов. 29. Система по п.28, отличающаяся тем,что совокупность объектов моделирования упорядочена в классы. 30. Система по п.29, отличающаяся тем,что классы содержат модель и одну или несколько подмоделей. 31. Система по п.30, отличающаяся тем,что классы дополнительно содержат одну или несколько групп ячеек и одну или несколько групп соединений.
МПК / Метки
МПК: G06F 9/455
Метки: программирования, программа, системы, объектно-ориентированного, использованием, физической, моделирования, способ
Код ссылки
<a href="https://eas.patents.su/21-4190-sposob-i-programma-modelirovaniya-fizicheskojj-sistemy-s-ispolzovaniem-obektno-orientirovannogo-programmirovaniya.html" rel="bookmark" title="База патентов Евразийского Союза">Способ и программа моделирования физической системы с использованием объектно-ориентированного программирования</a>
Предыдущий патент: Способы и устройство для управления трафиком интернет-протокола в глобальной или локальной сети
Следующий патент: Теплоизоляционное и/или звукоизоляционное изделие на основе минеральной ваты
Случайный патент: Способ получения эзетимиба и его производных












