Способ создания анизотропной петрофизической вычислительной модели подземной области
Формула / Реферат
1. Способ создания анизотропной петрофизической вычислительной модели подземной области, моделирующей анизотропию глинистых сланцев и анизотропию, обусловленную напряжением, и имеющей объем пор, глинистость и объем песка, в котором измеряют давление вышележащей породы и глинистости в подземной области, разделяют объем пор модели на поры глины, поры песка и микротрещины, выбирают математические отношения, при которых разделение объема пор на три части может быть выполнено количественно на основе оценок давления вышележащей породы и глинистости в подземной области, смешивают песчаные зерна с частицами глины в модели с использованием первого закона смешивания, добавляют смоченные поры глины с предпочтительным распределением ориентации к относящейся к глине части объема пор модели, добавляют пустые поры песка и выровненные микротрещины, соответственно, к частям песка и микротрещин объема пор модели, смешивают углеводороды с водой с использованием второго закона смешивания c образованием жидкой смеси в модели, помещают жидкую смесь в поры песка и микротрещины модели с использованием анизотропной теории Гассманна и калибруют параметры в модели с использованием измеренных данных.
2. Способ по п.1, в котором добавляют поры глины, поры песка и микротрещины к модели с использованием схемы дифференциальной эффективной среды.
3. Способ по п.2, в котором схема дифференциальной эффективной среды упрощена использованием схемы анизотропной сухой породы.
4. Способ по п.1, в котором разделяют объем пор модели в соответствии с оцененными глинистостью и эффективным напряжением.
5. Способ по п.1, в котором выбирают упомянутые математические отношения следующим образом: часть fClay объема fT пор модели, которая является порами глины, задается как fClay=VshfT; часть fSand, которая является порами песка, задается как ![]() часть fCrack, которая является микротрещинами, задается как
часть fCrack, которая является микротрещинами, задается как ![]() и часть
и часть ![]() которая является порами песка со случайным распределением ориентации, задается как
которая является порами песка со случайным распределением ориентации, задается как ![]() где Vsh - глинистость, нормализованная матрицей зерна,
где Vsh - глинистость, нормализованная матрицей зерна, ![]() fInit - начальная пористость трещин при нулевом давлении вышележащей породы s0 и b - градиент давления в подземной области.
fInit - начальная пористость трещин при нулевом давлении вышележащей породы s0 и b - градиент давления в подземной области.
6. Способ по п.1, в котором данные калибровки содержат лабораторные измерения или каротажные диаграммы.
7. Способ по п.1, в котором первый закон смешивания является средним значением по Фойгту-Рейссу-Хиллу.
8. Способ по п.1, в котором второй закон смешивания является моделью суспензии Вуда.
9. Способ по п.1, в котором вода, используемая для формирования жидкой смеси, дополнительно содержит соль, растворенную в ней.
10. Способ по п.2, в котором схема дифференциальной эффективной среды содержит поры, имеющие предпочтительное распределение ориентации.
11. Способ по п.10, в котором схема дифференциальной эффективной среды сформулирована в терминах следующего дифференциального уравнения:
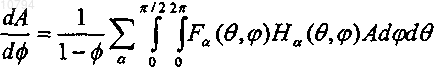
где a - коэффициент сжатия, Fa(q,j) - функция плотности вероятности для распределения ориентации пор и трещин, q и j - соответственно, полярный угол и азимут, А - тензор податливости эффективной среды (с порами) и f - пористость;
![]()
и
![]()
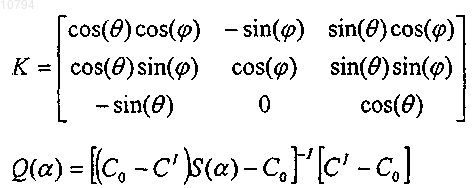
где тензор Q вычислен в местной системе координат, C0 - тензор коэффициентов упругости для модели без пор, C1 - тензор коэффициентов упругости для упомянутой жидкой смеси и S - тензор Эшелби, который является функцией коэффициента сжатия.
12. Способ по п.11, в котором дополнительно выполняют приближение анизотропной сухой породы, полагая
![]()
где A0 - тензор податливости модели без пор, и
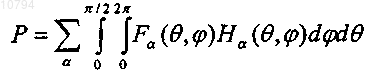
13. Способ по п.2, в котором модель имеет несколько типов пор и различные типы пор добавляются к модели пропорционально, а не последовательно.
14. Способ по п.13, в котором при пропорциональном добавлении нескольких типов пор вычисляют тензор эффективной упругой податливости для модели с порами глины, вычисляют тензор эффективной упругой податливости для модели со всеми порами, включающими смоченные поры глины и сухие поры песка, и микротрещинами, выполняют анизотропную замену текучей среды путем помещения жидкой смеси в поры песка и микротрещины с использованием анизотропной модели Гассманна при использовании тензоров эффективной упругой податливости из предыдущих этапов.
15. Способ по п.12, в котором дополнительно выполняют разложение тензора (1-f)P в степенной ряд.
16. Способ по п.15, в котором разложение в степенной ряд представляет собой
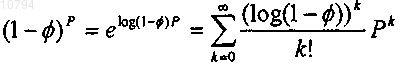
17. Способ по п.16, в котором дополнительно выполняют замену тензора Р на матрицу размерности 9_9, в которой Р является изоморфным.
18. Способ по п.16, в котором дополнительно выполняют приближение результата посредством усечения степенного ряда после N членов, где N равно по меньшей мере 30.
19. Способ по п.1, в котором дополнительно используют модели для обращения сейсмических данных из подземной области, чтобы получить по меньшей мере одно петрофизическое свойство подземной области.
20. Способ по п.19, в котором по меньшей мере одно петрофизическое свойство включает в себя пористость.
Текст
010794 Область техники, к которой относится изобретение Настоящее изобретение, в общем, относится к области геофизической разведки и, в частности, к петрофизическому моделированию и способам прогнозирования и соотнесения упругих свойств, которые влияют на сейсмические данные и поэтому могут быть выведены из сейсмических данных и петрофизических свойств. В частности, настоящее изобретение является способом построения петрофизической модели подземной области, которая учитывает анизотропию в этой области. Предшествующий уровень техники Петрофизическое моделирование играет решающую роль в обращении и интерпретации сейсмических данных, обеспечивая важную связь между петрофизическими свойствами (например, пористостью,глинистостью, водонасыщенностью и т.д.) и сейсмическими свойствами (например, скоростями продольной и поперечной волн, затуханием и частотным составом). Поэтому чрезвычайно важно построить точную и надежную петрофизическую модель, которая представляет совместное воздействие ключевых определяющих факторов, таких как пористость, геометрия пор, связанность пор, жидкостный тип (или водонасыщенность), содержание глины, минералогия, напряжение, температура и анизотропия. Известно, что осадочные горные породы (тип горных пород, в которых часто может быть найдена нефть) являются анизотропными по природе. Это значит, что их упругие свойства изменяются в зависимости от направления. Недавно изданная литература показывает, что сейсмическая анизотропия является первичным фактором, определяющим зависимость амплитуды отражения от удаления (АОУ). На сейсмограмме общей глубинной точки (ОГТ) амплитуда сейсмического отражения от конкретной границы изменяется в зависимости от удаления и угла падения. Зависимость изменения амплитуды от удаления может быть связана с характером насыщенности горной породы. Например, типичные газоносные песчаные пласты, залегающие под глинистым сланцем, часто характеризуются классом III зависимости амплитуды отражения от удаления, то есть отрицательной полярностью на границе и увеличением амплитуды с удалением. Нефтеносные песчаные пласты могут показывать класс II зависимости амплитуды отражения от удаления, то есть очень слабую амплитуду при небольшом удалении и сильную амплитуду при большом удалении. Авторы настоящего изобретения обнаружили, что эффект анизотропии особенно важен для песчаных пластов с высоким импедансом (акустический импеданс песчаных пластов выше,чем акустический импеданс окружающего их глинистого сланца). Фиг. 1 показывает коэффициент отражения продольной волны от одиночной границы как функцию от угла падения с использованием как изотропной 11, так и анизотропной 12 модели геологической среды. Она ясно демонстрирует, что анизотропия является важным фактором для моделирования зависимости амплитуды отражения от удаления. Это особенно верно для углов падения больше 30. Результаты также демонстрируют, что очень желательна теоретическая петрофизическая модель с анизотропными характеристиками. Существуют два важных типа анизотропии в обломочных осадочных горных породах: анизотропия глинистых сланцев и анизотропия, обусловленная напряжением. Анизотропия глинистых сланцев является обычной в обломочных горных породах. Анизотропия глинистых сланцев является наиболее обычной анизотропией в осадочной горной породе просто потому, что более 70% осадочных горных пород являются глинистыми сланцами. Анизотропия глинистых сланцев обусловлена предпочтительной ориентацией пространства пор между частицами глины. Обусловленная напряжением анизотропия вызвана неравномерными напряжениями в земной коре. Вообще говоря, три основных напряжения часто отличаются друг от друга вследствие тектонического движения земной коры и влияния вышележащих пород. В типичном ненапряженном осадочном бассейне, предполагающем незначительное тектоническое движение, вертикальное напряжение часто намного выше, чем два горизонтальных напряжения. В направлении главного основного напряжения горная порода сжата больше по сравнению со сжатием в двух других направлениях. Это неравномерное уплотнение приведет к неравномерному замыканию мягких пор или трещин в горной породе. Трещины, выровненные перпендикулярно к главному основному напряжению, имеют более высокую тенденцию быть закрытыми, чем трещины, выровненные в других направлениях. Следовательно, продольная волна будет перемещаться быстрее в направлении главного основного напряжения. Как правило, анизотропия глинистых сланцев является сильной (выше 10%). Сейсмическая анизотропия обычно измеряется с использованием параметров Томсена (Thomsen) ,и , которые определены следующим образом: Здесь Cij - тензор упругости анизотропной горной породы. Величинаявляется приблизительной-1 010794 мерой анизотропии продольной волны, то есть относительным изменением между скоростью продольной волны в быстром направлении и в медленном направлении. Аналогично величинаслужит мерой анизотропии поперечной волны. Величиназадает распределение скоростей продольной волны и вертикально поляризованной волны сдвига при промежуточных углах между быстрым и медленным направлениями. Как правило,илииспользуется для количественного выражения сейсмической анизотропии. Таким образом, определение характеристики анизотропии в 20% означает, что скорость продольной или поперечной волны в быстром направлении приблизительно на 20% быстрее, чем в медленном направлении. Поскольку анизотропия глинистых сланцев является сильной, она имеет больший эффект на моделирование зависимости амплитуды отражения от удаления, чем анизотропия, обусловленная напряжением. Обусловленная напряжением анизотропия обычно наблюдается в неглубоко залегающих рыхлых песчаных пластах, в которых вертикальное эффективное напряжение может быть значительно выше, чем горизонтальные эффективные напряжения. В случаях, когда есть небольшое тектоническое движение,анизотропия, обусловленная напряжением, не может быть измерена с использованием каротажа со скрещенными диполями, поскольку два горизонтальных напряжения являются приблизительно одинаковыми. В областях, где тектоническое движение является большим, существует азимутальная анизотропия, и она может быть измерена с использованием каротажа со скрещенными диполями. В отличие от анизотропии глинистых сланцев, анизотропию, обусловленную напряжением, более сложно прогнозировать,так как основные напряжения определяются многими факторами, в том числе вышележащей породой,тектоникой, локальными структурами, системами разломов и свойствами горной породы. Различные теории, называемые теориями эффективной среды, были предложены для моделирования анизотропии глинистых сланцев или анизотропии, обусловленной напряжением, в горных породах. Некоторые из них кратко рассмотрены ниже. Большинство этих теорий игнорирует механическое взаимодействие между порами/трещинами. Поэтому эти теории эффективной среды действительны только для слабой концентрации пор. Это ограничение делает теории первого порядка малопригодными на практике. Проблема может быть решена использованием схемы дифференциальной эффективной среды (ДЭС) или самосогласованной схемы. Схема дифференциальной эффективной среды рассмотрена Nishizawa,Journal of Physical Earth 30, 331-347 (1982) и Hornby, et al. in Geophysics 59, 1570-1583 (1994). Самосогласованная (SC) схема рассмотрена Hill, Journal of Mechanics and Physics of Solids 13, 213-222 (1965) иWillis, J. Mech. Phys. Solids 25, 185-202 (1977). Однако каждая из этих схем очень сильно замедляет числовые расчеты. Было бы желательно ускорить вычисления, сохраняя точность способа. Кроме того, не существует модели, которая одновременно может оперировать как анизотропией глинистых сланцев, так и анизотропией, обусловленной напряжением. Настоящее изобретение удовлетворяет обеим этим потребностям. Эмпирические петрофизические модели широко используются в промышленности вследствие своей простоты. Эти эмпирические модели обычно предполагают линейные отношения между скоростью продольной волны (или поперечной волны), пористостью и/или глинистостью. Несмотря на некоторый ограниченный успех таких моделей, имеются растущие проблемы с их применимостью для обращения сейсмических данных (то есть для нахождения петрофизических свойств с использованием сейсмических данных), поскольку они определяются данными. Без большого количества данных для их калибровки эти эмпирические модели часто дают неправильные, а иногда даже вводящие в заблуждение результаты. Во многих обстоятельствах исследования и/или разработки часто нет данных, необходимых для калибровки. Другой важный недостаток эмпирических моделей состоит в том, что они дают плохое физическое представление. Например, можно найти простые отношения между проницаемостью и скоростью и заключить, что проницаемость является главным определяющим фактором для скорости, тогда как фактически изменение скорости в значительной степени обусловлено пористостью. Хорошая корреляция между пористостью и проницаемостью делает проницаемость похожей на определяющий фактор для скорости. Проницаемость имеет значение, но обычно оказывает на скорость вторичный эффект. Наконец,эмпирическая модель может иметь дело лишь с очень ограниченным количеством факторов, обычно меньше трех. Для всестороннего петрофизического моделирования нужно учитывать совокупный эффект пористости, типа пор, глинистости, содержания текучей среды (водонасыщенности), движения текучей среды, давления, температуры и частоты. В литературе имеется ограниченное количество теоретических петрофизических моделей. Например, М.А. Biot, "Theory of propagation of elastic waves in a fluid saturated porous solid", Journal of Acousticwaves in two-phase media, Parti: Theoretical formulation", Geophysics 39, 537-606 (1974). Вообще говоря,эти модели могут быть использованы для объяснения упругости, наблюдаемой в лаборатории. Однако часто трудно применить эти модели к реальным случаям (например, каротажным диаграммам). Сю (Xu) и Уайт (White) разработали практическую модель, которая воспроизводит совокупный эффект множества факторов на скорости продольной и поперечной волн ("A new velocity model for clay-sand mixtures",Geophysical Prospecting 43, 91-118 (1995) и "А physical model for shear-wave velocity prediction", GeophysicalProspecting 44, 687-717 (1996. Но эта модель не оперирует эффектом анизотропии. Хорнби (Hornby) и др.-2 010794 предлагают модель эффективной среды для моделирования анизотропии глинистых сланцев (Geophysics 59, 1570-1583 (1994. Но их модель ограничена только чистыми глинистыми сланцами и не применима к песчанистым сланцам или глинистым песчаникам. Это очень ограничивает применимость их модели,поскольку осадочные породы состоят не только из глинистых сланцев, но также и других типов пород,таких как песчаник, алеврит, известняк и т.д. Кроме того, подход Хорнби действителен только для высоких частот и поэтому всегда не согласуется с теорией Гассманна (Gassmann). Теория Гассманна получила широкое применение в нефтедобывающей промышленности для замены текучей среды (гипотетической замены текучей среды в порах коллекторной породы с одного типа на другой, например воды на нефть). Одно ключевое предположение в теории Гассманна состоит в том, что частота сейсмической волны является достаточно низкой, чтобы давление поры имело достаточное время для установления равновесия. Поэтому любую модель, которая дает чувствительность на низких частотах или выровненное давление в порах, называют согласуемой с теорией Гассманна. Кейз (Keys) и Сю (Xu) (Geophysics 67, 1406-1414 (2002 предлагают способ приближения сухой породы, который намного ускоряет числовые расчеты схемы дифференциальной эффективной среды,поддерживая ее точность. К сожалению, предложенный способ не работает для анизотропного случая. Замена текучей среды является важной темой для сейсмической идентификации пластовой жидкости. Традиционно различные жидкие фазы, например газ и водный раствор солей, смешивают с использованием закона суспензии Вуда (Wood) перед их помещением в горную породу с использованием уравнения Гассманна (1951). Этот подход помещает жидкие смеси однородно во все пространство пор независимо от размера пор, смачиваемости и проницаемости горной породы. Лабораторные измерения демонстрируют, что подход, вероятно, применим к горным породам с относительно высокой проницаемостью и при относительно высоких эффективных напряжениях, когда микротрещины закрыты. Очень сомнительно, что этот подход применим к глинистым пескам, в которых микропоры имеют тенденцию быть смоченными водой вследствие капиллярного эффекта. Таким образом, имеется потребность разработки анизотропной петрофизической модели, которая имеет фундаментальное физическое обоснование. Модель должна быть согласуемой с теорией Гассманна и правильно трактовать капиллярный эффект при различном распределении жидкой фазы по размеру пор. Модель должна быть достаточно точной и эффективной для применения к анализу каротажных диаграмм и/или обращения сейсмических данных. В частности, модель должна иметь возможность оперировать различными видами анизотропии (например, анизотропией глинистых сланцев и анизотропией, обусловленной напряжением). Настоящее изобретение удовлетворяет эту потребность. Сущность изобретения Согласно изобретению создан способ создания анизотропной петрофизической вычислительной модели подземной области, моделирующей анизотропию глинистых сланцев и анизотропию, обусловленную напряжением, и имеющей объем пор, глинистость и объем песка, в котором измеряют давление вышележащей породы и глинистости в подземной области, разделяют объем пор модели на поры глины,поры песка и микротрещины, выбирают математические отношения, при которых разделение объема пор на три части может быть выполнено количественно на основе оценок давления вышележащей породы и глинистости в подземной области, смешивают песчаные зерна с частицами глины в модели с использованием первого закона смешивания, добавляют смоченные поры глины с предпочтительным распределением ориентации к относящейся к глине части объема пор модели, добавляют пустые поры песка и выровненные микротрещины, соответственно, к частям песка и микротрещин объема пор модели, смешивают углеводороды с водой с использованием второго закона смешивания с образованием жидкой смеси в модели, помещают жидкую смесь в поры песка и микротрещины модели с использованием анизотропной теории Гассманна и калибруют параметры в модели с использованием измеренных данных. В способе можно добавлять поры глины, поры песка и микротрещины к модели с использованием схемы дифференциальной эффективной среды. Указанная схема может быть упрощена использованием схемы анизотропной сухой породы. В способе можно разделять объем пор модели в соответствии с оцененными глинистостью и эффективным напряжением. При осуществлении способа можно выбирать упомянутые математические отношения следующим образом: часть Clay объема T пор модели, которая является порами глины, задается как Clay=VshT; часть часть Crack, которая являетсяSand, которая является порами песка, задается как микротрещинами, задается как которая является порами песка со где Vsh - глинистость, норInit - начальная пористость трещин при нулемализованная матрицей зерна,вом давлении вышележащей породы 0 и- градиент давления в подземной области. Данные калибровки могут содержать лабораторные измерения или каротажные диаграммы. Первый закон смешивания может быть средним значением по Фойгту-Рейссу-Хиллу. Второй закон-3 010794 смешивания может быть моделью суспензии Вуда. Вода, используемая для формирования жидкой смеси, может дополнительно содержать соль, растворенную в ней. Схема дифференциальной эффективной среды может содержать поры, имеющие предпочтительное распределение ориентации, и может быть сформулирована в терминах следующего дифференциального уравнения: где- коэффициент сжатия, F(,) - функция плотности вероятности для распределения ориентации пор и трещин,и- соответственно, полярный угол и азимут, А - тензор податливости эффективной среды (с порами) и- пористость; и где тензор Q вычислен в местной системе координат, C0 - тензор коэффициентов упругости для модели без пор, C1 - тензор коэффициентов упругости для упомянутой жидкой смеси и S - тензор Эшелби, который является функцией коэффициента сжатия. В способе можно дополнительно выполнять приближение анизотропной сухой породы, полагая где A0 - тензор податливости модели без пор, и Модель может иметь несколько типов пор, и различные типы пор добавляются к модели пропорционально, а не последовательно. При пропорциональном добавлении нескольких типов пор можно вычислять тензор эффективной упругой податливости для модели с порами глины, вычисляют тензор эффективной упругой податливости для модели со всеми порами, включающими смоченные поры глины и сухие поры песка и микротрещинами, выполняют анизотропную замену текучей среды путем помещения жидкой смеси в поры песка и микротрещины с использованием анизотропной модели Гассманна при использовании тензоров эффективной упругой податливости из предыдущих этапов. В способе можно дополнительно осуществлять разложение тензора (1-)P в степенной ряд, которое может представлять собой Можно дополнительно осуществлять замену тензора Р на матрицу размерности 99, в которой Р является изоморфным. В способе может дополнительно выполнять приближение результата посредством усечения степенного ряда после N членов, где N равно по меньшей мере 30. В способе можно дополнительно использовать модель для обращения сейсмических данных из подземной области, чтобы получить по меньшей мере одно петрофизическое свойство подземной области,которое может включать в себя пористость. Краткое описание чертежей Настоящее изобретение и его преимущества будут более понятны при обращении к последующему подробному описанию и приложенным чертежам, на которых изображено следующее: фиг. 1 изображает график, иллюстрирующий воздействие анизотропии горной породы на коэффициент отражения горной породы; фиг. 2 - блок-схему последовательности операций, показывающую основные этапы способа одного варианта воплощения настоящего изобретения; фиг. 3 - схематическую диаграмму, дополнительно иллюстрирующую блок-схему последовательности операций, представленную на фиг. 2; фиг. 4 - блок-схему последовательности операций схемы дифференциальной эффективной среды,-4 010794 измененной в настоящем изобретении для пропорционального добавления различных типов пор к модели во время построения модели; фиг. 5 А-5 Е иллюстрируют воздействие обусловленной напряжением анизотропии на прогнозирование поперечной волны и плотности; фиг. 6 А-6 С иллюстрируют воздействие анизотропии на привязку каротажных данных к сейсмическим данным (фиг. 6 А 1 является копией фиг. 6 А). Изобретение будет описано в связи с его предпочтительными вариантами воплощения. Однако в тех случаях, когда последующее подробное описание является специфичным для конкретного варианта воплощения или конкретного использования изобретения, предполагается, что оно является только иллюстративным и не должно рассматриваться как ограничение объема изобретения. Напротив, предполагается, что оно охватывает все альтернативы, модификации и эквиваленты, которые могут быть включены в сущность и объем изобретения, определенные в соответствии с приложенной формулой изобретения. Подробное описание предпочтительных вариантов воплощения Настоящее изобретение обеспечивает интегрированную анизотропную петрофизическую модель,которая моделирует как анизотропию глинистых сланцев, так и обусловленную напряжением анизотропию обломочных горных пород. Модель также учитывает совокупное воздействие пористости, глинистости, водонасыщенности, давления, температуры и движения текучей среды в порах на скорости продольной и поперечной волн согласованным образом. В модели, как обобщено в уравнении (1), общий объем пор разделен на три части в соответствии с оцененными глинистостью и эффективным напряжением: поры глины, поры песка и микротрещины (главным образом, в песчаном компоненте). Модель воспроизводит анизотропию глинистых сланцев через предпочтительную ориентацию пор глины (Clay), а обусловленную напряжением анизотропию - через предпочтительную ориентацию микротрещин (Crack), которые определяются неравномерными напряжениями. Необходимы лабораторные измерения или каротажные данные, чтобы установить отношение между плотностью трещин и эффективным напряжением. Пространство пор разделено на поры глины и поры песка с использованием схемы, которую предложили Сю (Xu) и Уайт(White): где Vsh - глинистость, нормализованная матрицей зерна. Предполагается, что анизотропия в глинистых сланцах обусловлена предпочтительным распределением ориентации пор глины, которое может быть описано, например, с помощью Гауссовского распределения. Поры песка далее разделяются на два типа: которая имеет случайное распределение ориентации, и микротрещины первичная пористостьCrack, которые имеют предпочтительное распределение ориентации. Предполагается, что первичная пористость песка не зависит от напряжения. Но распределение ориентации микротрещин и пористость трещин определяются тремя основными напряжениями. В ненапряженных геологических условиях, например, вертикальное напряжение обычно выше, чем два горизонтальных напряжения. В этом конкретном случае микротрещины имеют тенденцию ориентироваться вертикально. В результате скорость продольной волны имеет тенденцию быть выше в вертикальном направлении, чем в двух горизонтальных направлениях. Лабораторные измерения демонстрируют, что пористость трещин может быть связана с давлением вышележащей породы с использованием эмпирического отношения. Например,где Init - начальная пористость трещин при нулевом давлении вышележащей породы 0 и- градиент давления. Наконец, первичная пористость песка со случайной ориентацией пор может быть записана как Коротко говоря, модель воспроизводит анизотропию глинистых сланцев через предпочтительную ориентацию пор глины, а обусловленную напряжением анизотропию - через предпочтительную ориентацию микротрещин, которые определяются неравномерными напряжениями. Лабораторные измерения или каротажные данные могут использоваться, чтобы установить отношения между плотностью трещин и эффективным напряжением. Фиг. 2 является блок-схемой последовательности операций, показывающей, как модель работает. Модель более наглядно проиллюстрирована с помощью схематической диаграммы на фиг. 3. На этапе 21 песчаные зерна смешиваются с частицами глины с использованием закона смешивания (например, среднего значения Фойгта-Рейсса-Хилла (Voigt-Reuss-Hill). На этапе 22 поры глины добавляются к матрице с использованием схемы дифференциальной эффективной среды (ДЭС) или схемы приближения анизо-5 010794 тропной сухой породы (ПАСП), которые будут описаны позже, чтобы учесть механическое взаимодействие между порами. Предполагается, что добавленные поры глины всегда являются смоченными водой вследствие капиллярного эффекта (см. описание ниже). На этапе 23 первичные поры песка и микротрещины добавляются к системе аналогичным образом, за исключением того, что здесь к системе не добавляется текучая среда в этих порах или трещинах. На этапе 24 углеводороды смешиваются с водным раствором солей/водой с использованием закона смешивания, такого как модель суспензии Вуда (Wood).al., Stanford University (1996); среднее значение Фойгта-Рейсса-Хилла описывается на стр. 127 той же книги.) Затем на этапе 25 используется анизотропная модель Гассманна для помещения жидкой смеси в порах песка (включая микротрещины) в систему. (См. Brown and Korringa, "On the dependence of elasticproperties of a porous rock on the compressibility of the pore fluid, Geophysics 40, 608-616 (1975).) Затем могут быть вычислены скорости продольной и поперечной волн и параметры Томсена (этап 26 на фиг. 3) из эффективных коэффициентов упругости, которые могут быть получены с использованием модели породы, созданной в соответствии с вышеописанными процедурами. Дополнительными признаками, представленными на фиг. 3, является разделение объема поры модели на часть 31, содержащую заполненные жидкостью (водным раствором солей) поры 32 глины, часть 33, содержащую пустые поры 34 песка, и часть 35, содержащую пустые микротрещины 36. Различные признаки способа изобретения, представленного на фиг. 2 и 3, далее будут рассмотрены дополнительно. Влияние микропористости на распределение жидкой фазы и замена текучей среды Способ настоящего изобретения рассматривает микропористость и распределение текучей среды в масштабе пор иначе, нежели это делают традиционные подходы. Традиционные модели замены текучей среды Гассманна предполагают однородно смешанные жидкие фазы и помещают жидкую смесь в пространство пор независимо от размеров пор. С другой стороны, анизотропная модель микропористости настоящего изобретения предполагает, что микропоры, или поры глины, имеют тенденцию быть занятыми водной фазой вследствие их меньшего размера по сравнению с порами песка. Это справедливо, главным образом, потому, что капиллярное давление в порах глины значительно ниже, чем капиллярное давление в порах песка. Эта концепция реализуется посредством добавления пор глины с водным раствором солей/водой (этап 22) к системе. Можно ожидать, что это даст чувствительность на высокой частоте для пор глины с точки зрения механизмов потока жидкости, так как все теории дифференциальной эффективной среды (ДЭС) предполагают изолированное пространство пор. Однако поры песка (в том числе трещины) рассматриваются по-другому. Как указано выше, они сначала добавляются к системе, и затем используются анизотропные уравнения Гассманна для помещения жидкой смеси в пустые поры/трещины. Поскольку теории Гассманна предполагают выровненное давление в порах среди пор песка, можно ожидать, что это даст чувствительность на низкой частоте для пор песка. Анизотропной замене текучей среды Гассманна нужен тензор податливости твердой матрицы в качестве входных параметров. Для традиционной замены текучей среды Гассманна это просто. Однако в способе настоящего изобретения это более сложно, так как замена текучей среды выполняется только для пор песка в предположении, что поры глины смочены водой. В этом случае поры глины рассматриваются как часть "твердой матрицы," и тензор податливости эквивалентной "твердой матрицы", которая содержит все поры глины, вычисляется с использованием теории дифференциальной эффективной среды или способа анизотропного приближения сухой породы, которые будут описаны ниже. Вычисленный тензор податливости затем используется для анизотропной замены текучей среды Гассманна. Теория дифференциальной эффективной среды (ДЭС) Нисизава (Nishizawa) показал, как вычислить тензор эффективных коэффициентов упругости для твердого тела, заполненного параллельными порамиPhysical Earth 30, 331-347 (1982. Настоящее изобретение расширяет теорию Нисизавы на случай, когда поры могут иметь предпочтительное распределение ориентации, и формулируют дифференциальные уравнения в подходе, предложенном Хорнби и др. где- коэффициент сжатия. F(,) - функция плотности вероятности для распределения ориентации пор/трещин ии- соответственно, полярный угол и азимут. Таким образом, Далее, А - тензор податливости эффективной среды, который нужно определить, и- пористость: и, наконец, Тензор Q вычислен в локальной системе координат, где ее ось z выбрана параллельной оси симметрии включения. Здесь C0 и C1 - тензоры коэффициентов упругости, соответственно, твердой и жидкой фаз. S - тензор Эшелби (Eshelby) (1957), который является функцией формы поры (коэффициента сжатия) ("The determination of the elastic field of an ellipsoidal inclusion, and related problems", Proceedingsof Royal Society of London, Series A 241, 376-396 (1957. Тензор S может быть вычислен с использованием уравнений, заданных Эшелби, когда твердое тело основы является изотропным, и заданных авторами Лин (Lin) и Мура (Mura), когда твердое тело основы является поперечно изотропным (Lin, S. and Mura,Т., Phys. Status Solidi, (a)15, 281-285 (1973. Способ приближения анизотропной сухой породы (ADA) Теория дифференциальной эффективной среды, описанная выше, дает довольно точные результаты,но она является затратной в вычислительном отношении. Чтобы улучшить эффективность кода, настоящее изобретение расширяет способ приближения сухой породы, разработанный авторами Кейз (Keys) и Сю (Xu) (2002), на анизотропный случай ("An approximation for the Xu-White velocity model", Geophysics 67, 1406-1414 (2002. Для сухой породы C1=0, и тензор Q 4-ого порядка, определяемый уравнением (11),может быть записан как Здесь I - тензор идентичности. Ключевая идея заключается в том, что тензор S является приблизительно независимым от пористости в сухой породе и поэтому остается постоянным. В этом случае дифференциальное уравнение (5) может быть записано как Решение дифференциального уравнения дает где A0 - тензор податливости твердой матрицы, А - тензор податливости эффективной среды. Следует отметить, что Р является тензором 4-го порядка, а не скаляром. Приближение анизотропной сухой породы намного увеличивает скорость вычисления. Реализация теории дифференциальной эффективной среды в пористом соединении с множественными группами пор В системе с одной группой пор реализация схемы дифференциальной эффективной среды является простой. См. Хорнби и др. или О. Nishizawa, "Seismic velocity anisotropy in a medium containing orientedcracks - Transversely isotropic case", Journal of Physical Earth, 30, 331-347 (1982). В системе с несколькими типами пор различные типы пор обычно добавляются к системе с последовательным использованием схемы дифференциальной эффективной среды (например, Сю и Уайт, 1995). Таким образом, этапы 22-24 на фиг. 2 могут использовать схему дифференциальной эффективной среды, вместо схемы приближения анизотропной сухой породы. Теория дифференциальной эффективной среды реализована таким образом,чтобы сделать легче последующую замену текучей среды Гассманна. Однако это делает результирующий тензор эффективной упругой податливости асимметричным, то есть результирующий тензор эффективной упругой податливости зависит от порядка, в котором добавляются поры. Предположим, что имеется бимодальное распределение податливых и жестких пор. Результат, полученный добавлением снача-7 010794 ла податливых пор, будет отличаться от результата, полученного добавлением сначала жестких пор. Чтобы решить эту проблему, настоящее изобретение раскрывает другую схему для реализации теории дифференциальной эффективной среды. В этой схеме все типы пор добавляются пропорционально на каждой итерации. (Схема дифференциальной эффективной среды делит общую пористость на N групп. Число N может быть, например, равно 50 или 100 в зависимости от отношения пористости к коэффициенту сжатия. Затем схема дифференциальной эффективной среды последовательно (одну за другой) добавляет группы пор к системе. На отдельной стадии, когда группа пор добавляется к системе, результирующая эффективная среда в предыдущей стадии используется как среда основы для этой новой стадии. Каждая стадия названа выше итерацией, поскольку коэффициенты упругости матрицы обновляются на каждой итерации.) Используется процедура с тремя этапами, как проиллюстрировано на блок-схеме последовательности операций, представленной на фиг. 4. На этапе 41 вычисляется только тензор эффективной упругой податливости для твердого тела с порами глины (смоченными водой). На этапе 42 вычисляется тензор эффективной упругой податливости для твердого тела со всеми порами (смоченными водой для пор глины и сухими для пор песка и трещин). На этапе 43 выполняется замена анизотропной жидкой среды с использованием вычисленных выше тензоров упругой податливости. Реализация модели с приближением анизотропной сухой породы Тензор податливости А в уравнении (13) является центральной частью приближения анизотропной сухой породы. Тензор (1-)P в уравнении (13) может быть определен посредством разложения в степенной ряд: Тензор Р в уравнении (14) изоморфен матрице с размерностью 99. То есть существует взаимнооднозначное преобразование из пространства тензоров четвертого ранга в пространство матриц с размерностью 99, которое сохраняет умножение и сложение. Следовательно, тензор Р в уравнении (14) может быть заменен матрицей Р с размерностью 99, с тем чтобы степенной ряд в уравнении (14) определялся обычными матричными операциями. Оценка для приближения сухой породы может быть получена посредством усечения ряда (14) после достаточного количества членов. Вычислительное испытание показывает, что уравнение (14) дает точные результаты, если ряд усекается после 30 членов. Примеры Способ настоящего изобретения был применен к анализу каротажных данных и сейсмическому моделированию, и наблюдались существенные улучшения в предсказании поперечной волны и привязке каротажных данных к сейсмическим данным. Фиг. 5 В-Е сравнивают диаграммы измеренной (более темная кривая) поперечной волны 52 (фиг. 5 В) и плотности 54 (фиг. 5 С) с расчетами (53, 55) с использованием традиционной изотропной петрофизической модели. Можно наблюдать устойчивое отклонение между измерениями и расчетами на интервалах 51 песка, соответствующих низким значениям Vsh доли глинистости, которая показана как функция от глубины на фиг. 5 А. Это было интерпретировано как эффект вызванной напряжением анизотропии в рыхлых песках. Фиг. 5D (поперечная волна) и 5 Е (плотность) показывают, что способ настоящего изобретения намного улучшает согласованность между расчетными результатами 57, 59 и измеренными данными 52, 54 в интервалах 51 песка. Более подробно диаграммы поперечной волны и плотности могут быть спрогнозированы на основе диаграммы Р-волны (не показана) и глинистости (показана на фиг. 5 А) с использованием способа обращения, который предложили Сю (Xu) и Уайт (White) (Geophysical Prospecting 44, 687-717 (1996. Кроме того, требуются также упругие свойства и плотность текучих сред в порах, которые могут быть вычислены с использованием корреляций, которые опубликовали Базтл (Baztle) и Ванг (Wang) (Geophysics 57,1396-1408 (1992. Чтобы сделать прогноз, также нужны еще два параметра для изотропной петрофизической модели. Это коэффициенты сжатия, соответственно, для пор песка и пор глины. Для анизотропной петрофизической модели нужны четыре дополнительных параметра. Это коэффициент сжатия для микротрещин, стандартное отклонение для распределения ориентации для пор глины (предполагая Гауссовское распределение), стандартное отклонение для распределения ориентации для микротрещин (снова предполагая Гауссовское распределение) и плотность трещин. Плотность трещин может быть вычислена с использованием уравнения (3). Эти параметры могут быть откалиброваны с использованием лабораторных измерений и/или каротажных данных (например, диаграмм каротажа S-волны со скрещенными диполями). Фиг. 6 А-С показывают влияние анизотропии (как вызванной напряжением, так и глинистых сланцев) на сейсмическое моделирование. Сейсмограмма в скважине показана на фиг. 6 А (фиг. 6 А 1 является копией фиг. 6 А). Фиг. 6 В показывает синтетическую сейсмограмму, формированную с помощью традиционной изотропной модели геологической среды. Фиг. 6 С показывает синтетическую сейсмограмму,формированную с помощью анизотропной модели геологической среды настоящего изобретения. Очевидно, анизотропная модель геологической среды значительно улучшает привязку каротажных данных к сейсмическим данным на большом удалении. Более подробно, чтобы судить, является ли привязка каро-8 010794 тажных данных к сейсмическим данным хорошей или плохой, нужно сравнить синтетическую сейсмограмму с сейсмограммой в скважине. Сравнивая синтетическую сейсмограмму, сформированную на основе изотропной модели геологической обстановки (фиг. 6 В) с сейсмограммой в скважине (фиг. 6 А),можно видеть хорошее согласование при малых удалениях (первые 10-20 трасс). Но сейсмические отклики при больших удалениях (последние 10-20 трасс) выглядят совсем по-разному. Поэтому нужно определить привязку каротажных данных к сейсмическим данным для изотропной модели геологической среды как плохую. При сравнении фиг. 6 С с фиг. 6 А имеется хорошее согласование на всех смещениях. Поэтому привязка каротажных данных к сейсмическим данным для анизотропной модели геологической среды является очень хорошей. Результат указывает, что анизотропия является первичным фактором для сейсмического моделирования в этом случае. Предшествующая заявка направлена на конкретные варианты воплощения настоящего изобретения с целью его иллюстрирования. Однако специалисту в области техники будет очевидно, что возможны многие модификации и разновидности вариантов воплощения, описанных здесь. Подразумевается, что все такие модификации и разновидности содержатся в объеме настоящего изобретения, определенного в приложенной формуле изобретения. ФОРМУЛА ИЗОБРЕТЕНИЯ 1. Способ создания анизотропной петрофизической вычислительной модели подземной области,моделирующей анизотропию глинистых сланцев и анизотропию, обусловленную напряжением, и имеющей объем пор, глинистость и объем песка, в котором измеряют давление вышележащей породы и глинистости в подземной области, разделяют объем пор модели на поры глины, поры песка и микротрещины, выбирают математические отношения, при которых разделение объема пор на три части может быть выполнено количественно на основе оценок давления вышележащей породы и глинистости в подземной области, смешивают песчаные зерна с частицами глины в модели с использованием первого закона смешивания, добавляют смоченные поры глины с предпочтительным распределением ориентации к относящейся к глине части объема пор модели, добавляют пустые поры песка и выровненные микротрещины,соответственно, к частям песка и микротрещин объема пор модели, смешивают углеводороды с водой с использованием второго закона смешивания c образованием жидкой смеси в модели, помещают жидкую смесь в поры песка и микротрещины модели с использованием анизотропной теории Гассманна и калибруют параметры в модели с использованием измеренных данных. 2. Способ по п.1, в котором добавляют поры глины, поры песка и микротрещины к модели с использованием схемы дифференциальной эффективной среды. 3. Способ по п.2, в котором схема дифференциальной эффективной среды упрощена использованием схемы анизотропной сухой породы. 4. Способ по п.1, в котором разделяют объем пор модели в соответствии с оцененными глинистостью и эффективным напряжением. 5. Способ по п.1, в котором выбирают упомянутые математические отношения следующим образом: часть Clay объема T пор модели, которая является порами глины, задается как Clay=VshT; часть часть Crack, которая являетсяSand, которая является порами песка, задается как микротрещинами, задается как которая является порами песка со где Vsh - глинистость, нор мализованная матрицей зерна,Init - начальная пористость трещин при нулевом давлении вышележащей породы 0 и- градиент давления в подземной области. 6. Способ по п.1, в котором данные калибровки содержат лабораторные измерения или каротажные диаграммы. 7. Способ по п.1, в котором первый закон смешивания является средним значением по ФойгтуРейссу-Хиллу. 8. Способ по п.1, в котором второй закон смешивания является моделью суспензии Вуда. 9. Способ по п.1, в котором вода, используемая для формирования жидкой смеси, дополнительно содержит соль, растворенную в ней. 10. Способ по п.2, в котором схема дифференциальной эффективной среды содержит поры, имеющие предпочтительное распределение ориентации. 11. Способ по п.10, в котором схема дифференциальной эффективной среды сформулирована в терминах следующего дифференциального уравнения: где- коэффициент сжатия, F(,) - функция плотности вероятности для распределения ориентации-9 010794 пор и трещин,и- соответственно, полярный угол и азимут, А - тензор податливости эффективной среды (с порами) и- пористость; и где тензор Q вычислен в местной системе координат, C0 - тензор коэффициентов упругости для модели без пор, C1 - тензор коэффициентов упругости для упомянутой жидкой смеси и S - тензор Эшелби, который является функцией коэффициента сжатия. 12. Способ по п.11, в котором дополнительно выполняют приближение анизотропной сухой породы, полагая где A0 - тензор податливости модели без пор, и 13. Способ по п.2, в котором модель имеет несколько типов пор и различные типы пор добавляются к модели пропорционально, а не последовательно. 14. Способ по п.13, в котором при пропорциональном добавлении нескольких типов пор вычисляют тензор эффективной упругой податливости для модели с порами глины, вычисляют тензор эффективной упругой податливости для модели со всеми порами, включающими смоченные поры глины и сухие поры песка, и микротрещинами, выполняют анизотропную замену текучей среды путем помещения жидкой смеси в поры песка и микротрещины с использованием анизотропной модели Гассманна при использовании тензоров эффективной упругой податливости из предыдущих этапов. 15. Способ по п.12, в котором дополнительно выполняют разложение тензора (1-)P в степенной ряд. 16. Способ по п.15, в котором разложение в степенной ряд представляет собой 17. Способ по п.16, в котором дополнительно выполняют замену тензора Р на матрицу размерности 99, в которой Р является изоморфным. 18. Способ по п.16, в котором дополнительно выполняют приближение результата посредством усечения степенного ряда после N членов, где N равно по меньшей мере 30. 19. Способ по п.1, в котором дополнительно используют модели для обращения сейсмических данных из подземной области, чтобы получить по меньшей мере одно петрофизическое свойство подземной области. 20. Способ по п.19, в котором по меньшей мере одно петрофизическое свойство включает в себя пористость.
МПК / Метки
МПК: G06G 7/48
Метки: области, способ, петрофизической, подземной, создания, модели, анизотропной, вычислительной
Код ссылки
<a href="https://eas.patents.su/15-10794-sposob-sozdaniya-anizotropnojj-petrofizicheskojj-vychislitelnojj-modeli-podzemnojj-oblasti.html" rel="bookmark" title="База патентов Евразийского Союза">Способ создания анизотропной петрофизической вычислительной модели подземной области</a>
Предыдущий патент: Композиция молекулярного сита ssz-61 и его синтез
Следующий патент: Способ осуществления алкилирования
Случайный патент: Многоконтурный реактор для полимеризации олефинов












